Matematika i filozofi. Koliko su matematički dokazi zaista egzaktni. Razumljivost

Koliko filozofi uopće mogu razumjeti što se događa u svijetu kojim danas upravljaju računala ako ne studiraju filozofiju matematike? Razumiju li matematičari čime se uopće bave ako si ne postavljaju filozofska pitanja o svojoj disciplini. U prikazu Predavanja iz filozofije matematike Joela Hamkinsa Željko Ivanković skreće pažnju na pitanja o matematici koja se uobičajeno zapostavljaju

• Naslovna ilustracija: Joel David Hamkins, oxfordski matematičar, logičar i filozof, iz jednog od predavanja dostupnih na Youtube platformi

Filozofiju matematike u Hrvatskoj mogu slušati samo studenti Filozofskog fakulteta u Rijeci*. Ponuđena je kao izborni predmet, no teško je, na temelju informacija na internetskoj stranici Fakulteta, ustanoviti na kojoj je razini studija bila izvođena i kad (ako ikad). Nije vidljiva na internetskim stranicama ni na jednom zagrebačkom studiju filozofije (Filozofski fakultet, Hrvatski studiji, Filozofski fakultet Družbe Isusove), ni u Splitu, Zadru ni u Osijeku. Možda nema zainteresiranih i specijaliziranih nastavnika, možda za temu nisu zainteresirani ni studenti, ili joj nisu dorasli. Ili su posrijedi neke druge okolnosti. Ali zašto nema kolegija filozofije matematike u Hrvatskoj ovdje nije tema, nego zašto bi ga trebalo biti. Nekolicina razloga uočava se već nakon kratkog i površnog razmišljanja.

• I Razlozi

Prvi je taj što je – sve od Talesa, Pitagorejaca, Platona i Aristotela, zatim mislilaca modernog doba Descartesa, Humea, Leibnitza i Kanta – jedan od najznačajnijih poticaja za razvoj filozofije dolazio iz rasprava o prirodi matematike i nekim matematičkim problemima (npr. problem indukcije). I veliki dio suvremene filozofije zaokupljen je odnosom logike, matematike i prirodnih znanosti. Wittgenstein je jedan od najutjecajnijih filozofa 20. stoljeća, a sam je svoj najvažniji doprinos vidio u filozofiji matematike koja je petnaestak godina (od 1929 do 1944)^[i] okupirala njegov interes. (Koliko je važan matematičarima i u matematici, pitanja su za posebne rasprave.) Donekle se studentima filozofija matematike zacijelo predstavlja u ‘rasutom obliku’, proučavanjem antičke, moderne i suvremene filozofije. Je li to dovoljno? Je li dovoljno studente filozofije podsjetiti na natpis na vratima Platonove Akademije  da ‘ne ulazi tko ne zna geometriju’, kao na neki kuriozum iz opće kulture. Uoga matematike u cijeloj povijesti filozofije čini se prvim dovoljnim razlogom za specijalizirani kolegij.

Drugi mi se razlog čini najvažnijim: koliko filozofija može razumjeti današnji svijet a da ne razumije matematiku i njezinu ulogu u suvremenosti? Računalna znanost je matematički projekt, a ona danas organizira život. Bez razumijevanja matematike, filozofska analiza što se tu zbiva nužno je ograničena. Kritike dominacije kvantitativnog u odnosu na kvalitativni pristup u znanosti, posebno društvenoj, zatim kritike kvantifikacije (financijalizacije) svakidašnjeg života, poslovanja i upravljanja državom, nemaju potrebnu uvjerljvost bez objašnjenja u čemu je problem s kvantifikacijom (ako ga ima), te uloge matematike u znanosti i suvremenom načinu života. Bez filozofije matematike u pitanju je ambicija filozofije  da, slijedom hegelijanske tradicije, bude ‘svoje vrijeme mislima obuhvaćeno’.

Treći razlog mogao bi biti specifičan način mišljenja u matematici. Simboličko mišljenje i zaključivanje u nizu koraka zahtijevaju svojevrsnu disciplinu i koncentraciju. Riječ disciplina  određuje područje (trčanje, skakanje uvis, biologija, književnost…), ali ima i druga značenja: disciplinirano učenje uključuje ponavljanje procesa dok se ne usvoji i stekne rutina; disciplina također podrazumijeva strogo slijeđenje pravila i oslonac na formu. Pretraga internetskih stranica potvrdila je da studenti filozofije slušaju (i valjda polažu) elementarnu logiku. Ipak, pitanje je je li upoznavanje s logikom dovoljno za usvajanje discipline mišljenja (ako je se uopće smatra poželjnom). Strogost u izvedbi matematičkih zaključaka korisna je praksa. Dodatno, filozofija matematike paradoksima uvjerljivo ilustrira i svojevrsne granice logičkog pristupa. Što se tiče koncentracije u slijeđenju ideje, koja se u internetsko doba navodno sve više gubi, bez nje nisu razumljivi ni neki tekstovi iz estetike, etike, filozofije politike, i drugih područja. Ipak, simbolički jezik matematike zahtijeva dodatni misaoni napor, stalno vraćanje na značenje i definiciju pojma i izvedbu konzekvenci u novom kontekstu.

Četvrti je razlog tzv. ‘diskurs’, pojam koji se češće koristi nego što se konkretizira. Ako se njime ne opisuju samo komunikacijske razlike među sredinama i socijalnim grupama, onda bi filozofima uz spomenuto stjecanje specifične discipline u mišljenju korisna mogla biti i usporedba matematičkog (racionalističkog) diskursa, raširenog u suvremenom dobu (kao što se primjećuje u drugom razlogu za izučavanje filozofije matematike), s diskursima u kojima je matematički pristup slabiji.

• II Predavanja

Povod za kratku pretragu internetskih stranica hrvatskih studija filozofije knjiga je Joela Davida Hamkinsa Lectures on the Philosophy of Mathematics (Predavanja iz filozofije matematike) koju je MIT Press objavio 2020. godine. Zbog pandemije covid-19 Hamkins je osam predavanja, koja slijede osam poglavlja knjige, studentima Sveučilišta Oxford održao online, a sad su dostupna na Youtube. Počevši od prvog What is number? predavanja se, kao tv-serija, automatski pokreću kad prethodno završi. Prema opisu kolegija od studenata se očekuje da su prije slušali kolegije iz Rane moderne filozofije ili kolegij Znanje i realnost, zatim Logiku i filozofiju jezika i/ili neke kolegije iz filozofije znanosti. Slični se kolegiji mogu naći na hrvatskim filozofskim fakultetima.

Hamkinsova se knjiga ne može čitati a njegova predavanja ne mogu slijediti bez solidnog predznanja iz matematike, ali ne takvog koje je dostižno samo studentima matematike. Uostalom, već na početku prvog predavanja Hamkins napominje da bi dokaz da drugi korijen iz 2 nije racionalan broj morao biti dio opće kulture i morao bi ga se moći sjetiti svatko tko se smatra obrazovanim. Također, neke važne Hamkinsove teme, poput Turingovog stroja i problema zaustavljanja te Goedelovih teorema nepotpunosti, česte su na stranicama za popularizaciju matematike kao što je Cantor’s Paradise i vrlo prisutne u obrazovanoj javnosti (iako je upitno koliko se razumije njihovo značenje).

Hamkins je, kaže za sebe, oboje – matematičar i filozof (također je i profesor logike). Problemima iz filozofije matematike pristupio je „onako kako se organski pojavljuju u matematici“. Zato je, kaže, knjigu organizirao slijedeći matematičke teme, a ne iz filozofske perspektive kako se filozofija matematike obično prikazuje. Ta je razlika vidljiva već u naslovima poglavlja. Kod Hamkinsa, nakon prvog, o brojevima (prirodnim, prostim, cijelim, racionalnim, realnim, transcendentalnim, kompleksnim) sljedećih sedam poglavlja je naslovljeno: 2. Rigor (poglavlje se nastavlja na prvo, otvara se problemom neprekinutosti, a opservira filozofska pitanja koja se pojavljuju uz infinitezimalni račun, limese, derivacije i integrale); 3. Infinity (problem beskonačnosti na matematički način); 4. Geometry (uzor matematičke dedukcije); 5. Proof (što je dokaz i njegovo značenje u matematici); 6. Computability (Izračunljivost, Turing); 7. Incompleteness (Goedel, čiji teorem nepotpunosti u Hamkinsovoj formulaciji glasi da “nijedan konzistentan formalni sustav ne može dokazati svoju konzistentnost”). 8. Set theory (nastojanje da se cijela matemtatika utemelji u teoriji skupova kao svojevrsnoj metafizici matematike).

U preglednim studijama i zbornicima iz filozofije matematike naslovi poglavlja su uglavnom drukčiji. Često započinju pitanjem o realnosti predmeta matematičkog izučavanja, brojeva i oblika (krug, trokut, piramida…), te raspravljaju različite odgovore: platonizam/realizam; naturalizam/empirizam, strukturalizam, fikcionalizam, logicizam, formalizam, konstruktivizam, intuicionizam. To su naslovi sekcija u članku Filozofija matematike u Enciklopediji filozofije Sveučilišta Stanford, kao i poglavlja u Elsevierovom zborniku iz filozofije matematike.

Kad doktorirate matematiku odvedu vas u stražnju sobu u kojoj vam objasne da nije samo i imaginarni broj, svi su brojevi imaginarni, čak i realni. Kate Owens

Ta shvaćanja diskutira i Hamkins, ali u matematičkom kontekstu. Već u prvom poglavlju prikazuje logicizam i strukturalizam, u drugom fikcionalizam, a kasnije i konstruktivizam, formalizam, kako mu se uklope u matematičke teme. Naravno, nije obradio sva pitanja iz filozofije matematike, posebno ne epistemičku perspektivu. Fali mi šira i eksplicitna rasprava radi li se u matematici o otkriću ili stvaranju. Neizbježno spominje paradokse, od Zenona do Russella, ali o inkonzistentnoj matematici čitatelja i studente tek informira. Čak i površni poznavatelji suvremene matematike uočit će da se Hamkins ne bavi filozofijom vjerojatnosti, ni teorijom igara, topologije nema ni u indeksu pojmova, spominje se tek usput itd. Ovo nije kritika nego opis. Navedena tri novija matematička područja spominjem jer je i historijski razvitak matematike jedan od filozofskih problema. Uostalom, literatura na koju upućuje vjerojatno ne ispušta nijedno značajno pitanje. Gotovo uzgred, u kratkom paragrafu u poglavlju o dokazu, spominje “nevjerojatni paralelizam moralnosti i matematike” koji u knjizi Morality and Mathematics iz 2020. istražuje njegov oxfordski kolega Justin Clarke-Doane:

„Na iznenađujućem broju filozofskih fronti dva područja se suočavaju sa zajedničkim problemima i analognim rješenjima i pobijanjima, bilo da je pitanje realizam, a priori potvrda (justification), objektivnost, naturalizam ili pluralizam.“

• III Dokaz

To je doista iznenađenje. Jedno tako ambivalentno područje kao što je moralnost, u kojem se ništa ne može dokazati, dijeli karakteristike s jednim tako egzaktnim područjem kao što je matematika. A možda i nije iznenađenje. “Pritisnuti (da daju) preciznu definiciju, mnogi matematičari bi mogli imati teškoće egzakno reći što je dokaz”, piše Hamkins, koji je u vrijeme objave Predavanja također objavio i dvije knjige o dokazu u matematici^[ii]. “U matematičkoj praksi”, nastavlja, “dokaz je bilo koji zadovoljavajuće detaljan uvjerljivi matematički argument koji logički uspostavlja zaključak teorema iz njegovih premisa.”^[iii] „Zadovoljavajuće detaljan, uvjerljiv“. Prilično neodređeno, kao rukavica u lice filozofima^[iv].

Poglavlje o dokazu nekako završava tradicionalne probleme filozofije matematike, kao što su priroda brojeva, beskonačnost, neprekinutost i dedukcija u geometriji, a otvara se prema novim temama – izračunljivost (posebno zanimljivo pitanje u doba računala), nepotpunost formalnih sustava i teorija skupova. I samo je nekako podijeljeno u dva dijela. U drugom je dijelu definicija formalnog dokaza u matematici:

„Dokaz tvrdnje φ na temelju teorije T u danom sustavu formalnog dokaza, slijed je ili uređeni (ordered) sustav tvrdnji u formalnom jeziku, od kojih je svaka ili logički aksiom, aksiom iz teorije T, ili izvediva iz prethodnih tvrdnji u dokazu pomoću dopuštenih pravila zaključivanja i gdje je finalna tvrdnja φ dokazani teorem. Kad postoji takav dokaz za φ, pišemo T ⊢ φ, i kažemo T dokazuje φ.“^[v]

U drugom se dijelu bavi formalnim dokazom, teorijom dokaza i njihovim formalnim karakteristikama: verifikabilnost, kompletnost, konzistentnost, korektnost (soundness); kompaktnost (finiteness). Tu raspravlja i o neoklasičnoj logici. Formalni dokaz predmet je istraživanja stotinjak godina kao dio nastojanja potpune aksiomatizacije matematike. Prema Davidu Hilbertu dokaz mora postati predmet matematičkog istraživanja

„kao što astronom uzima u obzir promjenu svoje pozicije, fizičar studira teoriju svojeg uređaja, a filozof kritizira razum“^[vi].

Prema tome, dokaz je takva temeljna sastavnica matematike, opis čijih karakteristika bitno karakterizira samu disciplinu, matematiku.

• IV Značenje

Karakteristike formalnog dokaza iz drugog dijela poglavlja o dokazu nužne su za razumijevanje suvremene matematike, no da se iole detaljnije prikažu to bi bio mali studij. U dodatku na kraju prikaza u par se paragrafa elementarno opisuju dileme iz prvog dijela poglavlja: istina i dokaz; razumijevanje i dokaz; objašnjenje i dokaz, egzaktnost dokaza.

Matematičke se tvrdnje uglavnom mogu dokazati na više načina. Dokazi slikom izgledaju neupitni. Zajedno s euklidskom geometrijom, uzimani su kao egzemplar egzaktnog deduktivnog dokaza sve do modernog doba i afirmacije algebre, iako ima bezbroj primjera kad se slikom vara^[vii]. Neki put slika ipak dobro posluži za postavljanje temeljnih matematičkih pitanja.

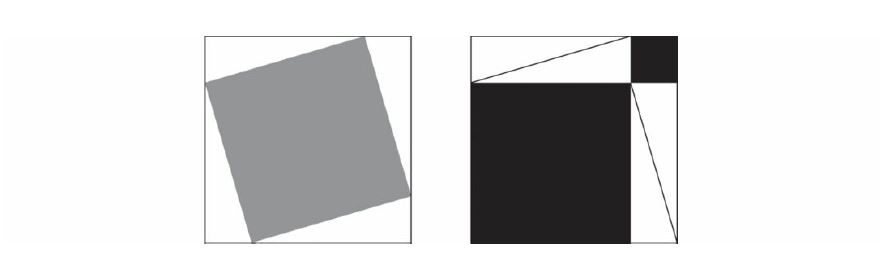
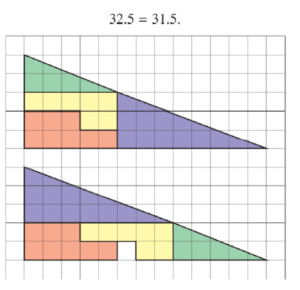
Na gornjoj slici su kvadrati iznad kateta i hipotenuze pravokutnog trokuta^[viii]. Na doljnjoj slici su dva jednaka kvadrata, prvi izveden nakolo kvadrata iznad hipotenuze, a drugi naokolo kvadrata iznad kateta[ix]. Odbiju li se od tih kvadrata četiri jednaka trokuta vidi se da su kvadrat iznad hipotenuze i zbroj kvadrata iznad kateta jednaki. U ovom slučaju se ne radi o optičkoj prijevari (kao u bilješci viii). No, postoji metafizički problem. Na početku je spomenut dokaz da je korijen iz dva iracionalan broj. To znači da se hipotenuza pravokutnog istokračnog trokuta ne može izmjeriti istom mjerom kao i katete. Slično Newtonovom zaključku da je ‘knjiga prirode ispisana jezikom matematike’, u pitagorejskoj je metafizici svijet konstruiran od brojeva i njihovih odnosa[x]. Kad je Hippasus iz Mesponta, otkrio da je korijen iz dva iracionalan broj, da se hipotenuza istokračnog pravokutnog trokuta čiji su kraci dužine 1, ne može prikazati kao omjer, i tako srušio pitagorejsku sliku svijeta, ostali pripadnici te škole/religije/kulta, kojoj je i sam pripadao, navodno su ga – utopili. Dokazi imaju metafizički aspekt. Osim toga, ovime se još jednom, na specifičan način, diskutira priroda brojeva. Iracionalni brojevi izvedeni su (konstruirani su) iz racionalnih, prethodno iz prirodnih, pozitivnih, cijelih. Često se citira zaključak matematičara Leopolda Kroneckera da je „bog stvorio cijele brojeve, sve ostalo je napravio čovjek“. Poglavlje o brojevima Hamlin završava citatom Kate Owens da vas

„kad doktorirate matematiku odvedu u specijalnu sobu i objasne da i nije jedini imaginarni broj – ispada da su svi brojevi imaginarni, čak i realni“.

Sljedeći problem koji proistječe iz ovog primjera je – očiglednost. Dokaz mora biti doveden do razine kad je neupitan, očit da bi ga prihvatili i sumnjivci, a i njegov autor. Ponekad su očitost i formalna egzaktnost dokaza u koliziji. Čuveni je primjer teorem da se svaka mapa može oslikati s četiri boje. Nakon stoljetnih pokušaja dokazan je jednim dijelom i računalom. Dokaz ima 700 stranica i teško da ga itko može provjeriti, a postoji mogućnost da u računalnom programu postoji bug. Ako netko i ima toliko koncentracije opet bi mu drugi morali vjerovati. Tom Leighton navodi primjer doktorske disertacije u kojoj je Gauss spomenuo tvrdnju koju „nitko ne dovodi u pitanje“, no 120 godina poslije je srušena. Također spominje i procjenu prema kojoj je trećina dokaza u matematičkim člancima pogrešna^[xi]. Hamkins navodi primjere nekolicine suvremenih matematičara čije su dokaze preuzimali respektirani kolege a da bi tek oni sami otkrili pogreške u svojim dokazima, ponekad i desetljećima kasnije.

Unatoč spomenutim ograničenjima dokaz računalom  u matematici ipak stječe popularnost. Hamkins (pozivajući se na Thurstona^[xii]) piše da su standardi izrade računalnih programa viši nego u izvedbi formalnog matematičkog dokaza, a ipak imaju bugove. Uobičajeno očekivanje o nepogrešivosti matematičkog dokaza je iluzorno, no nepogrešiva formalna izvedba i nije suština matematičkog dokaza nego – matematička ideja, tvrdi Hamkins. Često su pogrešni dokazi donosili nove ideje. U jednom istraživanju Mike Shulman otkrio je niz pogrešaka u dokazima, ali tvrdi da one nisu bile uočene zato što su u biti sadržavale korektne ideje, koje su u matematici važnije nego precizno formalizirani dokazi. Prema Hamkinsu, samo formalni dokaz bez riječi koje opisuju njegovo značenje, što dokaz objašnjava, što se njime može razumjeti nema zadovoljavajuću težinu. (Malo više o tome u dodatku). Kao da sami matematičari degradiraju egzaktnost koja je u popularnoj predodžbi glavna karakteristika i njihove discipline i njihovog načina razmišljanja

• V Zaključak

Filozofija matematike prije svega razmrdava uobičajene predodžbe o matematici, uz ostalo i predodžbu da je njezina egzaknost neupitna. Ne radi se čak ni samo o tome da i matematičari griješe (očito obilno), nego i o pitanjima o pretpostavkama i pravilima zaključivanja, o tome što se matematikom objašnjava, što njome možemo razumjeti koje je njezino značenje. Onome tko ima strast prema misaonom istraživanju to bi moralo biti intrigantno. Uzmu li se u obzir razlozi na početku članka čini se da bi filozofija matematike morala naći mjesto na studiju filozofije. Udžbenika ne nedostaje, Hamkinsov je jedan od onih za preporučiti. Doduše, studenti filozofije bi morali ‘zagrijati stolicu’ i naučiti nešto matematike. Druga je tema zašto na studiju Matematike nema kolegija Filozofija matematike (osim katkada na doktorskom studiju). Naravno da se matematikom, kao i fizikom, kao i biologijom, može sasvim solidno baviti bez filozofiranja o tim disciplinama. Ipak, kao što se i iz ovog članka vidi, neki matematičari i danas iskoračuju i u filozofiranje o svojoj disciplini, u čemu očito nalaze poticaj i za vlastiti akademski napredak. Po mojem sudu u suradnji s filozofima ta bi aktivnost mogla biti i produktivnija, a u svakom slučaju i jasnija (očiglednija) i razgovjetnija, što nije beznačajno čak ni u matematici[xiii].

 *Zahvaljujem profesorima Majdi Trobok i Zvonimiru Šikiću na korekcijama, uputama i komentarima prve verzije članka.

• Dodatak

U ovom su dodatku neznatno detaljnije prikazane neke dileme iz poglavlja o dokazu: istina i dokaz; razumijevanje i dokaz; objašnjenje i dokaz, egzaktnost dokaza.

Dokaz i istina. Prvo predavanje kolegija Matematika za računalnu znanost na MIT-u Tom Leighton započinje pitanjem: „Tko mi može reći što je dokaz?“ Za razliku od matematičkog dokaza, za koji vrijedi neki formalni opis sličan prije spomenutima, Leighton kaže da je u općem smislu riječi, širem od matematike „dokaz metoda utvrđivanja istine“. Na početku poglavlja o dokazu Hamkins pak piše: „Uvedimo oštru razliku između dokaza i istine.“ Također postavlja pitanje „je li svaka matematička istina istinita s razlogom kao  što je dokaz“? Naravno, postoje matematičke tvrdnje koje su istinite iako još nisu dokazane, odnosno matematičke tvrdnje koji još nisu opovrgnute ni dokazane, ili se ponuđeni dokazi dovode u pitanje. S druge strane, moguće je u nekom formalnom sustavu izvesti dokaz neke tvrdnje, verificirati ga bez ikakve interpretacije njegova značenja, dakle bez rasprave o njegovoj istinitosti. Dalje: „Fikcionalisti tvrde da su rečenice poput ‘drugi korijen iz dva je iracionalan’, strogo govoreći – lažne (false), jer matematički objekt ‘drugi korijen iz dva’ ne postoji,“ pišu Russell i McEvoy^[xiv]. Jesu li matematičke tvrdnje baš lažne ako ne govore o nepostojećim objektima posebno je pitanje, ali prema ovom viđenju matematika nema veze s istinom kao korespondencijom tvrdnje i stvarnosti.

Dokaz i razumljivost. Jedino u poglavlju o dokazu Hamkins spominje Wittgensteina, na manje od jedne od petstotinjak stranica. Izdvaja Wittgensteinov zahtjev da dokaz bude razumljiv: dokaz se može izgubiti u lošoj notaciji i opskurnoj formalizaciji. Računanje u decimalnom sustavu je matematička invencija, tvrdi Wittgenstein. Zaista, zamislimo izvedbu nekih matematičkih dokaza u sustavu rimskih brojeva. Ako se notacija poboljša da postane shvatljiva time se „proizvede dokaz kojeg tu prije nije bilo“, citira Hamkins. Razumljivost kao karakteristika dokaza očito je tema vrijedna diskusije, a zaključci barem dijelom ovise o tome radi li se u slučaju matematike o otkrićima (istine) ili o stvaranju (kao kad dobra notacija omogući dokaz), dakle o shvaćanju njezine prirode.

Wittgenstein ističe reproducibilnost, još jednu zanimljivu karakteristiku dokaza. Za razliku od Leonardovih slika, matematički smo dokaz u stanju egzaktno reproducirati, krugovi ne moraju biti egzaktno okrugli, linije ne moraju biti egzaktno ravne, to je „prednost dokaza pred slikanjem“, tvrdi Wittgenstein. Dokaz se može reproducirati egzaktno, ponekad čak kraće, elegantnije i jasnije nego u originalnom obliku, kao da je u osnovi riječ o ideji nevezanoj za formu. S druge strane, nije riječ samo o jasnoći i eleganciji: notacija omogućava nove, prije nepostojeće uvide (ideje). U lošoj notaciji ali i lošoj formalizaciji ta ideja nestaje, ne postoji.

Egzaktnost i razumljivost. Uobičajeno se pretpostavlja da je cilj matematičke formalizacije egzaktnost, neporecivost dokaza. Na tom su putu međutim mnoge prepreke. Ista se stvar može formalizirati na niz načina, objašnjava Hamkins. Iako svi mogu biti jednako egzaktni, ne objašnjavaju svi predmet jednako elegantno, jasno i razgovjetno. Iako to matematičaru ne moraju biti unutrašnji kriteriji (za razliku od egzaktnosti) cilj je matematike ipak da nešto objasni. Ako je tome tako elegantnost, jasnost i razumljivost postaju dopuna egzaktnosti.

Dokaz dokazuje, dokaz je dijalog. Catarina Dutilh Novaes (Sveučilište Vrije Amsterdam)

Dokaz i dijalog. Napokon, Hamkins skreće pažnju da je Catarina Dutilh Novaes recentno objavila knjigu^[xv] o fundamentalno dijaloškoj prirodi (deduktivnog) matematičkog dokaza, čak i onog koji matematičar izvodi sam ili, recentno, u ‘komunikaciji’ s računalom.  Novaes navodi šest vrsta dokaza, odnosno šest aspekata dokaza:

1. dokaz kao verifikacija (istinitosti teorema)
2. dokaz kao potvrda (certifikacija); dokaz se mora izložiti sumnjivcima i kad ih dovoljan broj (a što ovisi o kontekstu) potvrdi da nisu našli grešku onda je certificiran; važno je, naravno i jesu li skeptici respektirani matematičari ili recenzenti u opskurnom časopisu; ili laici
3. dokaz kao komunikacija i uvjeravanje
4. dokaz kao objašnjenje ne samo da je nešto istinito nego i zašto je istinito
5. dokaz kao inovacija, kad dokaz ponudi novu ideju ili perspektivu (u nekoliko važnih slučajeva, piše Hamkins, čak je i pogrešan dokaz otvorio novi poged na problem)
6. dokaz kao sistematizacija, kad ujedini ideje koje prije nisu bile prikazane kao povezane

Pogleda li se malo bolje, ovi aspekti atribuiraju matematičkom dokazu upravo karakteristike kao što su razumljivost, objašnjenje, dovode ga o socijalni kontekst i u odnos s istinom.

• Bilješke

^[i] Wittgenstein’s Philosophy of Mathematics, Stanford Encyclopedia of Philosophy

^[ii] Proof and the Art of Mathematics, MIT Press 2020; Proof and the Art of Mathematics: Examples and Extensions, MIT Press 2021

^[iii] Istu je definiciju ponovio i u prvoj od svoje dvije spomenute knjige o dokazu.

^[iv] U članku A History of Mathematical Proof: Ancient Greece to the Computer Age, David C. Bramlett i Carl T. Drake, citiraju drukčiji opis dokaza, također općenit i neodređen:

“Dokaz je stablo tvrdnji (tree of statements), povezano implikacijama, čija je konačna točka zaključak a početna točka su ili podatci ili generalno prihvaćene činjenice ili principi.”

^[v] So, what is proof? A truly robust answer arises with the concept of formal proof provided by mathematical logicians in the subject of proof theory. Let us concentrate on formal proof for the rest of this chapter. Formal proof is exacting and precise, written in a formal language and according to rigid rules concerning the allowed axioms and rules of inference. Namely, a proof of an assertion φ from a theory T in a given formal proof system is a sequence or ordered system of assertions in the formal language, each of which is either a logical axiom, an axiom of T, or deducible from earlier assertions in the proof by an allowed rule of inference, and where the final assertion is φ, the theorem being proved. When there is such a proof of φ, we write T ⊢ φ, pronounced “T proves φ.”

^[vi] Proof Theory, Stanford Encyclopaedia of Philosophy

^[vii] Hamkins navodi ovaj ‘dokaz’ da je 32,5=31,5. Hipotenuza doljnjeg trokuta nije ravna nego slomljena, on je neznatno veći.

^[viii] Slike su prenesene iz knjige John Stillwell: A Concise History of Mathematics for Philosophers, Cambridge University Press 2019

[ix] Otprilike ovako:

[x] Profesorica Trobok me podsjetila da su Grci pod ‘brojevima’ uključivali i ‘formu’ odnosno ‘oblik’

^[xi] Treće predavanje Matematike za računalnu znanost na MIT-u

^[xii] Thurston, William P. 1994. On proof and progress in mathematics. Bulletin of the American Mathematical Society

[xiii] Ovdje želim podsjetiti na slavni primjer Russella i Whitheheada (Principia Mathematica) kojima je trebalo 360 stranica da dokažu da je 1+1=2, što je „možda navelo Russella da napusti jednostavnu interpretaciju logicističkog projekta, prema kojem pouzdano znamo aksiome i izvodimo znanje o teoremima iz tog početnog znanja“ pišu Marcus Russell i Mark McEvoy u Uvodu zbornika  An Historical Introduction to the Philosophy of Mathematics: A Reader Marcus Russell i Mark McEvoy. Bloomsbury Publishing 2016.  Dalje citiraju Russella iz knjige Logički atomizam:

“Kad je čista matematika organizirana kao deduktivni sustav – t.j. kao skup tvrdnji koje mogu biti deducirane iz izabranog skupa premise – postaje očito da, ako je do toga da vjerujemo u istinu čiste matematike, to ne može biti zato što vjerujemo u istinu tog skupa premise. Neke premise su puno manje očite nego neke od njihovih konzekvenci I u njih se vjeruje uglavnom zbog njihovih konzekvenci. To će se uvijek dogoditi kad je znanost organizirana kao deduktivni sustav. Nisu logički najjednostavnije tvrdnje u sustavu najočitije, niti one predstavljaju glavni razlog da vjerujemo u sustav”

^[xiv] Russell i McEvoy. ibid.

^[xv] The Dialogical Roots of Deduction