Bulovska logika pojmova. Forme, strukture i implikacije

U uvodu u bulovsku logiku pojmova, Zvonimir Šikić povezuje pojmovne i egzistencijske forme, uvodi interpretacije kroz B–strukture i objašnjava kako logičke veze među pojmovima zahtijevaju sofisticiranije testove valjanosti nego što ih nudi istinosno–funkcionalna analiza.

1. Operatori na pojmovima

Vennovi dijagrami jasno upućuju na to da se Aristotelovi operatori “svi su”, “nijedan nije”, “neki su” i “neki nisu” mogu definirati pomoću operatora ∃ (postoji) i njegove negacije -∃ (ne postoji). Naime, križić znači da nešto postoji, a iscrtkavanje da nešto ne postoji. Dakle, imamo sljedeće ekvivalencije.

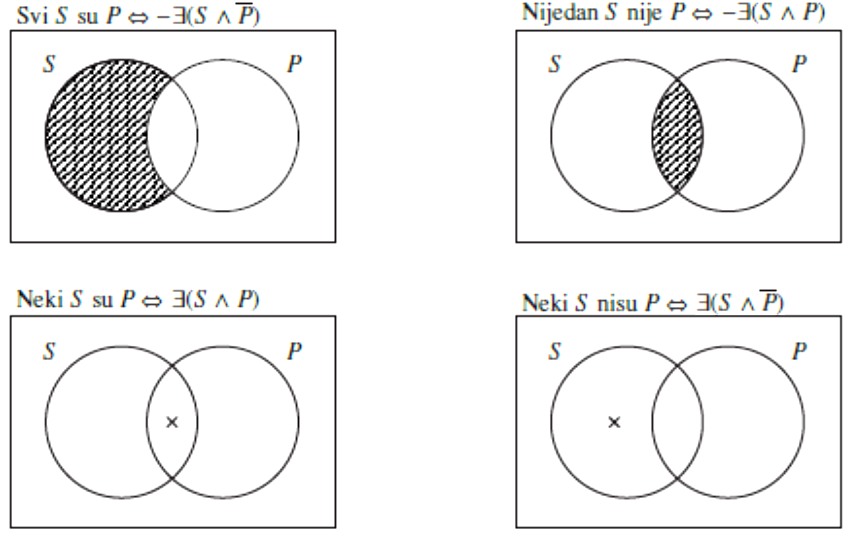
Tvrdnju oblika ∃A, gdje je A složeni pojam izgrađen od jednostavnijih uz pomoću istinosnih funkcija, zovemo egzistencijskom bulovskom tvrdnjom. Njom se tvrdi da postoji x o kojem je A istinito. No, što znači da je A istinito o x, tj. da je A(x), ako je A istinosna funkcija od P,…,S ? Odgovor je jednostavan:

­­

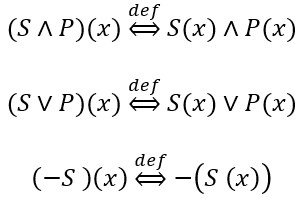
i tako dalje.

Na desnim stranama, koje definiraju lijeve strane, istinosne funkcije imaju svoje standardno značenje. Dakle (kako i treba) pojam “zao ∧ čovjek” obuhvaća sve zle ljude, pojam “-živo” sve nežive stvari, pojam “majka ∨ otac” sve roditelje itd.

Odmah možemo zaključiti da sve IF-ekvivalencije u ovom pojmovnom kontekstu postaju jednakosti ekstenzija odgovarajućih pojmova; A ⇔ B akko A(x) ⇔ B(x), tj. ext(A) = ext(B). Slično, A ⇒ B akko A(x)⇒B(x) tj. ext(A) ⊆ ext(B).

Operator ∃ koristi ćemo kao osnovni operator koji primijenjen na pojam daje tvrdnju. No, osim tim unarnim operatorom koristit ćemo se i operatorom ∀, te binarnim operatorima = i ⊆. Boole je kao osnovni operator koristio =. Sve su to operatori koji primijenjeni na pojmove daju tvrdnje i svi se oni lako definiraju pomoću osnovnog operatora ∃.

­­

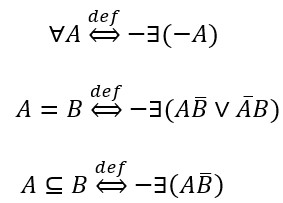
Dakle, kategoričke tvrdnje oblika A, E, I, O možemo izraziti i na sljedeće načine.

­­

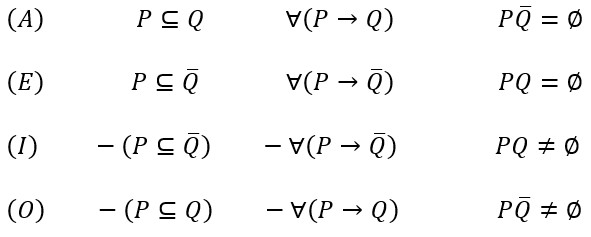
Metodu Vennovih dijagrama, kojom smo rješavali silogističke probleme, možemo primijeniti i na širu klasu problema u kojima se pojavljuju egzistencijske bulovske forme (koje prikazujemo križićima) i njihove negacije (koje prikazujemo iscrtkavanjima). Istražimo, na primjer, koju konkluziju možemo izvesti iz premisa:

(1) Svi P su Q ili R.

(2) Neki P nisu Q.

Preformulirat ćemo ih u egzistencijske forme ili njihove negacije, te ih prikazati odgovarajućim Vennovim dijagramom:

­­

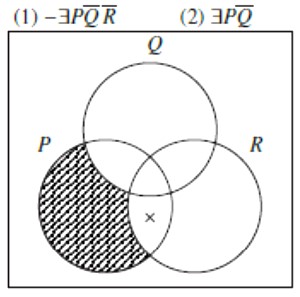
Iz dijagrama možemo iščitati moguću konkluziju \(\small \exists P\overline{Q}R\) ili bliže hrvatskom jeziku: Neki P su R i nisu Q.

Metoda postaje još fleksibilnijom ako uvedemo konvenciju da više crtom povezanih križića u raznim područjima znači da nečega ima bar u jednom od tih područja. Ilustrirat ćemo je izvođenjem konkluzije iz sljedećih premisa:

(3) Svi P koji su Q su R.

(4) Neki P su Q ili R.

Premise ćemo opet preformulirati u egzistencijske forme ili njihove negacije, te ih prikazati sljedećim dijagramom.

­­

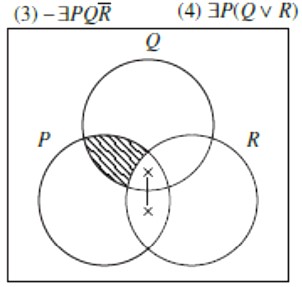
Iz dijagrama odmah iščitavamo moguću konkluziju \(\small \exists PR\) ili bliže hrvatskom jeziku: Neki P su R.

2. Bulovske forme i njihova logika

Metoda Vennovih dijagrama, osim što postaje nepreglednom u slučaju većeg broja atomarnih pojmova, nije primjerena logičkoj analizi tvrdnji koje su od egzistencijskih tvrdnji izgrađene primjenom proizvoljnih IF–veznika (a ne samo primjenom negacije, kao do sada). Takve forme zovu se bulovskim formama.

DEFINICIJA BULOVSKE FORME (B–FORME)

Ako neki skup IF–veznika generira sve IF–veznike, npr. {∧,∨,-}, onda su bulovske forme generirane sljedećim pravilima.

(i) Atomi P, Q, R, P₁, Q₁, R₁,… su pojmovne forme.

(ii) Ako su A i B pojmovne forme onda su to i (A ∧ B), (A ∨ B), (-A).

(iii) Ako je A pojmovna forma onda je ∃A bulovska forma, koju zovemo egzistencijskom.

(iv) Ako su F i G bulovske forme onda su to i (F ∧ G), (F ∨ G), (-F).

Primijetimo da su bulovske forme forme tvrdnji (označavamo ih s F, G, H,… ) dok su pojmovne forme forme pojmova (označavamo ih s A, B, C,… ). Specijalno, atomarne bulovske forme (P, Q, R,… ) su pojmovne. (Sve forme u ovom odjeljku bit će bulovske, pa ćemo često ispuštati termin “bulovski”.)

Definiranje formi je, kao i uvijek, naš prvi korak u izgradnji odgovarajuće logike, u ovom slučaju bulovske logike pojmova. Sljedeći je korak definiranje interpretacija tih formi. Budući da vrijednost istinitosti interpretacije od ∃A ovisi samo o ekstenziji interpretacije od A, te da je ekstenzija interpretacije od A potpuno određena ekstenzijama koje imaju interpretacije onih atoma koji se pojavljuju u A, onda su u bulovskoj logici forme jednoznačno interpretirane ekstenzijama njihovih pojmovnih atoma.

DEFINICIJA INTERPRETACIJE BULOVSKE FORME (B–STRUKTURE)

Interpretacija bulovske forme je pridruženje podskupova nekog nepraznog skupa U atomima te forme. Skup U zovemo univerzumom te interpretacije. To pridruženje može biti totalno ili parcijalno, tj. može pridruživati podskupove od U svim ili samo nekim pojmovnim atomima. Bulovske interpretacije češće se zovu bulovskim strukturama.

Na primjer, sljedeća tablica zadaje B–strukturu čiji je univerzum U = {a, b, c}, a pridruženje podskupova od U atomima P i Q je ext(P) = {a, c} i ext(Q) = {a}.

­­

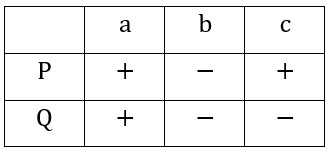
Istu strukturu zadaje i sljedeći dijagram:

­­

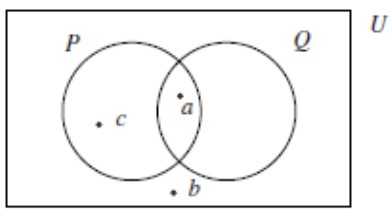
Tako možemo prikazati bilo koju konačnu strukturu, tj. strukturu s konačnim univerzumom U, čija je funkcija ext definirana na konačno mnogo atoma.

Univerzum U ne mora biti konačan i  pridruženje ext ne mora biti definirano samo na konačnom broju atoma. Na primjer, B–struktura u kojoj je U = \(\small \mathbb{N}\) ={0, 1, 2, 3,…} i u kojoj je ext(P_n) = n\(\small \mathbb{N}\) = {0, n, 2n, 3n,…} ima beskonačan univerzum, a pridruženje ext je definirano na beskonačno mnogo atoma P_n.

U prethodnim obrazloženjima pretpostavili smo da je intuitivno jasno kako se izračunavaju vrijednosti istinitosti bulovske forme u zadanoj B–strukturi (tu vrijednost također zovemo interpretacijom te forme u toj strukturi). Na primjer, izračun vrijednosti istinitosti  forme ∃P → -∃(P ∧ Q) u gore zadanoj konačnoj strukturi izgleda ovako:

­­ ­

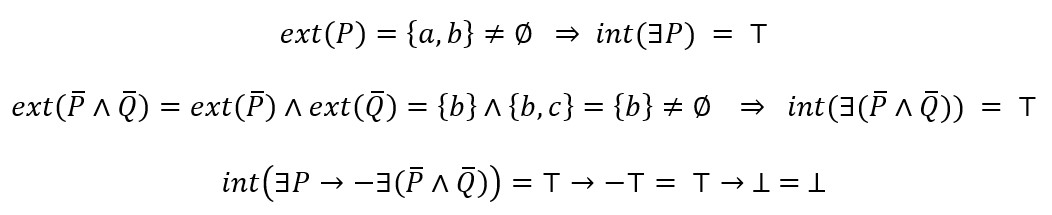
Dakle, interpretacija zadane forme u zadanoj strukturi je ⊥, tj. zadana forma je neistinita u zadanoj B–strukturi. Općenito imamo sljedeću definiciju.

DEFINICIJA ISTINITOSTI BULOVSKE FORME U B–STRUKTURI

Interpretaciju (tj. vrijednost istinitosti) bulovske forme u B–strukturi koja je zadana univerzumom U i  pridruženjem ext koje pridružuje podskupove od U svim atomima te forme, označava se s int i definira se sljedećim pravilima.

(i) Na atomima je ext već definirano.

(ii) ext(A ∧ B) = ext(A) ∧ ext(B), ext(-A) = –ext(A) itd.

(iii) int(∃F) = ⊤ ⇔ ext(F) ≠ ∅

(iv) int(F ∧ G) = int(F) ∧ int(G), int(-F) = –int(F) itd.

Gornja definicija zapravo opisuje kako se funkcija ext, definirana samo na atomima (i), proširuje na sve pojmovne forme (ii), kako se pomoću nje int definira na egzistencijskim formama (iii) te kako se int zatim proširuje na sve forme (iv).

Sljedeći korak u izgradnji bulovske logike je definicija generalizirane implikacije ⊨ među B–formama. On je standardan.

DEFINICIJA BULOVSKE IMPLIKACIJE

Skup bulovskih formi Γ implicira skup bulovskih formi Δ, oznakom Γ ⊨ Δ, ako ne postoji B–struktura u kojoj su sve forme iz Γ istinite i sve forme iz Δ  neistinite, tj. ako su sve forme iz Γ  istinite onda je bar jedna forma iz Δ istinita.

Preostao nam je zadnji korak u našem pristupu izgradnji svih logika: pronalaženje algoritma za testiranje implikacije Γ ⊨ Δ. Čini se da u bulovskoj logici to postaje bitno teže. Naime, čak i za konačne skupove bulovskih formi Γ i Δ broj mogućih interpretacija, tj. B–struktura, beskonačan je (jer je i broj mogućih univerzuma beskonačan). Dakle, za doslovno testiranje implikacije Γ ⊨ Δ  trebalo bi izračunati vrijednosti istinitosti formi iz Γ i Δ u beskonačno mnogo B–struktura. To ne izgleda kao algoritam koji će u konačno mnogo koraka odgovoriti vrijedi li Γ ⊨ Δ.  Ako algoritam uopće postoji, sigurno je sofisticiraniji.

Promotrimo još jednom primjer konkretne implikacije iz uvodnog poglavlja, za koju smo tvrdili da je valjana.

\(
\begin{array}{l}
\text{(7) Ako su svi odbijeni kandidati VKV, onda neki kandidati nisu odbijeni.} \\
\text{(8) Ili su svi kandidati odbijeni ili su svi kandidati VKV.} \\
\hline
\text{(9) Ako su svi VKV kandidati odbijeni onda neki kandidati koji nisu VKV jesu odbijeni.}
\end{array}
\)

Njegova forma očito je sljedećeg oblika:

­­

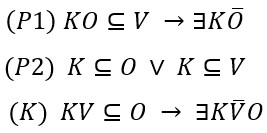
Izrazimo li ⊆ pomoću ∃ dolazimo do istog argumenta iskazanog pomoću bulovskih formi:

­­

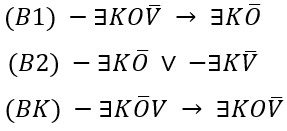
Njezina IF–forma je:

­­

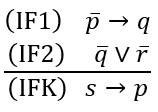
Egzistencijske forme B–zaključka atomarne su forme IF–zaključka (označili smo ih malim slovima p,q i r da ih ne brkamo s pojmovnim atomima). Metodom semantičkih stabala lako možemo ustanoviti da premise (IF1) i (IF2) istinosno-funkcionalno ne impliciraju konkluziju (IFK), tj. da \(\small \overline{p} \rightarrow q, \ \overline{q} \lor \overline{r} \ \not\models\ \overline{s} \rightarrow p\).

­­

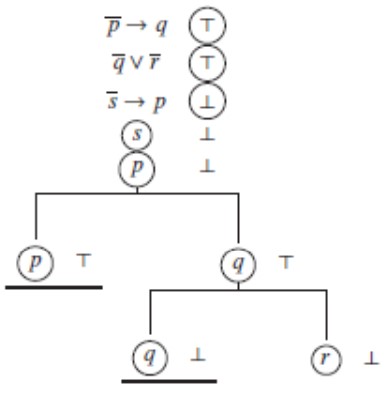
S najdesnije grane možemo iščitati interpretaciju u kojoj su obje premise istinite, a konkluzija je ipak neistinita:

­­

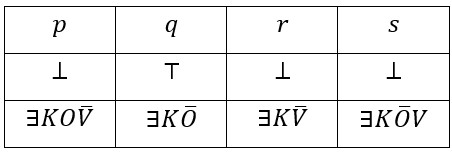
Naravno, u toj IF–analizi nismo uzeli u obzir bulovsku formu od p, q, r i s koja je prikazana u zadnjem redu tablice. Ako i nju uzmemo u obzir onda vidimo da interpretacija (p, q, r, s)=(⊥,⊤,⊥,⊥) nije moguća, što znači da je implikacija ipak bulovski valjana. Naime,\(\small r = \exists K\overline{V} = \bot \ \text{i} \ s = \exists K\overline{O}V = \bot\) u kontradikciji je s \(\small \ q = \exists K\overline{O} = \top\), što dokazujemo sljedećim Vennovim dijagramom.

­­

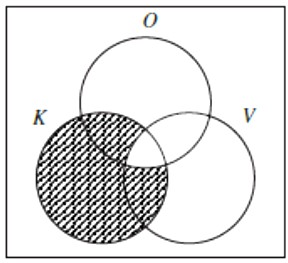
Ako \(\small r = \exists K\overline{V} = \bot \ \text{i} \ s = \exists K\overline{O}V = \bot\), što prikazuju iscrtkavanja, onda je i \(\small \ q = \exists KO = \bot\), jer je područje \(\small K\overline{O}\) iscrtkano. To je u kontradikciji s \(\small \ q = \exists K\overline{O} = \top\).

Egzistencijske forme \(\small \exists K\overline{O}, \ \exists K\overline{V} \ \text{i} \ \exists K\overline{O}V\) ne mogu imati proizvoljne, međusobno neovisne interpretacije i to je bio uzrok neuspjeha naše IF–analize kao dokaza valjanosti implikacije. Međutim, očito je da ćelije \(\small KOV, \ \overline{K}OV, \ K\overline{O}V, \ KO\overline{V}, \ \overline{K}\overline{O}V\),… (na koje K,O i V dijele univerzum U), nešto sadrže ili ne sadrže neovisno jedna o drugoj.

­­

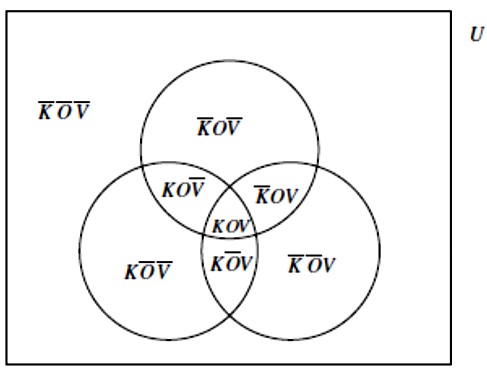
To znači da ćelijske egzistencijske forme \(\small \exists KOV, \ \exists \overline{K}OV, \ \exists K\overline{O}V, \ \exists KO\overline{V}, \ \exists \overline{K}\overline{O}V\)… (u kojima ∃ djeluje na potpune blokove u kojima se pojavljuju svi atomi dane forme) mogu imati proizvoljne međusobno neovisne interpretacije. Slijedi da su sve moguće interpretacije onih bulovskih formi čije su egzistencijske forme ćelijske, ništa drugo do sve moguće IF–interpretacije njenih ćelijskih egzistencijskih formi. Zato se testiranje takvih ćelijskih formi svodi na standardne IF–testove.

Postupak ilustriramo na našem primjeru:

­­

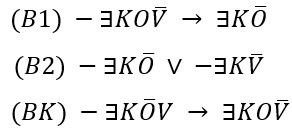
Najprije blokove proširimo do potpunih blokova:

­­

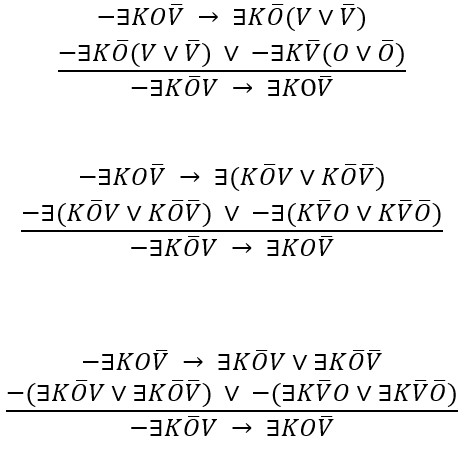
Zatim formuliramo IF- formu tog potpunog argumenta:

­­

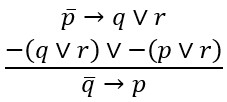
Konačno testiramo taj IF-argument:

­­

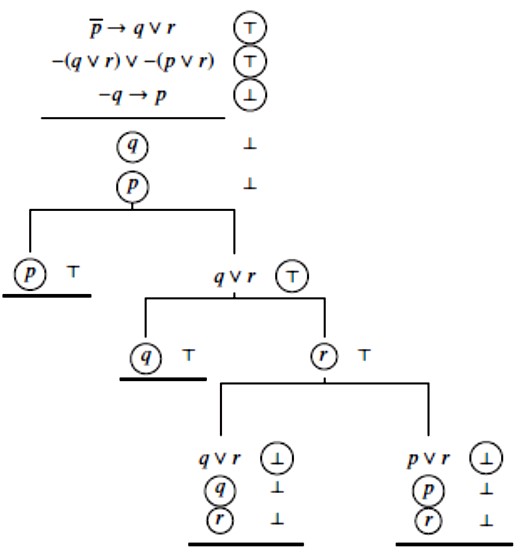
Sve su se grane zatvorile što znači da

­­

No onda i

­­

Ovaj postupak uvijek funkcionira, jer je svaka bulovska forma ekvivalentna ćelijskoj bulovskoj formi (tj. onoj čije su egzistencijske forme ćelijske). Naime, svaka egzistencijska forma ∃A ekvivalentna je ćelijskoj formi ∃(K₁ ∨ … ∨ K_n) koja je očito ekvivalentna s ∃K₁ ∨ … ∨ ∃K_n (nečega ima u uniji svih K_i akko nečega ima u bar jednom K_i). Taj se postupak zove Herbrandova metoda, jer ga je uveo Herbrand 1930.