Elementarno o Einsteinovoj specijalnoj teoriji. Euklidska i hiperbolička geometrija

Potaknut člankom Daria Hrupeca o brzini svjetlosti, Zvonimir Šikić predstavlja jednostavno matematičko objašnjenje zašto je nužno da ona bude jednaka u svim referentnim sustavima, a potom proširuje temu pogledom na malo poznate Epsteinove dijagrame, te ih uspoređuje s dijagramima Hermanna Minkowskog.

• Naslovna fotografija: Njemački teorijski fizičar Albert Einstein (lijevo), njemački matematičar i fizičar Hermann Minkowski (desno). (Creative Commons)

U članku objavljenom u Idejama Dario Hrupec je objasnio zašto je brzina svjetlosti nužno jednaka u svim (inercijalnim) sustavima: budući da nema medija u kojem se val svjetlosti širi, nema ni preferiranog sustava koji bi jednoznačno određivao njegovu brzinu. Zatim je dodao da sve u Einsteinovoj specijalnoj teoriji relativnosti [1] slijedi iz te invarijantnosti. Da je zaista tako pokazujem u 1. poglavlju ovog članka na krajnje elementaran način (odabrani polaznici V. Gimnazije, od 1. do 4. razreda, kojima sam to svojevremeno izložio nisu imali poteškoća da razumiju izlaganje). U 2. poglavlju pokazujem kako se sve to jednostavno geometrizira pomoću Epsteinovih dijagrama [2] koji su, nažalost, gotovo nepoznati. Ta se geometrizacija temelji na euklidskoj (tj. školskoj) geometriji. U 3. zahtjevnijem poglavlju uspoređujem Epsteinove dijagrame s dijagramima Minkowskog [3] koji su dobro poznata geometrizacija specijalne teorije relativnosti koja se bazira na hiperboličkoj geometriji.

• I

Pod pretpostavkom da je brzina svjetlosti u svim (inercijskim) sustavima ista, fenomen desinkronizacije kvalitativno je veoma jednostavan.

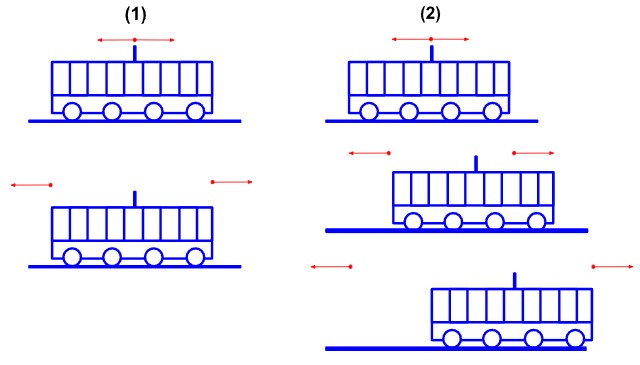
Razmotrimo dva referentna sustava:

(1) sustav vagona (giba se udesno),
(2) sustav tračnica (miruje).

Što se događa kada upalimo svjetlo u sredini vagona?

(1) U sustavu vagona, svjetlo dolazi do „krme“ i „pramca“ vagona istovremeno. Kažemo da su “krmeni događaj” i “pramčani događaj” istovremeni.

(2) U sustavu tračnica brzina svjetlosti je ista u oba smjera pa će se krmeni događaj dogoditi prije pramčanog događaja (jer se krma giba prema svjetlu, a pramac od svjetla).

Ono što je istovremeno u jednom sustavu nije istovremeno u drugom, tj. sustavi imaju različita vremena.

Čak ni kvantitativno objašnjenje desinkronizacije nije naročito teško. (U nastavku pretpostavljamo da su naše osnovne jedinice takve da je brzina svjetlosti c = 1.)

Zamislite vagon kao sat. Njegov osnovni vremenski interval je vrijeme koje svjetlosni signal treba da stigne od dna do vrha vagona. Taj interval u sustavu tračnica označimo s ∆t, a onaj u sustavu vagona s ∆t‘.

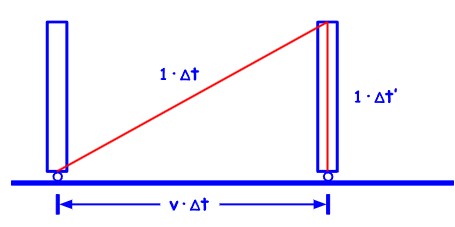
Ako je v brzina vagona u odnosu na tračnice, onda je

­\( v^2 \Delta t^2 + 1^2 (\Delta t’)^2 = 1^2 \Delta t^2 \)

­­\( \Delta t’ = \Delta t \sqrt{1 – \frac{v^2}{1^2}} \)

Vrijeme u sustavu koji se giba kontrahira se za faktor \( \sqrt{1 – \frac{v^2}{1^2}} \) (tj. \( \sqrt{1 – \frac{v^2}{c^2}} \)). Nadalje, brzina vagona u odnosu na tračnice jednaka je brzini tračnica u odnosu na vagon (ako kao pozitivne smjerove od x i x’ uzmemo smjerove kretanja) pa je

­\( \frac{\Delta x}{\Delta t} = v = \frac{\Delta x’}{\Delta t’} \)

­\( \Delta x’ = \Delta x \frac{\Delta t’}{\Delta t} = \Delta x \sqrt{1 – v^2} \)

Duljina u sustavu koji se giba kontrahira se za isti faktor \( \sqrt{1 – \frac{v^2}{1^2}} \) (tj. \( \sqrt{1 – \frac{v^2}{c^2}} \)).

Desinkronizaciju lako možemo objasniti i kvantitativno. U trenutku t=0 (koji je sinkroniziran u oba sustava) palimo svjetlo u sredini vagona. Krmeni događaj k i pramčani događaj p su istovremeni u sustavu vagona, ali u sustavu tračnica događaju se u različitim vremenima, t_k<t_p.

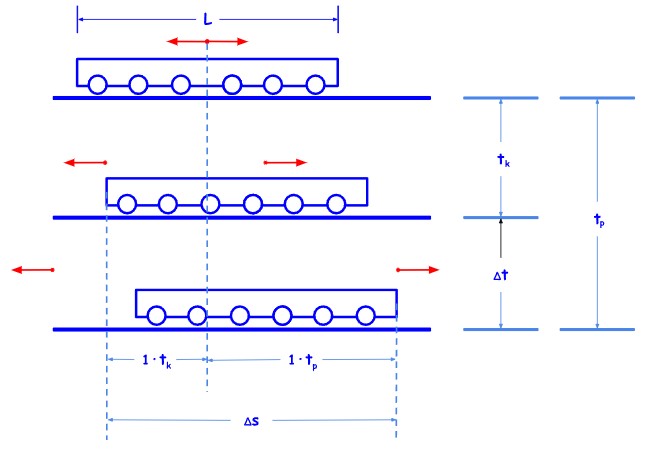
Udaljenost ct_k=1t_k koju vagon prijeđe dok svjetlo dođe do krme jednaka je polovici duljine vlaka, L/2, umanjenoj za udaljenost koju je vlak prešao u vremenu t_k:

­\( 1t_k = \frac{L}{2} – vt_k \)

Slično, udaljenost ct_p=1t_p koju vagon prijeđe dok svjetlo dođe do pramca jednaka je polovici duljine vlaka, L/2, uvećanoj za udaljenost koju je vlak prešao u vremenu t_p:

­\( 1t_p = \frac{L}{2} + vt_p \)

Desinkronizacija ∆t je vremenska razlika između krmenog i pramčanog događaja u sustavu tračnica, tj. ∆t=t_p-t_k. Lako nalazimo

­\( 1\Delta t = 1(t_p – t_k) = v(t_p + t_k) \)

Ako uzmemo u obzir da je 1(t_p+t_k) prostorna udaljenost ∆s između krmenog i pramčanog događaja u sustavu tračnica, onda je 1∆t=v (∆s/1) .

Dakle, ako su dva događaja istovremena u sustavu koji se giba, onda su (u sustavu koji miruje) njihova vremenska udaljenost ∆t i njihova prostorna udaljenosti ∆s vezane s

­\( 1^2 \Delta t = v \Delta s \)

gdje je v brzina sustava koji se giba i c=1 (to je relacija koja nas iznenađuje, ako istovremenost u sustavu koji miruje smatramo apsolutnom).

Ako se dva događaja u sustavu koji se giba događaju na istom mjestu onda su njihova vremenska udaljenost ∆t i njihova prostorna udaljenost ∆s, u sustavu koji miruje, vezane s

­\( \Delta s = v \Delta t \)

gdje je v brzina sustava koji se giba (to je definicija brzine sustava koji se giba, na koju smo navikli).

• II

Sada uvodimo Epsteinove dijagrame koji će sve prethodne argumente učiniti gotovo trivijalnim. Prethodno razmatrani vagon-sat predstavljamo sljedećim dijagramom.

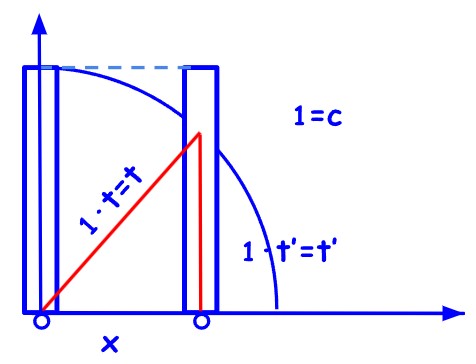
Osnovna jednadžba je

­\( x^2 + t’^2 = t^2 \)

Vrijeme t sustava u mirovanju naziva se koordinatno vrijeme. Vrijeme t’ sustava koji se giba naziva se vlastito vrijeme.

Ako osnovnu jednadžbu ­\( x^2 + t’^2 = t^2 \) podijelimo s t², dobivamo ekvivalentnu jednadžbu

­\( \frac{x^2}{t^2} + \frac{(t’)^2}{t^2} = 1 \)

koja povezuje dvije brzine. Brzinu u prostoru \( \frac{x}{t} = \dot{x} \) i brzinu u vlastitom vremenu \( \frac{t’}{t} = \dot{t’} \). Prva mjeri brzinu prostornog udaljavanja sustava, a druga brzinu njegovog vremenskog starenja. Te dvije brzine, kroz prostor i kroz vlastito vrijeme, dvije su komponente brzine \( (\dot{x}, \dot{t’}) \) kroz prostor-vrijeme, čiji je ukupni iznos, \( \sqrt{\frac{x^2}{t^2} + \frac{(t’)^2}{t^2}} = 1 \), jednak brzini svjetlosti. U tom smislu je brzina svakog sustava u prostor-vremenu jednaka brzini svjetlosti.

Epsteinov dijagram je stilizirani dijagram našeg vagona-sata (ako ste upoznati s geometrijom Minkowskog, primijetite da to nije x,t – dijagram Minkowskog):

­

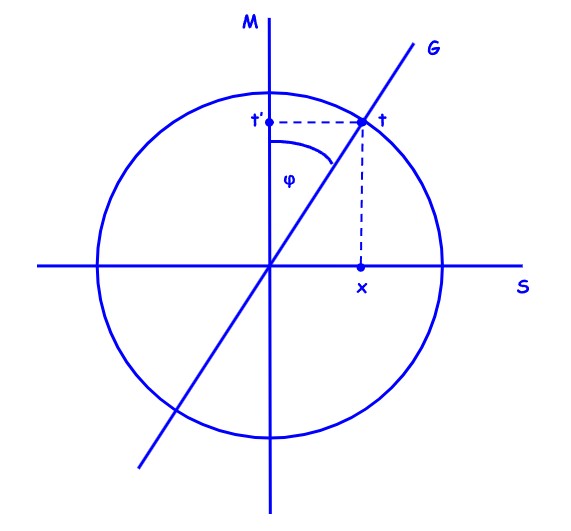
­\( \frac{x}{t} = v = \sin \varphi, \quad \frac{t’}{t} = \sqrt{1 – v^2} = \cos \varphi \)

To je x,t‘-dijagram. Usporedimo tri sustava u tom dijagramu. Dva ekstremna, M (sustav koji miruje, tj. giba se brzinom 0) i S (sustav zrake svjetlosti koja se giba brzinom 1) i sustav G (koji se u odnosu na M giba nekom brzinom između 0 i 1). Dakle, u odnosu na sustav M koji miruje imamo sljedeće slučajeve.

G se kreće brzinom v u prostoru x i stari brzinom \( \sqrt{1 – v^2} \) u vlastitom vremenu t‘:

­\( x = vt, \quad t’ = \sqrt{1 – v^2} , t \)

M miruje u prostoru x i najbrže stari u vlastitom vremenu t‘ (to je sustav najbržeg starenja):

­\( x = 0, \quad t’ = t \)

S se najbrže giba u prostoru x, no uopće ne stari u vlastitom vremenu t’ (to je sustav najsporijeg starenja):

­\( x = t, \quad t’ = 0 \)

Koristeći Epsteinov dijagram i malo matematike veoma je lako izvesti prethodne rezultate o kontrakciji vremena i prostora te o desinkronizaciji.

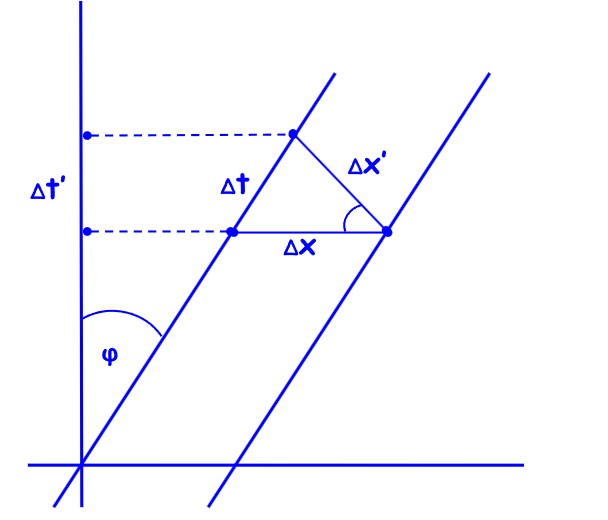
Paralelni pravci predstavljaju gibanje pramca i krme vagona koji se kreće brzinom v = sin ⁡φ. Desinkronizaciju ∆t kao i kontrakciju vremena ∆t‘ i prostora ∆x‘ veoma je lako izračunati iz dijagrama:

­\( \Delta t = \Delta x \sin \varphi = \Delta x v \)

­\( \Delta t’ = \Delta t \cos \varphi = \Delta t \sqrt{1 – v^2} \)

­\( \Delta x’ = \Delta x \cos \varphi = \Delta x \sqrt{1 – v^2} \)

Koristeći jedan drugi Epsteinov dijagram i malo više matematike, lako je izvesti slavne Lorentzove transformacije.

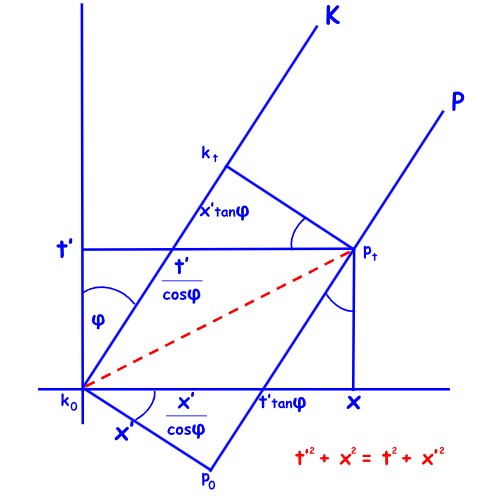
K predstavlja gibanje krme, a P gibanje pramca vagona. Točka k₀ predstavlja krmu u trenutku 0 (koji je sinkroniziran u sustavu tračnica i sustavu vagona). Točka p₀ predstavlja pramac u trenutku 0. Točka k_t predstavlja krmu u trenutku t. Točka p_t predstavlja pramac u trenutku t.

Koristeći se dijagramom, lako je izračunati x,t-koordinate iz x’,t’-koordinata:

­\( x = \frac{x’}{\cos \varphi} + t’ \tan \varphi, \quad t = \frac{t’}{\cos \varphi} + x’ \tan \varphi \)

­\( x = \frac{x’}{\sqrt{1 – v^2}} + \frac{t’v}{\sqrt{1 – v^2}} = \frac{x’ + t’v}{\sqrt{1 – v^2}}, \quad t = \frac{t’}{\sqrt{1 – v^2}} + \frac{x’v}{\sqrt{1 – v^2}} = \frac{t’ + x’v}{\sqrt{1 – v^2}} \)

Rješavanjem ovih linearnih jednadžbi za x’ i t’ dobivamo Lorentzove transformacije:

­\( x’ = \frac{x – vt}{\sqrt{1 – v^2}}, \quad t’ = \frac{t + xv}{\sqrt{1 – v^2}} \)

Primijetite da x,t’–pravokutnik i x’,t–pravokutnik imaju zajedničku dijagonalu pa slijedi

­\( x^2 + (t’)^2 = (x’)^2 + t^2 \quad tj. \quad (t’)^2 – (x’)^2 = t^2 – x^2 \)

To je dokaz da prostorno-vremenska udaljenost Minkowskog, t² – x², ne ovisi o sustavu.

• III

Za one koji su naučili specijalnu teoriju relativnosti pomoću dijagrama Minkowskog dajemo još i usporedbu njegovih i Epsteinovih dijagrama (koji su, nažalost, gotovo nepoznati). Prije svega podsjetimo da su Epsteinovi dijagrami x,t’–dijagrami, dok su dijagrami Minkowskog x,t–dijagrami. Dakle, postoji neko “gadno” miješanje koordinata u Epsteinovim dijagramima.

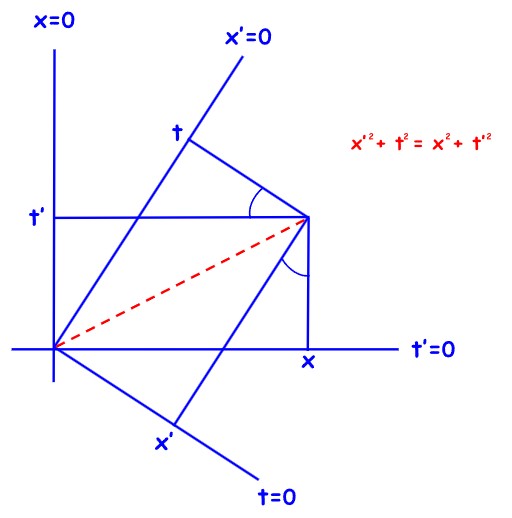
To znači da se t iščitava s pravca x’=0, a x se iščitava s pravca t’=0. Slično, t’ se iščitava s pravca x=0, a x’ se iščitava s pravca t=0.

Koordinate su izmiješane, ali su euklidske. Primijetite jednostavan euklidski argument (preko zajedničke dijagonale dvaju pravokutnika) za ključnu relaciju Minkowskog

­\( x^2 + (t’)^2 = (x’)^2 + t^2 \quad tj. \quad (t’)^2 – (x’)^2 = t^2 – x^2 \)

U dijagramima Minkowskog nema “gadnog” miješanja koordinata, t se iščitava s pravca x=0, a x se iščitava s pravca t=0. Slično, t’ se iščitava s pravca x’=0, a x’ se iščitava s pravca t’=0.

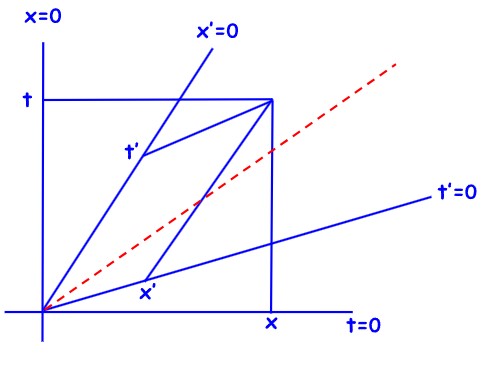
Koordinate nisu izmiješane, ali nisu ni euklidske. Zato nemamo jednostavan euklidski argument za ključnu relaciju Minkowskog t’² – x’²= t² – x², nego za njeno dokazivanje trebamo hiperboličku geometriju.

Primijetite da i Epstein i Minkowski predstavljaju 4 varijable t,x,t’,x’ pomoću dijagrama koji su 2-dimenzionalni. Njihova temeljna veza t’² – x’²= t² – x², ima euklidsku reprezentaciju u Epsteinovom dijagramu i hiperboličku reprezentaciju u dijagramu Minkowskog.

Ali 4 varijable t,x,t’,x’ prirodno je reprezentirati u 4-dimenzionalnom prostoru u kojem je njihova temeljna veza t’² – x’²= t² – x² reprezentirana 3-dimenzionalnom hiperplohom zadanom tom jednadžbom. Reprezentacije Epsteina i Minkowskog su dvije različite 2-dimenzionalne projekcije te temeljne 3-dimenzionalne hiperplohe. One predstavljaju tu temeljnu hiperplohu na dva različita načina (analogno 2-dimenzionalnim prikazima 3-dimenzionalnih objekata u deskriptivnoj geometriji pomoću tlocrta i nacrta).

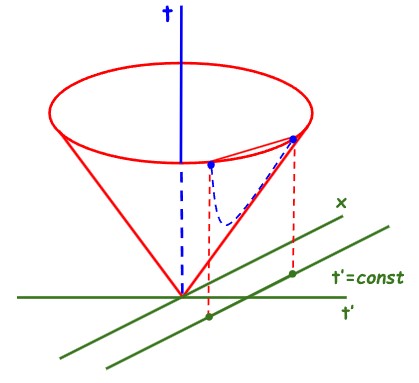
Naime, 3-dimenzionalnu hiperplohu u 4-dimenzionalnom prostoru nije lako ni zamisliti ni nacrtati. Stoga zamišljamo i crtamo njen 2-dimenzionalni presjek s x‘=0 (što odgovara promatraču koji miruje u sustavu koji se giba).

Presjek 3-dimenzionalne hiperplohe s x’=0 je konus

­\( x^2 + (t’)^2 = t^2 \)

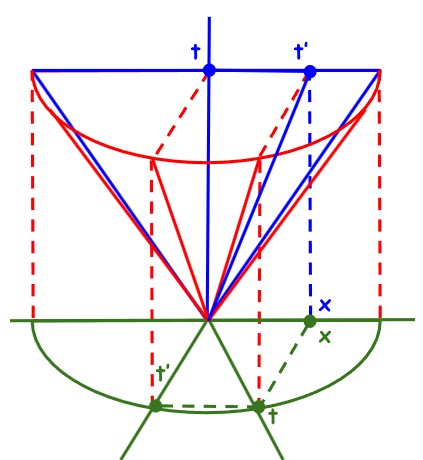
Pogled odozgo na konus, tj. njegova projekcija na x,t’–ravninu je Epsteinov (zeleni) dijagram. Pogled sprijeda na konus, tj. njegova projekcija na x,t–ravninu je (plavi) dijagram Minkowskog.

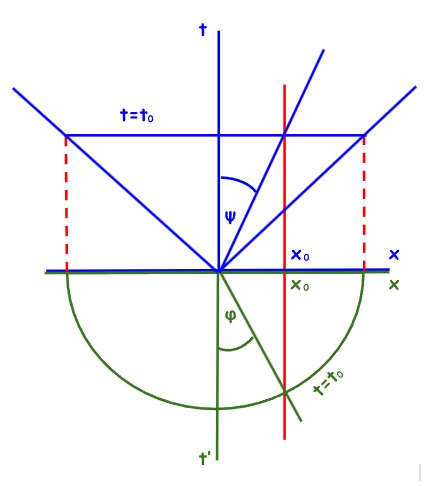
Sada je lako vidjeti kako se euklidska geometrija Epsteinove x,t’–ravnine transformira u hiperboličku geometriju x,t–ravnine Minkowskog. Istodobni događaji u sustavu koji miruje, u trenutku t = t₀, predstavljeni su krugom u Epsteinovom dijagramu i pravcem u dijagramu Minkowskog. To su pogled odozgo i pogled sprijeda na x² + t‘²= t₀².

Sustav koji se giba predstavljen je u Epsteinovom dijagramu pravcem s nagibom φ, a brzina mu je v = x/t = sin⁡ φ. U dijagramu Minkowskog predstavljen je pravcem s nagibom ψ, a brzina mu je v = x/t = tg⁡ ψ.

Prostor t’ = const je prostor istodobnih događaja u sustavu koji se giba. To je (euklidski) pravac u Epsteinovom dijagramu i hiperbola u dijagramu Minkowskog. Oni su pogled odozgo i pogled sa strane na

­\( t^2 = x^2 + \text{const}^2 \quad tj. \quad t^2 – x^2 = \text{const}^2 \)

Tako možemo nacrtati i 2-dimenzionalni presjek temeljne 3-dimenzionalne hiperplohe u 4-dimenzionalnom t,x,t’,x’ – prostoru s t‘=0 (što odgovara x‘-prostoru zamrznutom u trenutku t‘=0). Naravno, taj presjek je konus x’² + t²= x² u 3-dimenzionalnom t,x,x’-prostoru.

Pogled odozgo na konus, tj. njegova projekcija na x,t’–ravninu je Epsteinov dijagram. Pogled sa strane na konus, tj. njegova projekcija na x,t–ravninu je dijagram Minkowskog.

Odgovarajuće slike identične su prethodnima s x,t’ označenim kao x’,t. Događaji koji se događaju na istom mjestu x = x₀, u sustavu koji miruje, predstavljeni su krugom u Epsteinovom dijagramu i pravcem u Minkowskijevom dijagramu. To su pogled odozgo i pogled sprijeda na x² + t’²= t₀².

Zaključimo, dijagrami Epsteina i Minkowskog su 2-dimenzionalne projekcije iste 3-dimenzionalne relacije između t,x,t’ i x’:

­\( x^2 + (t’)^2 = (x’)^2 + t^2 \quad tj. \quad (t’)^2 – (x’)^2 = t^2 – x^2 \)

Oba dijagrama predstavljaju taj odnos, jedan na euklidski, a drugi na hiperbolički način.

Naravno, ako imamo 3 prostorne koordinate x,x’,y,y’,z i z’, onda imamo posla s 8 varijabli t,x,y,z,t’,x’,y’,z’ koje su matematički predstavljene u 8-dimenzionalnom prostoru, a njihova ključna veza

­\( t’^2 – x’^2 – y’^2 – z’^2 = t^2 – x^2 – y^2 – z^2 \)

predstavljena je 7-dimenzionalnom hiperplohom zadanom ovom jednadžbom. Epsteinov i Minkowskijev dijagram sada su 4-dimenzionalne projekcije ove 7-dimenzionalne hiperplohe i oba predstavljaju tu vezu; jedan na euklidski, a drugi na hiperbolički način.

• Reference:

[1] Einstein, A. Zur Elektrodynamik bewegter Koerper, Annalen der Physik, 322 (10), pp. 891–921, 1905.

[2] Epstein, L.C. Relativity visualized, Insight Press, 1983.

[3] Minkowski, H. Raum und Zeit, Physikalische Zeitschrift, 10, pp. 75–88, 1909.