Formalizacije logike sudova. Frege i Kneale, generatori i testovi

U četvrtom nastavku serijala o povijesti logike, Zvonimir Šikić pokazuje kako su Fregeov modus ponens i minimalna logika evoluirali u Knealeove multiplarne dedukcije koje zatvaraju krug korektnosti, potpunosti i odlučivosti.

• Naslovna fotografija: Njemački logičar i matematičar Gottlob Frege (lijevo), engleski filozof William Kneale (desno). (CC0)

• Prethodni članci u seriji: Logička korektnost, potpunost i kompaktnost. Gentzenov IF-sustav i Bethova semantička stabla, Zaključivanje u prirodnom i artificijelnom jeziku. Od Aristotela prema Fregeu, Logika sudova. Kondicionali, bikondicionali i implikacije

­

1. Fregeovi aksiomi i Gentzenove prirodne dedukcije

Istinosno funkcionalno shvaćanje veznika pripisuje se već stoiku Krizipu iz 3. st. pr. n. e. J. Venn je tehniku „križića i iscrtkavanja“ uveo 1880. Tehnika istinosnih tablica nalazi se u spisima C. S. Peircea već u 1880-tima, a prvi su je objavili E. Post 1921. i L. Witgenstein 1922. u Tractatusu. Metodu semantičkih stabala, kao postupak dokazivanja, u logiku je 1955. uveo E.W. Beth. Prije toga su sustavi dokazivanja u logici, po uzoru na matematičke teorije, najčešće formulirani kao aksiomatske teorije.

Prvu takvu aksiomatizaciju, onu G. Fregea iz 1879, mnogi smatraju rođenjem moderne logike. Fregeovi aksiomi za istinosno funkcionalni dio njegove mnogo obuhvatnije logike (kojom je pokušavao dokazati logicističku tezu da matematika zapravo nema svojih posebnih aksioma, nego da oni slijede iz logičkih aksioma) bili su (F1) – (DNE) te pravilo zaključivanja (MP).

FREGEOV AKSIOMATSKI IF-SUSTAV

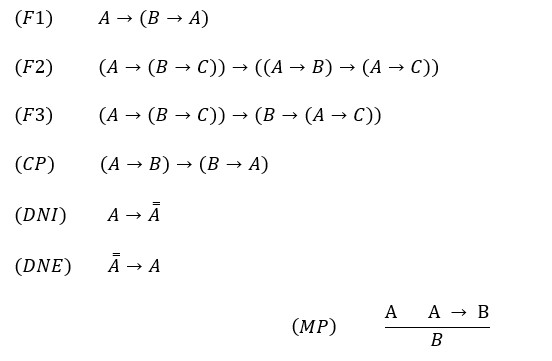
Zadnja tri aksioma označili smo latinskim kraticama njihovih pred fregeovskih imena: (CP) za kontrapoziciju, (DNI) za introdukciju dvostruke negacije i (DNE) za eliminaciju dvostruke negacije. Fregeovo jedino pravilo izvođenja je pravilo modus ponens (MP). Dokaz forme A je konačno stablo formi na čijem je dnu (korijenu) forma A, na čijim vrhovima (listovima) su aksiomi i u kojem svaka forma koja nije na vrhu slijedi iz onih neposredno iznad nje primjenom pravila (MP).

Svi aksiomi očito su valjane forme, a i (MP) iz dvije valjane forme izvodi valjanu formu. Dakle, u Fregeovom sustavu dokazive su samo valjane forme, tj. Fregeov sustav je semantički korektan. Uskoro ćemo dokazati da je i potpun.

Problem Fregeovog sustava jest da je u njemu teško nalaziti dokaze. Pokušajte npr. dokazati formu A → A. Pronalaženje ovakvih dokaza, i što je još važnije, nekih općih principa koji vode k nalaženju takvih dokaza, bila je jedna od glavnih zadaća kojima su se bavili logičari s početka 20. st.

Najuspješnija ideja bila je da se osim izvoda iz aksioma dopuste i izvodi iz pretpostavki. To znači da se osim dokaza sekventi oblika ⊢ A dokazuju i sekvente oblika Γ ⊢ A. Naravno, dokaz sekvente Γ⊢A konačno je stablo na čijem je dnu forma A, na čijim su vrhovima aksiomi ili formule iz Γ i u kojem svaka forma koja nije na vrhu slijedi iz onih neposredno iznad nje primjenom pravila (MP).

Budući da pravilo (MP) sada primjenjujemo i na forme izvedene iz pretpostavki, ono je nešto općenitije:

­­

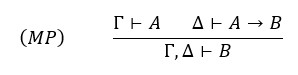
Dokazi postaju bitno jednostavniji ako se koristimo i drugim pravilima zaključivanja koja su izvediva u Fregeovom sustavu. Najjednostavnije takvo pravilo je teorem dedukcije:

­­

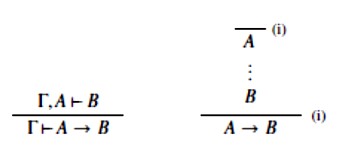
Desno je teorem dedukcije u tzv. prirodnom obliku. On se koristi kako je zapisano u lijevom sekventnom formatu. Dakle, ako smo polazeći od pretpostavki Γ, A izgradili stablo koje završava s B, u sljedećem koraku možemo izvesti A → B i pritom odbaciti pretpostavku A. Odbacivanje pretpostavke označava se crtom iznad nje, a indeksi (i) naznačuju u kojem je koraku pretpostavka odbačena.

Kao ilustraciju dokazujemo da je kondicional tranzitivan, tj. A → B, B → C ⊢ A → C.

­­

To je mnogo teže izvesti samo uz pomoć (MP) iz Fregeovih aksioma. Zato je Łukasiewicz tek 1939. g. uspio dokazati da je Fregeov aksiom (F3) izvediv iz (F1), (F2) i (MP). Uz teorem dedukcije dokaz je postao trivijalan:

­­

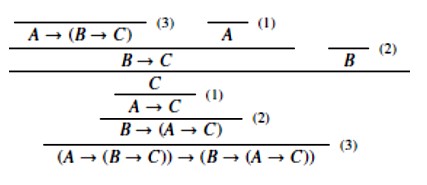
Teorem dedukcije zapravo je pravilo introdukcije veznika →, dok je modus ponens pravilo eliminacije veznika →. Zato se ta pravila označavaju s (I →) i (E →).

­­

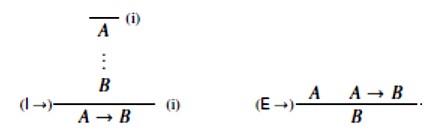
U Fregeovom sustavu vrijede i pravila introdukcije i eliminacije negacije (primijetimo da su to posebni slučajevi od (I →) i (E →) ako \(\small \overline{A} \overset{def}{\Longleftrightarrow} A \rightarrow \bot\).

­­

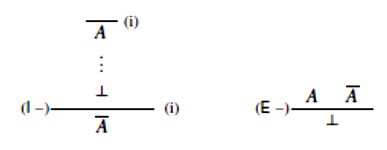
Može se relativno lako dokazati da su ta četiri pravila zaključivanja zajedno s (DNE) ekvivalentna početnom Fregeovom sustavu.

Aksiomatske dokaze teško je konstruirati pa je put prema pravilima prirodan i praktički nužan. Sljedeći korak, koji je učinio G. Gentzen 1934. jest da se odmah krene od pravila introdukcije i eliminacije, a da se aksiomi naprosto zaborave. Tako je nastala tradicija da se logika formulira kao sustav prirodnih dedukcija.

Osnovne su karakteristike takvih sustava da su njihovi izvodi izvodi iz pretpostavki, da svaki logički simbol ima svoja pravila introdukcije i eliminacije i da su pravila introdukcije i eliminacije za pojedini logički simbol (ili grupu logičkih simbola) potpuna za taj simbol (ili grupu). Treća karakteristika više je smjernica nego realizirana karakteristika jer ju većina sustava ispunjava samo uz iznimke.

U tom smislu je sustav pravila (I→), (E→), (I —), (E —) i (DNE) sustav prirodnih dedukcija za IF-logiku, u kojem (DNE) donekle odskače (iako ga možemo smatrati još jednom eliminacijom negacije). Veznici ∧ i ∨ u njemu se mogu definirati na standardni način, \(\small A \land B \overset{def}{\Longleftrightarrow} \neg(A \rightarrow \overline{B}) \) i \(\small A \lor B \overset{def}{\Longleftrightarrow} \overline{A} \rightarrow B\), no češće se nezavisno formuliraju njihova pravila introdukcije i eliminacije (koja inače lako slijede iz prethodnih definicija). Tako dolazimo do Gentzenovog IF-sustava prirodnih dedukcija.

GENTZENOV IF-SUSTAV PRIRODNIH DEDUKCIJA

­­

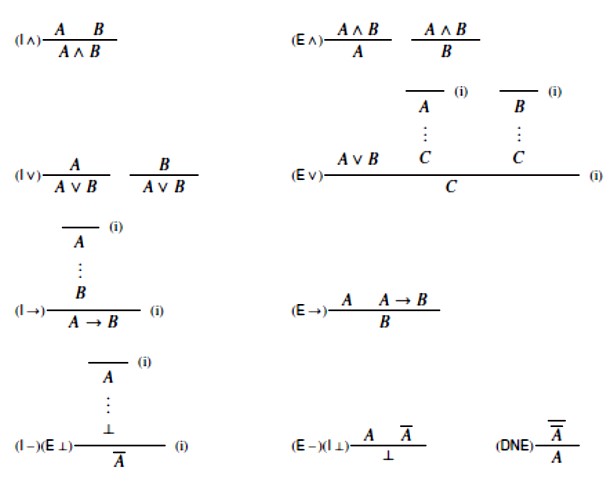
Taj je sustav semantički korektan, jer je ekvivalentan Fregeovom semantički korektnom sustavu. On je i potpun jer se u njemu može dokazati svaka sekventa koja je dokaziva u Gentzenovom sekventnom IF-sustavu, čiju smo potpunost dokazali u prethodnom poglavlju. To se dokazuje tako da se usporede Gentzenov prirodni i sekventni sustav. Prvo se uvodi Gentzenov singularni sustav čije sekvente imaju najviše jednu konkluziju kao i njegov prirodni sustav. Zatim se relativno lako dokazuje da sva pravila Gentzenovog multiplarnog sustava, uz dodano pravilo (DNE), slijede već iz njihovih singularnih restrikcija. No, to znači da je Gentzenov singularni sustav proširen s (DNE) potpun.

S druge strane sve što je dokazivo u Gentzenovom singularnom sustavu proširenom s (DNE) dokazivo je i u Gentzenovom sustavu prirodnih dedukcija pa je i on potpun. Naime, primjena svakog pravila singularnog sekventnog sustava može se provesti u prirodnom sustavu. Na primjer, pravilo

­­

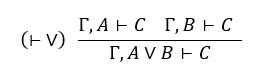
zapravo kaže da se izvod od C iz Γ, A i izvod od C iz Γ, B može prevesti u izvod od C iz Γ, A ∨ B, a to se očito može provesti i u prirodnom sustavu:

­­

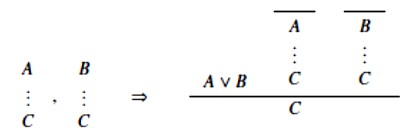
Na isti način, pravilo

­­

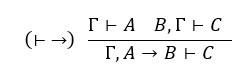
kaže da se izvod od A iz Γ i izvod od C iz B, Γ može prevesti u izvod od C iz Γ, A → B, a i to se može provesti u prirodnom sustavu:

­­

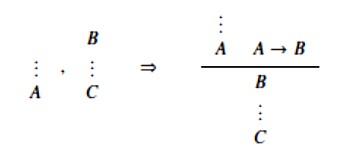
Isto vrijedi za sva ostala pravila, što se lako provjerava.

Dodajmo da je Gentzenov sustav prirodnih dedukcija bez (DNE) tzv. minimalna logika. Ako njoj dodamo pravilo ex falso quodlibet („iz kontradikcije bilo što“) dobivamo intuicionističku logiku. Ako njoj dodamo aksiom tertium non datur („trećeg nema“) dobivamo standardnu (klasičnu) IF-logiku, jer su (EFQ) i (TND) uzeti zajedno ekvivalentni s (DNE).

­­

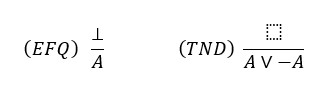
Ako vrijede (EFQ) i (TND) onda vrijedi i (DNE):­­

­­

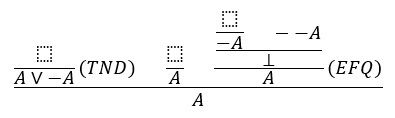
Ako vrijedi (DNE) onda vrijede i (EFQ) i (TND):

­­

2. Knealove multiplarne prirodne dedukcije

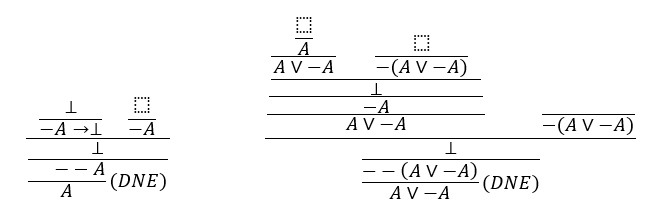
Zapravo smo mogli krenuti i direktno od sekventnih multiplarnih pravila kao uputa za konstruiranje prirodnih dedukcija pomoću prirodnih multiplarnih pravila. Na primjer, sekventno multiplarno pravilo

­­

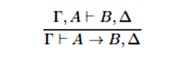
zapravo kaže da se izvod od B, Δ iz Γ, A može prevesti u izvod od A → B, Δ iz Γ. To se očito može provesti pomoću prirodnih multiplarnih pravila

­­

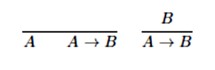
na sljedeći način

­­ ­

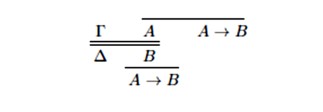
Jednako tako se i sekventna multiplarna pravila za negaciju

­­

mogu provesti pomoću prirodnih multiplarnih pravila

­­

na sljedeći način

­­

Uvedemo li na isti način prirodna multiplarna pravila za ostale veznike dolazimo do IF-sustava prirodnih multiplarnih dedukcija koji je formulirao W. Kneale 1962. i koji je očito potpun (jer može izvesti sve što može i Gentzenov multiplarni sustav za koji znamo da je potpun).

KNEALEOV IF-SUSTAV PRIRODNIH MULTIPLARNIH DEDUKCIJA

­­

(Zadnja dva pravila zapravo tvrde da je Γ ⊢ Δ, A, A isto što i Γ ⊢ Δ, A te da je Γ, A, A ⊢ Δ isto što i Γ, A ⊢ Δ.)

Dokaz sekvente Γ ⊢ Δ je graf bez zatvorenih ciklusa na čijim su vrhovima forme iz Γ, na čijim su dnima forme iz Δ i u kojem je veza formi iznad i ispod svake crte primjena nekog Knealovog pravila. Zatvoreni ciklusi nisu dopušteni, jer dovode do pogrešnih izvoda poput ovog:

­­

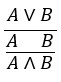
Kao primjer, evo izvoda dobro poznatih DeMorganovih zakona

­­

Spomenimo na kraju da je Knealeova ideja bila da formulira sustav dedukcija u kojem su sva pravila jednostavna, tj. da njihova primjena ovisi samo o formama na koje se ona neposredno primjenjuju. Na primjer Gentzenovo pravilo (I ∧) A, B / A ∧ B je jednostavno, ali Gentzenovo pravilo (I→) B/A → B nije jednostavno, jer njegova primjena uključuje odbacivanje svih pretpostavki A (dakle, ne ovisi samo o formi B na koju se (I→) neposredno primjenjuje).

Knealova pravila za sve IF-veznike zaista su jednostavna u tom smislu, ali zadnja dva pravila njegovog sustava (koja odbacuju ponovljene pretpostavke i ponovljene konkluzije) nisu jednostavna. Zapravo, Knealeov originalni sustav ne uključuje ta pravila. To je njegov sustav činilo nepotpunim, čega Kneale nije bio svjestan (to su dokazali Shoesmith i Smiley 1978.).

Postoje i druge formalizacije logike sudova osim ovdje spomenutih, no ove koje smo opisali vjerojatno su najzanimljivije.

3. Testovi i generatori

Sustavi dokaza generiraju implikacije i valjane forme, dok ih metoda istinosnih tablica i Bethova metoda testiraju. Koja je veza, sasvim općenito, između generatora i testova?

Generator G generira određeni tip objekata. Za svaki objekt x toga tipa možemo se pitati generira li ga taj generator: G ↣ x?

Test T testira određeni tip objekata. Za svaki objekt x toga tipa možemo se pitati je li on prošao taj test: T(x)= + ?

Svaki generator G možemo shvatiti kao test pozitivnosti: G(x)= + tada znači G ↣ x.

Svaki test pozitivnosti T možemo shvatiti kao generator: T ↣ x tada znači T(x)= +.

Važno je razumjeti da su testovi gotovo uvijek testovi pozitivnosti i negativnosti. Naime, kada T testira x on najčešće daje odgovor T(x)= + ili T(x)= – . Takvi testovi zovu se testovi odluke i jači su od generatora koji su ekvivalentni testovima pozitivnosti. Dakle, testovi pozitivnosti nisu nužno testovi odluke. Na primjer, jednostavni test kojim testiramo je li neki skup konačan može se sastojati u tome da vadimo elemente iz tog skupa dok ne dođemo do praznog skupa. To je pozitivni test ali nije test odluke (ako je x konačan skup test će to utvrditi, tj, T(x)= +, ali ako x nije konačan test to neće utvrditi).

Korektnost i potpunost generatora G za svojstvo S definira se ovako:

\(\small \mathcal{G} \text{ korektan za } S \overset{def}{\Longleftrightarrow} (\mathcal{G} \rightarrow x) \Rightarrow S(x)\)

\(\small \mathcal{G} \text{ potpun za } S \overset{def}{\Longleftrightarrow} S(x) \Rightarrow (\mathcal{G} \rightarrow x)\)

Dakle,

\(\small \mathcal{G} \text{ korektan i potpun za } S \overset{def}{\Longleftrightarrow} (\mathcal{G} \rightarrow x) \Longleftrightarrow S(x)\)

Pozitivnost i negativnost testa T za svojstvo S definira se ovako:

\(\small \mathcal{T} \text{ je pozitivan za } S \overset{def}{\Longleftrightarrow} (\mathcal{T}(x) = +) \Longleftrightarrow S(x)\)

\(\small \mathcal{T} \text{ je negativan za } S \overset{def}{\Longleftrightarrow} (\mathcal{T}(x) = +) \Longleftrightarrow -S(x)\)

Test T je test odluke za svojstvo S akko je pozitivni i negativni test za S.

Dakle, generator G je korektan i potpun za S akko je pozitivan za S (shvatimo li ga kao pozitivni test). S druge strane, test T je pozitivan za S akko je korektan i potpun za S (shvatimo li ga kao generator).

Vratimo se logici sudova. Metoda istinosnih tablica i Bethova metoda semantičkih stabala testovi su odluke za implikaciju i valjanost. Svi sustavi dokazivanja opisani u ovom poglavlju (Fregeov, oba Gentzenova i Knealeov) korektni su i potpuni generatori za implikacije i valjane forme.

U jednom od sljedećih poglavlja dokazat ćemo da je Bethova metoda semantičkih stabala pozitivni test za implikacije logike predikata, ali nije test odluke. (Metoda istinosnih tablica uopće ne postoji za logiku predikata.) Sustavi dokazivanja (Fregeov, oba Gentzenova i Knealeov) koje ćemo proširiti na logiku predikata i dalje će biti korektni i potpuni generatori implikacija i valjanih formi. Zato se za logiku sudova kaže da je odlučiva, a za logiku predikata da je potpuna.