Kakve veze (ako ikakve) imaju matematika i stvarnost. Od neba preko Zemlje do skupova.

Milenijima je status matematike među znanostima a i sama njezina priroda predmet diskusija i suprotstavljenih shvaćanja. Zvonimir Šikić počinje od Antike, opisuje odnos matematike i prirodnih znanosti u osvit Novog vijeka, a završava ulogom teorije skupova kako u opisu njezine 'ontološke pozicije' tako i rigoroznosti kao temeljne osobine matematike (bez obzira na sve)

• Nakon razgovora o Knjizi za klikeraše Zvonimira Šikića, koji su Ideje.hr upriličile u proljeće, a koji je prenio i Treći program Hrvatskog radija, isti je medij, u koordinaciji s našim uredništvom, objavio i dijelove ovog eseja. Ideje.hr ga sad bilježe u cjelovitom obliku

Matematika nije prirodna znanost. Prirodne znanosti imaju svoj konkretni predmet, koji izučavaju otvorenih očiju u svojim laboratorijima. (Laboratoriji mogu biti tek zabiti kutci nekog sveučilišta, ali se mogu i proširiti na cijeli univerzum.) Taj konkretni predmet prirodnih znanosti jest materijalni svijet. Matematika se ne bavi tim konkretnim predmetom. Ona se bavi svojim apstraktnim predmetom i izučava ga zatvorenih očiju.

Kada matematika dokazuje da zbroj kutova u svakom trokutu ima 180^o, ona se ne bavi konkretnim, osjetilima dostupnim trokutima materijalnog svijeta, nego se bavi apstraktnim, umu dostupnim trokutima koje nalazi u svijetu ideja. Trokuti o kojima je riječ u matematici protežu se u samo dvije dimenzije, omeđeni su dužinama koje se protežu u samo jednoj dimenziji, a same te dužine sastaju se u vrhovima koji su bez ikakve protežnosti. Takvi predmeti ne postoje u materijalnom svijetu. No, samo o takvim apstraktnim predmetima matematika može s izvjesnošću izricati svoje istine.

Matematika je izvjesna znanost, jer se bavi apstraktnim predmetima o kojima je moguće izvjesno znanje. Prirodne znanosti nisu izvjesne, jer se bave konkretnim predmetima o kojima izvjesno znanje nije moguće. Zato se istine prirodnih znanosti, koje su uvijek relativne i podložne sudu vremena, bitno razlikuju od matematičkih istina, koje su apsolutne i vječne.

Ova, donekle shematizirana slika matematike i prirodnih znanosti s nama je već dva i pol milenija. Točnije, od klasičnog grčkog razdoblja u kojem je matematika konstituirana kao znanost o čistim formama ili idejama. Tada je, u potrazi za izvjesnim, napušten konkretni svijet materijalne prirode, i otkriven apstraktni svijet čistih matematičkih formi, svijet ideja.

Prvi je svijet nepostojan. U njemu stvari nastaju i nestaju, rađaju se i umiru. To je kvarljiv svijet materije u kojem “stalna samo mijena jest”. Drugi je svijet postojan. U njemu stvari niti nastaju niti nestaju, niti se rađaju niti umiru. To je nekvarljiv svijet vječnih i nepromjenljivih matematičkih formi, svijet ideja. Između ta dva bitno različita svijeta otvoren je ponor.

Zbroj kutova nekog materijalnog, osjetilima dostupnoga trokuta uvijek je nešto približno, ako uopće i jest nešto. Tek o neosjetilnoj ideji trokuta možemo s izvjesnošću tvrditi da zbroj njezinih kutova ima 180^o. No mi tu izvjesnu spoznaju o trokutu, kao čistoj matematičkoj formi, primjenjujemo i kada se bavimo materijalnim, osjetilima dostupnim trokutima. Je li to opravdano? Je li matematika primjenljiva?

Pitagora, prema legendi, odgovara potvrdno. Ideja trokuta je konstitutivni element materijalnog trokuta, koji nam tek omogućuje da taj materijalni trokut istinski spoznamo. Istinska stvarnost prirode nije u kvarljivoj materiji, nego je u postojanoj formi, proporciji i broju. Kada Pitagora kaže da je priroda brojevna, time nam govori da je matematika primjenljiva.

Ovaj uvid, koji potječe iz ranoga djetinjstva matematike i filozofije, danas ravna znanošću kao njezino vodeće načelo. Ipak, u klasičnom grčkom razdoblju on je bio odbačen i proteklo je dvije tisuće godina prije njegovog slavodobitnog povratka kroz djela Kopernika,  Galilea i ostalih novovjekovnih pitagorejaca.

Naime, pokušaji da se svijet materije uskladi sa svijetom ideja često su vodili paradoksalnim zaključcima. Zenonovi paradoksi primjer su takvog zaključivanja. Može li strijela preletjeti jedan stadij? Da bi preletjela jedan stadij, najprije mora preletjeti pola stadija. No, da bi preletjela pola stadija, prije toga mora preletjeti polovicu te polovice. Da bi preletjela polovicu te polovice stadija, najprije mora preletjeti polovicu polovicine polovice, i to se ponavlja u beskonačnost. Može li strijela učiniti prvi pomak? Zenonova je poruka da ne može. To je, naravno, paradoksalno.  Svatko se može uvjeriti u let strijele.

S druge strane nema ničeg paradoksalnog u tome da se apstraktna matematička dužina može beskonačno dijeliti, na sve kraće i kraće dužine. No, može li se tako dijeliti konkretna putanja strijele ili ona ima najmanji početni dio, “prvi pomak”? Ne proizlazi li paradoksalni zaključak iz neopravdane identifikacije apstraktne matematičke dužine s konkretnom putanjom strijele? Nije li paradoks rezultat neopravdane primjene apstraktne  matematike na konkretnu putanju? Do sličnih paradoksa dolazi i Demokrit kada svoju atomističku koncepciju konkretnog svijeta materije pokušava uskladiti s kontinuiranošću apstraktnog matematičkog prostora. Čini se da matematika nije primjenjiva.

Za Platona je mathema, izvjesno znanje o svijetu ideja, jedina istinska znanost, jedina episteme. Matematika nije primjenjiva na kvarljiv svijet materije, pa istinska znanost o tom svijetu nije moguća.

Kroz djelo Platona i Aristotela ovo negiranje primjenjivosti matematike postalo je velikom filozofijskom tradicijom. Za Platona je mathema, izvjesno znanje o svijetu ideja, jedina istinska znanost, jedina episteme. Matematika nije primjenjiva na kvarljiv svijet materije, pa istinska znanost o tom svijetu nije moguća. Episteme physike je kontradiktoran pojam.

Aristotel se slaže s osnovnom tezom o neprimjenjivosti matematike, ali ne misli da je mathema jedini izvor znanja. Znanost o materijalnom svijetu je moguća, iako ne kao mathema nego kao historie, kao empirijsko znanje koje se stječe opažanjem. Dakle, fizika je doxa, vjerojatno mnijenje, čiji je izvor historie. Matematička fizika, u kojoj bi matematika bila primjenjiva, nije moguća. Zato je Aristotel fiziku i ostale prirodne znanosti utemeljio kao empirijske nematematizirane znanosti.

Njegova nematematička, empirijska fizika razlikuje četiri elementa: zemlju, vodu, zrak i vatru. Svaki element ima svoju prirodu, physis, u skladu s kojom se kreće. Teži elementi zemlja i voda prirodno se kreću dolje, prema središtu svijeta, dok se lakši elementi vatra i zrak prirodno kreću gore, od njegova središta. Tvari ispod Mjeseca u različitim su omjerima kombinacije četiriju elemenata i kreću se u skladu s tim omjerima. Teške tvari, koje pretežno sadrže zemlju, smjestit će se u središte svijeta. Njihovu će površinu prekriti nešto lakše tvari, koje pretežno sadrže vodu. Iznad njih lebdjet će još lakše tvari, koje pretežno čini zrak. Kroz sve to i iznad svega toga probijat će se najlakša tvar, vatra.

Već ovaj kratki opis dovoljan je da uočimo kako je Aristotelova fizika u suglasju sa svagdanjim iskustvom. Ona je, naime, neposredni rezultat opažanja. Takva je i njegova biologija. Kada istražuje ontogenezu Aristotel dan za danom razbija jaja i neposrednim opažanjem prati razvoj organizma, od svježeg jajeta do tek izlegnutog pileta. Dakle, prirodne znanosti, svjesnom odlukom njihova začetnika, počinju kao empirijske nematematizirane znanosti, jer njihov nepostojani predmet nije podložan matematizaciji.

Kada istražuje ontogenezu Aristotel dan za danom razbija kokošja jaja i neposrednim opažanjem prati razvoj organizma, od svježeg jajeta do tek izlegnutog pileta. To nije matematika, to je varljivo znanje

S druge strane, astronomija je oduvijek bila matematizirana. Njezin predmet su nepromjenljive nebeske konstelacije sa svojim pravilnim periodičkim gibanjima, koja su se opažala i bilježila i tisuće godina prije Grka. Taj postojani nekvarljivi predmet očito je podložan  matematizaciji i Grci ga ne smatraju materijalnim. Nebeske sfere su eterične. Sublunarno područje izgrađeno je od četiri kvarljiva elementa, zemlje, vode, vatre i zraka, dok je supralunarno nebesko područje, područje nekvarljivog etera.

Najveći matematičar klasične Grčke, Platonov učenik i prijatelj Eudokso, utemeljio je matematičku astronomiju koja jednolikim međusobno uklopljenim kružnim gibanjima nebeskih sfera objašnjava opažena gibanja ‘lutajućih zvijezda’, planeta. Međutim, Eudoksov planetarni model nije bio potpuno usklađen s opažanjima. Sunce ne prelazi sva četiri kvadranta Zodijaka u jednakim vremenskim intervalima. Razdoblje od solsticija do ekvinocija nije jednako razdoblju od tog ekvinocija do sljedećeg solsticija. Dakle, Sunce ne rotira oko Zemlje jednolikom brzinom. Osim toga, prividna svjetlost planeta i prividna veličina Mjeseca promjenjive su. Dakle, njihove udaljenosti od Zemlje nisu konstantne, njihovo gibanje oko Zemlje nije kružno.

Aristarh, Arhimedov suvremenik, predložio je heliocentrični matematizirani sustav astronomije, koji je riješio neke od ovih problema. Međutim, ta ‘puka matematička hipoteza’, bila je u direktnoj suprotnosti sa sublunarnom Aristotelovom fizikom i Ptolemej će je pet stoljeća kasnije ismijavati u uvodu svojeg Almagesta. On sam je, koristeći se idejama mnogih matematičara, posebno Apolonija iz Perge, većinu tih problema riješio u tada prihvatljivijem geocentričnom sustavu, upotrebljavajući epiciklička gibanja. Nebeske sfere sa svojim ‘lutajućim zvijezdama’ ne gibaju se oko zajedničkog središta svijeta, nego se jedna kružnica giba oko središta koje se giba po drugoj kružnici, ova se opet giba oko središta koje se giba po trećoj kružnici itd. Takvim složenim epicikličkim gibanjima Ptolemej je uspješno opisao gibanja nebeskog svoda. Bio je to zadivljujući uspjeh matematizirane astronomije.

(Da je uistinu riječ o čisto matematičkoj teoriji pokazuje i sam naslov Ptolemejevog djela: Syntaxis mathematica, što znači Matematička zbirka. Kako bi je razlikovali od manje značajnih djela istoga naslova,  kasniji komentatori dodali su joj superlativ magiste, najveća, čemu su arapski prevoditelji dodali član al, pa je ona otada poznata kao Almagest.)

Dakle, s jedne strane nalazimo matematiku i matematičku astronomiju, čiji su predmet postojane ideje i nekvarljivi eter, dok s druge strane nalazimo nematematizirane empirijske prirodne znanosti čiji je predmet kvarljiva materija. Takav odnos matematike i prirodnih znanosti promijenjen je tek s pojavom novovjekovne matematičke fizike. Kako je ona nastala? Kako je nastala novovjekovna matematizirana empirijska prirodna znanost?

Često se kao glavna novost ističe empirijski karakter nove znanosti. To najbolje dokumentira Baconov poziv, iz 1620. godine, da se anticipatio mentis zamjeni s interpretatio naturae. Bacon se buni protiv Aristotela i njegovih skolastičkih sljedbenika koji se pozivaju na autoritet profesorovih knjiga i knjige otkrivenja. Autoritet samo stvara predrasude kojih se treba riješiti pa tako oslobođen prići neposrednom čitanju knjige prirode. (Inače, “predrasuda” je riječ koju je u europske jezike uveo Bacon.)

Ovaj je poziv bio značajan jer se Aristotelova doxa kroz dvije tisuće godina pretvorila u dogmu i njen je empirijski karakter u međuvremenu potpuno zaboravljen. Zato se može reći da se 1609. godine, kada je Galileo uperio svoj teleskop prema nebeskom svodu, zbio nov i uistinu važan događaj.

U Zvjezdanom glasniku (Sidereus nuncius) iz 1610. godine, Galileo izvještava da Mjesec nije savršena eterična kugla, nego je sa svojim brdima i dolinama vrlo sličan materijalnoj Zemlji. Ni samo Sunce nije savršeno. Na njemu se pojavljuju sunčeve pjege o kojima je Galileo izvijestio u posebnom spisu iz 1613. godine. Čini se da nebo nije tako postojano kako su mislili stari Grci. Uostalom, još 1572. godine Brache je na nebu opazio jednu super-novu koja je nastala, trajala osamnaest mjeseci i nestala. Nema, dakle, bitne razlike između neba i Zemlje.

Znači li to da matematička astronomija sada, kada je nebo spušteno na zemlju, više nije moguća? Ne znači, jer Zemlju su već prije toga Kopernik, Galileo i ostali novovjekovni pitagorejci “podigli na nebo”. Kopernik 1543. godine objavljuje heliocentrični sustav matematičke astronomije, De revolutionibis orbium coelestium, u kojem je Zemlja tek jedan od planeta koji kruže oko Sunca.

Takav je sustav u neposrednoj suprotnosti s opažanjima na Zemlji i Ptolemej  ga je zbog toga ismijavao. Naime, ako Zemlja kruži oko mirujućega Sunca, s vremenskim periodom kruženja od 365 dana, onda mi jurimo kroz prostor nevjerojatnom brzinom od 100 000 km/h, a da to nitko na Zemlji ne primjećuje. To je potpuno apsurdno, pa su i kopernikanci bili ismijavani. (Na jednoj od karikatura iz tog vremena dva smušena kopernikanca vertikalno iznad sebe ispaljuju topovsko tane i ne brinu se da će pasti na njihove glave, jer kada stigne do tla njih će već daleko odnijeti nevjerojatno brza Zemlja.)

Ipak, “ta puka matematička hipoteza”, kako je u svojem predgovoru Kopernikovu djelu naziva Osiander, dobro objašnjava retrogradna gibanja planeta, razlike u položajima nutarnjih i vanjskih planeta i mnoge druge nebeske fenomene. Možda naša opažanja na Zemlji treba uskladiti s matematiziranom astronomijom, a ne nju ismijavati i odbacivati zbog tih opažanja.

U Zvjezdanom glasniku (Sidereus nuncius) iz 1610. godine, Galileo izvještava da Mjesec nije savršena eterična kugla

Pravi pitagorejci više vjeruju svojim matematičkim teorijama nego svojim opažanjima. Za Galilea “trokuti, kvadrati, kružnice, sfere, konusi i piramide slova su kojima je ispisana knjiga prirode”. Galileo će stoga uvesti inercijsku fiziku koja matematičku astronomiju usklađuje s opažanjima na Zemlji i koja ispod površine tih opažanja otkriva dublju matematiziranu stvarnost idealnih čestica koje se bez utjecaja vanjskih sila jednoliko gibaju (a ne nužno miruju). Pomoću te dublje stvarnosti uspješno će rekonstruirati naša površinska opažanja. Aristotelova empirijska fizika Zemlje ustupit će mjesto jedinstvenoj matematičkoj fizici neba i Zemlje.

Po uzoru na paradigmatsku prirodnu znanost, fiziku, matematizirane su i ostale prirodne znanosti, pa se danas razina znanstvenosti gotovo poistovjećuje s razinom matematiziranosti. Naravno, prirodne znanosti iako matematizirane i dalje su empiričke, ali ne stoga što se u Aristotelovom i Baconovom smislu izvode iz opažanja nego stoga što se testiraju opažanjima. (Ta se razlika obično iskazuje oprekom empirijsko-eksperimentalno.)

Knjiga prirode ne leži pred nama širom otvorena. Ona pred nama leži zatvorena i moramo je uporno otvarati, ne bi li odgovorila na naša pitanja. Ruke koje je otvaraju naše su matematizirane prirodnoznanstvene teorije.

Po uzoru na paradigmatsku prirodnu znanost, fiziku, matematizirane su i ostale prirodne znanosti, pa se danas razina znanstvenosti gotovo poistovjećuje s razinom matematiziranosti

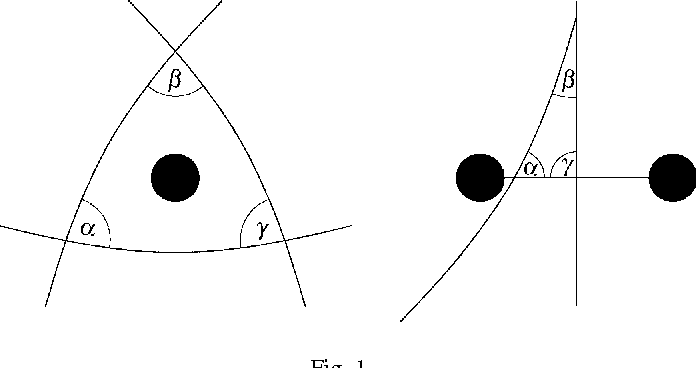
Ovo jedinstvo matematike i prirodnih znanosti s vremenom je ipak narušeno. Razvoj neeuklidske geometrije bio je jedan od važnih faktora. Sve je počelo u doba kasne antike s postavljanjem zahtjeva koje bi morali zadovoljavati nedokazani postulati i nedefinirani primitivni pojmovi Euklidovih Elemenata. Naime, prvi trebaju biti samorazumljivo istiniti, a drugi samorazumljivo smisleni. Peti Euklidov postulat o paralelama tu je loše prolazio, kao jedini kojem nedostaje samorazumljivost. Sam Euklid implicitno je priznao da je taj postulat problematičan, budući da u ranim dijelovima 1. knjige Elemenata što god može radi bez pozivanja na taj postulat. Počinje ga koristiti, jer mora, tek da bi dokazao teorem o zbroju kutova u trokutu.

Mnogi kasniji autori, od antičkih do modernih vremena, pokušavali su dokazati postulat o paralelama, no uspijevali su ga tek zamijeniti nekim ekvivalentnim postulatom, koji nije bio bitno očigledniji od onoga što je zamijenio. Najpoznatija od ovih ekvivalentnih alternativa, vjerojatno je svim učenicima poznat Playfairov postulat: kroz točku izvan pravca može se povući točno jedan pravac paralelan s tim pravcem. Neki autori, među kojima se osobito ističe Girolamo Saccheri, pokušavali su izvesti kontradikciju iz negacije postulata o paralelama i tako reductiom ad absurdum dokazati sam postulat.

Negacija Playfairove formulacije može se razbiti u dva dijela:

(1)  nema paralele kroz zadanu točku i

(2)  kroz zadanu točku postoje mnoge paralele.

Iz njih su izvedene mnoge posljedice koje danas znamo kao teoreme eliptičke geometrije (u kojoj je zbroj kutova u trokutu uvijek veći od dva prava kuta, a što je veći trokut veći je i višak) i hiperboličke geometrije (u kojoj je zbroj kutova u trokutu uvijek manji od dva prava kuta, a što je veći trokut veći je i manjak).

Saccherijevi napori da izvede kontradikciju iz (1) i (2) nisu uspijevali jer su i eliptična i hiperbolična geometrija konzistentne. Ta konzistentnost oba oblika neeuklidske geometrije na kraju je i strogo dokazana (pod pretpostavkom  konzistentnosti same euklidske geometrije) konstrukcijom modela obaju geometrija unutar euklidske geometrije. Eliptična geometrija modelirana je sfernom geometrijom (u kojoj je “ravnina” sfera, a “pravci” su velike kružnice „s identificiranim dijametralno suprotnim točkama“). Hiperbolična geometrija je modelirana Poincaréovim diskom (u kojem je “ravnina” područje unutar kruga, a “pravci” su oni lukovi kružnica koji su okomiti na granični krug). Prije nego što su dani ti strogi  dokazi konzistentnosti Janos Bolyai i Nikolaj Lobačevski bili su u nju toliko uvjereni da se nisu libili objaviti svoja djela o novoj hiperboličkoj geometriji.

Jedinstvo matematike i prirodnih znanosti narušeno je razvojem neeuklidske geometrije

Carl Friedrich Gauss, koji je na kocki imao veću reputaciju, svoje radove o neeuklidskim geometrijama nije objavio iz straha od sukoba s Kantovim filozofskim sljedbenicima. Iako konzistentnost neeuklidske geometrije zapravo potvrđuje pola Kantovog pogleda na Euklidsku geometriju kao sintetičku, a ne analitičku (što znači da se ona ne sastoji samo od logičnih posljedica definicija), upitna je druga polovina Kantovog pogleda na euklidsku geometriju, naime, njegova tvrdnja da je ona apriorna, a ne aposteriorna (što znači da se njeni principi ne izvode induktivno iz osjetilnog iskustva, nego su spoznatljivi čistim mišljenjem). Konzistentnost neeuklidske geometrije logički ne implicira da je euklidska geometrija aposteriorna, no čim su matematičari prihvatili konzistentnost neeuklidske geometrije, neki od njih počeli su propitivati ​​imaju li kantovci doista uvjerljivih osnova da tvrde da je euklidska geometrija apriorna.

Gauss je odbacio tvrdnju da je euklidska geometrija  apriorna tvrdeći da ona ima isti status kao i mehanika. To znači da je istinitost ili neistinitost njenih tvrdnji podložna empirijskom testu i o tome konačno trebaju odlučiti prirodoslovci, a ne matematičari. Na primjer, geodeti bi trebali izmjeriti je li suma kutova koji tvore tri planinska vrha 180 ° ili nije. Gauss je to i pokušao, iako je znao da neeuklidske geometrije impliciraju da je prostor lokalno euklidski pa njegov neeuklidski karakter možda eksperimentalno neće biti prepoznat jer trokuti koje mjerimo nisu dovoljno veliki (a ni mjerenja nisu dovoljno točna; Gauss je otac matematičke teorije grešaka).

Dakle, nijedna geometrijska teorija ne implicira empirijska predviđanja sama za sebe, bez ikakvih fizičkih hipoteza. Čak i predloženi geodetski eksperiment  pretpostavlja da svjetlost putuje po pravcima, što znači da uz geometriju uključuje i optiku, tj. elektromagnetsku teoriju (a kasnije se pokazalo da je geometrija isto tako neodvojiva od gravitacijske teorije).

Tako se pojavila distinkcija, implicitna već u Gaussovom stajalištu, između matematičkih geometrija i fizičke geometrije. Matematike je postala istraživanje raznih matematičkih ‘prostora’, euklidskih, neeuklidskih, četvero i više dimenzionalnih itd., a tek fizika treba odlučiti koji je od njih najprikladniji kao model prostora u kojem živimo. Posebno, vrijedi li postulat o paralelama u fizičkom prostoru nije stvar o kojoj trebaju odlučiti matematičari, to je pitanje za fizičare.

Fizika mora prosuditi koji je matematički prostor prikladan za modeliranje fizičkog prostora, ali jednako je važna spoznaja da matematički prostor koji nije primjeren model fizičkog prostora možda može poslužiti kao model nekog drugog fenomena. Na primjer, predstavljanje ekonomskih podataka točkama u višedimenzionalnom Euklidskom prostoru može imati sasvim nepredviđene primjene u društvenim znanostima.

Matematičar ne koristi hipotezu empirijskog znanstvenika da promatrani matematički sustav dobro modelira neki poznati prirodni ili društveni fenomen. Ništa se ne smije pretpostaviti u dokazima matematičkog sustava samo zato što se čini da je odgovarajuća tvrdnja točna o empirijskom fenomenu koji on modelira

Tako dolazi do nove podjele rada. Matematičari proučavaju mnoge matematičke sustave. Empirijski znanstvenici predlažu hipotezu da neki od tih sustava modelira određeni prirodni ili društveni fenomen, a zatim primjenjuju matematičke rezultate o tom sustavu kako bi došli do empirijskih predviđanja. Ako eksperimenti pokažu da su ta predviđanja netočna, model se mora modificirati ili čak napustiti i tražiti neki drugi model. No, matematički rezultati o matematički istraženom sustavu ostaju i možda će se jednog dana upotrijebiti u modeliranju nečeg drugog.

Ovaj novi način rada jasno pretpostavlja da matematičar u izvođenju teorema, ni u jednom trenutku ne koristi hipotezu empirijskog znanstvenika da promatrani matematički sustav dobro modelira neki poznati prirodni ili društveni fenomen. Ništa se ne smije pretpostaviti u dokazima matematičkog sustava samo zato što se čini da je odgovarajuća tvrdnja točna o empirijskom fenomenu koji on modelira – ako želimo biti sigurni da matematički rezultat vrijedi čak i ako se ta empirijska tvrdnja pokaže netočnom. Posebno, prostorno-vremenske intuicije ne smiju biti uključene u dokaze. Ako matematika i empirijska znanost žele raditi zajedno, uz opisanu podjelu rada, prihvatljivi su samo rigorozni dokazi koji svaki teorem izvode iz eksplicitnih pretpostavki o matematičkom sustavu o kojem je riječ.

Tako je u drugoj polovici 19. stoljeća počela rigorizacija matematike, koja je završila njenim utemeljenjem u teoriji skupova, a početkom 20. stoljeća u aksiomatiziranoj teoriji skupova ZFC (proširenoj, ako je to potrebno, aksiomima o postojanju velikih kardinalnih brojeva). Što to zapravo znači? Najjednostavnije, da se svi matematički pojmovi mogu definirati u toj teoriji te da se iz njenih aksioma mogu izvesti svi matematički teoremi. Nešto detaljnije, da se matematički objekti (poput brojeva, funkcija i sl.) mogu definirati kao određeni skupovi, te da se matematički teoremi (poput osnovnog teorema algebre, analize i sl.) tada mogu promatrati kao izjave o skupovima koje su dokazive iz aksioma teorije skupova. Napomenimo još da je to uranjanje matematike u teoriju skupova danas toliko dobro poznato da često zaboravljamo koliko je ono zapanjujuće.

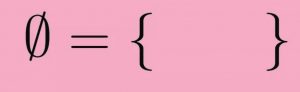
No, u kojem smislu to uranjanje matematike u teoriju skupova utemeljuje matematiku?

Neki idu tako daleko da uranjanje matematike u teoriju skupova drže njenim ontološkim utemeljenjem. Oni smatraju da je predstavljanje danog matematičkog objekta određenim skupom zapravo otkriće njegovog istinskog identiteta. Benacerraf je upozorio da to ne može biti točno jer, na primjer, Zermelo prirodne brojeve skupovno definira kao ∅, {∅}, {{∅}},. . . , a von Neumann kao ∅, {∅}, {∅, {∅}},. . ., i nema principijelnog razloga da se jedna definicija preferira u odnosu na drugu (postoje praktični razlozi za preferiranje von Neumannovih ordinalnih brojeva, npr. oni se lako generaliziraju na transfinitne ordinalne brojeve, ali takve stvari nisu pokazatelj toga ‘što su brojevi zapravo’ – iako u ovom posebnom slučaju osobno imam neke rezerve, usp. What are numbers.

Praksa teorije skupova puna je ovakvih proizvoljnih izbora, poput definicije uređenog para na način Kuratowskog pa je važno upozoriti da su to definicije matematičkih pojmova u teoriji skupova, a ne otkrića identiteta tih pojmova. Iako matematičari u takvim situacijama govore o identifikaciji, npr. realnih brojeva s nizovima nula i jedinica, oni u takvim slučajevima ‘identifikaciju’ shvaćaju kao ‘vjernu reprezentaciju’. Naravno, ključno je pitanje što je ‘vjerna reprezentacija’. Za slučaj uređenih parova to je lako: dva uređena para trebaju biti jednaki ako su im međusobno jednake prve i druge komponente. Slučaj realnih brojeva zahtjevniji je: skup realnih brojeva sa svojim operacijama treba zadovoljiti aksiome potpunog uređenog polja, za koje je prethodno dokazano da su kategorični.

Dakle, uranjanje matematike u teoriju skupova ne daju nikakve duboke ontološke informacije o prirodi matematičkih objekata, uređenih parova, realnih brojeva i sl., niti je to uranjanje tome namijenjeno.

Mnogi ‘redukciju’ klasične matematike na teoriju skupova vide kao nastavak i bar djelomično ostvarenje Fregeovog logicizma. Fregeov projekt bio je epistemološki: ako se matematika može svesti na logiku, tada se matematička spoznaja svodi na logičku (što pobija Kantovu tezu da je ona sintetička i apriorna). Pod pretpostavkom da je logička spoznaja temeljnija od matematičke to je jasni epistemološki dobitak. Kada se Fregeov logicizam pokazao nekonzistentnim teorija skupova zauzela je njegovo mjesto, ali epistemološka analiza je sačuvana: za matematičke teoreme znamo da su istiniti jer znamo da logički slijede iz aksioma teorije skupova za koje pak znamo da su istiniti. Tako je problem spoznavanja matematičkih istina sveden na problem spoznavanja istinitosti aksioma teorije skupova i valjanosti logičkih dedukcija.

Naravno, već je Russell upozorio (a to zna i svaki matematičar koji je dokazao neki bar donekle složeniji teorem) da naša matematička znanja ne izviru logičkim slijedom iz aksioma, nego se ti aksiomatski sljedovi izgrađuju naknadno, kada je već skupljen veliki fond matematičkih znanja. Dakle, redukcija na teoriju skupova možda je logička, ali sigurno nije epistemološka.

Tako su razmišljali Zermelo i drugi začinjavci, kada su teoriju skupova držali onom granom matematike čiji je zadatak matematički istražiti temeljne pojmove ‘broj’, ‘uređaj’, ‘funkcija’ i sl. te na taj način uspostaviti logičke temelje čitave aritmetike i analize. Naknadni razvoj proširio je doseg teorije skupova, u tom smislu, na cijelu klasičnu matematiku. Teorija skupova time je jasno pokazala da je matematika jedinstvena znanost s jedinstvenim predmetom i metodologijom. I ranije su matematičari uspješno povezivali naizgled daleka područja (npr. geometriju, kompleksnu aritmetiku i teoriju funkcija, što je amblemski predstavljeno slavnom formulom e^iπ = -1), ali teorija skupova je tome dala jasan i sveobuhvatan matematički okvir.

Tako je postalo moguće da nešto kažete pa i dokažete o cjelokupnoj klasičnoj matematici. Kada ste je skupili u jedan paket, teoriju skupova, mogli ste npr. postaviti pitanje njezine konzistentnosti, što je i učinila Hilbertova škola.  Naravno, Gödel se pobrinuo, svojim teoremima nepotpunosti, da projekt ne uspije onako kako su se nadali Hilbert i njegovi sljedbenici, ali činjenica je da ni Gödelov rezultat (klasična matematika ne može dokazati vlastitu konzistentnost – ako jest konzistentna) nije moguć bez uranjanja cijele klasične matematike u teoriju skupova ili neki ekvivalentni okvir.

Otkako je Gödel dokazao nedokazivost konzistentnosti klasične matematike (u njenom skupovno-teorijski formaliziranom obliku) dokazana je nedokazivost i mnogih drugih specifično matematičkih tvrdnji; u teoriji brojeva, analizi, algebri, beskonačnoj kombinatorici, teoriji skupova itd. Mnoge od njih moguće je dokazati u teoriji skupova proširenoj nekim aksiomom o postojanju skupova s velikim kardinalnim brojem (ZFC + ) čime se, katkada na veoma neočekivane načine, proširio „sveobuhvatni matematički okvir“. Naime, dosta je neočekivano (iako smo danas na to već navikli) da za dokaz neke tvrdnje o prirodnim brojevima, koji čine najmanji beskonačni skup, katkada trebamo pretpostaviti postojanje enormno velikih beskonačnih skupova

Ako prihvatimo da dokazivanja ovakvih općih tvrdnji o klasičnoj matematici jest nešto za nju ‘temeljno’, onda ovdje sigurno nalazimo temeljnu ulogu teorija skupova.

Klasična matematika ne može dokazati vlastitu konzistentnost – ako jest konzistentna. Kurt Gödel

No, to nije sve. Već u Dedekinda nalazimo još jednu temeljnu ulogu teorije skupova: „pronalaženje čisto aritmetičkog i savršeno strogog utemeljenja infinitezimalnog računa“. To Dedekind ostvaruje svojom teorijom realnih brojeva kao rezova u području racionalnih brojeva, koja je izgrađena sredstvima teorije skupova.

Na prvi pogled ovo može izgledati kao samo još jedan primjer teoretske redukcije o kojoj smo već govorili, ali zapravo se radi o još nečemu. Tu nemamo samo matematičke objekte (uređene parove ili realne brojeve) koje ‘identificiramo’ sa skupovima koji ih ‘vjerno reprezentiraju’. U ovom slučaju prilično nejasna slika kontinuuma (koja je matematičarima, ipak, stoljećima dobro služila za razvoj nevjerojatno uspješnog infinitezimalnog računa) zamijenjena je pojmovima koji su dovoljno precizni za ono što Dedekind traži: stroge dokaze temeljnih teorema.

Dakle, Dedekindova teorija nije samo skupovno-teorijski surogat, osmišljen da ‘vjerno reprezentira’, nego je teoretsko poboljšanje. Skupovno-teorijsko zamjena nepreciznog pojma preciznim. To je još jedna utemeljujuća uloga teorije skupova: eksplikacija nedovoljno jasnih matematičkih pojmova.

Jedan od najranijih primjera takve eksplikacije je von Staudtovo rješenje problema razumijevanja idealnih elemenata u projektivnoj geometriji. Na primjer, točke u beskonačnosti u kojima se ‘sijeku’ međusobno paralelni pravci von Staudt identificira sa skupom tih paralelnih pravaca, a za točku u beskonačnosti kaže da pripada nekom pravcu ako on pripada skupu s kojim je ta točka identificirana. Na ovaj način, von Staudt je uspio od ne-problematičnog materijala (običnih pravaca) izgraditi surogate za do tada problematične objekte (poput točaka u beskonačnosti) i redefinirati relevantne relacije kako bi potvrdio postojeću teoriju.

Formalno izvođenje u teoriji skupova  služi i kao zajednički standard onoga što se smatra rigoroznom matematikom

S vremenom je postalo jasno da su alati potrebni za ovaj proces gradnje (alati koje je von Staudt, kao kasnije Frege, smatrao logičkim) zapravo alati teorije skupova. Ova zapanjujuća činjenica, da se metode von Staudta i ostalih svode na svega nekoliko principa koje su koristili rani teoretičari skupova i koje je kasnije kodificirao Zermelo, jest ono što je na kraju omogućilo redukciju klasične matematike na teoriju skupova u gore opisanom smislu.

I na kraju, formalno izvođenje u teoriji skupova (barem u načelu) služi i kao zajednički standard onoga što se smatra rigoroznom matematikom. Zamršena i produktivna isprepletenost mnogih grana moderne matematike implicira da više nije dovoljno svaku pojedinu granu rigorozno zasnivati samu za sebe. Kako bi se zajamčilo da strogost neće biti ugrožena u procesu prijenosa rezultata i metoda iz jedne grane u drugu, bitno je da one budu kompatibilne. Jedini očiti način da se osigura ta kompatibilnost jest da se sve grane izvedu iz objedinjenog polazišta. Univerzum teorije skupova taj je (već deklarirani) matematički okvir, a izvodi iz njegove ZFC aksiomatizacije predstavljaju standard dokaza u matematici. Na primjer, prestižni Annals of Mathematics traži da se hipoteze koje izlaze van okvira ZFC-a (poput postojanja velikih kardinalnih brojeva) eksplicitno navode, dok se one unutar ZFC-a prešutno pretpostavljaju. To zapravo znači da je ZFC njihov službeni standard dokazivanja (naravno dokazi se ne ispisuju u ZFC formalizmu, ali se podrazumijeva da bi to bilo moguće napraviti).

Možemo zaključiti: teorija skupova utemeljuje matematiku kao njen sveobuhvatni okvir, kao mjesto eksplikacije matematičkih pojmova i kao standard rigoroznog dokazivanja.

Tu se zatvara krug razvoja matematike, od njenog konstituiranja kao apstraktne znanosti primjerene samo razumijevanju postojanog eteričnog neba, preko njenog uvlačenja  u same temelje znanstvenog razumijevanja nepostojane materije, do njenog konačnog razumijevanja kao znanosti o apstraktnim sustavima koji katkada dobro modeliraju konkretni materijalni svijet i koji su utemeljeni u teoriji skupova.