Logička korektnost, potpunost i kompaktnost. Gentzenov IF-sustav i Bethova semantička stabla

U trećem nastavku serijala o logici, Zvonimir Šikić fokusira se na pojmove logičke korektnosti, potpunosti i kompaktnosti, te predstavlja pravila i definicije za konstrukciju Bethovih semantičkih stabala.

• Naslovna fotografija: Nizozemski filozof i logičar Evert Willem Beth (lijevo) i njemački matematičar i logičar Gerhard Gentzen (desno) (CC0)

• Prethodni članci u seriji: Zaključivanje u prirodnom i artificijelnom jeziku. Od Aristotela prema Fregeu, Logika sudova. Kondicionali, bikondicionali i implikacije

1. Bethova semantička stabla

Analiza istinosnih vrijednosti neke forme, kao i njezina tablica istinitosti, daje iscrpnu informaciju o vrijednosti istinitosti te forme u svakoj interpretaciji. Bethova metoda semantičkih stabala nije u tom smislu iscrpna. Tom metodom pokušavamo naći bar jednu interpretaciju u kojoj forma ima zadanu vrijednost ili, nešto općenitije, u kojoj sve forme iz skupa Γ imaju vrijednost ⊤, a sve forme iz skupa Δ vrijednost ⊥. To znači da pokušavamo naći bar jednu interpretaciju koja dokazuje da Γ ⊭ Δ.

Prije definiranja metode ilustrirat ćemo je s par primjera. Pokušajmo, dakle, naći interpretaciju koja \(\scriptsize P \rightarrow Q\) vrednuje s ⊤ i \(\scriptsize \overline{P}Q\) vrednuje s ⊥. To je interpretacija koja dokazuje da \(\scriptsize P \to Q \not\models \overline{P}Q \). Polazimo od zahtjeva

­­

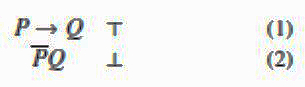
Prvi zahtjev, \(\scriptsize P \rightarrow Q\) ⊤, može se ostvariti na dva načina, tako da \(\scriptsize P\) bude ⊥ ili da \(\scriptsize Q\) bude ⊤:

­­

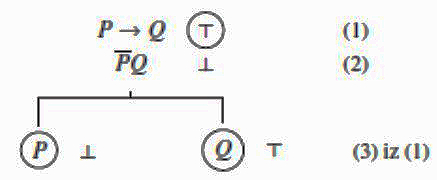
To da smo zahtjev \(\scriptsize P \rightarrow Q\) ⊤ analizirali označili smo zaokruživanjem zahtijevane vrijednosti. Dvije alternative za ostvarenje tog zahtjeva postale su dvije grane našeg semantičkog stabla. Zaokruživanje atoma \(\scriptsize P\) i \(\scriptsize Q\) znači da su to zahtjevi koji se dalje ne mogu analizirati i koji konačno zahtijevaju da se \(\scriptsize P\) interpretira sa ⊥ i \(\scriptsize Q\) sa ⊤.

Ostao je još zahtjev \(\scriptsize \overline{P}Q\) ⊥, koji se može ostvariti tako da \(\scriptsize \overline{P}\)  bude ⊥ ili da \(\scriptsize Q\) bude ⊥:

­­

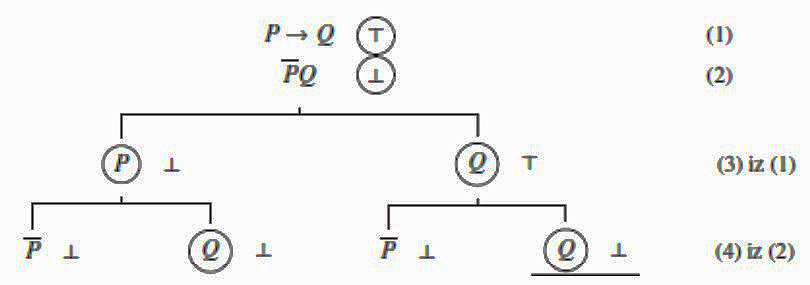
Zahtjev \(\scriptsize \overline{P}Q\) ⊥ nalazi se na obje grane, pa se one obje razvijaju u po dvije alternative koje ga ostvaruju. Tako smo dobili ukupno četiri alternative (tj. četiri grane) za ispunjenje početnih zahtjeva. Četvrta alternativa (tj. četvrta grana) sadrži kontradiktorne zahtjeve da \(\scriptsize Q\) bude ⊤ i ⊥. Ona nije moguća što označavamo crtom ispod te grane i tu granu zovemo zatvorenom.

Na kraju je ostao još jedan zahtjev, \(\scriptsize \overline{P}\) ⊥, koji se ostvaruje samo na jedan način, \(\scriptsize P\)  ⊤:

­­

Stablo je potpuno razvijeno jer više nema zahtjeva koje bi trebalo ispuniti (svi su zahtjevi zaokruženi). Od četiri grane dvije su se zatvorile, jer su na njima kontradiktorni zahtjevi. No, dvije su ostale otvorene i sa svake od njih možemo očitati interpretaciju koja ispunjava početne zahtjeve, \(\scriptsize P \rightarrow Q\) ⊤ i \(\scriptsize \overline{P}Q\) ⊥. To su (P,Q)=(⊥,⊥) s treć grane i (P,Q)=(⊤,⊤) s druge. Svaka od njih dokazuje da \(\scriptsize P \to Q \not\models \overline{P}Q \).

Sljedeći primjer u kojem nećemo detaljno obrazlagati svaki korak, ilustrira situaciju u kojoj nije moguće ispuniti početne zahtjeve koji bi dokazali da Γ ⊭ Δ. No, time je dokazano da Γ ⊨ Δ. Tako dokazujemo da \(\scriptsize -(P \overline{Q}) \models \overline{P} \lor Q\):

:

­­

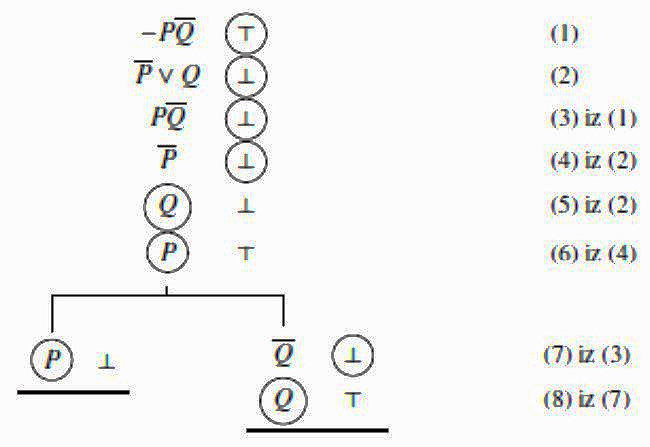
Sve su se grane zatvorile. Dakle, nema interpretacije koja bi dokazala \(\scriptsize -(P \overline{Q}) \not\models \overline{P} \lor Q\). To znači da \(\scriptsize -(P \overline{Q}) \models \overline{P} \lor Q\).

Upoznavši se preko ovih primjera s osnovnom idejom semantičkih stabala, sada ih možemo i precizno definirati. Najprije ćemo formulirati pravila kojima se koristimo pri izgradnji semantičkih stabala. Svaki IF–veznik ima jedno pravilo koje određuje kad je forma izgrađena pomoću tog veznika istinita i drugo koje određuje kada je ona neistinita.

IF-PRAVILA ZA IZGRADNJU SEMANTIČKOG STABLA

­­

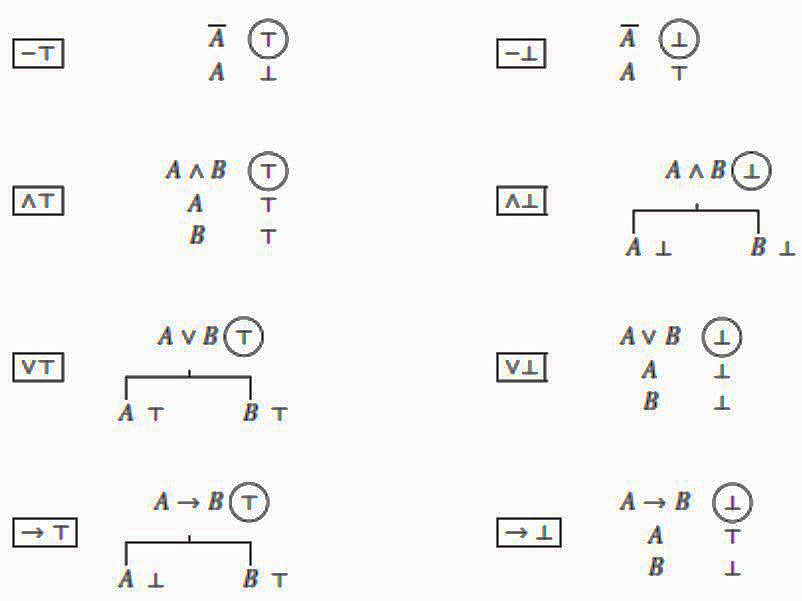
Pravila možemo izvesti i za bilo koji drugi IF–veznik, iako smo se mi ograničili na standardni skup {-, ∧ , ∨, →}. Na primjer, razmotrimo veznik ↚  zadan tablicom:

­­

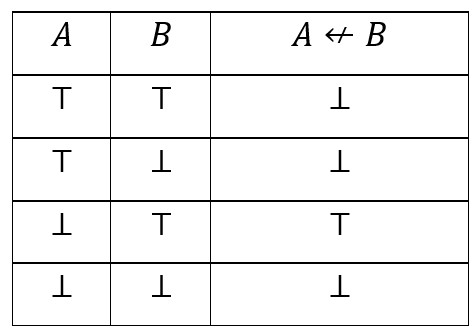
Iz tablice vidimo da je jedini način da A \(\small \not\leftarrow\) B bude ⊤ taj da A bude ⊥ i da B bude ⊤. To jednoznačno određuje (\(\small \not\leftarrow\) ⊤) pravilo. S druge strane, postoje tri alternative u kojima je A \(\small \not\leftarrow\) B ⊥ pa bi mogli očekivati da (\(\small \not\leftarrow\) ⊥) vodi na tri grane (što je sasvim u redu). No, te tri alternative mogu se svesti na dvije: A je ⊤ ili je B ⊥. Dakle, pravila za \(\small \not\leftarrow\) su:

­­

Dalje se time nećemo baviti, ali očito je kako se za svaki IF–veznik mogu formulirati odgovarajuća pravila. Sada možemo definirati i pojam semantičkog stabla za Γ ⊭ Δ.

DEFINICIJA BETHOVOG SEMANTIČKOG STABLA

Formule oblika A ⊤ ili A ⊥, gdje je A forma, zovemo označenim formama ili zahtjevima. Ako je Γ skup formi onda s Γ ⊤ i Γ⊥ označavamo odgovarajuće skupove označenih formi (forme u Γ ⊤ označene su s ⊤, one u Γ⊥ označene su s ⊥).

Bethovo semantičko stablo za Γ ⊭ Δ je stablo koje počinje nizom svih zahtjeva iz Γ ⊤ i Δ ⊥ (pretpostavljamo da su Γ i Δ konačni) i u kojem je svaki sljedeći zahtjev Z posljedica primjene semantičkog pravila na neki zahtjev koji u stablu prethodi zahtjevu Z.

Grana je potpuno razvijena ako su svi njeni zahtjevi zaokruženi (bilo forme, bilo njihove oznake). Grana je zatvorena ako je podvučenom crtom, tj. ako se na njoj pojavljuju kontradiktorni zahtjevi A ⊤ i A ⊥.

Grana je završena ako je potpuno razvijena ili zatvorena.

Stablo je završeno ako su mu sve grane završene. Stablo je zatvoreno ako su mu sve grane zatvorene.

Evo još nekoliko primjera. Počnimo sa semantičkim stablom za \(\scriptsize P \lor \overline{R}, Q \to R \not\models P \lor \overline{Q}\).

­­

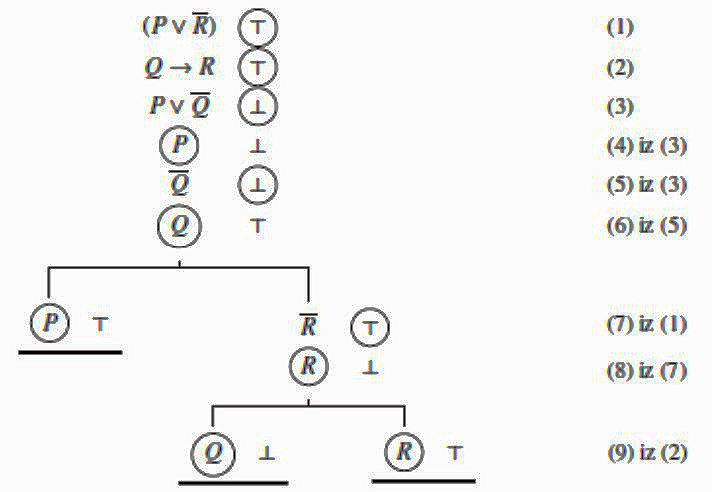
Stablo se zatvorilo (tj. sve su se njegove grane zatvorile). To znači da nema interpretacije koja bi potvrdila da \(\scriptsize P \lor \overline{R}, Q \to R \not\models P \lor \overline{Q}\). Dakle, \(\scriptsize P \lor \overline{R}, Q \to R \models P \lor \overline{Q}\).

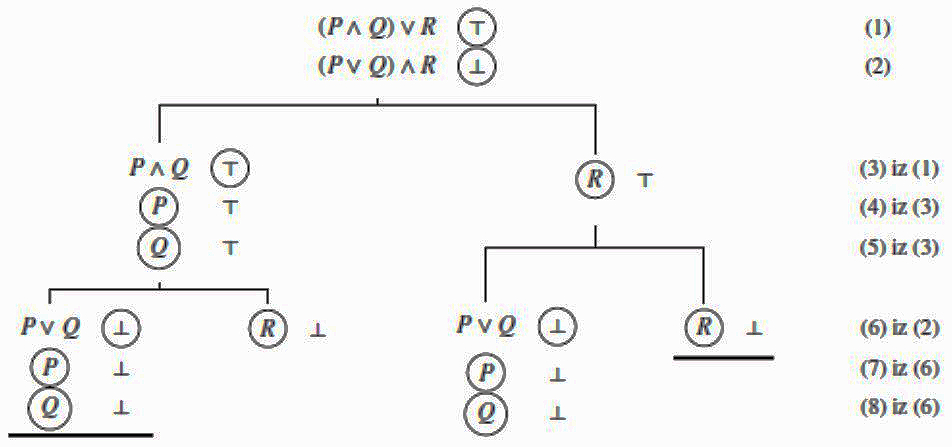
Sljedeći je primjer semantičko stablo za \(\scriptsize (P \land Q) \lor R \not\models (P \lor Q) \land R\).

­­

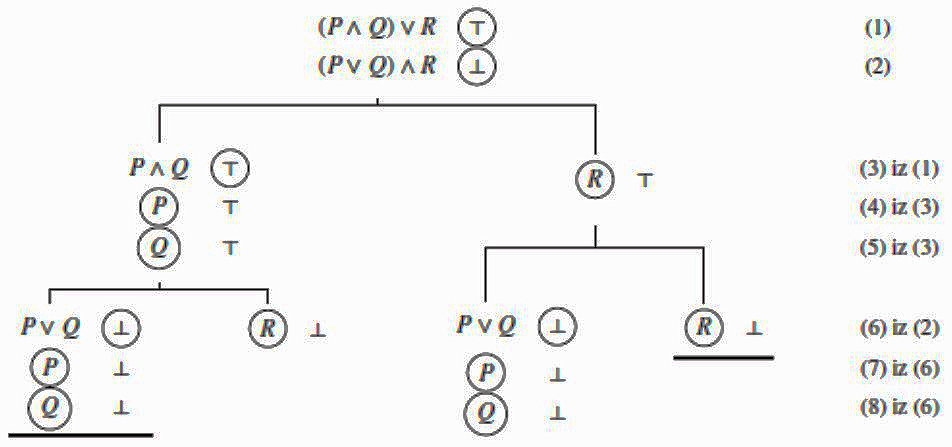
Stablo je završeno (svi zahtjevi su zaokruženi) ali nije zatvoreno. Otvorene su dvije grane i s njih možemo očitati interpretacije koje potvrđuju \(\scriptsize (P \land Q) \lor R \not\models (P \lor Q) \land R\). To su \(\scriptsize (P, Q, R) = (\top, \top, \bot)\) i \(\scriptsize (P, Q, R) = (\bot, \bot, \top)\).

Metoda semantičkih stabala, za svaki konačni Γ i Δ, daje odgovor na pitanje je li Γ ⊨ Δ ili je Γ ⊭ Δ. Naime, izgradnja semantičkog IF–stabla, za konačne Γ i Δ, sigurno završava u konačno mnogo koraka (jer Γ i Δ sadrže konačno mnogo IF–veznika, dakle i zahtijeva). No, tada preostaju samo dvije mogućnosti. Sve su grane tog stabla zatvorene, pa je dokazano da Γ ⊨ Δ, ili je bar jedna grana otvorena pa je dokazano da Γ ⊭ Δ (jer s te grane možemo očitati interpretaciju koja to dokazuje).

Dakle, metoda semantičkih stabala je postupak odluke za Γ ⊨ Δ. Njezina glavna prednost je da se ona lako poopćuje i na logiku kvantificiranih formi (iako tako poopćena više neće biti postupak odluke za Γ ⊨ Δ).

2. Korektnost, potpunost i kompaktnost

U drugom poglavlju uveli smo Gentzenov sekventni IF–sustav u kojem se dokazuju (generalizirane) IF-implikacije. Za njegove dokaze kažemo da su sintaktički, jer se pravila mogu primjenjivati čisto mehanički, uzimajući u obzir samo sintaktičku građu formi na koje se primjenjuju, a ne i njihovu semantiku (da bi se to naglasilo sekvente takvih sustava dokazivanja najčešće se označavaju se s ⊢, a na s ⊨).

DEFINICIJA KOREKTNOSTI

Sustav dokazivanja je korektan ako svaka u njemu dokaziva implikacija jest implikacija.

Gentzenov sekventni IF-sustav je korektan, jer sva njegova pravila čuvaju relaciju ⊨ . Tako smo ih uveli u drugom poglavlju.

DEFINICIJA POTPUNOSTI

Sustav dokazivanja je potpun ako je u njemu dokaziva svaka implikacija.

Dokaz potpunosti Gentzenovog IF-sustava provest ćemo koristeći se jednom čisto notacijskom preformulacijom metode semantičkih stabala. Izgradnja semantičkog stabla za Γ⊭Δ počinje s granom na kojoj su formule iz Γ označene s ⊤, a one iz Δ s ⊥. Tu ćemo granu u novoj notaciji zapisati jednostavno kao Γ⊭Δ.

Na primjer, početak semantičkog stabla za \(\scriptsize – (P \land \overline{Q}) \not\models \overline{P} \lor Q\) u staroj notaciji je prikazan lijevo, a u novoj desno:

­­

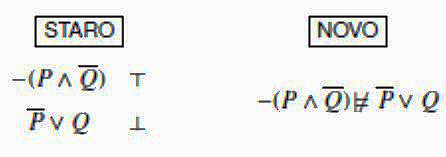
Izgradnja stabla se nastavlja primjenom semantičkih IF–pravila za izgradnju stabla. Ta pravila u staroj notaciji navodimo lijevo, a u novoj desno:

­­

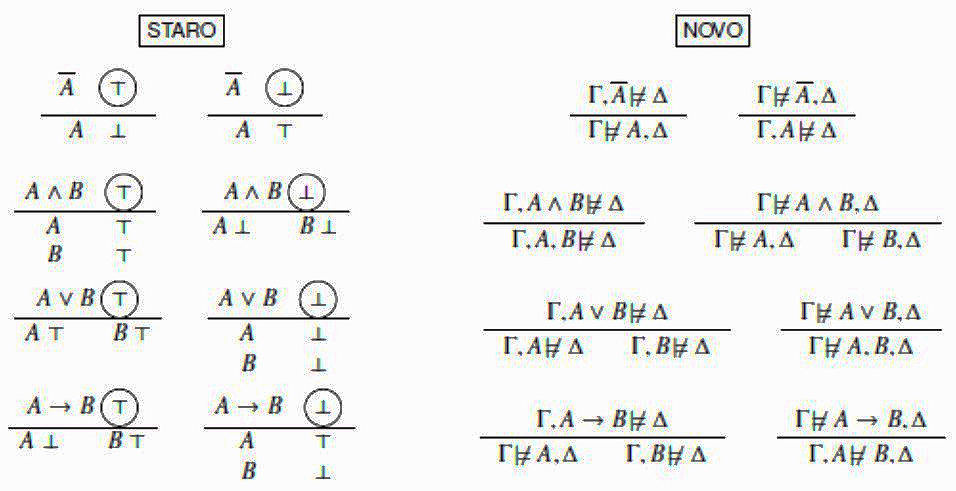
Dakle, u našem primjeru, u obje notacije, izgradnja semantičkog stabla za \(\scriptsize – (P \land \overline{Q}) \not\models \overline{P} \lor Q\) nastavlja se primjenom tih pravila na sljedeći način.

­­

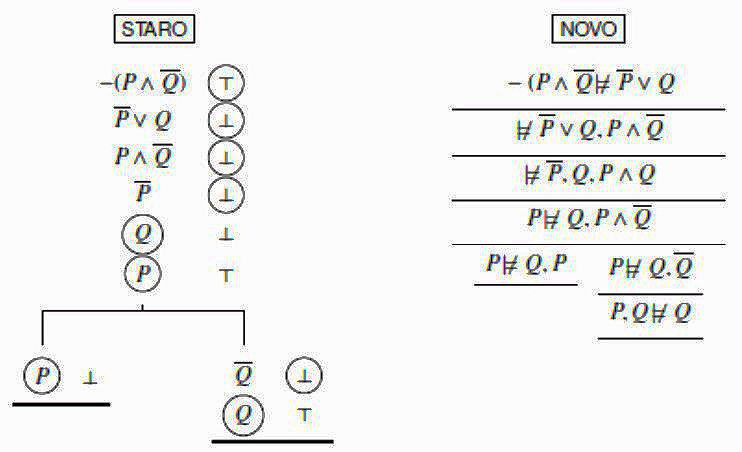
U svakoj fazi izgradnje stabala u “novim” se sekventama pojavljuju one forme čije su oznake na odgovarajućim “starim” granama nezaokružene. Najvažnije je uočiti da su semantička IF–pravila za izgradnju stabla ekvivalentna Gentzenovim sekventnim pravilima. Na primjer, pravilom

­­

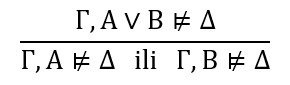
tvrdi se: ako Γ, A ∨ B ⊭ Δ onda Γ, A ⊭ Δ ili Γ, B ⊭ Δ. Tome je ekvivalentno: ako Γ, A ⊨ Δ i Γ, B ⊨ Δ onda Γ, A ∨ B ⊨ Δ. No, to je Gentzenovo pravilo

­­

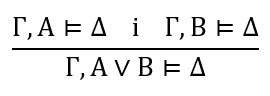
Isto vrijedi za ostala pravila. Dakle, semantičko stablo za \(\scriptsize – (P \land \overline{Q}) \not\models \overline{P} \lor Q\) u novoj notaciji i u obrnutom smjeru zapravo je Gentzenov dokaz sekvente \(\scriptsize – (P \land \overline{Q}) \not\models \overline{P} \lor Q\).

Sada je jasno kako možemo dokazati potpunost Gentzenovog sustava. Pretpostavimo da Γ ⊨ Δ. U tom slučaju izgradnja semantičkog stabla za Γ ⊭ Δ završava zatvaranjem svih njegovih grana. U novoj notaciji, grane se zatvaraju ako završavaju sekventama “preklapajućeg” oblika Θ, A ⊭ A, Φ. Iz prethodno objašnjene veze Gentzenovih i semantičkih IF–pravila slijedi da je to stablo, čitano u obrnutom smjeru, dokaz od Γ ⊨ Δ u Gentzenovom sustavu.

TEOREM O POTPUNOSTI I KOREKTNOSTI GENTZENOVOG IF-SUSTAVA

Gentzenov sekventni IF-sustav je potpun i korektan, tj. u njemu je implikacija dokaziva akko zaista jest implikacija.

Zapravo smo dokazali i nešto više, jer se u zatvorenim semantičkim stablima čitanim „naopako” nikada ne pojavljuju ni rez ni slabljenje. To znači da je Gentzenov sustav potpun čak i bez reza i slabljenja, tj. rez i slabljenje eliminabilni su iz Gentzenovog sustava. (Gentzen je teorem o eliminaciji reza dokazao sintaktički, ne pozivajući se na potpunost. To je kombinatorno dosta složen dokaz.)

U slučaju da su Γ i Δ konačni skupovi IF–formi, metoda semantičkih stabala je postupak odluke za Γ ⊨ Δ. U slučaju da su Γ ili Δ beskonačni nije neposredno jasno postoji li postupak odluke za Γ ⊨ Δ. Najjednostavnije bi bilo da je relacija ⊨ kompaktna (finitna).

DEFINICIJA KOMPAKTNOSTI (FINITNOSTI) RELACIJE ⊨

Ako Γ ⊨ Δ onda postoje konačni Γ’ ⊆ Γ i Δ’ ⊆ Δ takvi da Γ’ ⊨ Δ’.

Metodu semantičkih stabala možemo modificirati tako da bude primjenjiva na beskonačne sekvente Γ ⊨ Δ i tada možemo dokazati kompaktnost relacije ⊨. Modificirana metoda se za …, A₃, A₂, A₁ ⊭ B₁, B₂, B₃, … sastoji se od (potencijalno) beskonačno mnogo koraka.

1. korak

Polazeći od A₁⊤ izgradimo završeno stablo za taj zahtjev.

2. korak

Na kraju svih otvorenih grana dobivenih u prethodnom koraku dopišemo zahtjev B₁ ⊥ pa polazeći od novih zahtjeva izgradimo završeno stablo.

3. korak

Na kraju svih otvorenih grana dobivenih u prethodnom koraku dopišemo zahtjev A₂, ⊤ pa polazeći od novih zahtjeva izgradimo završeno stablo.

I tako dalje…

Postupak će stati ako se u nekom koraku sve grane zatvore, ili neće nikada stati ako u svakom koraku bar jedna grana ostane otvorena. U prvom slučaju stablo sadrži samo konačno mnogo početnih formula A_n, … A₂, A₁, B₁, B₂, …, B_m. Za njih vrijedi A_n, … A₂, A₁ ⊭ B₁, B₂, …, B_m, jer je stablo zatvoreno. U drugom slučaju stablo je beskonačno, pa ima bar jednu beskonačnu granu. Prema konstrukciji stabla na beskonačnoj grani pojavljuju se sve početne formule …, A₃, A₂, A₁, B₁, B₂, B₃, … i svi atomi od kojih su one izgrađene. Interpretacija u kojoj ti atomi imaju vrijednost s kojom su na toj grani označeni pridaje i ostalim formama na toj grani točno onu vrijednost s kojom su one označene. Posebno A₁, A₂, A₃, … primaju vrijednost ⊤, a B₁, B₂, B₃, .. primaju vrijednost ⊥. No to znači da …, A₃, A₂, A₁ ⊭ B₁, B₂, B₃, … .

Rezimirajmo, metoda semantičkih stabala za Γ⊭Δ s beskonačno mnogo formula:

1. Stane u konačno mnogo koraka i tada za konačne Γ’ ⊆ Γ i Δ’ ⊆ Δ imamo Γ’ ⊨ Δ’.
2. Ne stane u konačno mnogo koraka, tj. generira beskonačno stablo, i tada Γ ⊭ Δ.

Odavde odmah slijedi kompaktnost relacije ⊨. Naime, ako Γ ⊨ Δ onda 2. slučaj ne može nastupiti, pa postoje konačni Γ’ ⊆ Γ i Δ’ ⊆ Δ takvi da Γ’ ⊨ Δ’ .

TEOREM O KOMPAKTNOSTI (FINITNOSTI) IF-IMPLIKACIJE

Relacija ⊨ definirana među proizvoljnim skupovima IF–formi je kompaktna (finitna).

Kompaktnost IF–logike (a vidjet ćemo da ona vrijedi i za kvantifikacijsku logiku) zapravo je iznenađujuća, jer je vrlo lako naći jednostavne implikacije s beskonačno mnogo premisa koje ne vrijede ako se ograničimo na (bilo koji) konačni podskup tih premisa. Na primjer, beskonačno mnogo premisa a ≠ 0, a ≠ 1, a ≠ 2 … implicira konkluziju a ∉ \(\scriptsize \mathbb{N}\):

­­

Međutim, nijedan konačni podskup navedenih premisa ne implicira a ∉ \(\scriptsize \mathbb{N}\). To znači da implikacija …a≠2, a≠1, a≠0 ⊨ a ∉ \(\scriptsize \mathbb{N}\) ne slijedi iz istinosno funkcionalne (ili kvantifikacijske) građe premisa a ≠ i i konkluzije a ∉ \(\scriptsize \mathbb{N}\) . (Ta implikacija slijedi iz svojstva indukcije koje je temeljno svojstvo skupa prirodnih brojeva \(\scriptsize \mathbb{N}\).)

Upozorimo na kraju da modificirana metoda semantičkih stabala nije postupak odluke za beskonačne Γ ⊨ Δ. Naime, ako postupak stane u nekom koraku onda imamo odluku u tom koraku, tj. znamo da Γ ⊨ Δ. No, ako postupak ne staje, ne znamo je li to zato što nismo napravili dovoljan broj koraka ili zato što nikada ni neće stati (jer Γ ⊭ Δ).

Modificirana metoda je pozitivni test za Γ ⊨ Δ. Naime, ako vrijedi Γ ⊨ Δ test to i dokazuje (u konačno mnogo koraka). Ona nije negativni test za Γ ⊨ Δ. Naime, ako Γ ⊭ Δ test to ne dokazuje (u konačno mnogo koraka). Biti test odluke za neko svojstvo zapravo znači biti i pozitivan i negativan test za to svojstvo.