Logika predikata. Potpunost i korektnost Gentzenovog sekventnog Q-sustava

U 8. nastavku serijala o logici, Zvonimir Šikić se bavi interpretacijama kvantificiranih formi, kroz koje one dobivaju svoje značenje. Korak po korak uvodi relacijske strukture i pojam istinitosti forme u strukturi, te preko generalizirane implikacije i Bethovih semantičkih stabala dolazi do potpunosti Gentzenovog sekventnog Q-sustava za logiku predikata.

• Naslovna fotografija: Gerhard Gentzen crta po ploči. (Midjourney v7)

• Prethodni članci u seriji: Propozicijske, monadske i poliadske forme. Kvantifikacija i prirodni jezici, Bulovska logika pojmova. Forme, strukture i implikacije, Aristotelova silogistika. Jednostavna i jedina simbolička logika kroz dva milenija, Formalizacije logike sudova. Frege i Kneale, generatori i testovi, Logička korektnost, potpunost i kompaktnost. Gentzenov IF-sustav i Bethova semantička stabla, Zaključivanje u prirodnom i artificijelnom jeziku. Od Aristotela prema Fregeu, Logika sudova. Kondicionali, bikondicionali i implikacije

­

1. ­Struktura i istinitost forme u strukturi

U prethodnom poglavlju bavili smo se, pretežno, sintaksom kvantificiranih formi. Definirali smo kako su one izgrađene od svojih osnovnih elemenata: varijabli, individualnih i predikatskih konstanti, veznika i kvantifikatora. To je prvi korak izgradnje logika predikata (koja je zapravo logika kvantificiranih formi). Sljedeći je korak uvođenje semantike kvantificiranih formi, tj. njihovih interpretacija. Tek u njima kvantificirane forme dobivaju svoje značenje.

Interpretacije kvantificiranih formi bitno su složenije od interpretacija IF-formi pa i od interpretacija bulovskih formi. Interpretacija uvijek ima svoju domenu koju zovemo univerzumom rasprave. On sadrži sve stvari o kojima jezik kvantificiranih formi govori u toj interpretaciji. Univerzum može biti bilo koji skup U, konačan ili beskonačan, jedini uvjet je da nije prazan. Na tom univerzumu interpretiraju se individualne i predikatske konstante. Svakoj individualnoj konstanti pridružuje se neki objekt univerzuma, čije je ona ime. (Pretpostavka je da ime uvijek uspješno imenuje, tj. da uvijek postoji objekt koji ime imenuje. U prirodnim jezicima to nije uvijek tako; usp. Zeus, Hamlet, itd.) Svakoj predikatskoj konstanti pridružuje se skup objekata o kojima je ona istinita. Dakle, jednomjesnoj predikatskoj konstanti pridružuje se skup objekata iz U (tj. podskup od U), dvomjesnoj se pridružuje skup uređenih parova objekata iz U (tj. podskup od U²), tromjesnoj skup uređenih trojki (tj. podskup od U³), itd. Na primjer, jednomjesnom predikatu možemo pridružiti cijeli univerzum U (tj. predikat možemo interpretirati kao istinit o svemu), ili prazan skup ∅ (tj. predikat možemo interpretirati kao istinit ni o čemu)), ili bilo što između te dvije krajnosti. Propozicijske, 0-mjesne, konstante interpretiramo kao u IF–logici, dakle pridružujemo im vrijednosti istinitosti ⊤ ili ⊥.

Semantičku vrijednost koju pridružujemo konstanti γ označit ćemo s |γ| bez obzira radi li se o individualnoj ili predikatskoj konstanti. Ako razmatramo različite interpretacije U i V, onda ćemo semantičke vrijednosti u tim interpretacijama označiti s |γ|_U i |γ|_V. Ako je U univerzum onda s Uⁿ (n > 0) označavamo skup svih uređenih n-torki objekata iz univerzuma U.

DEFINICIJA RELACIJSKE STRUKTURE
(INTERPRETACIJE KVANTIFICIRANIH FORMI)

Relacijska struktura \(\small \mathcal{U}\) sastoji se od univerzuma \(\small U\), koji je neprazni skup, i pridruženja \(\small |\ |\) koje imenskim i predikatskim konstantama pridružuje sljedeće objekte:

(i) za individualnu konstantu \(\small a\): \(\small |a| \in U\),

(ii) za 0-mjesnu predikatsku konstantu \(\small P^{0}\): \(\small |P^{0}| = T \text{ ili } |P^{0}| = \perp\),

(iii) za n-mjesnu predikatsku konstantu \(\small P^{n}\): \(\small |P^{n}| \subseteq U^{n}\).

(Pridruženje \(\small |\ |\) može biti zadano na svim ili samo nekim konstantama, tj. može biti totalno ili parcijalno.) Tako zadana struktura \(\small \mathcal{U}\) označava se:

\(\small \mathcal{U} = (U;|\ |) = (U;\,|a|,\ldots;\,|P^{0}|,\ldots;\,|P^{1}|,\ldots;\,|P^{2}|,\ldots;\,\ldots)\).

(Moderna logika bavi se i općenitijim strukturama, koje osim relacija sadrže i operacije, npr. \(\small +, \cdot, \ldots\). Specijalne strukture koje sadrže samo relacije, a ne i operacije, zovu se relacijskima, dok se one koje sadrže samo operacije, a ne i relacije, zovu operacijskima ili još češće algebarskima.)

Ključni korak u izgradnji logike jest definicija istinitosti forme u strukturi koju možemo shvatiti kao proširenje interpretacije \(\small |\ |\) sa konstanti na forme. To je proširenje definirano sljedećim pravilima koja su intuitivno potpuno jasna, što katkad izaziva zabune. Naime, mnogi očekuju neku kompliciranu ideju skrivenu u formalizmu sljedeće definicije. Jer čemu inače taj formalizam? On je tu da formalno iskaže jednostavnu intuiciju kako bismo je mogli koristiti u formalnim dokazima.

DEFINICIJA ISTINITOSTI ZATVORENE FORME U STRUKTURI

Istinitost zatvorene forme H u strukturi \(\small \mathcal{U} = (U; |\ |)\), u kojoj je interpretacija \(\small |\ |\) definirana na svim konstantama forme H, označava se \(\small \mathcal{U} \models H\) i definira se pravilima:

(i) \(\small \mathcal{U} \models P^0\) akko \(\small |P^0| = \top\),

(ii) \(\small \mathcal{U} \models P^0 a \ldots b\) akko \(\small (|a|, \ldots, |b|) \in |P^n|\),

(iii) \(\small \mathcal{U} \models – F\) akko \(\small  – \mathcal{U} \models F\),

\(\small \mathcal{U} \models F \land G\) akko \(\small \mathcal{U} \models F \land \mathcal{U} \models G\),

\(\small \mathcal{U} \models F \lor G\) akko \(\small \mathcal{U} \models F \lor \mathcal{U} \models G\),

\(\small \mathcal{U} \models F \rightarrow G\) akko \(\small \mathcal{U} \models F \Rightarrow \mathcal{U} \models G\).

(iv) \(\small \mathcal{U} \models \forall x F\) akko \(\small \forall m \in U(\mathcal{U}^a_m \models F(a/x))\),

\(\small \mathcal{U} \models \exists x F\) akko \(\small \exists m \in U(\mathcal{U}^a_m \models F(a/x))\), gdje je a individualna konstanta koja se ne pojavljuje u F.

\(\small \mathcal{U} \models F\) čitamo „forma F je istinita u strukturi U“ ili „struktura U ispunjava formu F“.

Pravila (i) – (iii) ne treba dodatno objašnjavati. Pravilo (iv) kaže da je zatvorena forma \(\small \forall x F(x)\) istinita ako je zatvorena forma \(\small F(a/x)\), koja se dobiva substitucijom individualne konstante \(\small a\) na sva mjesta varijable \(\small x\), istinita za sve moguće interpretacije konstante \(\small a\). To preciznije formuliramo na sljedeći način. Za interpretaciju \(\small U^{a}_{m}\) kažemo da je \(\small (a/m)\)-varijanta od \(\small U\) ako se ona od \(\small U\) razlikuje samo po tome što \(\small a\) interpretira kao \(\small m\). Dakle, zatvorena forma \(\small \forall x F(x)\) istinita je u strukturi \(\small U\) ako je zatvorena forma \(\small F(a/x)\) istinita u svakoj njenoj varijanti \(\small U^{a}_{m}\), a zatvorena forma \(\small \exists x F(x)\) je istinita u \(\small U\) ako je zatvorena forma \(\small F(a/x)\) istinita u nekoj njenoj varijanti \(\small U^{a}_{m}\). Sve to pod uvjetom da se \(\small a\) ne pojavljuje u \(\small F(a/x)\), jer želimo da sve konstante u \(\small \forall x F(x)\) i \(\small \exists x F(x)\) zadrže svoju izvornu interpretaciju iz \(\small U\). I to je pravilo (iv).

Pravila (i) – (iv) na jednoznačan način pridružuju vrijednosti istinitosti, \(\small \top \) ili \(\small \bot\), svakoj zatvorenoj formi čije su individualne i predikatske konstante već interpretirane sa \(\small |\ |\).

Ključni logički pojmovi (implikacija, konzistentnost, valjanost, ekvivalencija) i dalje su specijalni su slučajevi generalizirane implikacije.

DEFINICIJA GENERALIZIRANE IMPLIKACIJE

Skup zatvorenih formi Γ(generalizirano) implicira skup zatvorenih formi Δ, oznakom Γ⊨Δ, akko ne postoji struktura u kojoj su sve forme iz Γ istinite i sve forme iz Δ neistinite. Drugim riječima, svaka struktura koja sve premise iz Γ čini istinitima, čini istinitom bar jednu konkluziju iz Δ.

Skup formi Γ je konzistentan, oznakom ⟐Γ, akko Γ ⊭ (tj. Γ ⊭ ∅). Drugim riječima, postoji struktura u kojoj su sve forme iz Γ istinite.

Forma A je valjana, oznakom ⊡ A, akko ⊨ A (tj. ∅ ⊨ A). Drugim riječima, forma A je istinita u svim strukturama.

Forme A i B međusobno su ekvivalentne, oznakom A ⇔ B, akko A ⊨ B i B ⊨ A. Drugim riječima, forme A i B istinite su u istim strukturama.

(Primijetimo da se znak ⊨ u logici koristi dvojako. Za generaliziranu implikaciju i za istinitost u strukturi. To neće dovesti do zabune jer se u prvom slučaju s obje strane od ⊨ nalaze forme, dok je u drugom zapisu lijevo uvijek struktura, a samo desno su forme.)

Relacija ⊨ u logici kvantificiranih formi i dalje zadovoljava strukturna i IF–pravila iz trećeg poglavlja, ali u njoj vrijede i pravila kvantifikacije.

PRAVILA KVANTIFIKACIJE

­­

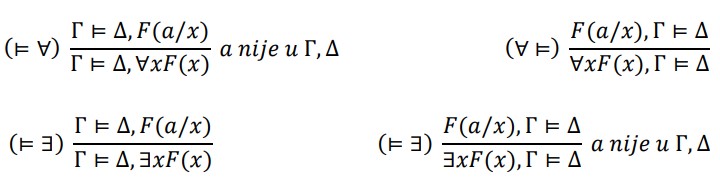
Da vrijede (∀⊨) i (⊨∃) slijedi iz ∀ x F(x) ⊨ F(a/x) i F(a/x) ⊨ ∃xF(x). Dokaz pravila (⊨ ∀) i (⊨ ∃) malo je složeniji. Pretpostavimo da Γ ⊭ Δ,∀xF(x), te da se a ne pojavljuje u Γ i Δ. Onda postoji struktura \(\small \mathcal{U}\) u kojoj su sve forme iz Γ istinite, sve iz Δ neistinite i u kojoj je ∀xF(x) neistina. Iz \(\small \mathcal{U}\) ⊭ ∀xF(x) slijedi da u univerzumu U postoji m takav da \(\small \mathcal{U}^{a}_{m}\) ⊭ F(a/x). No to znači da \(\small \mathcal{U}^{a}_{m}\) dokazuje Γ ⊭ Δ, F(a/x). Dakle, iz Γ ⊭ Δ, ∀xF(x) slijedi Γ ⊭ Δ, F(a/x). To znači da iz Γ ⊨ Δ, F(x), slijedi Γ ⊨ Δ, ∀xF(x). Time smo dokazali (∀⊨). Na isti se način dokazuje (⊨∃).

Ta pravila možemo razumjeti i kao pravila dokazivanja:

(∀ ⊨) Ako nešto slijedi iz F(a/x) onda to slijedi i iz ∀xF(x);

(⊨∃) Ako iz nečega slijedi F(a/x) onda iz toga slijedi i ∃xF(x);

(⊨∀) Ako F(a) slijedi iz nečega neovisno o tome što je a, onda iz toga slijedi i ∀xF(x);

(∃ ⊨) Ako iz F(a) slijedi nešto neovisno o tome što je a, onda to slijedi i iz ∃xF(x).

Ta pravila, uz strukturna i IF–pravila, čine Gentzenov sekventni sustav za logiku kvantificiranih formi (tzv. Gentzenov sekventni Q-sustav) koji je očito korektan, a dokazat ćemo i da je potpun.

2. Bethove semantička stabala za kvantificirane forme

Potpunost Gentzenovog IF-sustava slijedila je iz Bethove metode semantičkih stabala za IF-forme. Potpunost Gentzenovog Q-sustava slijedit će iz Bethove metode semantičkih stabala za kvantificirane forme. Prije nego metodu detaljno opišemo evo par primjera.

Da ∃xFx ∧ ∃xGx ⊭ ∃x(Fx ∧ Gx) dokazujemo tako da izgradimo strukturu koja formu ∃xFx ∧ ∃xGx vrednuje s ⊤, a formu ∃x(Fx ∧ Gx) vrednuje s ⊥:

­­

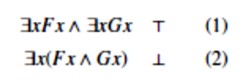
Prvi zahtjev ostvaruje se tako da ∃xFx i ∃xGx budu ⊤:

­­

Zahtjevi ∃xFx⊤ i ∃xGx⊤ ostvaruju se tako da u univerzum uvedemo objekte a i b takve da Fa i Gb budu ⊤.

­ ­

Kada ispunjavamo zahtjeve oblika ∀xA(x)⊤ i ∃xA(x)⊥ moramo brinuti o svemu što je u univerzumu. Naime, ti će zahtjevi biti ispunjeni tek kada se ispune zahtjevi A(a)⊤, A(b)⊤,…; odnosno A(a)⊥, A(b)⊥,…; za sve objekte a,b,… koji su u univerzumu. Zato uz zahtjeve oblika ∀xA(x)⊤ i ∃xA(x)⊥ ispisujemo sve objekte uvedene u univerzum (vidi red (2) u stablu). Ti zahtjevi se ispunjavaju o svakom pojedinom objektu, što označavamo zaokruživanjem svakog pojedinog objekta:

­­

Zahtjev Fa∧Ga⊥ može se ostvariti na dva načina, tako da Fa bude ⊥ ili da Ga bude ⊥. Te dvije alternative postaju dvije grane našeg semantičkog stabla. Zahtjev Fb∧Gb⊥ također se ostvaruje na dva alternativna načina, Fb⊥ ili Gb⊥, što otvara po dvije nove grane na svakoj od prethodne dvije:

­­

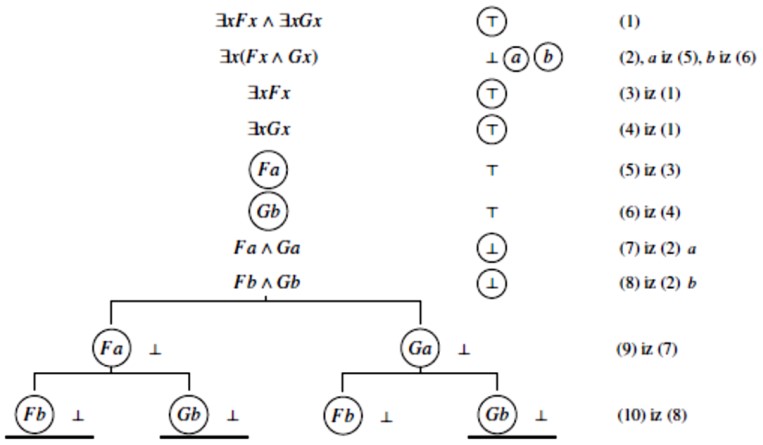
Stablo je potpuno razvijeno, jer više nema zahtjeva koje bi trebalo ispuniti (svi su zahtjevi zaokruženi). Prva, druga i četvrta grana sadrže kontradiktorne zahtjeve Fa ⊤⊥, i Gb ⊤⊥, pa su zato zatvorene. S treće grane možemo očitati interpretaciju (strukturu) koji zadovoljava početne zahtjeve i dokazuje ∃xFx∧∃xGx⊭∃x(Fx∧Gx). Njen je univerzumu {a,b}. Atomarni zahtjevi su |Fa|=⊤,|Gb|=⊥,|Gb|=⊥i |Fb|=⊥ Možemo je opisati i tablicom:

­­

Drugi primjer je dokaz valjanosti „argumenta crtača“ (za koji znamo da nije ni IF ni monadski valjan):

­­

Njegova je poliadska forma

­­

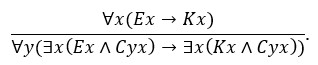
Njegovo semantičko stablo izgleda ovako:

­­

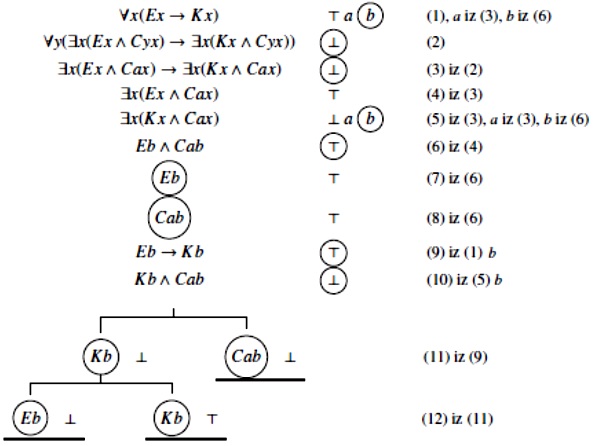
Sve su se grane zatvorile, što znači da ne postoji interpretacija koji bi oborila našu poliadsku implikaciju, tj. ∀x(Ex → Kx) ⊨ ∀y (∃x(Ex ∧ Cyx) → ∃x(Kx ∧ Cyx)).

U protekla dva primjera dokazali smo intuitivno očiglednu neimplikaciju i intuitivno očiglednu implikaciju. Što bismo rekli o sljedećoj implikaciji

\(\small \forall x (Gx \rightarrow Hx),\ \exists x (Fx \land Hx)\) ⊨ \(\small \forall x (Fx \rightarrow \overline{G}x)\)?

Vrijedi li ona ili ne vrijedi? Odgovor možda nije očigledan, ali ga lako nalazimo metodom semantičkih stabala:

­­

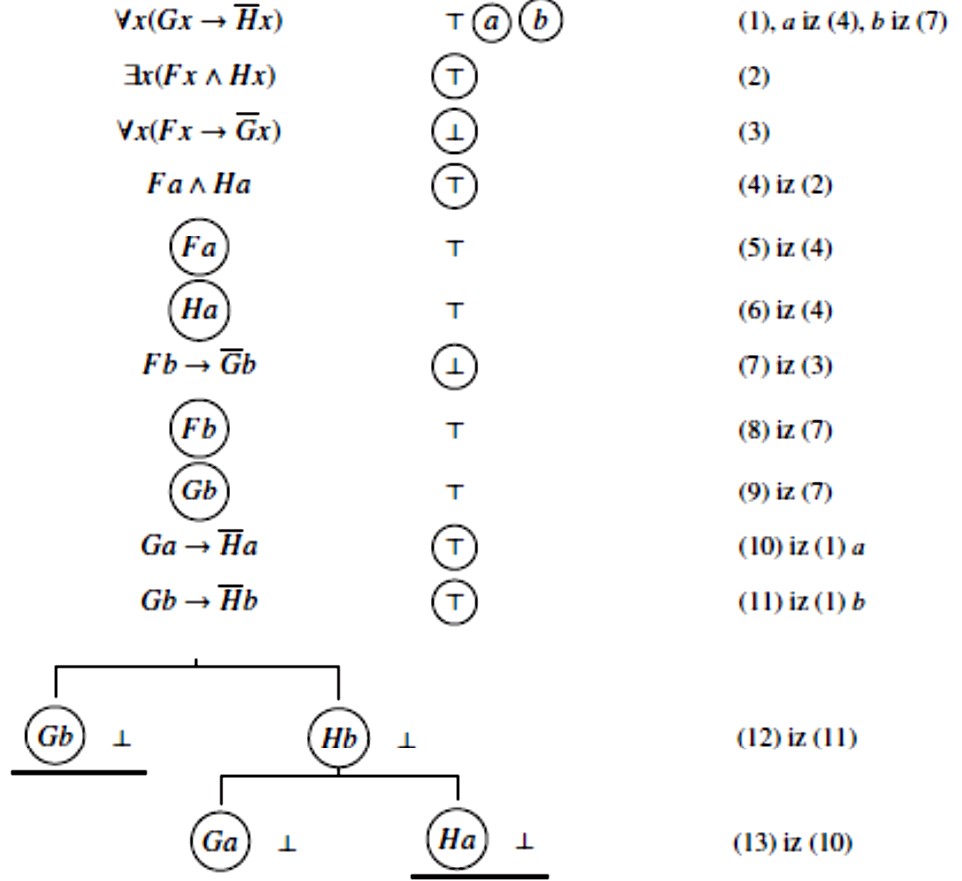
Srednja grana se nije zatvorila i s nje možemo očitati model koji dokazuje da \(\small \forall x (Gx \rightarrow Hx),\ \exists x (Fx \land Hx)\) ⊨ \(\small \forall x (Fx \rightarrow \overline{G}x)\).

­­

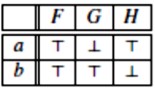
Ovi primjeri jasno pokazuju da metoda semantičkih stabala za kvantificirane forme proširuje IF–metodu, time što joj dodaje četiri nova semantička pravila za kvantificirane forme.

­­

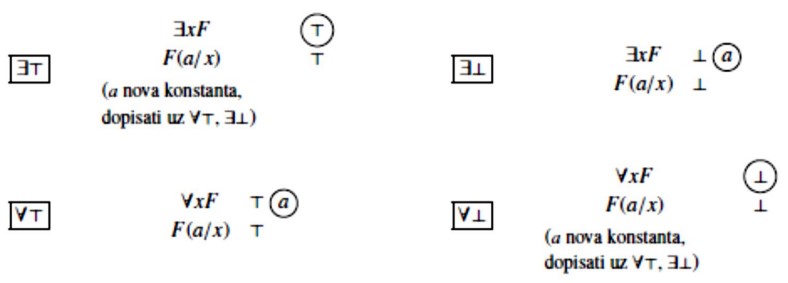
Primjenom pravila (∃⊤) na formu ∃xF uvodimo novi a∈U koji „svjedoči“ da je ∃xF ⊤ (jer je F(a/x)⊤) i taj je zahtjev do kraja analiziran. To naznačujemo zaokruženim ⊤.

Primjenom pravila (∀⊥) na formu ∀xF uvodimo novi a∈U koji „svjedoči“ da je ∀xF⊥ (jer je F(a/x)⊥) i taj je zahtjev do kraja analiziran. To naznačujemo zaokruženim ⊥.

Da do kraja analiziramo zahtjev ∀xF ⊤ moramo F „potvrditi“ o svakom objektu a∈U. Svaka parcijalna potvrda objektom a naznačena je zaokruženim a.

Da do kraja analiziramo zahtjev ∃xF ⊥ moramo F „opovrći“ o svakom objektu a∈U. Svako parcijalno opovrgavanje objektom a naznačena je zaokruženim a.

3. Potpunost i korektnost logike predikata

Da do kraja analiziramo zahtjev ∃xF⊥ moramo F „opovrći“ o svakom objektu a ∈ U. Svako parcijalno opovrgavanje objektom a naznačeno je zaokruženim a.
Uvedenih objekata a, b, … može biti beskonačno mnogo ako ih stalno iznova generiraju zahtjevi oblika ∃xF ⊤ i ∀xF⊥. To znači da semantička stabla za kvantificirane forme mogu biti i beskonačna. Na primjer, ispitajmo metodom semantičkih stabala vrijedi li implikacija ∀x∃yDxy ⊨ ∃y∀xDxy.

­­

Stablo (koje u ovom slučaju čini jedna grana) nikada se neće završiti pa ni zatvoriti, jer svaki objekt o zahtjeva dva nova objekta o₁ i o₂ takva da je Doo₁ ⊤ i Doo₂ ⊥. S te beskonačne otvorene grane možemo očitati sljedeću beskonačnu strukturu koja dokazuje ∀x∃yDxy ⊭ ∃y∀xDxy:

­­

Strelica između o i o₁ znači da je Doo₁ ⊤, a crtice između o i o₂ znače da je Doo₂ ⊥.

(Monadske forme nemaju taj problem, jer njihov preneksni oblik može imati proizvoljan redoslijed kvantifikatora, što smo dokazali u prethodnom poglavlju. Zato ih uvijek možemo zamijeniti ekvivalentnim zahtjevima oblika ∃ …∃∀ …∀F ⊤ i ∀ …∀∃ …∃F ⊥, u kojima F nema kvantifikatora. Takvi zahtjevi očito u univerzum uvode samo konačno mnogo objekata pa je njihovo semantičko stablo konačno.)

S pravom se možete pitati zašto smo konstruirali tako složenu strukturu za obaranje implikacije ∀x∃yDxy ⊨ ∃y∀xDxy. Do jednostavnije strukture dolazimo ako se malo držimo pa malo ne držimo pravila o novoj konstanti pri primjeni pravila ∃⊤ i ∀⊥:

­­

Grana je potpuno razvijena i otvorena pa s nje lako očitavamo interpretaciju koja dokazuje da ∀x∃yDxy ⊭ ∃y∀xDxy.

­­

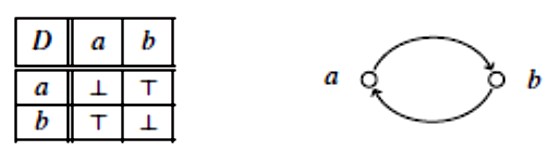
No, uvođenjem starih konstanti pri primjeni ∃⊤ i ∀⊥ mogli bismo doći i do pogrešnog zaključka:

­­

Stablo se zatvorilo. Znači li to da ∀x∃yDxy ⊨ ∃y∀xDxy? Ne, ono se zatvorilo jer nismo uvodili nove objekte u (5) i (6). Time smo univerzum sveli na samo jedan objekt a, pa je ono što možemo zaključiti samo to da “implikacija” vrijedi u strukturama s jednočlanim univerzumom. Naravno, to nije implikacija.

Sve što smo ilustrirali ovim primjerima vrijedi i općenito:

(1) Ako, s ograničenjem na nove objekte (koje je dio pravila ∃⊤ i ∀⊥) izgeneriramo zatvoreno stablo, početni poliadski zahtjevi ne mogu se ispuniti.

(2) Ako, s ili bez ograničenja na nove objekte, izgeneriramo (konačnu ili beskonačnu) otvorenu i potpuno razvijenu granu, onda atomarni zahtjevi s te grane definiraju interpretaciju koja ispunjava početne poliadske zahtjeve.

Znači li to da je metoda semantičkih stabala metoda odluke za poliadsku logiku? Ne znači. Kao prvo, nismo dokazali da primjena te metode nužno vodi do (1) ili (2). Naime, IF–zahtjevi se opetovanom primjenom IF–pravila uvijek svode na konačno mnogo atomarnih zahtjeva. To osigurava da metoda u IF–slučaju uvijek završava stablom koje je (1) zatvoreno, ili je (2) potpuno razvijeno i otvoreno (usp. treće poglavlje). S druge strane, vidjeli smo da se kvantificirani zahtjevi (stalnim uvođenjem novih konstanti) mogu multiplicirati u beskonačno mnogo novih zahtjeva. To znači da se stablo s poliadskim zahtjevima može razviti i tako da se na neke zahtjeve njihova pravila nikada ne primjenjuju (npr. zato jer se stalno bavimo novim zahtjevima tipa ∀ ∃⊤a₀ a₁ a₂ …). Drugim riječima, razvijanje stabla s poliadskim zahtjevima nužno ne osigurava (1) zatvaranje stabla ili (2) izgradnju njegove otvorene i potpuno razvijene grane, kao u slučaju IF–zahtjeva.

Zato stablo treba razvijati tako da se svaki zahtjev prije ili kasnije analizira (tj. da se na svaki zahtjev prije ili kasnije primijeni njegovo pravilo). To osigurava sljedeća ciklička metoda semantičkih stabala.

DEFINICIJA CIKLIČKE METODE SEMANTIČKIH STABALA

Konačnu poliadsku ne-implikaciju Γ ⊭ Δ testiramo tako da polazeći od zahtjeva Γ ⊤ i Δ ⊥ semantičko stablo gradimo u ciklusima od tri koraka:

(i) najprije primijenimo sva IF–pravila koja je moguće primijeniti,

(ii) zatim primijenimo sva ∃⊤ i ∀⊥ pravila koja je moguće primijeniti,

(iii) i na kraju primijenimo sva ∃⊥ i ∀⊤ pravila koja je moguće primijeniti.

Dokle god ima neispunjenih zahtjeva cikluse ponavljamo opisanim redoslijedom.

Ciklička metoda osigurava da svaki zahtjev prije ili kasnije bude analiziran. Ono što naša metoda u poliadskom slučaju ne osigurava jest da će izgradnja stabla uvijek završiti u konačno mnogo koraka. No bez obzira na to, za konačni Γ ⊭ Δ, ciklička izgradnja stabla ili (1) završava zatvaranjem stabla ili (2) generira bar jednu (konačnu ili beskonačnu) otvorenu i potpuno razvijenu granu. U slučaju (1) Γ ⊨ Δ, u slučaju (2) Γ ⊭ Δ.
Ipak, ni ciklička metoda nije metoda odluke za poliadsku logiku. Ako implikacija vrijedi metoda će to dokazati u konačno mnogo koraka (izgradnjom zatvorenog stabla). Ako implikacija ne vrijedi, izgradnja stabla može se nastaviti u beskonačnost. Problem je u tome da nemamo kriterij kojim bismo odlučili o kojem je slučaju riječ. Ako se stablo još nije zatvorilo mi ne znamo odlučiti je li to zato što nismo napravili dovoljan broj koraka ili zato što se nikada ni neće zatvoriti. Drugim riječima, metoda semantičkih stabala je pozitivni test za poliadske implikacije Γ ⊨ Δ, ali nije negativni test.

TEOREM O POSTOJANJU POZITIVNOG TESTA ZA Γ⊨Δ

Metoda semantičkih stabala je pozitivni test za poliadske implikacije, tj. ako Γ ⊨ Δ vrijedi onda će metoda to dokazati u konačno mnogo koraka (zatvaranjem semantičkog stabla). Metoda nije negativni test za poliadske implikacije, tj. ako Γ ⊭ Δ metoda to nužno ne dokazuje u konačno mnogo koraka.

(Prisjetimo se da za neko svojstvo imamo postupak odluke akko za to svojstvo imamo i pozitivni i negativni test. Naime, postupak odluke za neko svojstvo je onaj postupak koji u svakom pojedinom slučaju u konačno mnogo koraka dokazuje vrijedi li to svojstvo ili ne. Dakle, postupak odluke očito je i pozitivan i negativan test. S druge strane, ako na slučaj koji ispitujemo paralelno primijenimo i pozitivni i negativni test jedan će u konačno mnogo koraka dovesti do odluke. To znači da je paralelna primjena pozitivnog i negativnog testa zapravo postupak odluke.)

Sada je lako dokazati da je Gentzenov sekventni Q-sustav potpun. Kao i u IF–slučaju (v. treće poglavlje) „staro“ zatvoreno semantičko stablo za Γ ⊭ Δ zapravo je „novi“ dokaz od Γ ⊨ Δ u sekventnom sustavu (kada ga gledamo u obrnutom smjeru). Evo primjera kojim pokazujemo kako zatvoreno stablo za ∃y∀xFxy ⊭ ∀x∃yFxy prevodimo u Gentzenov Q-dokaz od ∃y∀xFxy ⊨ ∀x∃yFxy:

­­

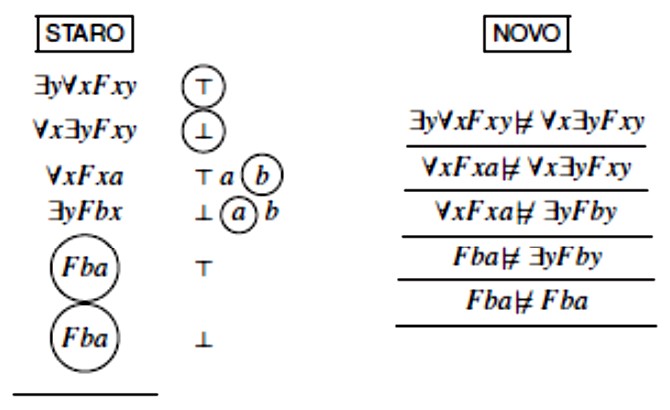
U obje notacije semantičko stablo se zatvorilo, što znači da ∃y∀xFxy ⊨∀x∃yFxy. Obrnemo li stablo u novoj notaciji i zamijenimo li svaki⊭ s ⊨ , dolazimo do dokaza od ∃y∀xFxy ⊨ ∀x∃yFxy u Gentzenovom sekventnom Q–sustavu:

­­

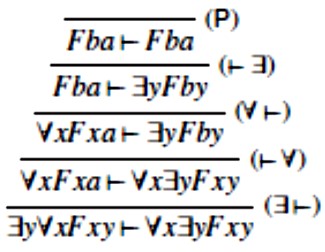
Opet smo dokazali i nešto više, kao i u trećem poglavlju. U zatvorenim semantičkim stablima “čitanim naopako” nikada se ne pojavljuju ni rez ni slabljenje. To znači da je potpun već i Gentzenov Q–sustav bez reza i slabljenja. Obično se kaže da su rez i slabljenje eliminabilni iz Gentzenovog Q–sustava.

Može se dokazati da je Gentzenov Q–sustav ekvivalentan Fregeovom, Gentzenovom prirodnom i Knealeovom sustavu, kada ih proširimo odgovarajućim aksiomima i pravilima kvantifikacije:

Fregeov sustav (* znači da x nije u A)

­­

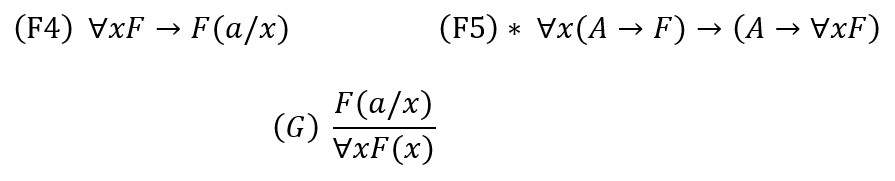
Gentzenov sustav (* znači da a nije ni u pretpostavkama ni u C)

­­

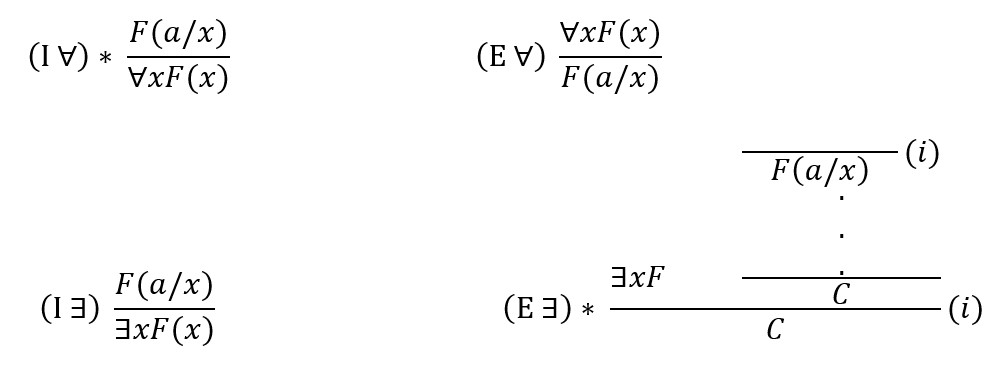
Knealeov sustav (* znači da a nije ni u pretpostavkama ni u konkluzijama)

­­

Dakle, sve su to korektni i potpuni sustavi dokazivanja valjanih formi i implikacija logike predikata.