Logika sudova. Kondicionali, bikondicionali i implikacije

U drugom nastavku serijala o logici, Zvonimir Šikić proširuje teorijske temelje logike sudova funkcijama kondicionalom i bikondicionalom, te pojašnjava logički pojam implikacije unutar IF-sekventi.

• Naslovna fotografija: Njemački filozof, matematičar i logičar Gottlob Frege.

• Prethodni članak u seriji: Zaključivanje u prirodnom i artificijelnom jeziku. Od Aristotela prema Fregeu

1. Kondicional i bikondicional

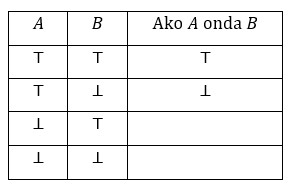
Osim binarnih veznika “i” i “ili” u prirodnim jezicima često se koristi binarni veznik “ako onda”. Tvrdnju oblika “ako  onda ” zovemo kondicionalom. Njezinu A komponentu zovemo antecendentom, a njenu B komponentu konzekventom. P̅Q̅R

Kondicional najčešće nije istinosna funkcija. Pod kojim bismo uvjetima kondicional držali istinitim? Čak je i postavljanje tog pitanja neobično, jer afirmaciju tvrdnje “ako onda ” manje doživljavamo kao afirmaciju kondicionala, a više kao uvjetnu afirmaciju konzekvente. Ako se pokaže da je antecedenta istinita onda stojimo iza konzekvente i priznat ćemo našu grešku ako se ona pokaže neistinitom. Ako se pak pokaže da je antecedenta neistinita naša afirmacija kondicionala postaje praznom, kao da nije ni učinjena. Mogli bismo reći da tako shvaćeni kondicional ima djelomičnu tablicu istinitosti:

­­

U IF–logici odustajemo od takvog razumijevanja kondicionala i držimo ga istinosno funkcionalnim veznikom (čija je tablica potpuna). Ako je antecedenta istinita onda vrijednost istinosti kondicionala poistovjećujemo s vrijednošću istinosti njegove konzekvente, kao u prirodnim jezicima. Ako je antecedenta neistinita onda kondicional smatramo istinitim bez obzira na vrijednost istinitosti njegove konzekvente, suprotno praksi prirodnih jezika. Tako upotpunjeni kondicional, oznakom →, često se zove materijalnom implikacijom (što nije dobro, jer je implikacija pojam bitno različit od kondicionala).

DEFINICIJA KONDICIONALA

­­

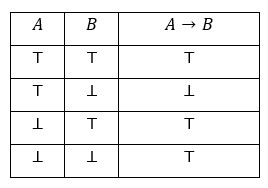
Očito vrijede ekvivalencije: \( \small A \rightarrow B \Leftrightarrow \neg (A \land \overline{B}) \quad A \rightarrow B \Leftrightarrow \overline{A} \vee B \)

U skladu s tom IF–definicijom sljedeće su tvrdnje istinite:

(1) Ako je Zagreb u Hrvatskoj onda je more slano.

(2) Ako je Zagreb u Sloveniji onda je more slano.

(3) Ako je Zagreb u Sloveniji onda je more slatko.

To sigurno izgleda neobično, ali jednako bi neobično izgledalo da neku od tvrdnji (1), (2) ili (3) proglasimo neistinitom. Neobične su nam tvrdnje (1), (2) i (3), a ne to jesu li one istinite ili neistinite. Naprosto nije uobičajeno praviti kondicionale od jednostavnijih komponenti čije su istinosne vrijednosti poznate. Razlog za to je očit: čemu tvrditi nešto poput (1) i (2) ako smo u poziciji da iskažemo informativniju i kraću tvrdnju: “More je slano”? Zašto tvrditi (3) ako možemo reći kraće i informativnije “Zagreb nije u Sloveniji”? Uostalom, isto vrijedi i za veznik “ili”.

(4) Zagreb je u Hrvatskoj ili je more slatko.

Tvrdnja (4) zvuči jednako neobično kao i tvrdnje (1)–(3), i to iz istih razloga. Informativnije je i jednostavnije reći “Zagreb je u Hrvatskoj” nego tvrditi (4).

Tko tvrdi “Ako A onda B” (odnosno “A ili B“) obično nije siguran u pojedinačnu istinitost ili neistinitost tvrdnji A i B, nego ima neke razloge da ne vjeruje u kombinaciju “A i nije B” (odnosno, “Nije A i nije B“). Dakle, onaj koji tvrdi:

Ako Ana ima upalu slijepog crijeva onda hitno treba ići u bolnicu.

tvrdi to zato što zna koje su moguće komplikacije upale slijepog crijeva, a ne zato što zna ima li Ana upalu i treba li ići u bolnicu.

Sve što smo rekli o kondicionalu “ako onda” vrijedi i za bikondicional “ako i samo ako”, koji skraćeno zapisujemo “akko”. Naime, bikondicional “A akko B” je konjunkcija kondicionala “Ako A onda B” i “Ako B onda A“. Njegova IF–varijanta označava se s ↔ i često se naziva materijalnom ekvivalencijom (što nije dobro, jer je ekvivalencija pojam bitno različit od bikondicionala).

DEFINICIJA BIKONDICIONALA

­­

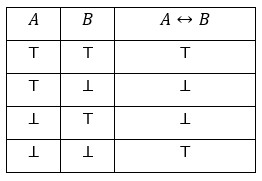
Očito vrijede ekvivalencije: \( \small A \leftrightarrow B \Leftrightarrow (A \land B) \vee (\overline{A} \land \overline{B}) \quad A \leftrightarrow B \Leftrightarrow (A \rightarrow B) \land (B \rightarrow A) \)

U prirodnim jezicima idiomi “ako onda” i “ako i samo ako” također se koriste za izražavanje implikacije i ekvivalencije. U matematici je ta uporaba čak dominantna. To, nažalost, dovodi do brkanja kondicionala s implikacijom i bikondicionala s ekvivalencijom. Njihov stvarni odnos je sljedeći: A implicira B, tj. A ⇒ B, ako ne postoji interpretacija u kojoj je A istinito i B neistinito, što znači da ne postoji interpretacija u kojoj je A → B neistinito. Dakle, implikacija A ⇒ B izriče valjanost (logičku istinitost) kondicionala A → B. Slično, ekvivalencija A ⇔ B izriče valjanost (logičku istinitost) bikondicionala A ↔ B. To je izuzetno važna veza, ali nije identitet (jer istinitost nije isto što i logička istinitost).

Dakle, kondicional i bikondicional omogućuju nam da implikaciju i ekvivalenciju svedemo na valjanost (logičku istinitost), kao što nam je negacija omogućila da valjanost i implikaciju svedemo na konzistentnost (usp. prvi nastavak).

TEOREM O VEZI KONDICIONALA, IMPLIKACIJE I VALJANOSTI

Forma A implicira formu B akko je kondicional A → B valjan.

Zapisano simbolima: A ⇒ B akko ⊡ (A → B).

TEOREM O VEZI BIKONDICIONALA, EKVIVALENCIJE I VALJANOSTI

Forma A ekvivalentna je formi B akko je bikondicional A ↔ B valjan.

Zapisano simbolima: A ⇔ B akko ⊡ (A ↔ B).

Očito je da su istinosne funkcije → i ↔ (kako smo ih ranije definirali) jedine istinosne funkcije koje na ovaj način implikaciju i ekvivalenciju svode na valjanost. To je još jedan razlog (možda i najvažniji) da IF–funkcije → i ↔ definiramo onako kako smo ih definirali.

Osnovni fond IF–veznika kojima ćemo se ubuduće koristiti čine konjunkcija ∧, alternacija ∨, negacija −, kondicional → i katkada bikondicional ↔. Dakle, naše IF–forme bit će {∧,∨,−,→} forme, koje definiramo kao i prije. Uz nove veznike → i ↔ uvodimo i novu konvenciju da oni razdvajaju jače od starih veznika ∧, ∨ i −. Dakle, P ∨ Q → R je pokrata za ((P ∨ Q) → R) dok je −P ↔ Q pokrata za ((−P) ↔ Q).

Forme su razumljivije kada koristimo sve te veznike, iako otprije znamo da su dovoljni {∧,−} ili {∨,−}. Lako se vidi da su dovoljni i {−,→}, njih je npr. koristio Frege.. Naime, iz \( \small \overline{A} \vee B \Leftrightarrow A \rightarrow B \) i \( \small \neg (A \land \overline{B}) \Leftrightarrow A \rightarrow B \) lako slijedi:

\(\small A \vee B \Leftrightarrow \overline{\overline{A}} \vee B \Leftrightarrow \overline{A} \rightarrow B \) i \(\small A \land B \Leftrightarrow \neg \neg (A \land \overline{\overline{B}}) \Leftrightarrow \neg (A \rightarrow \overline{B}) \).

To znači da se alternacija i konjunkcija mogu se izraziti pomoću kondicionala i negacije. Primijetimo još da je \( \small \overline{A} \Leftrightarrow A \rightarrow \bot \) što nas dovodi do {→, ⊥}, kao još jednog zanimljivog generatora svih IF–veznika.

2. IF–logika i algebra skupova

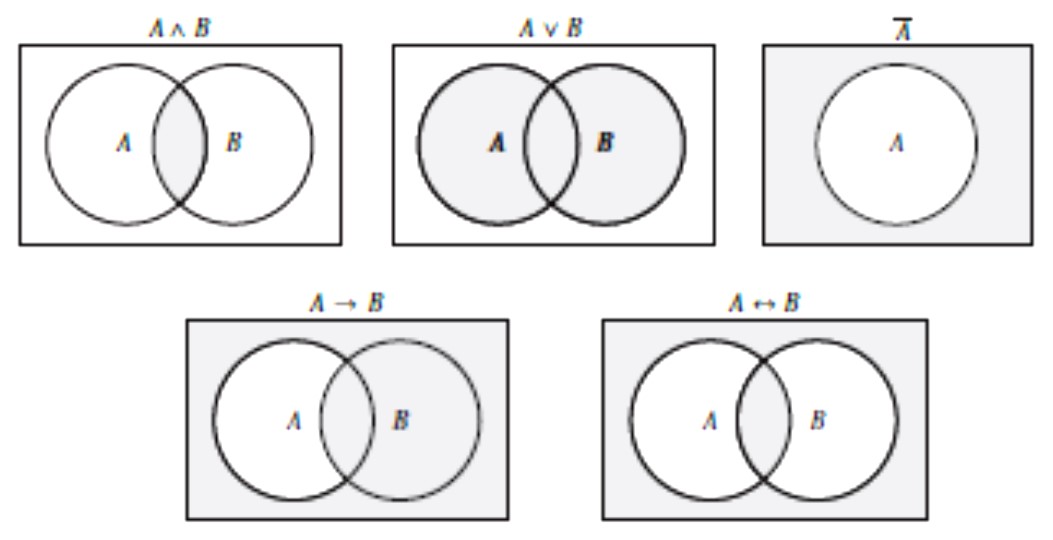
Svakoj IF–formi možemo pridružiti skup svih totalnih interpretacija u kojima je ona istinita. Taj skup predstavlja tu formu i često ga identificiramo s tom formom. (Budući da su međusobno ekvivalentne forme predstavljene identičnim skupovima, time identificiramo i međusobno ekvivalentne forme. ) Ako su forme A i B identificirane sa skupovima totalnih interpretacija u kojima su one istinite, onda A ∧ B i A ∨ B identificiramo s presjekom i unijom tih skupova, a \( \small \overline{A}\) s komplementom od A. (Naime, skup interpretacija u kojima je forma \( \small \overline{A}\) istinita je komplement skupa interpretacija u kojima je forma A istinita; skup interpretacija u kojima je forma A ∧ B istinita je presjek skupova interpretacija u kojima su istinite forme A i B  itd.) Kondicional A → B i bikondicional A ↔ B ekvivalentni su s \( \small \overline{A} \vee B\) i \( \small AB \vee \overline{AB}\), pa i njih identificiramo s odgovarajućim skupovima. To prikazujemo sljedećim skupovnim dijagramima, koji se zovu Eulerovim dijagramima.

­­

Primijetimo (vidi donje dijagrame) da dijagram koji prikazuje 1 atomarnu formu P sadrži 2¹ područja (tzv. ćelije): \( \small P \) i \( \small \overline{P}\). Dijagram koji prikazuje 2 atomarne forme \( \small P \) i \( \small Q\) sadrži 2² = 4 ćelije: \( \small PQ, P\overline{Q},\overline{P}Q,\overline{PQ} \). Dijagram koji prikazuje 3 atomarne forme  sadrži 2³ = 8 ćelija: \( \small PQR, PQ\overline{R},P\overline{Q}R,\overline{P}QR,P\overline{QR},\overline{P}Q\overline{R}, \overline{PQ}R, \, i \, \overline{PQR}\). I tako dalje.

­­

­­

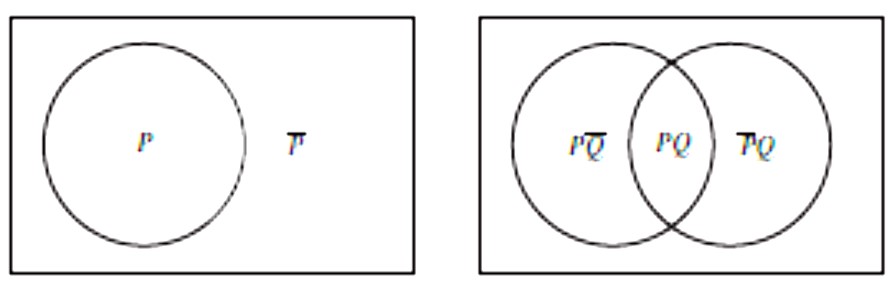
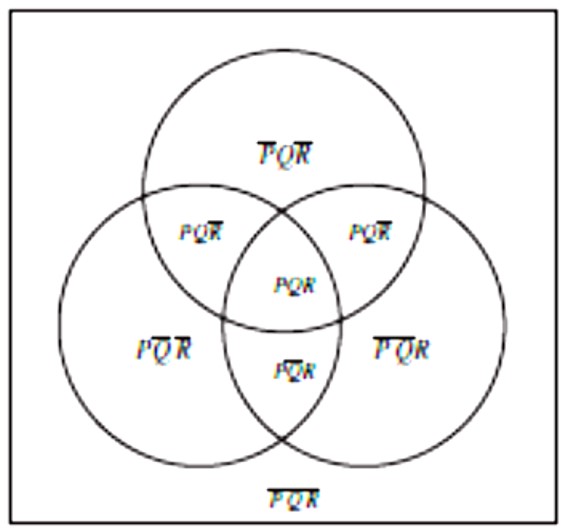
Svaka ćelija odgovara jednoj parcijalnoj interpretaciji prikazanih formi. Na primjer, ćelija \( \small \overline{P}\overline{Q}R\) sadrži totalne interpretacije u kojima je P = ⊥, Q = ⊥ i R = ⊤,  tj. predstavlja parcijalnu intepretaciju (P, Q, R) = (⊥,⊥,⊤). Svih 8 ćelija predstavlja svih 8 parcijalnih interpretacija formi P, Q i R. Dakle, ono što je 8 redaka u tablici istinitosti za atome P, Q i R, to je 8 ćelija u skupovnom prikazu.

Nadalje, svaka istinosna funkcija F (P, Q, R) pridružuje istinosnu vrijednosti ⊤ ili ⊥ svakoj pojedinoj interpretaciji od P, Q i R. Dakle, njezin skupovni prikaz čine točno one interpretacije u kojima je F (P, Q, R) istinita. To znači da je F (P, Q, R) prikazana unijom ćelija u kojima vrijedi F (P, Q, R) = ⊤. Na primjer, istinosna funkcija F (P, Q, R) zadana sljedećom tablicom ima sljedeći skupovni prikaz.

­­

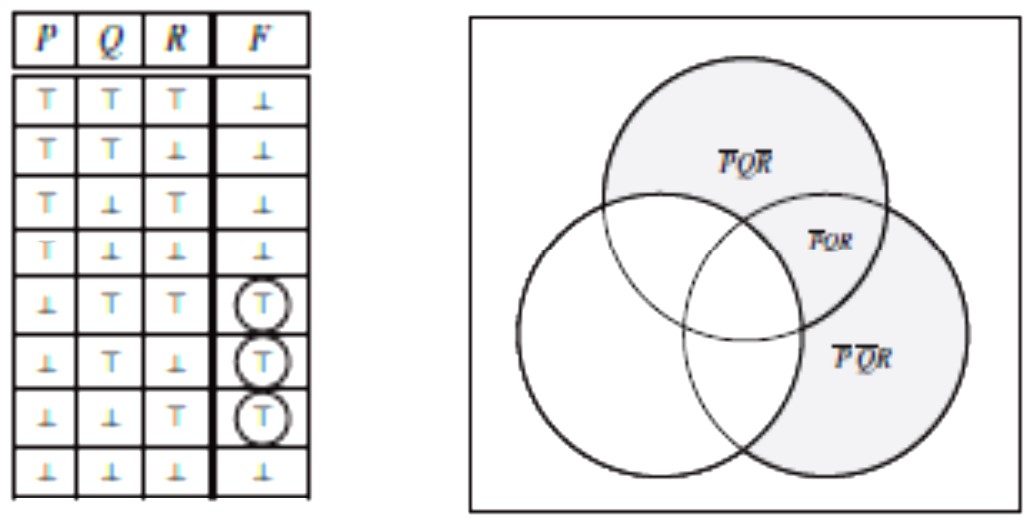
Iz oba prikaza, tabličnog i skupovnog, možemo očitati da je

\(\small F \Leftrightarrow \overline{P}Q R \vee \overline{P}Q\overline{R} \vee \overline{P}\overline{Q}R\)

Drugim riječima, iz oba prikaza lako očitavamo potpunu alternacijsku normalnu formu od F (u skupovnom dijagramu ona je doslovno “vidljiva”.)

Osim što omogućuju da vrlo zorno prikazujemo IF–forme, skupovni dijagrami, uz Vennove konvencije, omogućavaju zorno prikazivanje logičkih svojstava formi (npr. valjanosti i konzistentnosti) i logičkih odnosa među formama (npr. implikacije i ekvivalencije).

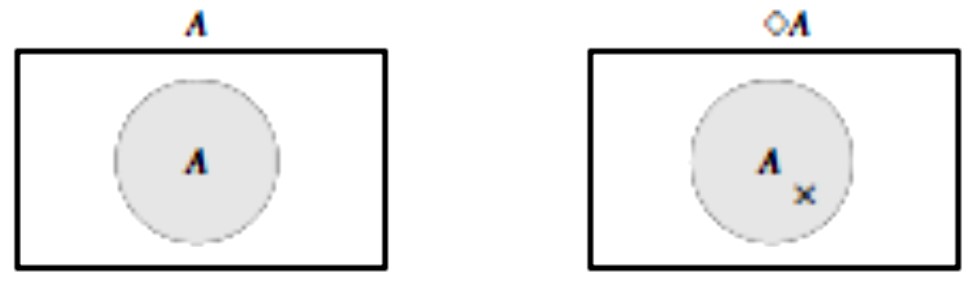
Na primjer, što znači da je forma A valjana? To znači da nema interpretacije u kojoj je ona neistinita, tj. izvan skupa A nema ničega. To se na Vennovom dijagramu prikazuje tako da se područje izvan A iscrtka. Naime, Venn iscrtkavanjem područja označava da je ono prazno.

­­

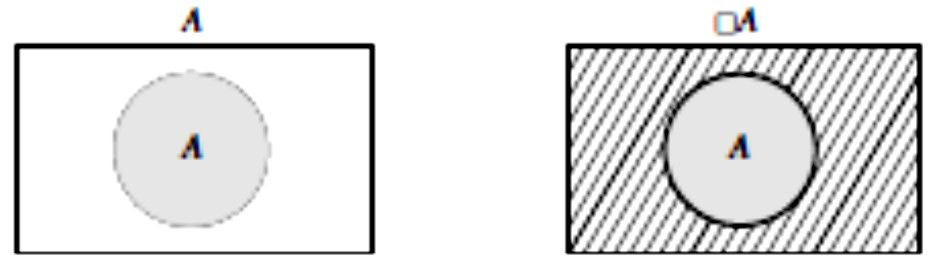
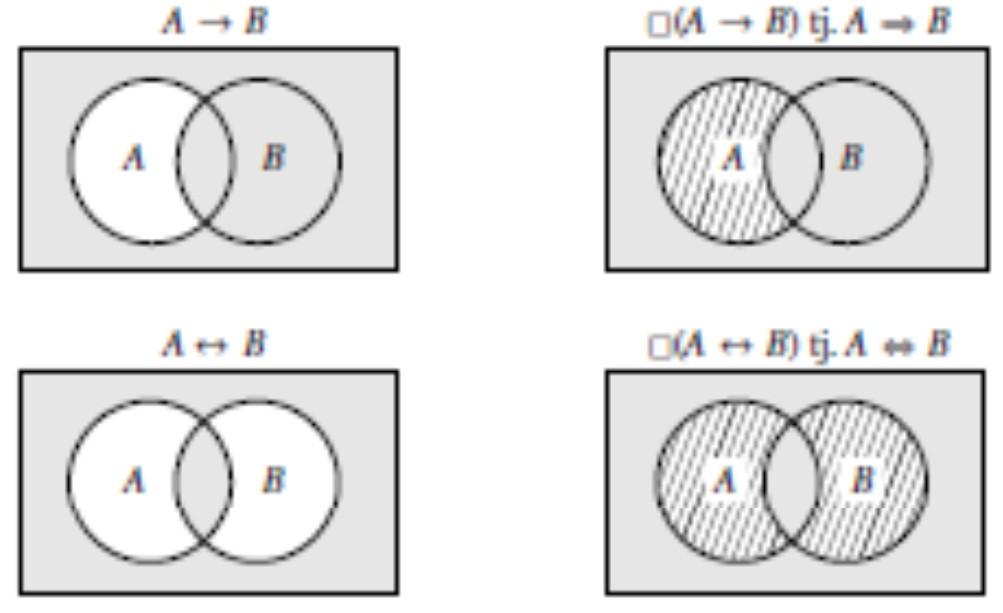
Lijevi Eulerov dijagram prikazuje jedan objekt (formu A), a desni Vennov dijagram prikazuje tvrdnju o tom objektu (da je forma A valjana, jer je sve izvan područja A prazno). To je ona ista razlika koju smo uočili između kondicionala i implikacije, te bikondicionala i ekvivalencije.

Sljedeći Eulerovi dijagrami, koji su lijevo, prikazuju kondicional i bikondicional, dok desni Vennovi dijagrami prikazuju implikaciju i ekvivalenciju.

­­

Razmotrimo, nadalje, što znači da je forma A konzistentna. To znači da postoji interpretacija u kojoj je ona istinita, tj. da skup A nije prazan. To se na Vennovom dijagramu prikazuje tako da se u područje A stavi križić ×. Dakle, stavljanjem križića × u neko područje Venn označava da ono nije prazno. Lijevi Eulerov dijagram opet prikazuje objekt (formu A), dok desni Vennov dijagram prikazuje tvrdnju o tom objektu (da je forma A konzistentna, jer je unutar područja A križić).

­­

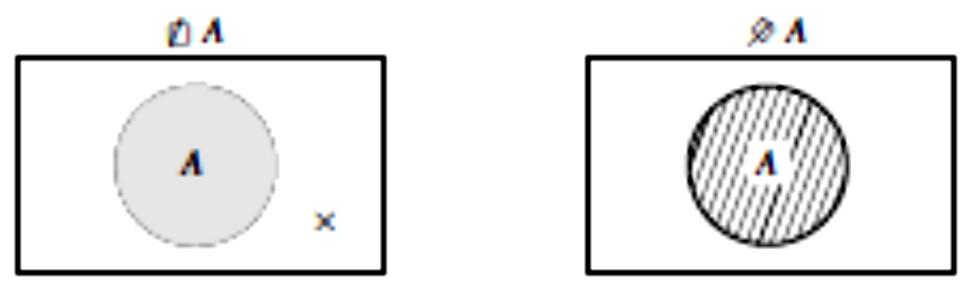
U skladu s Vennovom konvencijom nevaljanost forme A prikazuje se križićem, kao lijevo dolje, a inkonzistentnost forme A iscrtkavanjem, kao desno dolje.

­­

U jednom od sljedećih nastavaka vidjet ćemo kako ove Vennove konvencije uspješno rješavaju probleme Aristotelove silogistike.

3. Generalizirana implikacija i Gentzenov sustav dokazivanja

Ključni logički pojmovi implikacije, konzistentnosti i valjanosti, posebni su slučajevi pojma generalizirane implikacije. Veći dio ovog odjeljka posvetit ćemo terminologiji i simbolizaciji vezanoj uz taj pojam.

DEFINICIJA GENERALIZIRANE IMPLIKACIJE

Skup formi Γ (generalizirano) implicira skup formi Δ ako ne postoji interpretacija u kojoj su sve forme iz Γ istinite i sve iz Δ neistinite. Dakle, u svakoj interpretaciji bar jedna forma iz Γ prima vrijednost ⊥ ili bar jedna forma iz Δ prima vrijednost ⊤.

To simbolički zapisujemo Γ ⊨ Δ i čitamo “Γ (generalizirano) implicira Δ”.

Složena forma oblika Γ ⊨ Δ zove se sekventa. Forme iz Γ zovu se njenim premisama, a forme iz Δ njenim konkluzijama.

Skupove Γ i Δ zapisujemo kao liste koje odvajamo zarezima. Npr. {A, B, A} ⊨ {C, D} zapisujemo A, B, A ⊨ C, D ili A, B ⊨ D, C  jer je {A, B, A} = {A, B} i {C, D} = {D, C}. Umjesto praznog skupa ∅ ne pišemo ništa. Dakle, Γ ⊨ ∅ zapisujemo Γ ⊨ , ∅ ⊨ Δ zapisujemo ⊨ Δ.

Ako je Γ ≠ ∅ i Δ sadrži točno jednu formu onda Γ ⊨ Δ i Γ ⇒ Δ znače isto jer im se definicije poklapaju. U oba slučaja nema interpretacije u kojoj bi sve forme iz Γ bile istinite, a u kojoj bi forma Δ ipak bila neistinita. Relacija ⊨ je općenitija jer dopušta da su Γ i Δ proizvoljni skupovi.

Na primjer, Γ ⊨ znači da nema interpretacije u kojoj su sve forme iz Γ istinite. To znači da je Γ inkonzistentan skup formi. ⊨ A znači da nema interpretacije koja formu A čini neistinitom, tj. forma A je valjana. Ako su Γ = {A, … , B } i Δ = {C, … , D } konačni skupovi formi onda se relacija ⊨ može svesti na relaciju ⇒ koja povezuje samo dvije forme. Naime, interpretacija u kojoj su sve A, … , B istinite forme, a sve C, … , D neistinite forme ujedno je i interpretacija u kojoj je A ∧ … ∧ B  istinita forma, a C ∨ … ∨ D neistinita.

TEOREM O KONZISTENTNOSTI KAO GENERALIZIRANOJ IMPLIKACIJI

⟐Γ znači isto što i Γ ⊭.

TEOREM O VALJANOSTI KAO GENERALIZIRANOJ IMPLIKACIJI

⊡ A znači isto što i ⊨ A.

TEOREM O SVOÐENJU GENERALIZIRANE IMPLIKACIJE NA OBIČNU

A, … , B ⊨ C, … , D znači isto što i A ∧ … ∧ B ⇒ C ∨ … ∨ D.

Implikacija ⊨ pokorava se strukturnim pravilima  koja vrijede za sve forme kojima ćemo se baviti, a ne samo za IF–forme.

DEFINICIJA STRUKTURNIH PRAVILA

­­­ ­

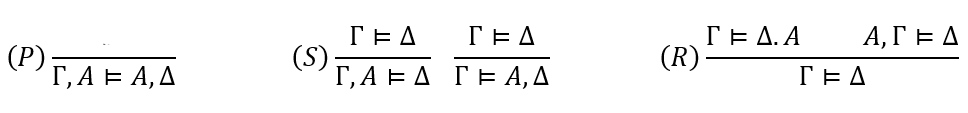
Γ, A ⊨ A, Δ uvijek je istinito, jer ne postoji interpretacija u kojoj bi A mogla biti i istinita i neistinita. To se pravilo zove “preklapanje” jer se skupovi premisa Γ, A i konkluzija A, Δ preklapaju (bar u A). Crta iznad Γ, A ⊨ A, Δ iznad koje nema sekventi, znači da je to pravilo koje nema pretpostavki, tj. to je aksiom.

Ako vrijedi Γ ⊨ Δ, tj. ako ne postoji interpretacija u kojoj su svi Γ istiniti i svi Δ neistiniti, onda ne postoji ni interpretacija u kojoj su svi Γ, A istiniti i svi Δ neistiniti, tj. iz Γ ⊨ Δ slijedi Γ, A ⊨ Δ. Slično, iz Γ ⊨ Δ, slijedi i Γ ⊨ A, Δ. To se pravilo zove “slabljenje” jer su Γ, A ⊨ Δ i Γ ⊨ A, Δ očito slabije implikacije od Γ ⊨ Δ.

Zadnje strukturno pravilo je poopćena verzija tranzitivnosti implikacije. Ono možda nije sasvim očito. Pretpostavimo, međutim, da ono ne vrijedi, tj. da imamo:

­­

Tada bi, u skladu s (3), postojala interpretacija u kojoj su svi Γ istiniti i svi Δ neistiniti. U toj interpretaciji forma A je ili istinita ili neistinita. U prvom slučaju smo u kontradikciji s (2), a u drugom s (1). U svakom slučaju dolazimo do kontradikcije, tj. naše pravilo ipak vrijedi. To se pravilo zove “rez” jer je forma A “izrezana” u konačnom zaključku.

Osim strukturnih pravila, u IF–logici vrijede i posebna pravila čija korektnost slijedi iz definicije odgovarajućih IF–veznika. Ona zajedno sa strukturnim pravilima čine Gentzenov klasični IF-sustav dokazivanja.

PRAVILA GENTZENOVOG SEKVENTNOG IF-SUSTAVA

­­

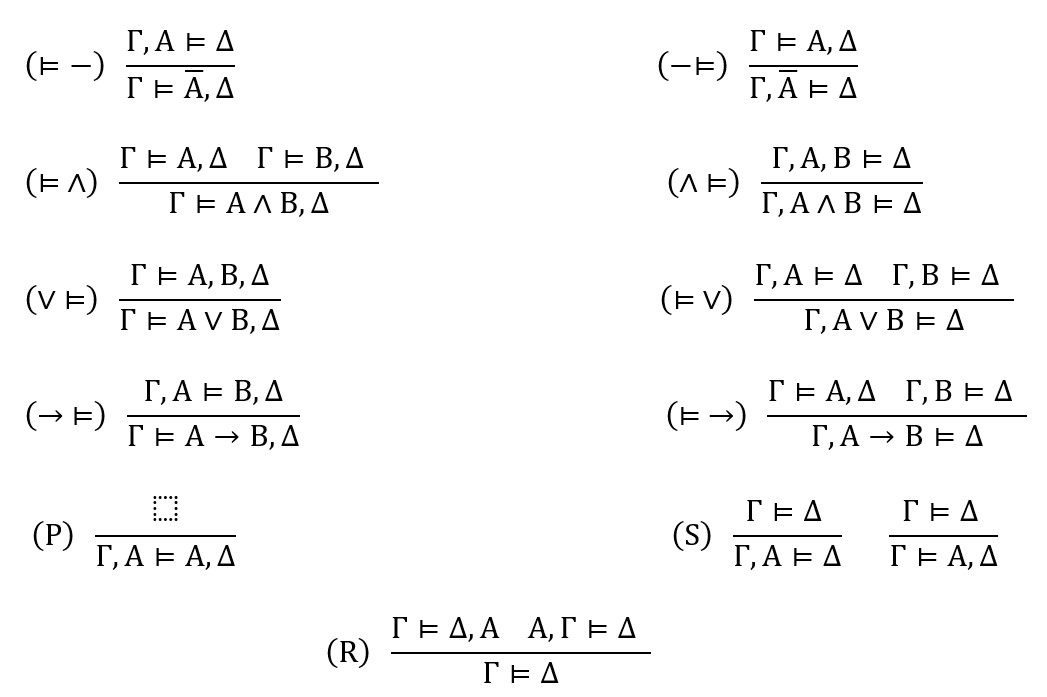
Na primjer, lako se vidi da vrijedi (⊨ ∧), tj. da iz (1) i (2) slijedi (3).

­­

Naime, ako vrijede (1) i (2) to znači da je u svakoj interpretaciji bar jedna forma u Γ neistinita ili je bar jedna forma u Δ istinita ili su obje forme A i B istinite. U sva tri slučaja vrijedi (3). Na sličan način se dokazuju i ostala pravila.

Uočimo da svaki IF–veznik ima po dva pravila. Lijevim se pravilom veznik uvodi lijevo od ⊨.  Desnim se pravilom veznik uvodi desno od ⊨.  U skladu s tim su pravila i označena. Uvođenje veznika uobičajeno je zvati njegovom introdukcijom.

Sekventa Γ ⊨ Δ dokaziva je u Gentzenovom sekventnom sustavu ako se može izvesti pomoću njegovih pravila (tj. može se izvesti iz preklapanja, kao aksioma, uz pomoć ostalih pravila). U sljedeća dva primjera u Gentzenovom sustavu dokazujemo

\(\small \neg (\overline{P} \land Q) \models P \vee \overline{Q}\) i \(\small (P \land Q) \vee (P \land R) \models P \land (Q \vee R)\).

­­

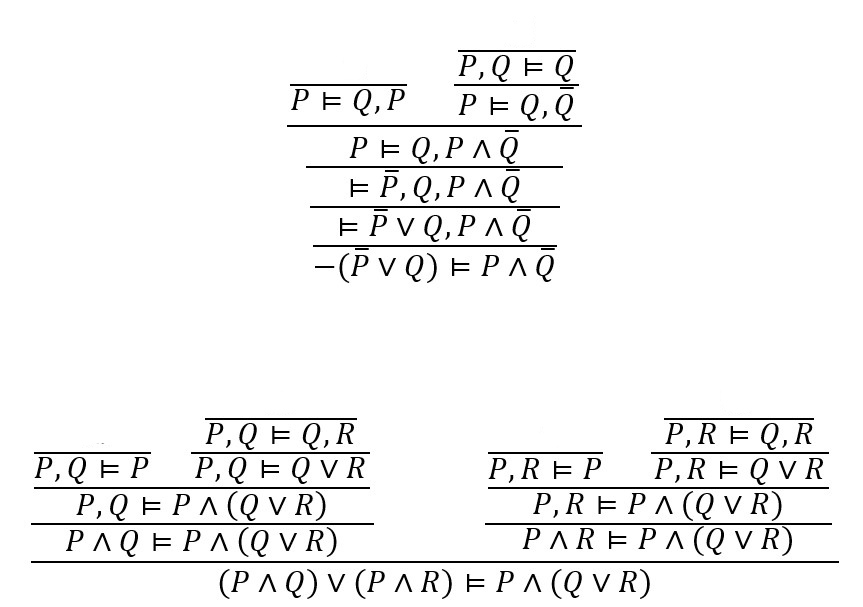
Pravila koja smo do sada uveli samo su maleni (iako sistematični) izbor iz skupa svih korektnih pravila dokazivanja IF-sekventi. Ipak, uskoro ćemo dokazati da sve istinite IF-implikacije slijede iz našeg izabranog skupa, tj. da je Gentzenov sustav potpun. U njemu se češće koristi simbol ⊢, a ne ⊨, da bi se naglasila razlika između sintaktičkog pojma dokazivosti i semantičkog pojma istinitosti. To da je u IF-logici ⊢ = ⊨, tj. da je sintaktička relacija ⊢ semantički potpuna, nije slučaj u svim logikama.