Novi način brojanja. Algoritam koji čita Hamleta i baca novčiće

Kada brojevi postaju preveliki, brojanje postaje aproksimativno, bez obzira radi li se o životinjama ili ljudima, ili o realnim brojevima zapisanim u arhitekturi računala, piše Aleksandar Hatzivelkos. Nedavno otkriveni CVS algoritam omogućava jednostavnu no dosta preciznu aproskimaciju, uz minimalno korištenje resursa.

• Naslovna fotografija: Masa zelenih brojeva na crnom ekranu u obliku Hamleta s lubanjom. (Midjourney v7)

• Autor je matematičar i profesor stručnog studija na Veleučilištu Velika Gorica. Politički je aktivan u sklopu stranke Možemo od 2019. godine.

Proces brojanja je neodvojiv od povijesti ljudskog roda. Neki od najstarijih ljudskih artefakata, poput „Vučje kosti“ stare 26 000 godina pronađene u današnjoj Češkoj ili „Lebombo kosti“ stare 40 000 godina u Južnoj Africi, imaju ureze koji se interpretiraju kao bilježenje prebrajanja. Štoviše, znanost pokazuje kako brojanje nije ekskluzivno za ljudski rod. Eksperimenti pokazuju kako mnoge životinje razumiju i koriste brojanje. Neuropsiholog Brian Butterworth zastupa tezu kako je „osnovna ideja o broju prirodno urođena većini, ako ne i svim životinjama, te se kroz životno iskustvo i upotrebu modificira prema potrebama određene vrste“.[1] Tako bez zadrške možemo reći kako nas koncept brojanja prati od samih početaka, čak i prije nego smo se identificirali kao Homo sapiensi.

Pojedine životinjske vrste mogu točno brojati i do dvadeset ili trideset. (Andreas Nieder)

Pri tome se, kod proučavanja procesa brojanja kod svih životinjskih vrsta, znanstvenici susreću s činjenicom da pojedine vrste mogu točno brojati do neke veličine tzv. sustav objektnih zapisa (eng. Object File System), koja je kod proučavanih životinja jednaka barem četiri, dok se kod nekih životinjskih vrsta (poput majmuna i vrana) penje do dvadeset ili trideset.[2] Nakon toga životinje koriste tzv. približni brojevni sustav (eng. Approximate Number System). Jednostavno rečeno – kad brojevi postanu preveliki za pojedinačno brojanje (ili mentalne kapacitete), umjesto točnih vrijednosti životinje pribjegavaju aproksimativnoj ocjeni veličine.

Brojevi i prebrojavanje su krucijalni i za modernog čovjeka. Pustimo li nastranu direktnu primjenu, poput ekonomije ili prirodnih znanosti, sva digitalna tehnologija zasnovana je na brojčanom (binarnom) zapisu informacija. Za potrebe ovog članka, pažnju ćemo posvetiti jednom specifičnom načinu zapisivanja realnih brojeva, koji računala oko nas koriste svake sekunde, zapisu broja u tzv. aritmetici pomičnog zareza (floating point aritmetici).

Krenut ćemo od pretpostavke da su čitatelji upoznati s konceptom binarnog zapisa broja, koji nam omogućava da svaki realni broj možemo zapisati kao (ne nužno konačan) zbroj (pozitivnih i negativnih) potencija broja 2. Tako se primjerice broj 40.5625 zapisan u dekadskom zapisu, u binarnom zapisu zapisuje 101000.1001. No taj zapis nije finalni zapis u aritmetici pomičnog zareza – cilj nam je broj zapisati na način da decimalnu točku (ili po pravopisu „decimalni zarez“) postavimo odmah nakon prve znamenke: 1.010001001 · 2⁵. Baš kao što pomicanje decimalne točke u dekadskom zapisu predstavlja množenje ili dijeljenje s potencijama broja 10, tako pomicanje točke u binarnom zapisu predstavlja množenje, odnosno dijeljenje broja s potencijama broja 2.

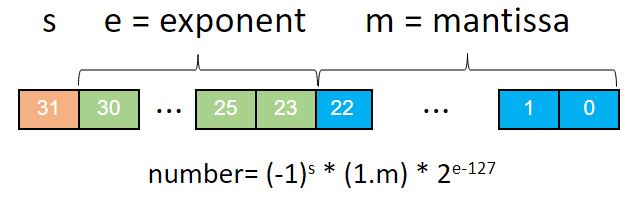
U takvom zapisu, pomicanjem decimalne točke osiguravamo da se ona uvijek nalazi neposredno iza prve znamenke 1, pa tu jedinicu nema potrebe pamtiti. Stoga u memoriji pohranjujemo dvije vrijednosti: tzv. mantisu, odnosno dio broja koji se nalazi nakon decimalne točke i eksponent (na broju 2).[3] U navedenom primjeru mantisa bi bila jednaka 010001001, a eksponent 101 (odnosno 5). Računalni standard IEEE754 u zapisu broja u dvostrukoj preciznosti (64-bitni zapis) tako osigurava 52 bita za zapis mantise, 11 bita za zapis eksponenta, dok  se u jednom bitu pohranjuje informacija o predznaku broja.

Zapis brojeva u takvom formatu nudi prilično gustu strukturu u kojoj je moguće zapisati brojeve u rasponu 4.94 · 10^-324 do 1.80 · 10³⁰⁸. Za potrebe ovog teksta istaknut ćemo dva svojstva ovakvog zapisa brojeva:

2. Radi se o skupu s konačno mnogo vrijednosti. Iako možemo zapisati izrazito velik broj različitih brojeva, ipak se radi o konačno mnogo vrijednosti. Što znači da je tek konačan broj točaka s brojevnog pravca moguće točno zapisati, dok za (neprebrojivo) beskonačno mnogo vrijednosti zapravo zapisujemo aproksimaciju, odnosno najbližu točku iz ponuđenog skupa vrijednosti koje je moguće zapisati.
3. Razmaci između brojeva koje možemo točno zapisati rastu s veličinom vrijednosti koje zapisujemo. Na primjer, razmaci između brojeva koje je moguće zapisati, a čija se veličina kreće oko 1 iznosi 2.2 · 10^-16; razmaci između brojeva reda veličine 2⁵² (odnosno 4 500 000 000 000) iznosi 1; dok razmaci između najvećih brojeva koji se mogu zapisati u aritmetici pomičnog zareza s dvostrukom preciznošću iznose 2⁹⁷¹. Poanta je da kod zapisivanja brojeva u računalu koristimo aproksimaciju, odnosno najbliži mogući broj koji je u danoj aritmetici moguće zapisati, pri čemu izraz „najbliži mogući“ može predstavljati enormne udaljenosti.

To nas konačno vodi do teme ovog članka – što povezuje priču o zapisivanju brojeva u računalu i priču o elementarnom brojanju koje nalazimo i kod životinja? Odgovor je, kako je to pomalo senzacionalistički nazivano – novi način brojanja.

Autori CVM algoritma: Sourav Chakraborty, Vinodchandran Variyam i Kuldeep S. Meel.

Proteklih nekoliko godina pojavilo se nekoliko članaka koji, temeljeći se na članku Distinct Elements in Streams: An Algorithm for the (Text) Book matematičara S. Chakrabortyja, N. V. Vinodchandrana i K. S. Meela, pišu o otkriću novog načina brojanja. Takav naslov je pomalo zavaravajući. Ne radi se naravno, o novom načinu brojanja, već o novom algoritmu koji aproksimira rezultat brojanja u određenim okolnostima.

Krenimo redom.

U računarstvu je dobro poznat Problem broja različitih vrijednosti (eng. Distinct Elements Problem). Radi se o problemu prebrojavanja različitih vrijednosti u nekom skupu (ili nizu) podataka – klasičan primjer bi bio prebrajanje broja različitih riječi u nekom književnom djelu, na primjer Hamletu.

Za Problem broja različitih vrijednosti postoji više algoritama koji ga rješavaju. Na primjer, ako se radi o brojčanim vrijednostima ili nekom skupu podataka na kojemu postoji linearni uređaj (na primjer, riječima kod kojih je uređaj definiran poretkom slova u abecedi), elemente je moguće sortirati, pa iz poredanog niza podataka pobrisati sve ponavljajuće elemente.

Drugi efikasniji algoritam elemente iz skupa (jednog po jednog) prepisuje u posebni memorijski prostor (na primjer, po veličini ili abecedi), pri čemu kod prepisivanja provjerava je li taj element već upisan. Ako jest, tada ga preskače i ne upisuje. Na kraju je potrebno samo prebrojati zapisane elemente.

Kao primjer, brojimo različite riječi koje se pojavljuju u Hamletu. (Folger Shakespeare Library / CC BY-SA 4.0)

Navedeni algoritam možemo vizualizirati na sljedeći način. Recimo da želimo prebrojati broj različitih riječi koje se pojavljuju u Shakespeareovom Hamletu. Krenemo kroz knjigu riječ po riječ, i svaku novu riječ prepisujemo na ploču. Pri tome riječi na ploči zapisujemo po abecednom redu (na primjer, u prvom stupcu riječi koje počinju sa slovom A, u drugom sa slovom B itd.) kako bi ih lakše pretraživali. Ako je riječ već zapisana na ploči, preskačemo je i prelazimo na sljedeću riječ u knjizi. Kada prođemo kroz sve riječi u knjizi, prebrojimo koliko smo riječi zapisali na ploču.

Sam algoritam je jednostavan i široko korišten. Problem broja različitih vrijednosti često se pojavljuje u suvremenom svijetu: streaming servisima je potrebna informacija o broju unikatnih gledalaca, društvenim mrežama informacija o broju unikatnih logiranja, u prodajnim statistikama važna je informacija o broju tipova prodanih proizvoda… I gotovo svi navedeni primjeri imaju jednu zajedničku karakteristiku – radi se o prebrajanjima jako velikog broja unikatnih elemenata u još većem broju informacija.

Kraće rečeno, za rješavanje problema broja različitih vrijednosti potrebna nam je jako, jako velika ploča – odnosno memorija.

Zamislimo stoga da je i dalje potrebno riješiti isti problem, npr. prebrojati broj unikatnih riječi u Hamletu, ali da na raspolaganju imamo ograničenu memoriju. Recimo da imamo ploču na koju možemo zapisati samo stotinu riječi. Kako u tom slučaju doći do broja, ili barem dobre aproksimacije traženog broja unikatnih riječi? Upravo tim problemom se bavi algoritam o kojemu danas pišemo, CVM algoritam.[4]

Kako, dakle, radi CVM algoritam?

Opišimo njegovo djelovanje na dosada opisivanom primjeru koji su i autori koristili kao ilustraciju: prebrojavanju broja riječi u Hamletu pomoću ploče na koju je moguće zapisati stotinu riječi.

1. Postupak započinje kao i ranije: prolazimo redom kroz riječi zapisane u Hamletu, te svaku novu riječ zapisujemo na ploču, dok ponovljene riječi preskačemo.[5] Kada smo ploču popunili sa stotinu riječi, za svaku od tih riječi bacimo novčić (ili provedemo neki drugi slučajni eksperiment u kojemu oba ishoda imaju vjerojatnost pojavljivanja); ako je pala glava riječ ostavimo zapisanu na ploči, a ako je palo pismo riječ pobrišemo s ploče. Nakon tog brisanja, ostat će nam ploča s približno pedeset zapisanih riječi. Ovaj prvi korak zovemo Krug 0.
2. Sada prelazimo na fazu koju autori zovu Krug 1. Nastavimo prolaziti kroz tekst Hamleta, te nove riječi zapisujemo na ploču, no sada prije zapisivanja riječi na ploču bacimo novčić: ako dobijemo glavu, riječ zapisujemo na ploču, a ako dobijemo pismo, ne. No ako naiđemo na riječ koja se već nalazi na ploči, postojeću riječ pobrišemo, te potom opet bacimo novčić da li ćemo je (ponovno) zapisati – ako je pala glava riječ ponovno zapišemo na ploču, a ako je palo pismo mjesto ostavljamo praznim. I tako sve dok opet ne popunimo ploču. Kada popunimo ploču, za sve riječi bacamo novčić hoćemo li ih zadržati na ploči ili ne. Tako da na kraju Kruga 1 ploča opet otprilike polovično popunjena.
   Poanta postupka je da sve riječi koje se nalaze zapisane na ploči na kraju Kruga 1 imaju vjerojatnost \(\small \frac{1}{2}\) da će se nalaziti na ploči – za sve riječi koje smo upisali na ploču u Krugu 1 smo bacali novčić da li ćemo ih zapisati ili ne. S druge strane, riječi koje su prije Kruga 1 došle na ploču su „preživjele“ globalno brisanje s vjerojatnošću \(\small \frac{1}{2}\) na kraju Kruga 0.
3. Slijedi Krug 2. Postupak je sličan, prolazimo kroz Hamleta, te nove riječi zapisujemo na ploču, no sada prije upisivanja riječi na ploču novčić bacamo dva puta, te ga zapisujemo na ploču jedino ako u oba bacanja padne glava (dakle s vjerojatnošću \(\small \frac{1}{2^2}\)). Kod ponovljenih riječi, baš kao i u Krugu 1, riječ prvo pobrišemo, pa potom bacamo novčić dva puta kako bi odlučili da li ćemo je zapisati. Dakle, vjerojatnost da ta riječ ostane na ploči nakon Kruga 2 iznosi \(\small \left(\frac{1}{2}\right)^2 = \frac{1}{2^2}\). Ili je riječ upisivana u ovom krugu, pa zbog bacanja dviju kockica ima tu vjerojatnost pojavljivanja, ili je prenesena iz prethodnog kruga (u kojemu je imala vjerojatnost pojavljivanja \(\small \frac{1}{2}\)), te je „preživjela“ globalno brisanje na kraju Kruga 1, opet s vjerojatnošću \(\small \frac{1}{2}\). Na kraju, po popunjavanju ploče, za sve riječi opet bacamo kockicu ostaju li na ploči ili ne, te prelazimo na Krug 3.
4. Općenito, postupak se ponavlja kroz k krugova, sve dok ne iscrpimo sve riječi iz Hamleta, s napomenom da u k-tom krugu, prije upisivanja nove riječi na ploču, novčić bacamo k puta, te riječ zapisujemo na ploču jedino ako su u svih k bacanja pale glave. Kao i u prethodnim koracima u slučaju ponovljene riječi, riječ prvo brišemo s ploče, pa potom provodimo proceduru upisa nove riječi. Zbog toga je na kraju Kruga k vjerojatnost pojavljivanja svake zapisane riječi na ploči \(\small \left(\frac{1}{2}\right)^k = \frac{1}{2^k}\).

S algoritmom stajemo kad prođemo kroz sve riječi zapisane u Hamletu, što će se dogoditi u nekom Krugu n. Zbog konstrukcije algoritma, svaka riječ koja će u tom trenutku biti zapisana na ploči ima vjerojatnost pojavljivanja \(\small \frac{1}{2^n}\).

Konačno, iz frekvencijske aproksimacije vjerojatnosti događaja znamo kako je \(\small p \approx \frac{m_1}{m}\), gdje je m₁ broj riječi zapisanih na ploči, a m broj unikatnih riječi u knjizi Hamlet.[6] Odavde jednostavno slijedi aproksimacija za ukupan broj unikatnih riječi u Hamletu:

\( m \approx \frac{m_1}{p} = \frac{m_1}{\left(\frac{1}{2^n}\right)} = m_1 \cdot 2^n\),

pri čemu je m₁ broj riječi zapisanih na ploči na kraju algoritma, a n broj krugova (popunjavanja ploče) kroz koje smo prošli u izvođenju algoritma.

U konkretnom primjeru koji se bavi prebrajanjem broja unikatnih riječi u knjizi Hamlet, autori navode kako knjiga Hamlet sadrži 3967 unikatnih riječi.[7] Prvo provođenje algoritma rezultiralo je s 61 riječi zapisanom na ploči (m₁ = 61) i zaustavljanjem algoritma na šestom krugu (n = 6). Prema tome, aproksimacija broja unikatnih riječi bi bila:

\(\small m \approx m_1 \cdot 2^n = 61 \cdot 2^6 = 3904\).

Prosječna aproksimacija nakon pet izvođenja algoritma je bila 3955, dok je prosječna aproksimacija pet izvođenja s memorijom (pločom) koja pohranjuje 1000 riječi iznosila 3964. Općenito, točnost procjene ovisi o veličini dostupne memorije: što više memorije algoritam smije koristiti, to će njegova procjena biti bliža stvarnom broju jedinstvenih elemenata. Autori su dokazali da je CVM algoritam optimalan, što znači da postiže najbolju moguću točnost za zadanu količinu memorije. Prijašnji rezultati u tom području postavili su donju granicu (minimalnu količinu memorije) potrebne za rješavanje problema broja različitih vrijednosti,[8] dok su ovim člankom autori dokazali da CVM algoritam koristi točno tu razinu memorije.

Na kraju treba istaknuti kako je u ovom tekstu algoritam opisan kroz mehanizam slučajnog odabira koji je poznat širokoj publici, odnosno pomoću bacanja novčića. Naravno, u samom algoritmu se ne bacaju novčići već se slučajni događaji realiziraju kroz generator pseudoslučajnih brojeva, funkciju koja je ugrađena u praktički svaki programski jezik i oslanja se na temeljne operacije samog procesora.

Također, algoritam ima optimiziran način upotrebe generiranja slučajnih događaja. Na primjer u trećem krugu izvođenja nećemo tri puta generirati slučajne događaje s vjerojatnošću 0.5 (što bi bio neposredni ekvivalent bacanja tri novčića), već ćemo slučajni događaj generirati samo jednom, no s vjerojatnošću 0.125.

Sam algoritam je izrazito jednostavan ali i genijalan

Nakon što smo vidjeli o kakvom se „novom načinu brojanja“ radi, red je da se vratimo do početka ovog teksta. Kakve veze CVM algoritam ima sa sposobnošću životinja da broje ili načinom na koji zapisujemo (aproksimiramo) realne brojeve u arhitekturi računala?

Začuđujuće, vrlo velike.

Prisjetimo li se kako je opisan način na koji životinje broje: do nekog mjesta brojanje se provodi egzaktno, no kada brojevi postanu „preveliki“ (pri čemu ta granica varira od vrste do vrste) brojanje postaje aproksimativno.

Sličan razvoj situacije vidimo i kod problema broja različitih vrijednosti – dok je broj različitih elemenata mali, ili dok je memorija koja nam je na raspolaganju dovoljno velika (gdje možemo povući paralelu s biološkim kapacitetom za brojanje kod životinjskih vrsta), brojanje različitih elemenata provodimo eksplicitno. No kod „prevelikih“ skupova podataka,[9] CVM algoritam nam daje mogućnost aproksimiranja tih veličina.

Kao i kod brojeva u dvostrukoj preciznosti, “mreža” brojeva u koju uklapamo aproksimaciju postaje sve rjeđa s porastom vrijednosti koju aproksimiramo.

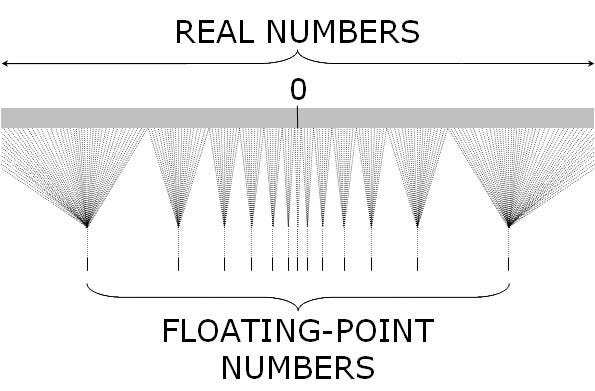
S druge strane, struktura te aproksimacije ima mnogo zajedničkog sa zapisivanjem (aproksimacije) realnih brojeva u dvostrukoj preciznosti. U oba slučaja postoji konačna „mreža“ brojeva u koju uklapamo aproksimaciju.

Već smo opisali kako ta „mreža“ brojčanih vrijednosti izgleda kod zapisivanja realnih brojeva u računalu. Kod aproksimacije koju nam daje CVM algoritam radi se o mreži brojeva sačinjenoj od (konačnog broja) višekratnika broja 2ⁿ, gdje je n broj krugova (u CVM algoritmu) u kojemu se iscrpi niz elemenata čije unikatne članove prebrajamo. Baš kao i kod brojeva u dvostrukoj preciznosti ta mreža postaje sve rjeđa s porastom vrijednosti koju aproksimiramo, no relativna greška aproksimacije u odnosu na veličinu broja ostaje na istoj razini.[10]

Na neki način sam algoritam je izrazito jednostavan ali i genijalan. Manjak prostora nadoknađuje uzorkovanjem (sempliranjem) podataka u kojemu vjerojatnost koristi kao vrstu koda za pozicioniranje aproksimacije u konačno velikoj mreži odgovarajuće veličine. I neposredno nam daje mogućnost za proces koji (barem) životinje koriste već milijunima godina – kada stvari postanu prevelike da se prebroje, aproksimiramo njihovu veličinu.

• Bilješke

[1] Brian Butterworth je autor knjige „Can Fish Count“, dok su njegovi rezultati, kao i recentni rezultati drugih znanstvenika na temu brojanja kod životinja sumirani u članku Philipa Huntera „Animals do count“, EMBO rep (2022) 23, doi: 10.15252/embr.202255511

[2] Vidi npr. Benson-Amram S., Gilfillan G. i McComb K., Numerical assessment in the wild: insights from social carnivores, Philosophical Transactions of the Royal Society B (2018), doi: 10.1098/rstb.2016.0508

[3] Potpune preciznosti radi, pamte se tri veličine: pored mantise i eksponenta u jednom bitu se pohranjuje informacija o predznaku.

[4] Algoritam je nazvan CVM algoritmom prema početnim slovima prezimena autora: Chakraborty, Vinodchandran i Meel.

[5] Preciznosti radi, u „nultom koraku“, tj. prije nego li je ploča prvi puta popunjena, kod pojavljivanja ponovljene riječi, algoritam briše već zapisanu riječ i ponovno upisuje tu istu riječ s vjerojatnošću , dakle uvijek.

[6] Frekvencijska aproksimacija vjerojatnosti je metoda procjene stvarne vjerojatnosti nekog događaja promatranjem koliko se često taj događaj dogodio u velikom broju ponovljenih pokusa. Klasično se pojam vjerojatnosti događaja u nastavi uvodi upravo putem frekvencijske aproksimacije kada se vjerojatnost definira kao broj povoljnih događaja podijeljen s ukupnim brojem događaja.

[7] Vidi Delahaye, J. “L’algorithme oublié.” Pour la Science, br. 561, (srpanj 2024.), str. 80-85. ili Nadis, S. (svibanj 2024). Computer scientists invent an efficient new way to count. Quanta Magazine. https://www.quantamagazine.org/computer-scientists-invent-an-efficient-new-way-to-count-20240516/

[8] Vidi Kane, D. M., Nelson, J., & Woodruff, D. P. (2010). An optimal algorithm for the distinct elements problem. In Proceedings of the twenty-ninth ACM SIGMOD-SIGACT-SIGAI symposium on Principles of database systems (pp. 41–52). Association for Computing Machinery. Doi: 10.1145/1807085.1807094

[9] Ovog puta „preveliki“ zapravo označava veličine kod kojih eksplicitno prebrojavanje postaje vremenski ili memorijski neefikasno, odnosno kada memorijski ili vremenski resursi potrebni za rješavanje problema postanu znatan trošak u odnosu na korist dobivenu od informacije.

[10] Ta je relativna greška u samom članku označena s , a radom se pokazuje i statistička razina značajnosti očekivane relativne greške, koja je označena s .