Propozicijske, monadske i poliadske forme. Kvantifikacija i prirodni jezici

U razradi apstrakata i kvantifikacije, Zvonimir Šikić pokazuje kako se složene tvrdnje prevode u predikatske forme, uvodi pravila prolaza kvantifikatora te dokazuje ekvivalentnost i odlučivost monadske logike, dok ističe da su poliadski predikati izražajniji i da redoslijed kvantifikatora tada postaje presudan.

• Naslovna fotografija: Crtež Gottfrieda Leibnitza kredom na ploči. (Midjourney v7)

• Prethodni članci u seriji: Bulovska logika pojmova. Forme, strukture i implikacije, Aristotelova silogistika. Jednostavna i jedina simbolička logika kroz dva milenija, Formalizacije logike sudova. Frege i Kneale, generatori i testovi, Logička korektnost, potpunost i kompaktnost. Gentzenov IF-sustav i Bethova semantička stabla, Zaključivanje u prirodnom i artificijelnom jeziku. Od Aristotela prema Fregeu, Logika sudova. Kondicionali, bikondicionali i implikacije

­

1. Apstrakti i kvantifikacija

U prirodnim jezicima opće pojmove možemo izraziti imenicama, pridjevima, glagolima itd. (usp. početne primjere u prethodnom poglavlju). Frege je, u drugoj polovici 19. st., ukazao na to da svaku tvrdnju o nekom objektu možemo shvatiti kao predikaciju nekog općeg pojma tom objektu; čak i onda ako je tvrdnja izrazito složena i ne izražava taj pojam jednostavnom imenicom, pridjevom, glagolom itd. Promotrimo sljedeću tvrdnju:

Petar se posvađao s Lukom jer je Luka bio u vezi sa ženom njegovog mlađeg brata.

Na prvi pogled nije jasno koji je pojam prediciran Petru u toj tvrdnji. Ipak prirodni jezici imaju sredstvo za izgradnju takvih pojmova. To su relativne rečenice (koje bi točnije bilo zvati relativnim pojmovima). U našem slučaju:

onaj koji se posvađao s Lukom jer je Luka bio u vezi sa ženom njegovog mlađeg brata

U logici zamjenice onaj, koji, ovaj itd. označavamo s x, y, z itd. i zovemo ih varijablama. Tako naša relativna rečenica postaje nešto jasnijom:

x takav da se x posvađao s Lukom jer je Luka bio u vezi sa ženom x-ovog mlađeg brata

(npr. sada je jasnije na koga se odnosi “njegov” iz prethodne formulacije).

Složen opći pojam “x takav da …x …“, koji je dobiven iz rečenice “…x …“, u logici zovemo apstraktom i označavamo ga s [x: …x …]. Ako je rečenica “…x …” jednostavna imenska, pridjevska ili slična predikacija, onda apstrakt postaje nepotrebno složeni ekvivalent jednostavnog imenskog, pridjevskog ili sličnog pojma. Na primjer, [x:x je logičar] = logičar, [x:x je lijep] = lijep itd.

Ako apstrakt prediciramo nekom objektu dobivamo tvrdnju koja je ekvivalentna početnoj tvrdnji o tom objektu. Na primjer, “Petar je x takav da se x posvađao s . . . ” ekvivalentna je tvrdnji “Petar se posvađao s …“; ili općenito:

[x: …x …]a ⇔ …a …

(Predikacija pojma P objektu a koja se označava s Pa, katkada se označava s a ∈ P i tada vrijedi ekvivalencija: a ∈ [x∶ …x …] ⇔ …a… . Primijetimo da je ∈ kopula koja veže singularni pojam (tj. individuu a) s općim pojmom P; za razliku od kopula ⊆ i = koje vežu opće pojmove. Primijetimo nadalje da kopula ∈, kako je ovdje koristimo, ima značenje potpuno određeno prethodnom ekvivalencijom. To znači da apstrakt može biti samo desno od kopule ∈, dok lijevo od nje nema značenje. Tek teorija skupova daje značenje izrazima oblika [x: …x …] ∈ P, pretvarajući apstrakte iz općih pojmova u singularne, tj. u individue. Time teorija skupova prelazi okvire logike. Ako baš želimo i u logici apstrakte zvati skupovima onda je to Quineov virtualni govor o skupovima, kojem je svo značenje sadržano u gornjoj ekvivalenciji.)

Rečenice oblika “…x …“, koje na mjestima za imena sadrže varijable (tj. zamjenice), zovemo otvorenim rečenicama. One se razlikuju od zatvorenih rečenica po tome što nisu ni istinite ni neistinite. One su istinite ili neistinite ovisno o tome što je x.

Otvorene rečenice možemo zatvoriti na više načina. Najjednostavniji je supstitucija imena na mjesto varijable; npr. tako višeznačna otvorena rečenica “x se posvađao s …” prelazi u jednoznačnu zatvorenu rečenicu “Petar se posvađao s …“. Drugi je način apstrakcija pojma iz otvorene rečenice; tako na primjer višeznačna otvorena rečenica “x se posvađao s …” prelazi u jednoznačni pojam [x: x se posvađao s …]. Sam pojam [x: …x …] više ne ovisi o x pa kažemo da je varijabla x vezana u apstraktu [x: …x …]. Da on više ne ovisi o x vidimo i po tome što mu se značenje ne mijenja ako x zamijenimo nekom drugom varijablom, npr. [x: x je logičar] = [y: y je logičar] = logičar.

Koristeći se vezom apstrakata i otvorenih rečenica lako je definirati istinosne funkcije pojmovnih formi uz pomoć standardnih istinosnih funkcija rečeničnih formi (usp. prethodna poglavlja):

–A = [x: –Ax],

A ∧ B = [x: Ax ∧ Bx],

A ∨ B= [x: Ax ∨ Bx],

A → B=[x: Ax → Bx]

i tako dalje.

Osim istinosno funkcionalnim veznicima na apstrakte (koji su pojmovi odnosno pojmovne forme) možemo djelovati operatorima ∃ i ∀ ili ih vezati operatorima ⊆ i =. Tako dobivamo rečenice odnosno rečenične forme bulovskoga tipa, kakve smo već razmatrali.

Na Fregeovom tragu, u prvoj polovici 20. st. u logici se ustalio običaj da se kao operatori koriste isključivo ∃ i ∀, tj. da na apstrakte djeluju samo ∃ i ∀:

∃ x [x: … x … ] i ∀ x [x: … x … ].

Tako ograničena upotreba apstrakta prirodno vodi k tome da ih potpuno izbacimo, jer gornje rečenične forme možemo dobiti i neposrednom primjenom operatora “∃x” i “∀x” na otvorenu rečenicu “… x …”. Tako ∃ [x∶ … x … ] postaje ∃ x (… x … ), a ∀ [x∶ … x … ] postaje ∀ x ( … x … ) i to je način kojim se koristi suvremena logika kada definira svoje kvantificirane forme.

2. Višemjesni predikati

Još važniji Fregeov korak, koji je postao ključnim korakom suvremene logike, jest pomak od monadskih pojmova (npr. “logičar”, “lijep” i “hoda”), koji su istiniti ili neistiniti o pojedinim objektima, prema poliadskim pojmovima, koje najčešće zovemo predikatima, i koji su istiniti ili neistiniti o parovima objekata, ili njihovim trojkama, četvorkama itd. Dakle, osim monadskih formi oblika Ha (koji ima rečenica “Ante hoda”), suvremena logika uzima u obzir i poliadske forme. Diadske su oblika Pab (koji ima rečenica “Ante pomaže Borisu”), triadske su oblika Pakb (koji ima rečenica “Ante posuđuje kosilicu Borisu”) itd. Promjena redoslijeda imena ili varijabli u poliadskim formama mijenja njihovo značenje; Pab i Pba na znače isto (u prvom slučaju Ante pomaže Borisu, a u drugom Boris Anti). To znači da su poliadski pojmovi istiniti ili neistiniti o uređenim parovima, trojkama, četvorkama itd.

U prirodnim jezicima predikati mogu biti glagoli, pridjevi itd. (npr. Ante pomaže Borisu; Krk je veći od Paga). Frege je, naravno, ukazao i na to da svaku tvrdnju o više objekata možemo shvatiti kao predikaciju nekog (višemjesnog) predikata tim objektima. Na primjer, našu tvrdnju:

Petar se posvađao s Lukom jer je Luka bio u vezi sa ženom Petrovog mlađeg brata.

možemo shvatiti kao predikaciju sljedećeg (2-mjesnog) predikata Petru i Luki.

x i y, takvi da se x posvađao s y jer je y bio u vezi sa ženom x-ovog mlađeg brata.

Taj predikat opet možemo zapisati u obliku apstrakta:

[xy ∶ x se posvađao s y jer … ],

koji nastaje apstrakcijom iz otvorene rečenice:

x se posvađao s y jer je y bio u vezi sa ženom x-ovog mlađeg brata.

Odbacimo li uporabu apstrakata, kako su to učinili Frege i suvremena logika, onda otvorene rečenice preuzimaju njihovu ulogu. Otvorena rečenica sa samo jednom varijablom (koja se može pojavljivati i više puta) je 1-mjesni monadski predikat ili kraće pojam koji je istinit ili neistinit o pojedinim objektima (dakle predstavlja svojstvo). Iz nje se supstitucijom jednog imena na sva mjesta na kojima se pojavljuju primjerci te jedne varijable dobije rečenica koja je istinita ili neistinita. Otvorena rečenica s dvije varijable (koje se mogu ponavljati i više puta) je 2-mjesni ili diadski predikat koji je istinit ili neistinit o uređenim parovima objekata (dakle predstavlja binarnu relaciju). Iz nje se supstitucijom uređenog para imena (tako da se prvo ime supstituira na mjesta svih primjeraka prve varijable, a drugo na mjesta svih primjeraka druge varijable) dobije rečenica koja je istinita ili neistinita. Sasvim općenito: otvorena rečenica koja sadrži n različitih varijabli je n-mjesni predikat koji je istinit ili neistinit o uređenoj n-torci objekata (dakle predstavlja n-mjesnu relaciju). Tu možemo uključiti i 0-mjesne predikate, dakle rečenice bez varijabli, koje su naprosto istinite ili neistinite.

Poliadske forme omogućuju da se izraze valjane forme argumenata koji nemaju valjanu monadsku formu (koja je, vidjet ćemo, dokazivo ekvivalentna bulovskoj). Dakle, valjanost takvih argumenata možemo dokazati samo poliadski. Na primjer, takav je ovaj vrlo jednostavni argument:

\( \frac{\text{Sve elipse su krivulje.}}{\text{Tko god crta elipse crta krivulje}}\)

Premisa ima monadsku formu ∀x (Ex → Kx), tj. bulovsku formu ∀ (E → K). Konkluzija ima monadsku formu ∀x (Fx → Lx), tj. bulovsku formu ∀ (F → L). Naravno, E je elipsa, K je krivulja, F je onaj koji crta elipse, a L onaj koji crta krivulje. Dakle, monadska forma argumenta o crtačima je

\(\frac{\forall x (E x \rightarrow K x)}{\forall x (F x \rightarrow L x)}\)

Ona očito nije valjana, pa ne može objasniti očitu valjanost tog argumenta. Njegova valjanost se krije u dijadskoj formi Cyx, koju ima relacija “y crta x“. Uz njenu pomoć lako prepoznajemo ∃x (Ex ∧ Cyx) kao formu od “y crta elipse” i ∃x (Kx ∧ Cyx) kao formu od “y crta krivulje”. Dakle, poliadska forma argumenta o crtačima je:

\( \frac{\forall x (E x \rightarrow K x)}{\forall y (\exists x (E x \land C y x) \rightarrow \exists x (K x \land C y x))}\)

Poliadska će logika lako objasniti njegovu valjanost.

3. Kvantificirane forme

Da bismo formulirali logiku (poliadskih) predikata krećemo s prvim korakom izgradnje svake logike, tj. s definiranjem formi te logike. No, prije toga upozoravamo na neke važne razlike u tvorbi kvantificiranih formi u formalnim i prirodnim jezicima.

Značenje kvantifikatora ∀ je svaki, a značenje kvantifikatora ∃ je neki ili postoji, no oni gramatički ne djeluju na isti način kao u hrvatskom i drugim prirodnim jezicima. Krenemo li od otvorene rečenice sa samo jednom varijablom x, u hrvatskom bismo iz nje generirali zatvorenu rečenicu supstitucijom imena ili kvantifikatora na mjesto varijable. Na primjer:

x je dobar. ­ ­ ­ ­ Ivan je dobar. ­ ­ ­ ­ Svatko je dobar. ­ ­ ­ ­ Netko je dobar.

U logici nikada ne kvantificiramo na taj način. Varijablu x ostavljamo gdje je i bila, a kvantifikator s varijablom x prefiksiramo otvorenoj rečenici. Time pokazujemo da je kvantificirana varijabla x ili, stručnije kazano, da kvantifikator veže varijablu x. U našem primjeru:

x je dobar. ­ ­ ­ ­ Ivan je dobar. ­ ­ ­ ­ ∀x(x je dobar) ­ ­ ­ ­ ∃x(x je dobar)

Kvantifikatori “svatko” i ” netko” zapravo ni u prirodnim jezicima ne spadaju u gramatičku kategoriju imenica (usprkos površnoj sličnosti rečenica “Ivan je dobar“, “Svatko je dobar” i “Netko je dobar“). Naime, lako je naći primjere iz koji ih je jasno da oni spadaju u gramatičku kategoriju različitu od imenica. Na primjer, sljedeće rečenice očito znače isto.

Ivan je dobar ili prijetvoran. ­ ­ ­ ­ Ivan je dobar ili je Ivan prijetvoran.

S druge strane sljedeće rečenice očito ne znače isto.

Svatko je dobar ili prijetvoran. ­ ­ ­ ­ Svatko je dobar ili je svatko prijetvoran.

Prve dvije imaju ekvivalentne forme, (D ∨ P) i ⇔ Di ∨ Pi, dok druge dvije imaju neekvivalentne forme ∀x(Dx ∨ Px) ⇎ ∀x Dx ∨ ∀x Px. Razlika drugog para formi očito je u dosegu kvantifikatora. U logičkom “prefiksiranju” doseg je jasno vidljiv. U “imenskom” pristupu, kakav nalazimo u hrvatskom i drugim prirodnim jezicima, dosezi kvantifikatora nisu tako očigledni. (Često su i neodređeni; usp. rečenicu “Na toj konferenciji svi su matematičari ili logičari”.)

U skladu s Boole-Fregeovim pristupom mi ćemo kvantificirane forme definirati neovisno od njihove veze s prirodnim jezicima. Zatim ćemo definirati interpretacije kvantificiranih formi, te istinitost forme u interpretaciji (što je ključni logički pojam). Slijedit će standardne definicije implikacije, konzistentnosti, valjanosti itd. i nalaženje algoritama za njihovo testiranje. Kao i do sada, neformalne argumente izražene prirodnim jezikom smatrat ćemo valjanima ako se mogu shvatiti kao konkretne interpretacije valjanih formalnih argumenata, a tek za tu primjenu opet će biti važna veza s prirodnim jezicima. No, to su teme naših sljedećih poglavlja. Sada se vraćamo preciznoj definiciji kvantifiranih formi.

DEFINICIJA KVANTIFICIRANE FORME

Kvantificirane {-, ∧, ∨, →, ∃, ∀}-forme izgrađene su od:

• individualnih varijabli \(\small x_0, x_1, x_2, x_3, \ldots\);
• individualnih konstanti \(\small a_0, a_1, a_2, a_3, \ldots\);
• predikatskih konstanti \(\small P_0^n, P_1^n, P_2^n, P_3^n, \ldots\); za sve n ≥ 0,
• logičkih konstanti -, ∧, ∨, →, ∃, ∀.

prema pravilima (u kojima individualnu varijablu ili konstantu zovemo termom):

(i) n-mjesni predikat kojem slijedi n terma je (atomarna) forma.
(ii) Ako su F i G forme onda su (-F), (F ∧ G), (F ∨ G) i (F → G) forme.
(iii) Ako je F forma i x varijabla onda su ∃xF i ∀xF forme.

Forme koje sadrže samo 0-mjesne predikate zovemo propozicijskim formama.

Forme koje sadrže samo 1-mjesne predikate zovemo monadskim formama.

Varijable i konstante označili smo s po jednim slovom: x, a i P i indeksima: 0, 1, 2, . . . jer će to olakšati teorijska razmatranja u sljedećim poglavljima. U praksi ćemo koristiti slova x, y, z, …; a, b, c, …; P, Q, R, … (koja možemo shvatiti kao alternativne zapise x₀ = x, x₁ = y, x₂ = z, …; a₀ = a, a₁ = b, a₂ = c, …; P₀ = P, P₁ = Q, P₂ = R, … ). Svaki predikat ima gornji indeks koji mu određuje “mjesnost”. No, u praksi te indekse nećemo zapisivati jer je iz broja terma koji slijede predikatu jasno koja mu je “mjesnost”. (Ta konvencija znači da u formi Pa ∧ Pab nemamo dva primjerka predikata P, nego jednomjesni predikat P¹ i dvomjesni predikat P² koji su različiti.). Propozicijske (0-mjesne) forme označavat ćemo malim srednjim slovima abecede, p, q, r itd.

Individualne odnosno predikatske konstante zovemo konstantama, jer one u pojedinoj strukturi u kojoj interpretiramo naše forme imaju konstantne vrijednosti, koje su objekti odnosno relacije te strukture. Logičke konstante su konstante u još jačem smislu jer one imaju isto značenje (tj. iste vrijednosti) u svim strukturama.

Pravilo (iii) dopušta i tzv. praznu kvantifikaciju; stavljanje prefiksa ∃x ili ∀x pred formu F koja uopće ne sadrži varijablu x. Takve prazne kvantifikacije treba shvaćati kao da ih nema, npr. ∀xPyy ⟺ Pyy, ∃yPax ⟺ Pay, itd.

4. Monadske forme su bulovske

Kvantificirane forme kao posebni slučaj uključuju (0-mjesne) propozicijske forme. To su zapravo IF–forme čiju smo logiku već obradili. Dakle, IF–logika će očito biti dio logike kvantificiranih formi. Osim toga, svaku bulovsku formu možemo izraziti ekvivalentnom (1-mjesnom) monadskom formom. Na primjer, bulovsku formu:

∀(P ∧ Q → R) ∨ -∃(Q ∨ R → P) → -∀ ((P ∧ Q) ∨ R)

monadski izražavamo formom:

∀x(Px ∧ Qx → Rx) ∨ -∃x(Qx ∨ Rx → –Px) → -∀x ((Px ∧ –Qx) ∨ Rx).

Princip je očit i sasvim jednostavan. (Bulovske forme smo u prethodnom poglavlju definirali koristeći se samo egzistencijskim kvantifikatorom ∃, no vidjeli smo da je ∀F ekvivalentno s -∃ –F, pa u tom smislu gornja forma jest bulovska.)

S druge strane, bar na prvi pogled nije jasno da se svaka monadska forma može izraziti ekvivalentnom bulovskom formom. Na primjer, što bi mogao biti bulovski ekvivalent monadske forme ∃y∀x(Px →Qy). Ipak, može se dokazati da postoji bulovski ekvivalent svake monadske forme. To omogućuju pravila prolaza, koja vrijede za sve forme. Radi se o jednostavnim ekvivalencijama, koje nam govore kako kvantifikatori ∀ i ∃ “prolaze” kroz IF–veznike. Na primjer, ako se varijabla x ne pojavljuje u formi A onda je ∀ x (A ∧ F(x)) ⇔ A ∧ ∀xF(x) pa kažemo da “∀ prolazi kroz A ∧ bez promjene”; dok je s druge strane ∀x(F(x) → A) ⇔ ∃xF(x) → A pa kažemo da “∀ prolazi kroz F(x) → mijenjajući se u ∃“. Ta i ostala pravila prolaza posebno ističemo.

TEOREM O PROLAZU KVANTIFIKATORA KROZ IF–VEZNIKE

Ako se varijabla x ne pojavljuje u formi A onda vrijede sljedeće ekvivalencije:

­­

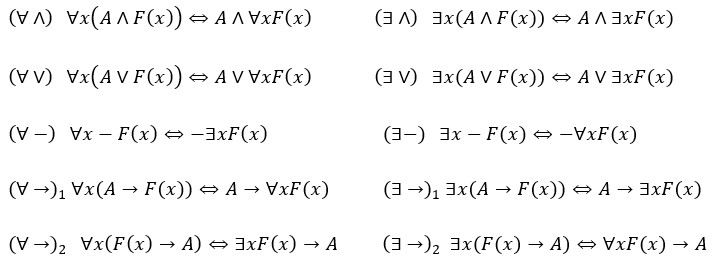
TEOREM O INTERDEFINABILNOSTI KVANTIFIKATORA

­­

Prva četiri pravila (∀∧), (∃∧), (∀∨), (∃∨) su očita. Pravila (∀−) i (∃−) također su očita i već smo ih obrazložili u okviru bulovske logike (∀ –F ⇔ -∃F , ∃ –F ⇔ -∀F). Iz njih neposredno slijedi interdefinabilnost kvantifikatora. Pravila (∀ →)₁ i (∃ →)₁ svode se na pravila (∀ ∨) i (∃ ∨). Na primjer,

­­

Pravila (∀ →)₂ i (∃ →)₂ iznenađuju no i ona slijede iz (∀ -),(∃ -),(∀ ∨) i (∃ ∨). Npr.

­­

Razliku između ∃x(F(x) → A) i ∃xF(x) → A riječima možemo izraziti na sljedeći način:

Neki x je takav da,ako F(x) onda A. ­ ­ ­ ­ Ako je neki x takav da F(x),onda A.

Razliku između ∀x(F(x) → A) i ∀xF(x) → A riječima izražavamo ovako:

Svaki x je takav da,ako F(x) onda A. ­ ­ ­ ­ Ako je svaki x takav da F(x),onda A.

Da bismo bolje razumjeli ove razlike, interpretirajmo F(x) kao “student x će položiti taj ispit”, a A kao “profesor će biti iznenađen”. Tako interpretirana, forma ∀x(F(x) → A) izriče da će svaki student, pa i najbolji, iznenaditi profesora ako položi ispit. Drugim riječima, profesor ne očekuje nijedan prolaz. Forma (∀xF(x)) → A ne odiše tolikim pesimizmom, ona izriče da će profesor biti iznenađen ako svi studenti polože taj ispit. Razlika je očita.

U prirodnim jezicima ta se razlika najčešće ne iskazuje različitim dosegom kvantifikatora nego različitim riječima kojima se izriče kvantifikacija. Na primjer, univerzalna kvantifikacija u hrvatskom se može izraziti riječima “svaki” i “bilo koji”. Na primjer, rečenice:

Svaki će student položiti taj ispit. ­ ­ ­ ­ Bilo koji student će položiti taj ispit.

znače isto. Njihova forma je ∀xF(x). Međutim rečenice:

Ako svaki student položi taj ispit profesor će biti iznenađen.

Ako bilo koji student položi taj ispit profesor će biti iznenađen.

očito ne znače isto. Njihove su forme (∀xF(x)) → A i ∀x(F(x) → A). Čini se da “bilo koji” u hrvatskom jeziku ima veći doseg od “svaki”. Za drugu rečenicu čak možemo reći da je sinonimna sa:

Ako neki student položi taj ispit profesor će biti iznenađen.

Sada možemo pomisliti da su “bilo koji” i “neki” sinonimi, tj. da “bilo koji” u ovom slučaju nije univerzalni kvantifikator, nego partikularni. No, sinonimnost zadnje dvije rečenice bolje je objasniti kao ekvivalenciju formi ∀x(F(x) → A) i (∃xF(x)) → A. Dakle, “bilo koji” je i u ovom slučaju univerzalni kvantifikator kao i “svaki”, samo je većega dosega. To ipak nije neko opće pravilo. Na primjer, čini se da u rečenicama

Svaki student je položio logiku ili matematiku.

Bilo koji student je položio logiku ili matematiku.

i “svaki” i “bilo koji” imaju veći doseg, tj. da obje rečenice imaju formu ∀x(Lx ∨ Mx). U slučaju negacije:

Ja ne znam otpjevati svaku pjesmu. ­ ­ ­ ­ Ja ne znam otpjevati bilo koju pjesmu.

“svaki” sigurno ima manji opseg, tj. forma prve rečenice sigurno je -∀xOx, dok je druga ambivalentna i zapravo neuobičajena. Uobičajeno bi bilo reći:

Ja ne znam otpjevati nikoju pjesmu.

i ta rečenica sigurno ima formu ∀x(-Ox). U ovom slučaju dodatna negacija (“nikoju”) nedvosmisleno povećava doseg univerzalnog kvantifikatora, i to je njezina funkcija u hrvatskom i ostalim slavenskim jezicima. Dakle, nije riječ o “nelogičnim Slavenima” koji ne razumiju da je dvostruka negacija afirmacija, nego o “logički sofisticiranim Slavenima” koji pojačanu (dvostruku) negaciju koriste kao jasnu naznaku povećanog dosega kvantifikatora. No, vratimo se našim formalno logičkim temama.

Pravila prolaza možemo koristiti u oba smjera; tako da proširimo doseg kvantifikatora ili tako da ga suzimo. Prvi smjer izvlači kvantifikatore iz forme dok ih drugi u nju uvlači. Pri tome se koriste sljedeće očite ekvivalencije (uz njih naglašavamo i one koje očito ne vrijede).

TEOREM O DISTRIBUCIJI KVANTIFIKATORA KROZ ∧ I ∨

­­

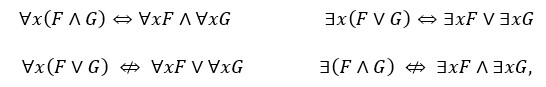
Evo prvo jednog poliadskog primjera koji ilustrira kao se svaka kvantificirana forma može prevesti u ekvivalentnu preneksnu formu. To je forma u kojoj su svi kvantifikatori izvučeni na početak forme:

­­

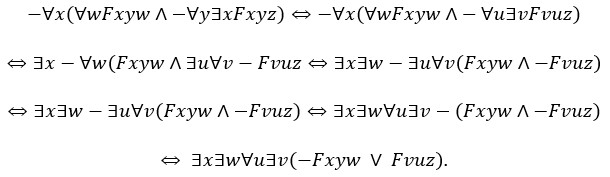
­Uvlačenje kvantifikaora posebno je zanimljivo u slučaju monadskih formi, jer njime dokazujemo ekvivalentnost bulovskih i monadskih formi pa time i bulovske i monadske logike. Ilustriramo to primjerom uvlačenja kvantifikatora u sljedeću monadsku formu:

∀x[∃y(Fx ↔ Gy) ∨ ∃yFy] ∧ ∀x[Fx ∨ Gx]

Najprije uvučemo početni ∀x primjenom pravila prolaza:

[∀x∃y(Fx ↔ Gy) ∨ ∃yFy] ∧ ∀x[Fx ∨ Gx]

(Fx ↔ Gy) zapišemo u ekvivalentnoj alternacijskoj formi ((Fx ∧ Gy) ∨ (-Fx ∧ –Gy) pa kvantifikator ∃y distribuiramo kroz tu alternaciju:

[∀x(∃y(Fx ∧ Gy) ∨ ∃y(−Fx ∧ −Gy)) ∨ ∃yFy] ∧ ∀x[Fx ∨ Gx]

Zatim pomoću pravila prolaza uvlačimo prva dva ∃y:

[∀x((Fx ∧ ∃yGy) ∨ (−Fx ∧ ∃y−Gy)) ∨ ∃yFy] ∧ ∀x[Fx ∨ Gx]

Sada (Fx ∧ ∃yGy) ∨ (−Fx ∧ ∃y−Gy) zapišemo u ekvivalentnoj konjunkcijskoj formi (Fx ∨ ∃y−Gy) ∧ (∃yGy ∨ −Fx) ∧ (∃yGy ∨ ∃y−Gy) pa kvantifikator ∀x distribuiramo kroz tu konjunkciju:

[∀x(Fx ∨ ∃y−Gy) ∧ ∀x(∃yGy ∨ −Fx) ∧ ∀x(∃yGy ∨ ∃y−Gy) ∨ ∃yFy] ∧ ∀x[Fx ∨ Gx]

Uz još dva uvlačenja kvantifikatora ∀x dolazimo do ekvivalentne forme u kojoj kvantifikatori djeluju samo na atomarne forme:

[(∀xFx ∨ ∃y−Gy) ∧ (∃yGy ∨ ∀x−Fx) ∧ (∃yGy ∨ ∃y−Gy) ∨ ∃yFy] ∧ ∀x[Fx ∨ Gx]

Nju je sada trivijalno prevesti u bulovsku formu:

\( [(\forall F \lor \exists \overline{G})(\exists G \lor \forall \overline{F})(\exists G \lor \exists \overline{G}) \lor \exists \overline{F}] \land \forall [F \lor G]\)

Prevođenje monadske kvantifikacije u bulovsku može se provesti i na drugačiji način. Monadska forma Qx(…A…), gdje je Q može biti ∀ ili ∃, a u kojoj forma A ne sadrži varijablu x, ekvivalentna je formi \(\small (A \land Qx(\ldots \top \ldots)) \lor (\overline{A} \land Qx(\ldots \bot \ldots))\). U toj formi forma A više nije u dosegu kvantifikatora Q. Postupak nastavljamo dok ne eliminiramo sve takve „nečistoće“. Na kraju dolazimo do ekvivalentne forme u kojoj kvantifikatori Qx u svojem dosegu nemaju varijable različite od x i to su očito bulovske forme. Iako je opis ovog postupka jednostavniji njegova je primjena složenija (što se čitatelj može i sam uvjeriti tako da ga primijeni na gornju formu).

Dakle, izražajna snaga monadske kvantifikacije samo je naizgled veća od bulovske. Njezine „nečiste“ uklopljene kvantifikacije nepotrebne su komplikacije koja ne donosi ništa novo (uz malu ogradu da monadske forme mogu biti otvorene, dok su bulovske po definiciji zatvorene).

Ovim dokazom ekvivalentnosti bulovskih i monadskih formi riješili smo pitanje odlučivosti monadske logike. Je li monadska forma valjana ili konzistentna, implicira li jedna drugu ili jesu li ekvivalentne, odlučujemo tako da ih prevedemo u bulovske ekvivalente i dođemo do odluke kako je to objašnjeno u poglavlju o bulovskoj logici pojmova.

Već smo pokazali da se svaka monadska forma može prevesti u preneksni oblik. No, vrijedi i više od toga. Moguće ju je prevesti u preneksni oblik s bilo kojim redoslijedom kvantifikatora. Naime, preneksnu formu možemo prevesti u ekvivalentni bulovski oblik koji nema kvantificiranih kvantifikacija. Iz njega kvantifikatore možemo izvlačiti u kojem god želimo redoslijedu i tako doći do ekvivalentne preneksne forme s kojim god redoslijedom kvantifikatora. To monadske forme bitno razlikuje od poliadskih, jer ∀x∃yPxy ⇎ ∃x∀yPxy (npr. za x, y ∈ \(\small \mathbb{N}\) očito ∀x∃yx > y ⇎ ∃x∀yx > y).

Leibniz je vjerovao da se relacije mogu reducirati na svojstva (tj. da se poliadske forme mogu uvijek izraziti monadskim formama), ali to nije uspijevao dokazati. Sada je jasno i zašto. Zato što to nije moguće.