Zasto je arapskim brojevima trebalo vise od pola milenija da zamijene rimske?

Stephen Chrisomalis u knjizi Reckonings istražuje zamjenu rimskih brojeva arapskima kao složen proces koji je trajao više od pet stoljeća, osporavajući uvjerenje da su arapski brojevi prihvaćeni isključivo zbog efikasnosti, piše Željko Ivanković. Koristi se uvidima iz lingvistike, kognitivne znanosti i povijesti kako bi objasnio okolnosti promjene notacije brojeva, pri čemu otvara put potpunijem razumijevanju povijesti i značenja matematičkih koncepata poput - nule.

Naslovna fotografija: Detalj s knjige Reckonings: Numerals, Cognition and History (MIT Press, 2020).

I

Otkad se, najkasnije potkraj desetog stoljeća pobliže upoznao s arapskim brojevima[i], zapadu je Europe trebalo više od pola milenija da njima dominantno zamijeni rimske, kojima se uglavnom služio dvije tisuće godina. Iako ih je već 1202. godine u ‘Knjizi o računanju’ (Liber Abaci) preporučivao veliki i utjecajni matematičar iz Pize Leonardo Fibonacci, zamjetno prihvaćanje arapskih brojeva započelo tek s Gutenbergom i zamahom tiskanja prema kraju 15. stoljeća, a konačnu su dominaciju nad rimskim brojevima dostigli tek u 17 stoljeću, tvrdi lingvistički antropolog Stephen Chrisomalis u knjizi Reckonings: Numerals, Cognition and History (MIT Press, 2020).

Ta tvrdnja relativizira ‘tradicionalni narativ’ prema kojem su arapski brojevi prihvaćeni isključivo kao lakši za upotrebu (efikasniji), a kojem se – uočava i ističe i sam Chrisomalis – priklanjaju jednako (‘prosječni’) korisnici i stručnjaci za numeraciju. Kad bi god nekog pitao što misli zašto su rimski brojevi zamijenjeni arapskima uobičajena bi reakcija bila: „Jeste li ikad pokušali tim (rimskim) brojevima množiti?“ Naravno, množenje je bilo dobro poznato korisnicima rimskih brojeva, kao uostalom i dijeljenje, a u doba samog Rimskog carstva aritmetika je već bila složena. Zanimljivo, za operacije s razlomcima koristili su se duodecimalnim sustavom, piše Chrisomalis. Ispada da je napuštanje jednog sustava zapisivanja brojeva i zamjena drugim kudikamo složenija nego što se na prvu pretpostavlja. Autor knjige nastoji prodrijeti u strukturu i sve činitelje tog procesa, a u završnom poglavlju čak raspravlja (ne)mogućnost zamijene arapskih brojeva nekim od već konstruiranih ‘efikasnijih’ sustava.

­­

U ranijoj je knjizi Chrisomalis sistematizirao otprilike 100 različitih sustava zapisivanja brojeva poznatih u povijesti.

Deset godina prije knjige o računanju Chrisomalis je objavio i knjigu Numerical Notations: A Comparative History (Cambridge University Press, 2010), koja je rezultat njegova doktorata na Sveučilištu McGill. U njoj je prikazao, analizirao i na svoj način sistematizirao otprilike 100 različitih sustava zapisivanja brojeva poznatih u povijesti, a od kojih su neki (rijetki) i danas u upotrebi, iako svijetom, očigledno, dominiraju arapski, odnosno indo-arapski brojevi, koje sam naziva zapadnima. Već tad predloženo mu je da uz tu specijalističku knjigu napiše jednu za ‘širu publiku’.

II

Reckonings naravno nije ‘popularizacija’, nego knjiga šire ambicije. Autor u njoj ne istražuje samo jednu nego povijesne promjene općenito (filozofi bi rekli – po sebi, kao takve). U tu se svrhu zamjena rimskih brojeva arapskima čini sjajnim izborom. Charles Burnett piše da je riječ o najvažnijoj promjeni u povijesti predmoderne matematike[ii]. Sama je matematika respekt uživala već od Antike, a svojom izdvojenom i najvišom pozicijom natkriljuje i suvremenu znanost. U modernoj su filozofiji povijesne promjene jedno od dominantnih pitanja, sve od Lockea koji piše o skoku iz prirodnog i civilizirani svijet, do Hegela i kasnije, u devetnaestom i u dvadesetom stoljeću. Neki ih prepoznaju i istražuju u ekonomskim promjenama, drugi u socijalnim, kulturnim (koje uključuju i znanost), izrazito se često poistovjećuju s političkim promjenama, odnosno ‘napretkom u svijesti o slobodi’ koja je također egzemplarni novovjeki koncept. No za Novi je vijek karakteristično, čak konstitutivno da se povijest općenito gleda kao progres. Ostavimo li po strani radi li se uopće o napretku, za koga i kako se identificira, ostaje pitanje jesu li promjene (na bolje) posljedica uvođenja demokracije, cilj ili tek ishod znanosti i razvoja tehnologije.

Zapisivanje brojeva je svojevrsna tehnika (tehnologija). Veliki dio knjige Chrisomalis posvećuje opovrgavanju teze da su arapski brojevi prihvaćeni jer su efikasniji za manipulaciju nego rimski. Time se ponajprije suprotstavlja zaključcima (a) da je veća efikasnost, kako god mjerena, primarna mjera boljitka te (b) da je težnja prema efikasnosti, barem u slučaju zapisivanja brojeva, uzrok promjena. Navodi nekolicinu efikasnijih tehnologija koje nisu prihvaćene, među njima i vrlo česti primjer QWERTZU-rasporeda slova na alfabetskoj tipkovnici, koji je opstao iako su predloženi novi koji bi omogućili brže i tipkanje s manje pogrešaka, no njihovo bi usvajanje zahtijevalo promjenu navika i zaokret u industriji[iii]. Malo nade za usvajanje u doglednom razdoblju imaju i sustavi bilježenja brojeva koji su ‘efikasniji’ nego arapski brojevi. Ali, ako su arapski brojevi čak i bili efikasniji (lakši) nego rimski za čitanje i računanje, a što Chrisomalis pokušava pokazati da nije lako dokazivo, svejedno ne mora biti da je baš to bio razlog što su nakon višestoljetne ‘muke’ prihvaćeni. Kad su pak napokon usvojeni svijetom su se raširili zahvaljujući političko-ekonomskoj dominaciji Zapada, tvrdi.

S indijskim su se brojevima i Arapi upoznali u sedmom stoljeću, a još su se dugo koristili i drugim notacijama. Ni Indija nije primjenjivala samo jedan način zapisivanja brojeva. Zašto su na Zapadu na kraju zadominirali i osvojili svijet?

Neproduktivno je Chrisomalisa, zbog teze o ‘nametanju’ zapadnih brojeva cijelom svijetu, svesti na još jednog kulturnog ‘dekolonizatora’ i na taj način zanemariti doprinos njegove knjige koja je dobrim dijelom jedan pregled uvida mnoštva istraživača. Ostaje činjenica da su prošla stoljeća prije nego su prihvaćeni na Zapadu, da su se s njima i Arapi upoznali u sedmom stoljeću[iv] a još su se dugo koristili i drugim načinima zapisivanja brojeva, o čemu sve autor podastire izvore, kao i činjenica da ni Indija u kojoj su (zajedno s nulom i mjesnom vrijednošću broja kreirani) nije na svom teritoriju i u svom susjedstvu primjenjivala samo taj način zapisivanja brojeva. Pitanje je, dakle – zašto? Zašto je trajalo toliko dugo i zašto se napokon dogodilo?

III

Prvo se poglavlje Chrisomalisove knjige bavi limitom brojanja i računanja napamet (subitizacija), drugo govori o sklonosti velikim brojevima i zaokruživanju. Treće i četvrto poglavlje knjige eksplicite su posvećeni arapskim i rimskim brojevima. U petom je tema pismo od 85 znakova koje je za svoj jezik smislio Sequoyah, američki domorodac, a službeno ga je prihvatio Nacionalni savjet Cherokee Indijanaca i još se koristi. Chrisomalis zapravo raspravlja zašto je Nacionalni savjet odbio sustav zapisivanja brojeva koji je, kao prikladan Cherokeeima Sequoyah također izumio, nego je prihvatio arapsku notaciju: brojevi su, komunikacijski i kognitivno, ipak drugo nego slova. Šesto je poglavlje opet ‘kognitivno’ kao i prva dva, odnosno lingvističko: govori o modalitetima korištenja različitih načina zapisivanja brojeva, tj. zašto i danas brojeve neki put pišemo slovima drugi put znamenkama i sl. Posljednje je poglavlje spekulativno, raspravlja o onome što nam je ‘čudno’, dakle i o navikama, koje su ‘čovjekova druga priroda’ i što smatramo nepromjenjivim, što univerzalnim a što partikularnim.

Nacionalni savjet Cherokee Indijanaca prihvatio je pismo koje je, prilagodjeno njihovom jeziku, izumio Sequoyah, ali nije prihvatio način zapisivanja brojeva, vjerojatno zato što su smatrali da im zajednički način zapisivanja brojeva omogućava lakše sporazumijevanje s drugima. (Ilistracija iz Chrisomalisove knjige.)

Prema vlastitim riječima Chrisomalis je lingvistički antropolog. Ambiciozan je objasniti povijesne promjene ‘kao takve’, ali ne na razini pojma, kao filozofski čistunci. U knjizi se koristi uvidima kognitivne znanosti, psihologije, sociologijom, etnologijom, kulturologijom, historijom, sve disciplinama koje su, kao i lingvistika, sastavnice antropologije. Ustvari se, gledajući iz toliko očišta, nastoji što više približiti stvarnosti: rastaviti sat, vidjeti kako radi i iz toga pokušati shvatiti protok vremena. Čitatelju koji, poput mene, te discipline ne poznaje dovoljno, neki put nije jasno kamo autor vodi, a na kraju izmiče i strukturirana cjelina. Svejedno, moguće je rekonstruirati kako su, u Chrisomalisovoj interpretaciji,  arapski brojevi zamijenili rimske, a također steći mnoge druge vrijedne uvide.

IV

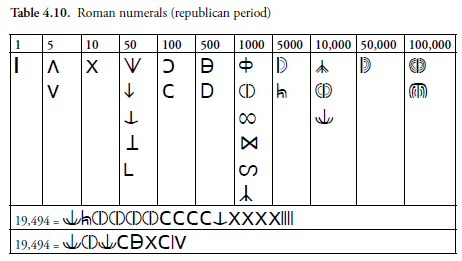
U dvije tisuće godina koliko je dominirala današnjim zapadnim svijetom, rimska je notacija brojeva sama prošla niz izmjena i usavršavanja, već prema potrebi. Iz vremena kad su brojevi bili puki zapis brojanja i danas se na nekim satovima može naći broj 4 zapisan kao IIII, a ne IV. Kad su u Srednjem vijeku prepisivani stari spisi, pisari su znali pomisliti da je XXXX greška, da to ne znači XL, pa su prepisivali kao XXX. Reformi zapisivanja brojeva suprotstavlja se dakle i inercija, komunikacija s prošlošću, napominje Chrisomalis. Sljedećim usavršavanjem tisuću puta veći broj dobio bi iznad sebe crtu, pa je 10.000 bilo zapisivano kao a sto tisuća puta veći broj bi bio zaokružen s još dvije uspravne crte pa je dobio – П. Zacijelo najzanimljiviji pokušaj usavršavanja rimskih brojeva izveo je početkom 12. stoljeća Ocreatus, koji im je dodao nulu na prazno decimalno mjesto pa je broj 408 u njegovoj notaciji pisan kao IV.0.VIII. To je, međutim, ostao izolirani akademski eksperiment ali vrlo koristan za razumijevanje načina zapisivanja brojeva u drugim kulturama (Kina) i – nule, ‘himere’ među brojevima.

Rimski su brojevi i dvije tisuća godina upotrebe sami prošli niz usavršavanja. Iz knjige Numerical Notation.

Glavni je argument zagovornika arapskih brojeva da su oni lakši (efikasniji) u izvedbi računskih operacija. Glavni je Chrisomalisov protuargument trostruk: a) notacija brojeva ne služi računanju nego prikazu veličina; b) jesu li arapski brojevi zaista efikasniji?; c) ako su i efikasniji, to nije bio to nije bio dovoljan razlog da se rimski brojevi generalno zamijene arapskima. U vrijeme korištenja rimskim brojevima računalo se na površinama, odnosno pločama za računanje, te također na računaljkama (abacus/abakus). Chrisomalis navodi niz primjera u kojima se abacus pokazao efikasnijim u računanju ne samo od onih koji su računali arapskim brojevima (množili, dijelili, vadili korijen), nego je u Japanu 1946. održano natjecanje u kojem je korisnik abacusa pobijedio Amerikanca koji se služio tada najrazvijenijim strojem za računanje. Nakon računanja na abacusu rezultat bi se upisivao rimskim brojevima (ili u slučaju Dalekog Istoka njihovim notacijama). Chrisomalis ne spominje, no i danas se za računske operacije sve više koriste računala, samo elektronska, a sve se manje računa na papiru. Notacija brojeva dakle ne služi prvenstveno računanju nego bilježenju veličina (rezultata). To je glavni zaključak lingvističkog antropologa Chrisomalisa o prirodi notacije brojeva. No taj zaključak samo opovrgava da je računanje bilo glavni razlog zamjene rimskih brojeva arapskim, ali još ne objašnjava zašto se zamjena ipak dogodila.

Abacus s rimskim brojevima, ilustracija iz Chrisomalisove knjige Reckonings.

U raspravi između tzv abacista i algorista[v], koja – naglašava autor knjige Reckonings – i nije bila isključivo polemičko suprotstavljanje nego isticanje prednosti i nedostataka jednog i drugog načina računanja, jedan je argument zagovornika arapskih brojeva (algorista) bila transparentnost računa. Međutim, metoda računanja na abacusu vrlo je jasna, osobito onima koji se u nju malo upute. Ustvari je izvedba osnovnih računskih operacija slična kao kod primjene algoritma za izračun, osniva se na istim načelima, a oni koji su spretni u abacusu znali su i ‘u glavi’ izvoditi operacije s velikim brojevima zamišljajući da ih izvode na abacusu. Analizom manuskripta Barnett svjedoči kako su pravila računanja i na abacusu i na papiru u početku vrlo zamršeno formulirana, dok se nisu praksom iskristalizirala. Chrisomalis i time više dovodi u pitanje da je efikasnost bila glavni i dovoljan razlog zamjene rimskih brojeva, nego da su arapski zaista efikasniji.

Promjenu se znalo objašnjavati većom prikladnošću arapske notacije u komercijalnoj djelatnosti koja se krajem Srednjeg vijeka počela snažno razvijati. U to je doba započeo je i razvoj dvojnog knjigovodstva. Dakako, ono je bilo primjenjivano i s rimskim brojevima, a Firenca je čak u jednom trenutku zabranila u komercijalnim poslovima upotrebu arapskih brojeva, zbog toga što ih je, kao manje poznate, bilo lakše falsificirati, na primjer prepravljanjem cifre 6 u 8. Sveučilište iz Padove zahtijevalo je da cijene ne budu istaknute u arapskim nego u rimskim brojevima (non per cifras sed per litera clara).

Firenca je čak u jednom trenutku zabranila u komercijalnim poslovima upotrebu arapskih brojeva, zbog toga što ih je, kao manje poznate, bilo lakše falsificirati

Kako su onda rimski brojevi ipak zamijenjeni arapskim? Chrisomalis identificira više silnica koje su se na kraju ipak spojile. Tako se povijest inače odvija, ne da se reducirati na jedan faktor. Arapski su se brojevi koristili u matematičkim spisima u komunikacijske svrhe, za demonstraciju ispravnosti izračuna. To su naravno bili i edukacijski materijali. Prvo su se s arapskim brojevima familijarizirali studenti matematike a onda i drugi koje su oni poučavali matematici (aritmetici).

Naravno, ključni je moment bio tiskarski stroj. Samim je tiskarima trebalo vremena da usvoje arapske brojeve. Nisu bili tipografski oblikovani, pogotovu ne jasno. Na početku su primjenjivani tek za obilježavanje araka, a zatim i poglavlja, odnosno paragrafa, za ono za što se danas često koriste rimski brojevi. No s vremenom su prvo u matematičkim knjigama ipak otiskivani arapski brojevi, a zatim i u komercijalne svrhe. Trgovci nisu nosili sobom abacus, a ni ploča na kojoj bi ga crtali nije bila praktična koliko zbrajanje cijena na papiru. Svi su ti faktori: komunikacija, demonstracija izračuna, edukacija, generacijska promjena, tiskarski stroj, trgovina – bili od utjecaja.

V

Nekolicina je istraživača rimske brojeve predstavila kao izraz kognitivne zaostalosti, a njihovu zamjenu arapskima kao misaoni skok. Neki su u zapadnoj notaciji čak vidjeli ‘kraj povijesti’ u zapisivanju brojeva. Ti su zaključci glavni cilj Chrisomalisove analize i opovrgavanja prvoloptaških pretpostavki. No kad je ušao u materiju na vidjelo je iznio obilje materijala o brojevima te socijalnim, komercijalnim, lingvističkim, kognitivnim, političkim i drugim aspektima prakse računanja.

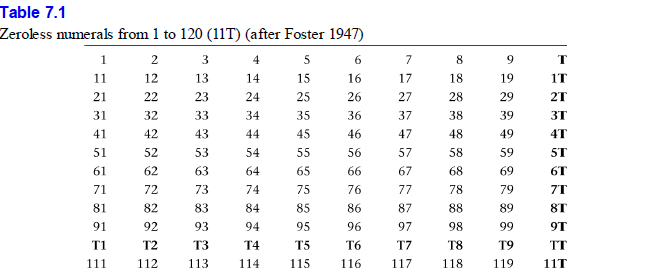
Posljednje je poglavlje svojevrsni misaoni eksperiment, još jedna rasprava o karakteristikama kognicije, uvriježenih mišljenja koje se doživljava kao da su urođena, prirodna, o tome što je obično a što neobično, a posredno i o komunikaciji i politici. U njemu je možda najzanimljiviji primjer sustava zapisivanja brojeva koji je 1947. godine smislio matematičar amater James E. Foster u kojem nema nule za označavanje mjesne vrijednosti, a ipak njime može sve izvesti što i arapskim brojevima[vi]. Deset se bilježi kao T, dvadeset kao 1T, stotinu kao 9T, a stotinu i jedan kao T1. Dakako, nama je kontraintuitivno da kod pisanja broja dvadeset nema broja dva. Ali u zapisivanju brojeva u prvi je mah puno toga kontraintuitivno.

Fosterov sustav zapisivanja brojeva u kojem nema nule.

Nuli je trebalo dugo da dobije današnju funkciju u pisanju brojeva. Kinezi su imali decimalni sustav s posebnim znakovima za desetice, stotice itd. Ako bi željeli napisati broj 208 upisali bi  dva puta stotica, ostavili prazno mjesto i onda zapisali osam puta jedinica. Poput Ocreatusa, koji je u prazno mjesto upisivao nulu, i Kinezi su je s vremenom usvojili od susjeda, Indijaca. Navodno prvi tragovi datiraju već u sedmo stoljeće, kao i kod Arapa. Zato postoji spor o tome kad su zapravo uveli decimalni sustav i mjesnu vrijednost u zapisivanju brojeva – tek kad su usvojili nulu kao znak ili već dok su ostavljali prazno decimalno mjesto. Prema filozofkinji Helen de Cruz, na koju se autor poziva, usvajanje nekih numeričkih pojmova, kao što je nula, ne ide glatko jer su izrazito kontraintuitivni, no kad se jednom usvoje njihova neobičnost postaje privlačna.

Knjige poput Chrisomalisove višestruko su važne. Prvo, otvaraju put potpunijem razjašnjavanju značenja/važnosti matematičkih koncepata kao što su decimalni sustav, mjesna vrijednost broja, nula itd., jer se razmatraju i iz drugih perspektiva a ne samo iz matematičke[vii]. Matematiku se potpunije razumije ako je se demonopolizira, ako je se ne prepusti samo matematičarima. Nula je, na primjer, višeznačan pojam: označava simbol, također prazno mjesto u pisanju brojeva, a napokon je i broj čije je kasnije korištenje u matematici išlo uz svojevrsne ‘kompromise’[viii]. Razlikuje se nula u pisanju brojeva i nula kao broj kojim se po posebnim pravilima dijeli, množi, potencira itd.

Zatim je pokazano da za prihvaćanje arapskih brojeva ‘popularizacija znanosti’ i usvajanje principa ‘slušajmo eksperte’ nisu dovoljni. Ta su dva pristupa ograničeni povijesno i kulturološki. Fibonaccijevi razlozi za prihvaćanja arapske notacije nisu bili dovoljni (a možda ni smisleni) dok se nisu stekli drugi preduvjeti. Nisu ljudi Srednjeg vijeka bili glupi. Napokon, povijest se ne da reducirati na velike principe (politički progres, efikasnost) koji su najčešće još i ideologizirane generalizacije. Kroz maglu koja se na povijest kontinuirano spušta Chrisomalis nastoji prodrijeti do razumijevanja kako su stvari zaista funkcionirale.

• Bilješke

[i] Arapsku su numeraciju u današnju Europu donijeli Mauri invazijom Iberskog poluotoka u prvoj polovici 8. stoljeća, ali je tek Gerbert, koji je na samom kraju 10. stoljeća postao papa Silvester II, najraniji učenjak za kojeg je pouzdano ustanovljeno da se služio arapskim brojevima (Barbara E. Reynolds, 1993: The Algorists vs. the Abacists: An Ancient Controversy on the Use of Calculators, The College Mathematics Journal)

[ii] Charles Burnett, 2002: Learning Indian Arithmetic in the Early Thirteenth Century, Boletın de la Asociacion Matematica Venezolana, 2002

[iii] U raspravi o QWERTZU-rasporedu slova na tipkovnici dovedeno je u pitanje jesu li alternativni rasporedi zaista efikasniji, no poanta je da ako i nisu to nije bila glavna prepreka zamjeni inicijalnog rasporeda slova.

[iv] Podatci o ‘prvim’ pojavama numeričkih sustava ili su neprecizni ili različiti kod različitih autora. Tako je prema Burnettu islamski svijet upoznao indijske brojeve u devetom stoljeću kad je njihovo korištenje opisao al-Khwarizmi. Chrisomalis međutim piše da je sirijski učenjak Severus Sebokht bio jedan od prvih koji je 662 godine opisao indijski sustav brojeva. Na slične se ‘nesporazume’ nailazi i u mnogim drugim člancima i poglavljima knjiga o temama koje se ovdje raspravljaju.

[v] Kao i o svemu drugome literature o raspravi abacista i algorista je brojna. Puno se reference može naći i u Chrisomalisovoj knjizi. Uz Reynolds i Burnetta (prve dvije bilješke) ovdje još dodajem:

Williard E. Stone, 1972: Abacists versus Algorists, Journal of Accounting Research

[vi] James E. Foster, 1947: A Number System without a Zero-Symbol. Mathematics Magazine

[vii] Chrisomalis se naravno ne bavi realnim i imaginarnim brojevima, no ti i drugi pojmovi također se razmatraju u drugim disciplinama, na primjer u historiji i filozofiji, a ne samo u matematici, što omogućava njihovo potpunije razumijevanje.

[viii] Carl B. Boyer, 1944: Zero: The Symbol, the Concept, the Number, National Mathematics Magazine; Rick Blake, Charles Verhille, 1985: The Story of 0, For the Learning of Mathematics

• Video u kojem Chrisomalis predstavlja svoju knjigu.