Zašto većina eksperimentalnih istraživanja u ‘soft’ znanostima nije istinita

Ako je vjerojatnost lažnog pozitivnog rezultata manja od pet posto (p-vrijednost) većina istraživača smatra hipotezu prihvatljivom. Ključni je problem te (Fisherove) metode što evaluira samo jednu, tzv. nul-hipotezu, uzimajući u obzir sve rezultate eksperimenta koji su se mogli desiti, piše Zvonimir Šikić. A nas zapravo zanima evaluacija svih mogućih hipoteza na temelju rezultata jednog eksperimenta

Većina eksperimentalnih istraživanja u soft znanostima svoju potvrdu vidi u p-vrijednosti manjoj od 5%. To je vjerojatnost dobivenog ishoda eksperimenta pod uvjetom da je hipoteza istraživanja netočna (vjerojatnost tzv. lažno pozitivnog rezultata). Zvuči razumno. Naime, ako bi  hipoteza bila netočna desilo bi se nešto što je veoma malo vjerojatno, pa slijedi da je hipoteza vrlo vjerojatno točna (mnogi čak misle da je hipoteza tada 95% točna). Uostalom, tu je metodu predložio R. Fisher, otac moderne statistike.

Ipak, pokušaji repliciranja eksperimentalnih rezultata s p-vrijednostima manjim od 5%, koji su objavljeni u vodećim psihološkim časopisima, utvrdili su da ih je uspješno replicirano manje od polovice (Science 28, 2015.). Sve je rađeno vrlo pažljivo i uz pomoć izvornih autora. Slični neuspjesi repliciranja utvrđeni su i u drugim područjima. Pokušaji repliciranja ‘krucijalnih’ rezultata u istraživanju raka, pokazali su da ih je uspješno replicirano 11% (Nature 483, 2012.). O tome je još 2005. pisao J. Ioannidis u radu pod naslovom “Why Most Published Research Findings are False” (PLoS Medicine 2/8):

Istraživanja nisu najprikladnije predstavljena i sažeta p-vrijednostima, ali, nažalost, rašireno je mišljenje da bi medicinski istraživački članci trebali biti interpretirani samo na temelju p-vrijednosti.

O čemu se tu radi? Prije svega uočite da 5% šanse za lažni rezultat znači da će se on u prosjeku pojaviti jednom u 20 eksperimenata. Istraživači mogu eksperiment ponavljati dok ne dođu do željenog rezultata (u prosjeku će trebati 20 pokušaja, ali katkada će biti dovoljno svega par). Ako i isključimo svjesnu prevaru, istraživači neuspjele pokušaje mogu odbaciti nesvjesno, kao neuspjele zbog raznih tehničkih razloga. Osim toga, ako ne dođu do p-potvrde svoje hipoteze istraživači rezultat neće objaviti, ali prosječno će svaki 20-ti slučajno doći do p-potvrde i svoj će rezultat objaviti. Na kraju vidimo samo ono što je objavljeno. Moguće je da istraživač nakon eksperimenta svoju hipotezu zamjeni novom hipotezom za koju je p < 5%. To je matematički nekorektno, iako mnogi istraživači to ne znaju – katkada je neznanje put do uspjeha, što objašnjava čestu pojavu da ljudi odbijaju da im se nešto objasni. Aplikaciju za razne vrste ovakvih p-hackinga možete naći na blogu N. Silvera http://fivethirtyeight.com/features/science-isnt-broken/#part2.

Na sreću, danas postoji jak pokret protiv slijepe upotrebe p-vrijednosti. Sve više istraživača razumije da ne smiju zanemarivati neuspjele eksperimente, da je važno prijaviti i negativne rezultate, da ne smiju usklađivati svoje hipoteze s ishodima eksperimenta itd. Još je važnije da to razumije sve veći broj editora znanstvenih časopisa i da u skladu s tim odlučuju što će objaviti. Mnogi časopisi više ne prihvaćaju malu p-vrijednost kao argument za valjanost istraživanja (npr. Basic and Applied Social Psychology 37/1, 2015.). Respektabilne znanstvene asocijacije poput American Statistical Association daju službene izjave o nekorektnom korištenju p-vrijednosti (The American Statistician 70/1, 2016.). Medicinski časopisi objavljuju članke poput „A Dirty Dozen: Twelve P-Value Misconceptions“ (Seminars in Hematology 45/3, 2008.). I tako dalje.

Ono što je trebalo biti tek indicija da je istraživanje ‘obećavajuće’ pretvorilo se u zaključak da je ‘dokazano’. Ronald Fisher (Wikipedia)

No, što je s Fisherovim argumentom iz prvog pasusa? On je naprosto netočan. Fisher zapravo nije ni tvrdio da je točan, nego ga je samo naveo kao indiciju da je istraživanje obećavajuće. S vremenom se „obećavajuće“ pretvorilo u „dokazano“. Zašto je do toga došlo složeno je pitanje povijesti odnosa frekvencijskog i bajesovskog razumijevanja vjerojatnosti, o čemu više uskoro. No, odmah možemo reći što slijedi iz Bayesove formule:

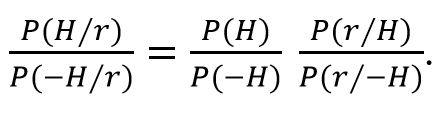
P (H/r) je vjerojatnost da je hipoteza H istinita pod uvjetom da je eksperiment dao rezultat r  (tzv. aposteriorna vjerojatnost od H ili njezin posterior).

P (–H/r) je vjerojatnost da je hipoteza H neistinita pod uvjetom da je eksperiment dao rezultat r  (tzv. aposteriorna vjerojatnost od –H ili njezin posterior).

P (H) je vjerojatnost da je hipoteza H istinita neovisno od eksperimenta (tzv. apriorna vjerojatnost od H ili njezin prior).

P (–H) je vjerojatnost da je hipoteza H neistinita neovisno od eksperimenta (tzv. apriorna vjerojatnost od –H ili njezin prior).

P (r/H) je vjerojatnost da eksperiment da rezultat r pod uvjetom da je hipoteza H istinita.

P (r/–H) je vjerojatnost da eksperiment da rezultat r pod uvjetom da je hipoteza H neistinita.

Hipoteza H je rezultatom eksperimenta r to bolje potvrđena što je P (H/r) veći u odnosu na P (–H/r). Dakle izraz s lijeve strane Bayesove formule treba biti što veći da bi hipoteza bila što vjerojatnija. Kada vjerujemo u pravilo p < 5% zapravo vjerujemo da je P (r/–H) < 5% dovoljan uvjet da lijeva strana bude velika (naime, P (r/–H) zapravo je p-vrijednost). No, očito je da veličina od P (H/r)/P (–H/r) ne ovisi samo o P (r/–H) pa ta vrijednost sama po sebi ne znači mnogo. Na primjer, ako je P (–H) bitno veća od P (H), onda čak i kada je P (r/H) veća od P (r/–H), činjenica da je P (r/–H) < 5% ne govori ništa o P (H/r)/P (–H/r). Drugim riječima, ako prije eksperimenta imate valjane razloge da hipotezu H držite malo vjerojatnom (tj. da omjer apriornih vjerojatnosti P (H)/P (–H) držite malim) onda p < 5% nije nikakav argument.

To i nije naročito složen zaključak pa zaista čudi da je itko ikada pomislio da je p < 5% nekakav argument. Problem je u tome što su mnogi (tzv. frekventisti) mislili da vjerojatnosti hipoteza (P (H/r), P (–H/r), P (H) i P (–H)) uopće nemaju smisla. Dakle, problem je u tome što je vjerojatnost nekog događaja i kako je odrediti. Na primjer, kako odrediti vjerojatnost da rezultat bacanja kovanice bude glava?

Ako o kovanici ne znamo ništa, vjerojatnost glave može biti bilo što između  H = 0 i H = 1 (između ta dva ekstrema leži i slučaj ‘poštene’ kovanice H = 1/2). Naivni način određenja te vjerojatnosti jest da je identificiramo s relativnom frekvencijom. Dakle, kovanicu bacimo npr. 12 puta, pa ako je 3 puta pala glava utvrdimo da je ta vjerojatnost 3/12, tj. H = 1/4. To je naivno,  jer svatko zna da i „poštena“ kovanica s H = 1/2 može u 12 bacanja dati 3 glave. Dakle, kako na temelju obavljenog eksperimenta, 3 glave u 12 bacanja, možemo procijeniti je li vjerojatnost glave 1/2 (ili 1/4 ili što već želimo procijeniti).

To Fisherova metoda testiranja hipoteza (npr. hipoteze da je H = 1/2) čini na sljedeći način:

1. Provedemo eksperiment, tj. kovanicu bacimo unaprijed zadani broj puta, na primjer 12 puta.
2. Odredimo prostor mogućih ishoda tog eksperimenta. U našem slučaju to je 2¹² nizova glava i pisama duljine 12. Rezultat eksperimenta jedan je od tih ishoda, npr. PPGPPPGGPPPP.
3. Rezultat eksperimenta sažmemo u jedan numerički podatak r, u ovom slučaju to je broj glava koje se pojavljuju u ishodu eksperimenta. Taj sažeti podatak o rezultatu eksperimenta zove se statistika testa. U našem primjeru r = 3.
4. Izračunamo vjerojatnosti svih mogućih statistika, pod uvjetom da vrijedi naša hipoteza H = 1/2 koja se naziva nul-hipotezom. Sve te vjerojatnosti P (r/H), za r = 0, 1, 2, …, 12 i H = 1/2, označimo kraće s P (r) i elementarnim računom nađemo

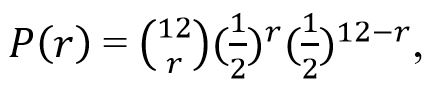
što daje sljedeću razdiobu tih vjerojatnosti:

r	P (r)	r	P (r)	r	P (r)	r	P (r)
0	0.0002441406	3	0.053710938	6	0.225585938	9	0.053710938
1	0.0029296875	4	0.120849609	7	0.193359375	10	0.0161132813
2	0.0161132813	5	0.193359375	8	0.120849609	11	0.0029296875
						12	0.0002441406

5. Pogledamo rezultate koji su se mogli pojaviti, a koji su uz našu nul-hipotezu ekstremniji od rezultata koji se uistinu pojavio. Preciznije, to su rezultati čija je vjerojatnost manja ili jednaka vjerojatnosti rezultata koji se stvarno pojavio. Izračunamo vjerojatnost p da dođe do takvog ekstremnog rezultata. U našem se primjeru stvarno pojavilo r = 3 glave, u 12 bacanja, pa su „ekstremni rezultati“ r = 0,1,2,3,9,10,11,12. To su podvučene vrijednosti u gornjoj razdiobi. Dakle, p je zbroj svih podvučenih vrijednosti, tj. p = 0.15 = 15%.
6. Nul-hipoteza se odbacuje ako je p < 5%. Dakle, naša nul-hipoteza o „poštenoj“ kovanici nije odbačena našim eksperimentom, jer je 15% > 5%.

Neki statističari preporučuju 1% ili čak 0.1% kao kritičnu vrijednost p. Prihvaćena kritična vrijednost zove se razinom signifikantnosti testa, a za nul-hipotezu se kaže da je odbačena na toj razini signifikantnosti, ako je vrijednost p manja ili jednaka prihvaćenoj kritičnoj vrijednosti.

Razmislimo što zapravo znači da je „nul-hipoteza odbačena na nekoj razini signifikantnosti“. To znači da je rezultat eksperimenta pao u određeno područje, koje je proglašeno „područjem odbacivanja“. Što to govori o nul-hipotezi? Danas je standardno gledište (uveo ga je J. Neyman) da odbacivanje ili ne odbacivanje nul-hipoteze nije nikakav matematički (čak ni induktivni) zaključak, nego tek „instrukcija o induktivnom ponašanju“. Ako se, uz razinu signifikantnosti 1%, ponašamo prema toj instrukciji onda ćemo u prosjeku, na duge staze, istinitu hipotezu odbaciti (tj. učiniti ćemo grešku I. tipa) ne više od jednom u 100 puta.

(Možemo se, kao J. Neyman i E. Pearson, brinuti i o greškama II. tipa, tj. o prihvaćanju neistinite hipoteze. Vjerojatnost greške II. tipa je vjerojatnost odbacivanja istinite alternativne hipoteze H_a, prihvaćanjem neistinite nul-hipoteze H₀. Komplement razine signifikantnosti odbacivanja  hipoteze H_a zove se snagom testa (dok se, u tom kontekstu, razina signifikantnosti odbacivanja nul-hipoteze H₀ zove veličinom testa). Idealno bismo trebali maksimizirati snagu i minimizirati veličinu testa. No, taj je ideal nekonzistentan. Smanjenje veličine testa sa sobom nosi povećanje njegove snage i obratno.)

Osim proizvoljnosti određenja ‘područja odbacivanja’, nekonzistentnosti redukcije veličine i ekspanzije snage testa, te ispitivanja samo jedne hipoteze, Fisherova metoda ima i drugih problema. Na primjer, različito izabrane statistike testa mogu iz istog eksperimentalnog rezultata izvesti različite zaključke. To je zloglasni problem ‘izbora statistike’.

Tu je i problem ‘pravila zaustavljanja’. Razmislimo opet o kovanici bačenoj 12 puta, s ishodom koji sadrži 3 glave i 9 pisama. Gore opisani test ne možemo ni početi primjenjivati ako ne znamo je li eksperimentator planirao kovanicu baciti točno 12 puta. Što ako ju je planirao bacati do pojave 3 glave ili dok mu ne dosadi bacanje? Tada prostor mogućih ishoda iz 2. koraka izgleda drukčije, s time i svi preostali koraci, pa i zaključak. Činjenica da su se u 12 bacanja pojavile 3 glave nije dovoljna. Moramo znati kako je zamišljen eksperiment koji je doveo do tog rezultata, sam rezultat nije dovoljan.

No, ključni problem Fisherove metode je da evaluira samo jednu hipotezu, tzv. nul-hipotezu (u našem primjeru „poštenje“ kovanice), uzimajući u obzir sve rezultate eksperimenta, koji su se mogli desiti. A nas zapravo zanima evaluacija svih mogućih hipoteza, na temelju jednog jedinog rezultata eksperimenta, koji se stvarno desio.

Laplace je uveo bitno informativniju metodu koja je povijesno prethodila Fisherovoj i bila je matematički objašnjiva. Pierre-Simon Laplace (Wikipedia)

Zar ne postoji metoda koja evaluira to što nas zanima? Postoji, i čak je prethodila Fisherovoj. Bitno je informativnija i matematički objašnjiva. Uveo ju je Laplace. Najprije ćemo pokazati kako se njome rješava naš problem testiranja kovanice, a zatim objasniti zašto ju je zamijenila neinformativna i matematički neobjašnjiva Fisherova metoda.

Laplace bi problem kovanice rješavao primjenjujući Bayesov teorem (nije bitno da razumijete tu metodu, bitno je da vidite što je njen rezultat). Ako prije eksperimenta nemamo nikakvog razloga da preferiramo bilo koju vrijednost H ∈ [0,1], kao vjerojatnost glave, onda je vjerojatnost P (H) (prije eksperimenta) uniformno distribuirana (sve hipoteze H su jednako vjerojatne):

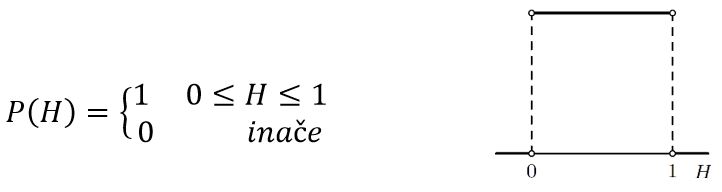
Bacimo li kovanicu jednom i padne li glava G, Laplace bi iz Bayesove formule izračunao da je P (H/G), tj. vjerojatnost hipoteze H (koja tvrdi da vjerojatnost glave iznosi H), nakon što je jednom pala glava, distribuirana na sljedeći način:

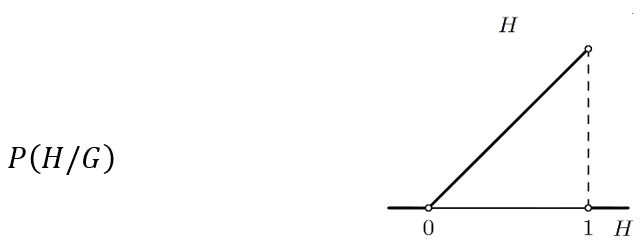
Dakle, vjerojatnost hipoteze H uniformno raste kada H raste od 0 do1 (najmanja je za H = 0, a najveća za H = 1, ali i druge hipoteze H imaju svoje vjerojatnosti).

Bacimo li kovanicu još jednom i padne li opet glava, vjerojatnost hipoteze H nakon što je dva puta pala glava, P(H/GG), distribuira se prema Bayesovoj formuli na sljedeći način:

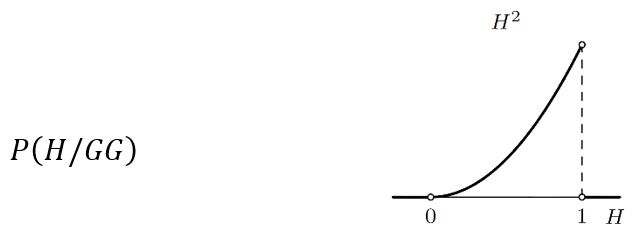
Padne li treći put pismo P, vjerojatnost hipoteze H, nakon što je dva puta pala glava i jednom pismo, distribuira se prema Bayesovoj formuli na sljedeći način:

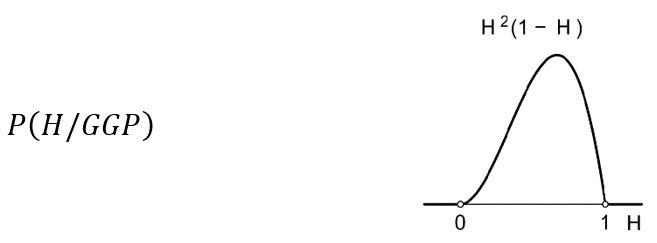
Još jedno pismo i vjerojatnost hipoteze H distribuira se na sljedeći način:

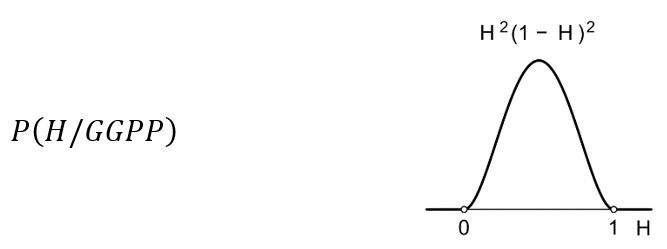
I tako dalje. Sljedeće slike pokazuju kako se distribucija vjerojatnosti hipoteze H mijenja sa sve više i više podataka o rezultatima bacanja kovanice. Položaj maksimalne vjerojatnosti sve se više stabilizira što je broj podataka veći. Osim toga, sa sve većim brojem podataka distribucija postaje sve uža i uža. Nakon 1000 bacanja s 310 glava i 690 pisama vjerojatnost da je H = 1/4 daleko je najveća. Primijetite da je za svaki H ∈ [0,1] izračunata vjerojatnost toga H.

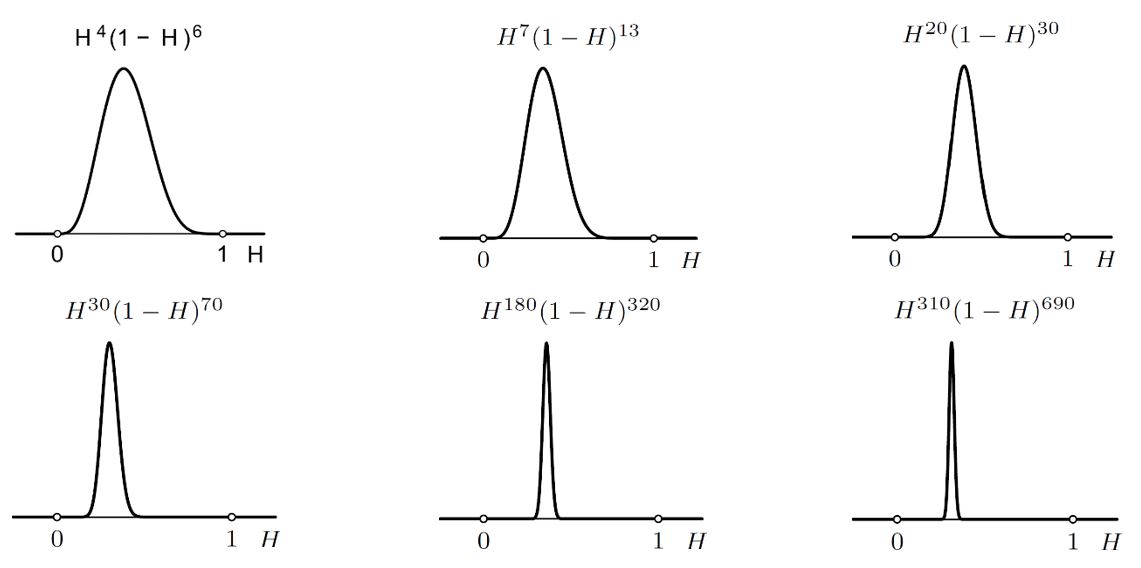
Što bi bilo da smo krenuli od nekog druge početne distribucije hipoteza H, a ne od uniformne (npr. da smo prije eksperimenta izučavanjem kovanice zaključili da je H > 1/2 vjerojatnije nego H < 1/2). Uz isti niz dobivenih glava i pisama dobili bismo isti rezultat. Naime, naše preduvjerenje o kovanici u početku bi snažno utjecalo na distribuciju od H (ako ste uvjereni da je kovanica „poštena“, tj. da je  H = 1/2, onda vas 3 glave u 12 bacanja neće pokolebati), no kako broj bacanja raste rezultati bacanja nadjačaju sva preduvjerenja (30 000 glava u 120 000 bacanja, pokolebati će vašu vjeru u H = 1/2). To je intuitivno jasno, a matematički slijedi iz Laplaceove primjene Bayesovog teorema.

Primijetimo još jednom, da za razliku od Fisherove metode koja odbacuje ili ne odbacuje samo jednu hipotezu (u našem primjeru hipotezu da je H = 1/2), Laplaceova metoda daje vjerojatnost za svaki H, dakle za svaku moguću hipotezu. To je točno ono što smo htjeli.

Kako je uopće došlo do toga da Fisherova ograničena, neprecizna i nematematička metoda zamijeni Laplaceovu generalnu, preciznu i matematičku metodu?

Frekventisti drže da je hipoteza je istinita ili lažna, a ne nešto što može biti manje ili više vjerojatno.

Laplaceova metoda temelji se na tome da su vjerojatnosti racionalne procjene uvjerenja koje se temelje na raspoloživim podacima. Nije odmah jasno zašto bi tako shvaćene vjerojatnosti zadovoljavale uobičajene aksiome vjerojatnosti, koje su Laplace i njegovi sljedbenici koristili i iz kojih slijedi Bayesov teorem. Ako vjerojatnosti shvatimo kao granične relativne frekvencije, te je aksiome lako dokazati, iako je sam pojam granične relativne frekvencije nekonzistentan. Statističari s kraja 19. i s početka 20. stoljeća počeli su insistirati da se vjerojatnosti moraju shvaćati isključivo kao granične relativne frekvencije u tzv. slučajnim eksperimentima. Nažalost, takvo shvaćanje vjerojatnost hipoteze čini nelegitimnim pojmom; hipoteza je istinita ili lažna, ona nije nešto što može biti manje ili više vjerojatno. Dakle, hipoteza  H = 1/2 istinita je ili je lažna i nema smisla govoriti o vjerojatnosti hipoteze H = 1/2. No, baš to da hipoteze mogu biti manje ili više vjerojatne temelj je Laplaceovog pristupa. Ako odbacimo taj temelj zaglibit ćemo u Fisherovoj metodi.

Spomenimo na kraju da od 50-tih godina 20. stoljeća znamo da vjerojatnost shvaćena kao „racionalna procjena uvjerenja koje se temelji na raspoloživim podacima“ zadovoljava standardne aksiome vjerojatnosti. To je dokazano Coxovim teoremom i više nema razloga  da ograničenu, nepreciznu i nematematičku Fisherovu metodu upotrebljavamo umjesto generalne, precizne i matematičke Laplaceove metode. Više o svemu tom u https://eujap.uniri.hr/volume-10-no-1-2014/ .