Aristotelova silogistika. Jednostavna i jedina simbolička logika kroz dva milenija

Aristotelova silogistika bila je prva formalna logička teorija, a dvije tisuće godina bila je i jedina simbolička logika, piše Zvonimir Šikić. Ona se može svesti na jednostavnu primjenu Vennovih dijagrama, no bitna je kako bi se jasnije predočio napredak na polju logike u proteklih sto pedeset godina.

• Naslovna fotografija: Aristotel razmišlja o Vennovim dijagramima, u stilu crteža olovkom. (Midjourney v7)

• Prethodni članci u seriji: Formalizacije logike sudova. Frege i Kneale, generatori i testovi, Logička korektnost, potpunost i kompaktnost. Gentzenov IF-sustav i Bethova semantička stabla, Zaključivanje u prirodnom i artificijelnom jeziku. Od Aristotela prema Fregeu, Logika sudova. Kondicionali, bikondicionali i implikacije

­

1. Kategoričke forme i klasična silogistika

Svi prirodni jezici sadrže operatore pomoću kojih se iz pojmova grade deklarativne rečenice. Četiri takva operatora istražio je Aristotel u svojoj silogistici, prvoj formalnoj logičkoj teoriji. Ona se bavi tzv. kategoričkim tvrdnjama koje su oblika

­­

Kategoričke forme (A) i (I) su afirmativne, dok su (E) i (O) negativne. S druge strane, (A) i (E) su univerzalne, dok su (I) i (O) partikularne. Otuda i njihove skolastičke oznake (prva dva vokala riječi afirmo koriste se za univerzalnu i partikularnu afirmativnu formu, a prva dva vokala riječi nego koriste se za univerzalnu i partikularnu negativnu formu).

Atomarne forme S i P, u kategoričkim formama stoje na mjestu općih pojmova. Oni se zovu subjekt i predikat i u prirodnim se jezicima izražavaju na razne načine. Često su to imenice kao u: Neki logičari su filozofi. No, to mogu biti i pridjevi, glagoli ili prilozi kao u: Neki logičari nisu mudri. Sve ptice lete. Neki ne trče brzo. U svim slučajevima radi se o pojmovima (“logičar”, “filozof”, “mudra osoba”, “ptica”, “ono što je brzo”). Opći pojam se u prirodnom jeziku može izraziti i složenom frazom, npr. “onaj koji je igrao na tri svjetska prvenstva u nogometu”.

Usprkos svoj toj šarolikosti pojmovi su bitno različiti od tvrdnji. Tvrdnje su istinite ili neistinite. Pojmovi su istiniti o mnogim stvarima, jednoj stvari, ili možda čak nijednoj, a neistiniti o svim ostalim stvarima. Pojam “žena” istinit je o svim ženama i ni o čemu drugom, “zemljin mjesec” je istinit samo o jednoj stvari, a “okrugli kvadrat” ni o jednoj.

Umjesto nespretne fraze da je pojam o nečemu istinit ili neistinit, češće se govori da nešto je ili nije u njegovom opsegu ili ekstenziji. Dakle, svaka žena je u opsegu pojma “žena” i ništa nije u opsegu pojma “okrugli kvadrat”. Ekstenzija nekoga pojma često se identificira sa skupom svih stvari u njegovoj ekstenziji (no, logika pojmova ni na koji način ne pretpostavlja postojanje apstraktnih skupova kojima se bavi teorija skupova; neki njezini pojmovi čak ni nemaju ekstenziju u skupovnom smislu).

Četiri Aristotelova operatora, “svi su”, “nijedan nije”, “neki su” i “neki nisu”, primijenjeni na pojmove S i P daju kategoričke forme A, E, I, O. Aristotela su zanimali argumenti koji su poznati kao kategorički silogizmi i kojima se iz dvije kategoričke premise izvodi kategorička konkluzija.

Aristotel je sve moguće silogizme razvrstao u sljedeće četiri figure.

Figura:	I	II	III	IV
Glavna premisa:	MP	PM	MP	PM
Sporedna premisa:	SM	SM	MS	MS
Konkluzija:	SP	SP	SP	SP

U svakom silogizmu su sa S i P označeni subjekt i predikat konkluzije. Oni se zovu sporednim i glavnim pojmom silogizma. Premise sadrže zajednički pojam, označen s M, koji se zove srednjim pojmom silogizma. Prva ili glavna premisa sadrži glavni pojam P, a druga ili sporedna premisa sadrži sporedni pojam S. Na primjer,

­­

jedan je od silogizama druge figure. Kraće ga označavamo s II IAE, jer pripada drugoj figuri, glavna mu je premisa oblika I, sporedna oblika A, a konkluzija oblika E.

Silogizama ima ukupno 4 · 4³ = 256. Naime, dvije premise i konkluzija (njih 3) mogu biti u bilo kojem od oblika A, E, I, O (njih 4), što je 4³ moguća silogizma u svakoj od 4 figure. To je ukupno 4 · 4³ silogizama. Osnovni je zadatak silogistike ustanoviti koji su od tih 256 silogizama valjani, tj. u kojima premise impliciraju konkluziju.

Aristotel ih je našao 14, njegov učenik Teofrast još pet, a Ariston iz Aleksandrije još pet . To su ukupno 24 valjana silogizma. Aristotel je 4 valjana silogizma I. figure (kasnije nazvana Barbara, Celarent, Darii, Ferio, v. dalje) smatrao očitim aksiomima, a ostale je dokazivao svođenjem na te aksiome. Skolastici su kao mnemotehniku za 19 valjanih silogizama i njihova svođenja koristili pjesmicu:

Barbara, Celarent, Darii, Ferioque prioris

Cesare, Camestres, Festino, Baroco secundae

Tertia grande sonans recitat Darapti, Felapton

Disamis, Datisi, Bocardo, Ferison. Quartae

Sunt Bamalip, Calames, Dimatis, Fesapo, Fresison.

Stihovi se ne poklapaju s figurama (III i IV figura se nalazi u zadnja tri stiha) pa radi lakšeg objašnjenja pjesmice izdvajamo ključne riječi po figurama i dodajemo podvučene riječi za Aristonove silogizme kojih nema u izvornoj pjesmici, ali se pojavljuju u njenim kasnijim verzijama.

I  Barbara, Celarent, Darii, Ferio, Barbari, Cesaro

 II  Cesare, Camestres, Festino, Baroco, Celaront, Camestrop

III  Darapti, Felapton, Disamis, Datisi, Bocardo, Ferison

IV  Bamalip, Calames, Dimatis, Fesapo, Fresison, Camenop

Svaka je riječ kodirani zapis valjanog silogizma koji treba tumačiti u skladu sa sljedećim pravilima:

• prva tri samoglasnika u riječi označavaju koje su vrste tri kategorička suda koji čine silogizam, npr. Darii označava (AII);
• početni suglasnik svake riječi za II, III i IV figuru označava da se njen silogizam svodi na silogizam I figure koji počinje isti početnim slovom;
• suglasnik s koji se pojavljuje odmah nakon samoglasnika označava da  odgovarajući sud pri svođenju na I figuru treba konvertirati (zamijeniti njegov subjekt i predikat);
• suglasnik p na istom položaju označava da odgovarajući sud treba konvertirati i partikularizirati („svi“ i „nijedan“ promijeniti u „neki“);
• suglasnik m između prva dva samoglasnika označava da odgovarajuće premise trebaju zamijeniti mjesta;
• suglasnik c  koji se pojavljuje između dva samoglasnika označava da konkluziju treba zamijeniti njenom negacijom te iz nje i jedne premise (uz aksiomatski silogizam određen prvim slovom) izvesti negaciju druge premise, što redukcijom ad absurdum dokazuje valjanost silogizma;
• ostali suglasnici nemaju nikakvo značenje.

Na primjer, Cesare u II figuri (s vokalima e, a, e) predstavlja silogizam II EAE:

­­

Suglasnik s (koji je u Cesare nakon e) daje uputu da e-premisu zamijenimo njoj ekvivalentnom konverzijom. Tako dobivamo ekvivalentni silogizam I EAE, koji je aksiomatski valjani Celarent:

­­

Dakle, Cesare iz II figure sveden je na Celarent  iz I figure konverzijom prve premise (tj. Cesare slijedi iz Celarent konverzijom prve premise).

Baroco u II figuri (s vokalima a, o, o) predstavlja silogizam II AOO:

­­

Suglasnik c daje uputu da pretpostavimo negaciju konkluzije: Nije da neki S nisu P . Ona je ekvivalentna sa Svi S su P.  To zajedno s prvom premisom, prema kodiranom zapisu Barbara  iz I figure, implicira Svi S su M, što je u kontradikciji s drugom premisom. Dakle ne vrijedi negacija konkluzije, tj. Baroco slijedi iz Barbara redukcijom ad apsurdum.

Ta je skolastička mnemotehnika zapravo fascinantna. Od 169 slova u 24 imena koja kodiraju valjane silogizme, samo njih 44 (što je cca 25%) nema neku funkciju.

2. Vennovi dijagrami

Mnogo je jednostavnija Vennova metoda, kojom lako možemo za svaki silogizam odlučiti je li on valjan ili nije. Naime, metoda jasno pokazuje koju konkluziju impliciraju zadane premise.

Kategoričke forme prikazujemo na sljedeći način, tzv. Vennovim dijagramima.

­­

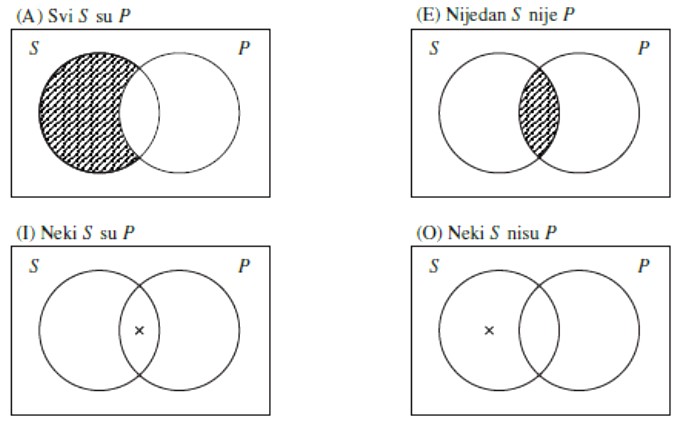
Iscrtkavanje područja znaci da u tom području nema ničega. Križić u području znači da u tom području ima nečega. (Primijetimo da iscrtkavanje daje univerzalne tvrdnje, a križić partikularne). Bjelina u području ne znači ništa do odsustvo bilo kakve informacije o tom području.

Najjednostavnija svojstva kategoričkih tvrdnji lako se iščitavaju iz njihovih dijagrama. Simetrija dijagrama E i I znači da redoslijed pojmova u odgovarajućim tvrdnjama nije bitan. “Nijedan S nije P” znači isto što i “nijedan P nije S “, kao što i “neki S su P” znači isto što i “neki P su S “. (Ako su neki filozofi logičari, onda su neki logičari filozofi i obratno. Ako nijedan logičar nije kralj, onda nijedan kralj nije logičar i obratno.) Takvu zamjenu subjekta i predikata skolastici su zvali konverzijom. Naravno, konverzija nije dopustiva u tvrdnjama oblika A i O, što se vidi iz asimetrije odgovarajućih dijagrama. “Svi S su P” ne znači isto što i “svi P su S “, niti “neki S nisu P” znači isto što i “neki P nisu S “. (Svi logičari su ljudi, ali nisu svi ljudi logičari. Neki ljudi nisu logičari, ali nije istina da neki logičari nisu ljudi.)

Tvrdnje oblika A i O ( s istim subjektom i predikatom) međusobno su kontradiktorne, tj. jedna je negacija druge. Naime, O dijagram ima križić točno tamo gdje je A dijagram iscrtkan. Isto vrijedi za tvrdnje E i I; E je istinita akko je I neistinita.

Tvrdnje oblika A i E ( s istim subjektom i predikatom) također su na neki način suprotstavljene. Skolastici su ih zvali međusobno kontrarnima. No kontrarno nije kontradiktorno, tj. E nije negacija od A. “Svi ljudi su generali” jednako je neistinito kao i “nijedan čovjek nije general”. Isto vrijedi i za tvrdnje I i O. “Neki ljudi su generali” jednako je istinito kao i “neki ljudi nisu generali”.

Kontrarne tvrdnje A i E često su obje neistinite, kao što su kontrarne tvrdnje I i O često obje istinite. Mnogo je rjeđe da su A i E obje istinite ili I i O obje neistinite. Jednim pogledom na njihove dijagrame vidimo da to vrijedi samo ako ne postoji S . Jasno, ako ne postoji S onda je neistinito “neki S su P” i “neki S nisu P”. Bez uvida u dijagrame nešto je manje očigledno da su u odsustvu S-ova tvrdnje “svi S su P” i “nijedan S nije P” obje istinite. Naime, mnogi smatraju da te tvrdnje podrazumijevaju da postoji S . To je konvencija koja se može prihvatiti, ali u logici ona nije prihvaćena jer bi implicirala da A i O te I i E nisu međusobno kontradiktorne forme, što bi otežavalo formulacije mnogih logičkih pravila. Dakle, “svi S su P” uvijek znači “ne postoji S koji nije P”.

Važna posljedica te logičke konvencije je da “svi S su P” ne implicira „neki S su P”, što se vidi na dijagramima od A i I (na A dijagramu nema informacije koja je na I dijagramu). Naravno, “neki S su P” slijedi iz “svi S su P” i “postoji S “, jer te dvije premise imaju sljedeći dijagram.

­­

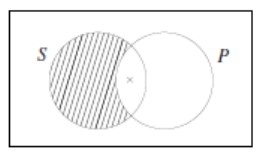
Premise kategoričkog silogizma prikazujemo zajedničkim Vennovim dijagramima koji reprezentiraju tri pojma S , M i P na sljedeći način.

­­

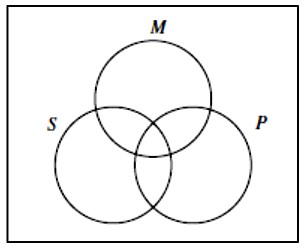
Odgovarajućim križićima i/ili iscrtkavanjima prikazujemo 1. i 2. premisu silogizma, pa iz tako dobivenog Vennovog dijagrama iščitamo njegovu konkluziju, gledajući kako su križići i/ili iscrtavanja smješteni u odnosu na S i P.

Slijedi po jedan primjer Vennovog izvođenja u svakoj od četiri figure.

­­

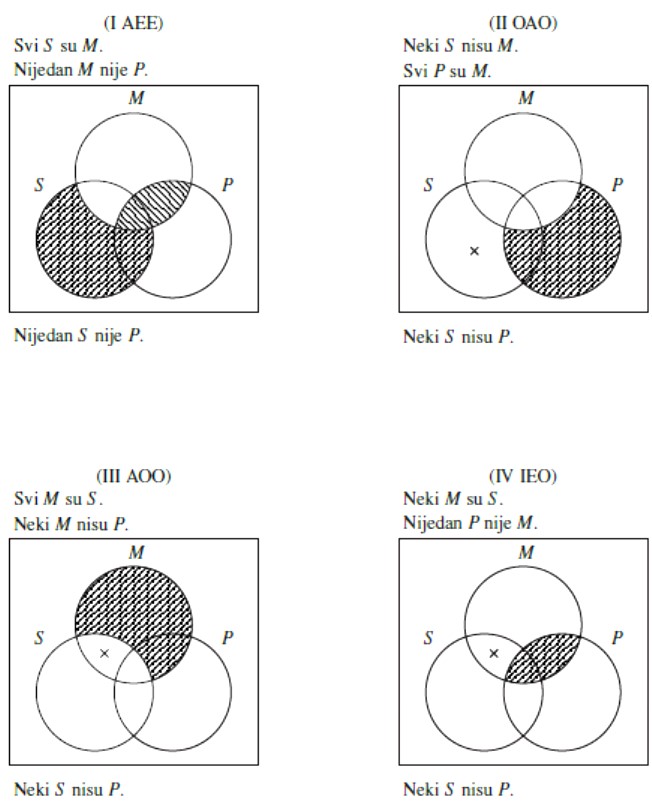
Tako možemo provjeriti svaki od 256 kategoričkih silogizama, te naći one koji su valjani. To možemo ubrzati primjenom sljedećih principa čija je korektnost lako provjeriva Vennovim dijagramima.

• “Valjana konkluzija je univerzalna samo ako su to i obje premise”.
• “Valjana konkluzija je afirmativna samo ako su to i obje premise”.
• “Valjani silogizam sadrži bar jednu univerzalnu premisu”.
• “Valjani silogizam sadrži bar jednu afirmativnu premisu”.

Tako bismo došli do sljedećih 15 valjanih silogizama.

U I figuri valjani su silogizmi AAA, EAE, AII i EIO:

­­

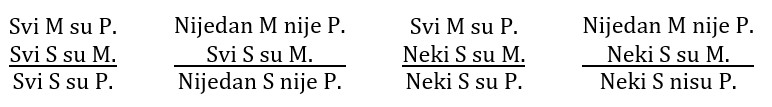
U II figuri valjani su silogizmi EAE, AEE, EIO i AOO:

­­

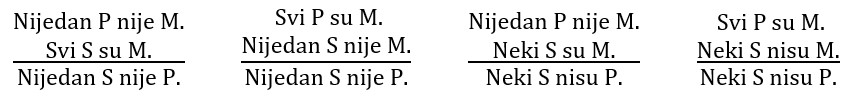
U III figuri valjani su silogizmi IAI, AII, OAO i EIO:

­­

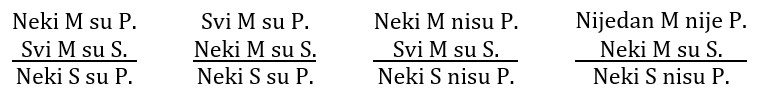
U IV figuri valjani su silogizmi AEE, IAI, EIO:

­­

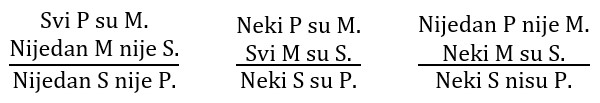
Antički i skolastički logičari valjanima su smatrali još 9 silogizama, jer su pretpostavljali da uvijek postoji bar jedan P, S i M. I njih je lako provjeriti Vennovim dijagramima.

U I figuri to su AAI i EAO:

­­

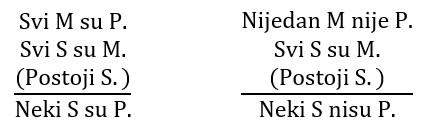
U II figuri to su AEO i EAO:

­­

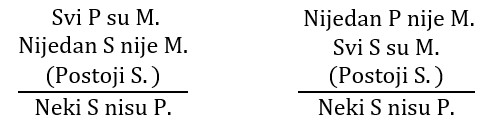
U III figuri to su AAI i EAO:

­­

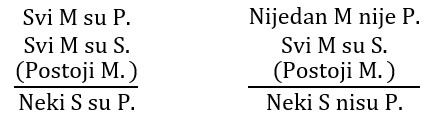
U IV figuri to su AEI, EAO i AAI:

­­

Tradicionalno se i neki zaključci koji uključuju singularne tvrdnje svrstavaju u silogizme, Na primjer, valjani zaključak

­­

smatra se primjerkom valjanog silogizmom I AAA. Naime, singularna tvrdnja „Sokrat je smrtan“ ima formu „Svi S su P“ ako se S shvati kao „biti identičan Sokratu“. Vidjet ćemo da moderna logika imena (singularne termine) razumijeva na bitno različit način.

Zaključimo. Aristotelova silogistika svodi se na jednostavnu primjenu Vennovih dijagrama i zapravo je krajnje jednostavna. Njome smo se bavili samo zato što je dvije tisuće godina bila jedina simbolička logika te da bismo jasnije vidjeli razmjere napretka koji je logika učinila u zadnjih sto pedeset godina. Od Boolea i Fregea do danas.