Dvanaest veličanstvenih. Matematika glazbene oktave

U svojem eseju o matematici podjele tonova unutar oktave, Zvornimir Šikić ulazi duboko u povijest razvoja muzičkih skala, prolazi kroz eksperimentiranja s različitim modusima i skalama, te pojašnjava zašto je u modernoj muzici uvriježena dodekatonska, kromatska skala.

• Naslovna fotografija: Klavijatura (Elliott Billings / CC BY 2.0)

• Intervali i skale

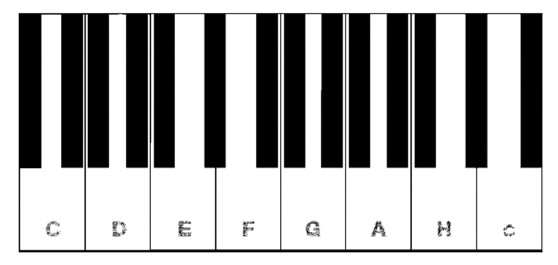
Pojam intervala i iz njega izvedeni pojam skale (ljestvice) iznimno su važni u teoriji muzike, a ključni su i za razumijevanje njezinog povijesnog razvoja. Zamislimo segment klavirskih tipki koji se na klaviru periodički ponavlja i koji sadrži po jednu tipičnu grupu od 2 i 3 crne tipke unutar 8 bijelih.

Niz od 8 “bijelih” tonova C, D, E, F, G, A, H, c (tzv. dijatonska skala) svima je dobro poznata dur ljestvica; u ovom slučaju C-dur. Interval oktave, od C do c, sadrži 8 ‘bijelih’ tonova. Interval kvinte, od C do G, sadrži 5 “bijelih” tonova. Interval kvarte, od C do F, sadrži 4 “bijela” tona. No, kako je nastala “bijela” dur ljestvica?

Uz dogovor da je frekvencija tona C jedinična, imamo sljedeće frekvencije:

C = 1, F = 4/3, G = 3/2 i c = 2.

Veličina intervala koji razapinju dva tona jednaka je omjeru njihovih frekvencija, što je prikazano sljedećom skicom:

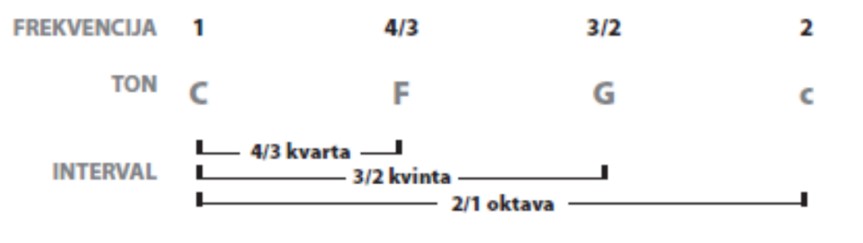
Sada je lako izračunati i veličine sljedećih intervala:

\(
\Large{\frac{c}{F} = \frac{2}{\frac{4}{3}} = \frac{3}{2}} \quad \Large{\frac{c}{G} = \frac{2}{\frac{3}{2}} = \frac{4}{3}} \quad \Large{\frac{G}{F} = \frac{\frac{3}{2}}{\frac{4}{3}} = \frac{9}{8}}
\)

Dakle, c je kvinta na F i c je kvarta na G. Interval od F do G, veličine 9/8 (ili 204 centa, v. dolje), zove se cijeli ton ili velika sekunda.

Kvarta i kvinta čine sljedeću razdiobu oktave:

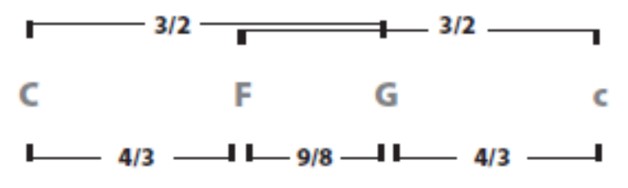
Ako donju kvartu od C do F, te gornju kvartu od G do c, razdijelimo cijelim tonovima duljine 9/8, dobit ćemo još po dva tona u svakoj od njih:

D/C = 9/8, tj. zbog C = 1, D = 9/8.

E/D = 9/8, tj. zbog D = 9/8, E = 81/64.

A/G = 9/8, tj. zbog G = 3/2, A = 27/16.

H/A = 9/8, tj. zbog A = 27/16, H = 243/128.

Tako dolazimo do sljedeće razdiobe oktave:

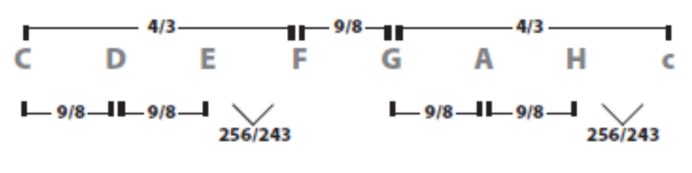
Interval od E do F, kao i interval od H do c, ima duljinu 256/243, jer je

\(
\Large{\left(\frac{4}{3}\right) / \left(\frac{9}{8}\right)^{2} = \frac{256}{243}}
\).

Taj interval (koji ima 90 centi, v. dolje) zove se dijatonski poluton.

Ovako dobiveni cijeli tonovi i polutonovi imaju loše svojstvo da su dva polutona manja od jednog cijelog tona:

\(
\Large{\left(\frac{256}{243}\right)^{2}=1.110 < 1.125 = \frac{9}{8}}
\).

Oktava se može podijeliti i na druge načine. Najpoznatiji su modusi ili modalne skale koji se mogu odsvirati na bijelim tipkama klavira, polazeći od različitih osnovnih tonova. Grci su koristili Jonski modus iz C (dakle dur), Dorski iz D, Frigijski iz E, Lidijski iz F, Miksolidijski iz G,  Eolski iz A i Lokrijski iz H. Naravno, oktava se može podijeliti i skalama koje nisu “bijele“. Takvi su npr. uzlazni i silazni melodijski mol.

Happy Birthday  u svim modusima možete čuti ovdje:

Norwegian wood  koja je izvorno u miksolidijskom modusu, u svim je modusima ovdje:

Pentatonske skale, tj. skale koje oktavu dijele na 5 intervala (za razliku od do sada razmatranih heptatonskih skala koje je dijele na 7 intervala), najčešće ubacuju po jedan ton između tonike i kvarte te između kvinte i gornje tonike. Iako se termin pentatonska skala može upotrijebiti za bilo koju razdiobu oktave na 5 intervala, u Europi se taj termin ustalio za heptatonske „bijele“ skale iz kojih su izostavljeni “polutonovi” F i H.

Od heksatonskih skala, koje oktavu dijele na 6 intervala, najpoznatije su cjelotonska skala koja oktavu dijeli na 6 cijelih tonova i blues skala koja je dijeli na sljedeći način (uz očite oznake za cijeli ton, poluton i jedan i pol ton):

Primjer skladbe u blues skali, od Tracy Chapman, možete čuti ovdje:

Primjer Debussyjeve skladbe u cjelotonskoj skali možete čuti ovdje:

Povijest i rasprostranjenost ovih skala složene su. Dijatonska podjela oktave (na “bijele” tonove), koja je dovela do heptatonskih modusa seže do Pitagorina vremena. Upotreba lire i orgulja, koje je oko 300. g. pr.Kr. izumio Ktesibije iz Aleksandrije, a kojima je glavni ton u oba slučaja bio D, dovela je do prevlasti dorskoga modusa u glazbenoj antici. U ranom srednjem vijeku, u okviru scholae cantorum, kršćanska crkva nastavlja tradiciju monofonije (izvođenja samo jedne melodijske linije) u svim antičkim modusima. Grgurova reforma ove škole dovest će do gregorijanskog korala koji je i danas prepoznatljiv po svojoj uporabi antičkih modusa.

Primjer gregorijanskog korala možete čuti ovdje:

Na prijelazu iz 10. u 11. stoljeće počinju eksperimenti s polifonijom – istovremenim izvođenjem više melodijskih linija. Glasovi se slažu u paralelnom gibanju, tako da jedan izvodi svoju melodiju dok ga drugi prati, istovremeno izvodeći tu istu melodiju za kvartu ili kvintu niže. Dakle, tonovima prvoga glasa: C D E F G A H c, odgovaraju tonovi drugoga glasa: G A H C D E F g (koji su za kvartu niži) ili F G A H C D E f (koji su za kvintu niži). Glasovi su stalno udaljeni za kvartu (2.5 cijela tona), odnosno kvintu (3.5 cijela tona), osim kada istodobno pjevaju tritonus H/F (3 cijela tona). Tritonus je izrazito disonantan, a teško ga je i otpjevati. Zato bi pri susretu tonova H i F uvijek dolazilo do nesigurnosti koja se mogla otkloniti snižavanjem tona H za jedan poluton.

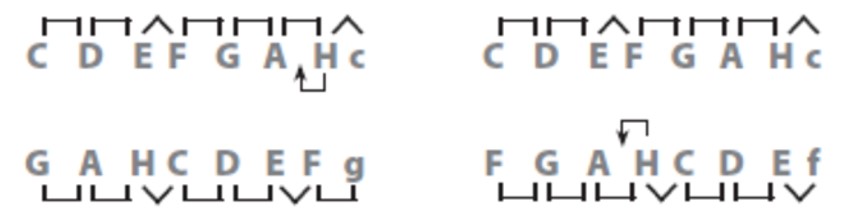
Tako su stari modusi prošireni notom B, a u klavijature je umetnuta prva crna tipka.

Primjer paralelnih kvinti (i zašto su danas „zabranjene“) možete čuti ovdje:

To je neko vrijeme bila jedina snižena nota i jedina crna tipka.

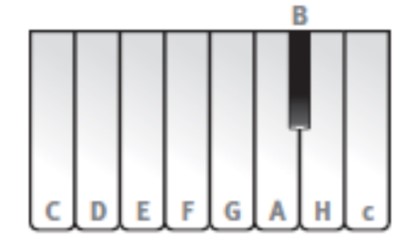
Možemo primijetiti da pomak iz H u B u prvom glasu ukida vođicu (završni polutonski interval koji prirodno zatvara muzičku frazu). Zato se boljim rješenjem čini pomak iz F u F^# u drugom glasu. Taj pomak otklanja disonantni tritonus, a ne ukida vođicu. Naravno, nove note B i F# prirodno vode prema novim kvintama:

E^b⟵B                F^#⟶C^#⟶G^#.

Tako je oktava konačno podijeljena na 12 polutonova, a klavijature su dobile još po 4 crne tipke unutar oktava:

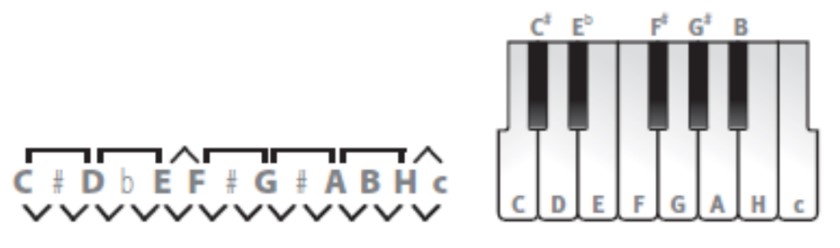
Ovaj proces nije neposredno doveo do “polutonskog” skladanja u tako dobivenoj dodekatonskoj (kromatskoj) skali. To će se dogoditi tek u 20. stoljeću. U tom smislu polutonska razdioba još dugo nije postala skalom. Ona je samo omogućavala polifonsko skladanje u starim heptatonskim modusima, jer se u njoj svaka stara skala mogla vezati uz bilo koji ton kao toniku (drugim riječima, nova je razdioba omogućavala transpozicije). Time su također otvorena vrata harmonijskom skladanju, koje zapravo nema jasne granice s polifonskim, budući da je istovremeni (vertikalni) aspekt polifonije, zapravo harmonija.

Protezanjem glazbe u dvije dimenzije stvoren je ogroman broj mogućnosti. U Europi 16. st. bilo je toliko velikih skladatelja da cijeli jedan život nije dovoljan za upoznavanje čak i dijela njihova opusa. Studenti polifonije, tj. kontrapunkta, još i danas uče iz tog nepresušnog vrela. Ipak, nakon nebrojenog niza eksperimenata sa svim tradicionalnim modusima, početkom 17. st. izdvojio se jedan: jonski. To je današnji dur. Ostali su modusi polako nestajali, osim modificirane varijante eolskog, koja je današnji mol. Za oba preživjela modusa karakteristična je velika septima, tzv. vođica, koja je samo pola tona udaljena od tonike i time je iznimno naglašava kao mjesto razrješenja svoje disonantne napetosti. Zaljubljenost vođice u toniku glavna je karakteristika preživjelih modusa. Od baroka do romantike oni su neprijeporno vladali zapadnom tonalnom, što zapravo znači toničkom, glazbom.

Skladatelji s početka 20. st. suočavaju se s novim dvojbama. Unendliche Melodie Richarda Wagnera

koja je zapravo melodija bez toničkoga kraja, i njeni “lutajući” akordi, doveli su tonalnu glazbu do samih granica tonalnosti (tj. toničnosti). Wagnerovi neposredni sljedbenici više nisu zadovoljni starim sustavom tonaliteta i njihovih odnosa. Oni su u potrazi za novim skalama bez izražene tonike. Debussy sklada u cijelo-tonskoj ljestvici bez izražene tonike

što njegovoj muzici daje smirenu, gotovo onostranu kvalitetu. Istu je skalu gotovo redovito rabio Thelonius Monk

i ona je još uvijek iznimno popularna u mnogim jazz krugovima. Schönberg i mnogi drugi skladatelji 20. st. upotrebljavaju kromatsku skalu

s efektima često stranima nenaviknutu uhu.

Međutim, zamjetan je i povratak tradicionalnim heptatonskim modusima, koji su dovoljno stari i dovoljno zaboravljeni da se opet mogu pojaviti kao svjež i nov zvuk. Kao zvuk starih, gotovo primitivnih vremena, ili kao bezvremenski zvuk gregorijanskih korala. Sibelius nas, na početku 6. simfonije

odvodi u stare finske šume upotrebljavajući dorski modus. Debussy, Hindemith i Stravinski često rabe dorsko odsustvo vođice kako bi postigli efekt svečanog, gotovo formalnog A-MEN (koji je cijelo-tonski C-D).

Isti efekt postiže se i frigijskim modusom. Njegova je dodatna karakteristika tužni i orijentalni prizvuk njegova polutonskog početka (E-F). Zato ga Rimski-Korsakov rabi u svojoj Šeherezadi kao i Brahms u polaganom stavku svoje 4. simfonije

Mnogo je “tužne” španjolske, ciganske i židovske glazbe skladano u frigijskom modusu, npr. Lisztova 2. mađarska, zapravo ciganska, rapsodija

Povišena kvarta lidijskog modusa djeluje kao pogrešan ton u običnom duru, gotovo šaljivo. Duhoviti Prokofjev baš će zato često rabiti lidijski modus. Inače je taj modus karakterističan za poljsku glazbu; kako za narodnu, tako i za Chopinove poloneze i mazurke. Polonezu iz 3. čina Borisa Godunova  Musorgski je napisao u lidijskom modusu

Miksolidijski modus je “dur sa sniženom septimom”, tj. “dur bez vođice”. To ga je činilo dovoljno neobičnim i novim da mu omogući ulazak u mnoge klasike rock-and-rolla, npr. You really got me od Kinksa i Norwegian wood od Beatlesa

Pentatonska skala C D E G A c (tzv. “crna” skala koja se, polazeći iz F#, može odsvirati na crnim tipkama kao F^# G^# B C^# D^#) koristi se u narodnoj glazbi širom svijeta. Preberete li nekoliko puta (u arpeggiu) pentatonski niz C D E G A c, u mislima će vam se pojaviti barem jedan od hitova zabavne glazbe (zabavna industrija zaradila je velike novce na ovih 5 nota). To je najčešća skala zabavne glazbe, koja problem tritonusa H/F rješava izbacivanjem nota H i F iz septatonske skale: C D E F G A H c.

To je minimalističkio rješenje za polifonsko i harmonijsko skladanje.

• Jednolikost i točnost

Vratimo se još jednom osnovnom glazbenom materijalu koji se sastoji od 12 polutonova kromatske skale (i iz kojeg svoj materijal odabiru sve skale obrađene u prethodnom poglavlju):

Dosad nismo temeljitije proučili problem veličine intervala u toj skali. Pitagorin ideal bio bi, osnovni ton C = 1/1, oktava c = 2/1, kvinta G = 3/2, kvarta F = 4/3 i terca E = 5/4. Iz toga slijedi:

\(
\Large{\frac{G}{F} = \frac{\frac{3}{2}}{\frac{4}{3}} = \frac{9}{8}} \quad \Large{\frac{F}{E} = \frac{\frac{4}{3}}{\frac{5}{4}} = \frac{16}{15}} \quad \Large{\frac{D}{C} = \frac{9}{8}} \quad \Large{\frac{E}{D} = \frac{\frac{5}{4}}{\frac{9}{8}} = \frac{10}{9}}
\)

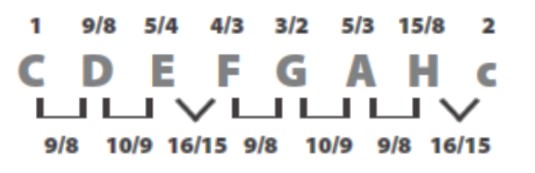
Tu skalu preporuča Ptolemej, najveći antički astronom i muzički teoretičar. Njeni su polutonovi duljine 16/15, dok su cijeli tonovi različitih duljina, 9/8 i 10/9 (naime, E/D = (5/4)/(9/8) = A/G = (5/3)/(3/2) = 10/9). Razbijanjem cijelih tonova na polutonove konačno dolazimo do svih točnih intervala u dvanaestonskoj skali:

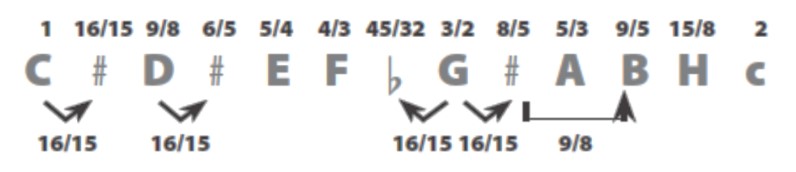
Naime,

C^#=C∙16/15=1∙16/15=16/15                     D^#=D∙16/15=9/8∙16/15=6/5

G^#=G∙16/15=3/2∙16/15=8/5             G^b=G:16/15=3/2:16/15=45/32             B=G^#∙9/8=8/5∙9/8=9/5

Iznosi tako dobivenih polutonova kromatske skale, osim vrijednosti 16/15 = 1.07, imaju još i vrijednosti 25/24 = 1.04, 135/128 = 1.05 i 27/25 = 1.08 (neoznačeni polutonovi imaju iznos 16/15):

Ovi Pitagorini točni intervali dio su tzv. prirodne (ili točne) intonacije pa se za glazbala koja su ugođena na taj način kaže se da su ugođena u prirodnoj (ili točnoj) intonaciji. Osnovni problem prirodne intonacije jest velik broj različitih polutonova, Čak četiri, što često onemogućava vjerne transpozicije. Taj se problem potpuno rješava jednolikom skalom, tj. jednolikim ugađanjem koje preporuča najveći antički muzički teoretičar Aristoksen.

Jednolika skala razdioba je oktave na 12 jednakih polutonova. Ako polutonski interval označimo s p, radi se o sljedećoj razdiobi:

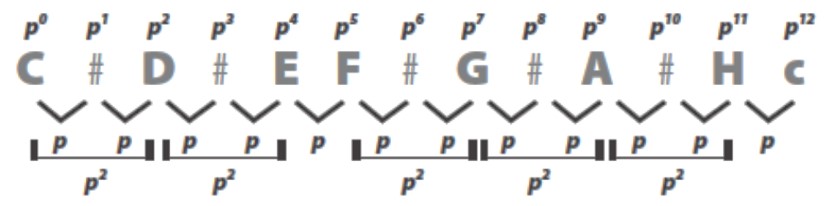
Naravno, p = 2^1/12 ≈ 1.06. Udaljenost tona od tonike češće označavamo eksponentom. Na taj način s multiplikativne skale prelazimo na aditivnu logaritamsku skalu. Dakle s multiplikativne skale (p⁰,p¹,p²,…) prelazimo na aditivnu logaritamsku skalu (0, 1, 2, …). To nam omogućava da intervale zbrajamo, umjesto da ih množimo (npr. to da terca i kvinta čine septimu, u logaritamskoj skali nalazimo zbrajanjem, 4 + 7 = 11, a u osnovnoj množenjem, p⁴∙p⁷  = p¹¹).

Za preciznije određenje intervala uvodi se manja jedinica cent.  On je stoti dio polutona, tj. s = p/100 pa je s = 2^1/1200 ≈ 1.00058. To znači da u logaritamskoj skali izraženoj u centima (tj. u bazi s) vrijedi:

Želimo li neki interval duljine m/n izraziti u centima, moramo zapravo izračunati logaritam od m/n u bazi s:

\(
\Large{\log_{s}\left(\frac{m}{n}\right) = \frac{\log\left(\frac{m}{n}\right)}{\log(s)} = 1200 \cdot \frac{\log\left(\frac{m}{n}\right)}{\log(2)}}
\)

Uz pomoć ove formule točne intervale možemo izraziti u centima i usporediti ih s jednolikima:

Kvarte, kvinte i sekunde gotovo su iste u prirodno intoniranoj i jednolikoj skali (odstupanje do 10 centi nije veliko), ali terce, sekste i septime pokazuju veća odstupanja. Očito je da se radi o bitno različitim ugađanjima “istih” tonova.

Glavna prednost prirodne intonacije, njezina točnost, gubi se pri transponiranju. Usporedite jednoliki pomak iz C u terce E^b i E te u kvintu G, s istim pomacima u prirodnoj intonaciji:

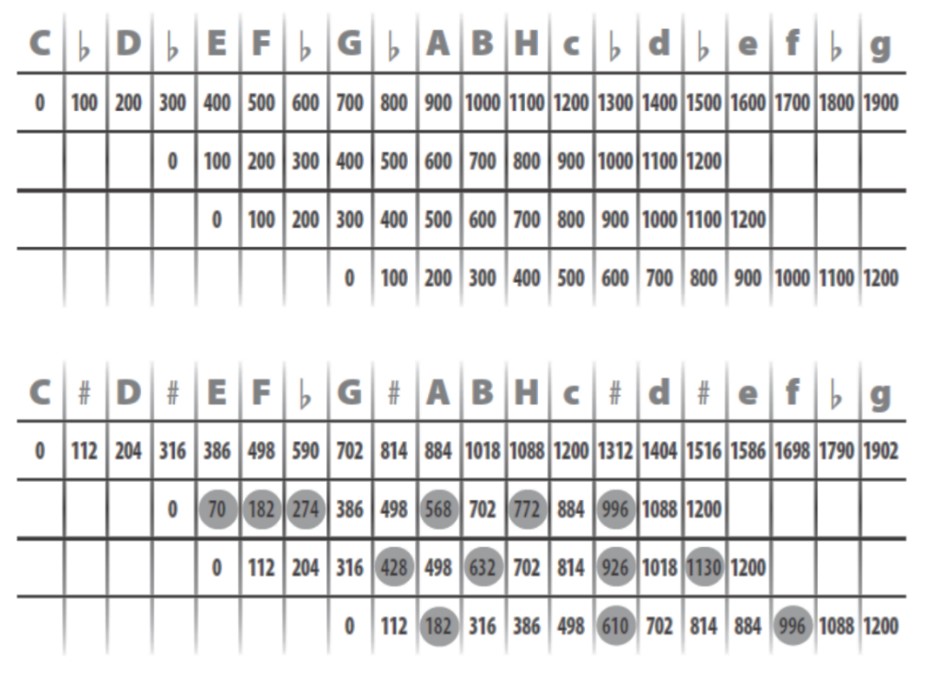
Svi pomaci u jednolikoj skali daju potpuno isti niz polutonova (100, 200, …, 1200), dok pomaci u prirodno intoniranoj skali imaju 3 pogreške u kvintnom pomaku, 4 pogreške u pomaku velike terce i čak 6 pogrešaka u pomaku male terce (pogreške su u tablici zaokružene). Te pogreške nisu male. Od 13 zaokruženih, 7 ih odstupa od točnih vrijednosti za 42 centa, a 6 za 22 centa (“podnošljiva” pogreška je do 10 centa).

Pogreške jednolike razdiobe, koje se ne mijenjaju transponiranjem, iznose od 0 centa do 18 centa, s prosjekom od točno 10 centa.

No, glazbena povijest nije išla putem glazbene teorije. Teorijski je opravdano razmišljati o Ptolemejevim intervalima, ali ih je teško realizirati na konkretnim glazbalima. Tko može točno otpjevati (ili ugoditi) dvije različite velike sekunde 9/8 i 10/9, malu sekundu 16/15 itd. ili 2^1/12, 2^2/12, 2^3/12 itd.

Najlakše je, ipak, otpjevati i prepoznati savršene oktave i kvinte, pa je zato u cijeloj antici i srednjem vijeku standardno ugađanje bilo Pitagorino ugađanje kvintama i oktavama.

• Pitagorino ugađanje

Francuska akademija Notre Dame proglasila je u 13. st. da se do točne skale može doći samo nizom savršenih Pitagorinih kvinti, u kojem je stalni omjer prema prethodnom tonu “božanski” omjer 3:2 (3 za Sveto Trojstvo, 2 za razne dualizme; neba i zemlje, duha i tijela, dobra i zla i sl.).

Krenemo od tona C = 1 kao tona jedinične frekvencije. Kvintu iznad nalazi se G = 3/2. Kvintu iznad G = 3/2 nalazi se d = (3/2)². Taj ton izlazi izvan oktave koja se proteže od C = 1 do c = 2, pa zato d snizimo za oktavu da bismo dobili D = (1/2)(3/2)² = 9/8. Kvintu viši je ton A = (1/2)(3/2)³ = 27/16. Kvintu iznad A je e = (1/2)(3/2)⁴=81/32, koji opet snizimo za oktavu da bismo dobili E = (1/2)²(3/2)⁴ = 81/64. Kvintu iznad E je H = (1/2)²(3/2)⁵ = 243/128. Tako smo dobili sve “bijele” tonove osim F. Spustimo se za kvintu ispod početnog C = 1 i dobit ćemo F’ = 1/(3/2) = 2/3, pa lako možemo naći za oktavu viši F = 2(2/3) = 4/3. Tako smo kvintama i oktavama ugodili sve “bijele” tonove dijatonske skale:

F←C→G→D→A→E→H

Spustimo se od F za dvije kvinte i dobit ćemo (uz odgovarajuće pomake za oktavu više) B = 2²(2/3)² = 16/9 i E^b= 2²(2/3)³ = 32/27. Dignimo se od H za tri kvinte i (uz pomake za oktavu niže) imamo F^# = (1/2)³(3/2)⁶ = 729/512, C^# = (1/2)⁴(3/2)⁷ = 2187/2048 i G^# = (1/2)⁴(3/2)⁸ = 6561/4096. Tako smo ugodili sve tonove kromatske skale:

E^b←B←F←C→G→D→A→E→H→F^#→C^#→G^#

To je tzv. Pitagorino ugađanje kvintama (kvintni krug).

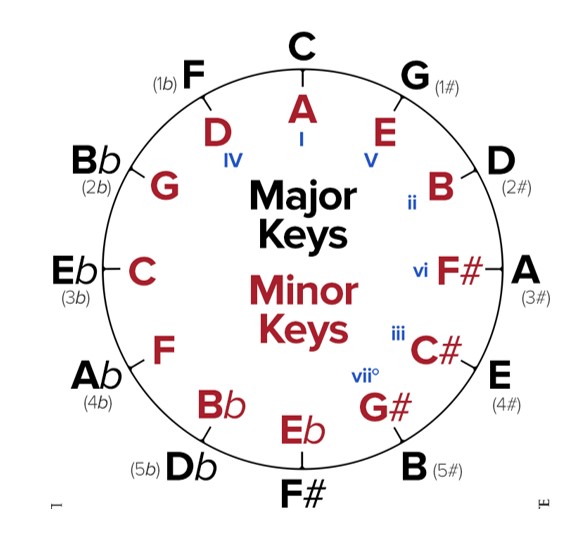
U ovom slučaju to je Pitagorino E^b – G^# ugađanje, jer se od C krećemo do E^b prema dolje i do G^# prema gore. Dobivene vrijednosti možemo iskazati omjerima ili preglednije u logaritamski izračunatim centima (vrijednosti u centima zaokružene su do cjelobrojnih vrijednosti):

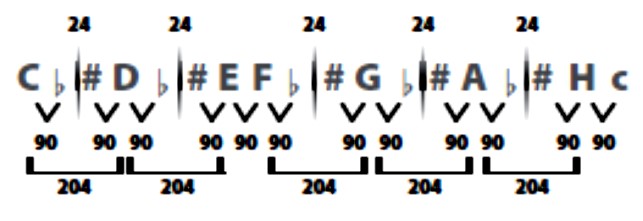
Uočite da polutonovi tako dobivene skale nisu jednaki, oni iznose 114 centa  ili 90 centa. Manji je Pitagorin dijatonski poluton (naime, omjer 256/243 ima 90 centi), dok je veći poznat pod imenom Pitagorin apotom.

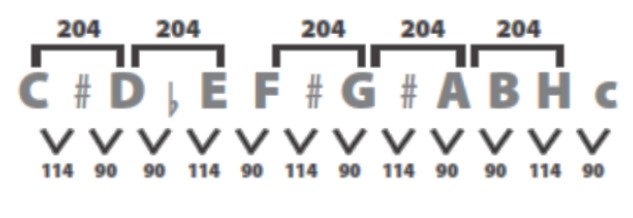
Vidimo da cijeli ton može imati 204 centa ili 180 centa. No, budući da se apotom od 114 centa uvijek pojavljuje između tona X i njegova povišenja X^# ili sniženja X^b, slijedi da svaki cijeli ton dijatonske “bijele” skale ima 204 centa.

Ovo ugađanje ima jedan veliki nedostatak. Sve kvinte koje smo neposredno ugodili sastoje se od 4 dijatonska polutona i 3 apotoma, 4 ∙ 90 + 3 ∙ 114 = 702, i savršene su. Nažalost, kvinta G^# – e^b, koja je krajnji rezultat našeg ugađanja, i koja nije neposredno ugođena, sastoji se od 5 dijatonskih polutonova i 2 apotoma, 5 ∙ 90 + 2 ∙ 114 = 678. Ona ne zvuči dobro i zove se vučji interval, jer zvuči kao vučje zavijanje. Isto vrijedi i za kvartu E^b – G^#, koja je 3 ∙ 114 + 2 ∙ 90 = 522, umjesto savršenih 3 ∙ 90 + 2 ∙ 114 = 498. Svako Pitagorino ugađanje imat će ovakve vučje intervale, koje određuju krajnji tonovi u nizu kvinti, jer 12 kvinti koje prekrivaju raspon od 7 oktava i pritom “pogađaju” sve tonove kromatske skale to ne rade do kraja točno. Naime, 2⁷ < (3/2)¹² pa E^b i G^# ne tvore savršene, nego vučje intervale. Izraženo u centima (oktava ih ima 1200, a savršena kvinta 702):

7 ∙ 1200 < 12 ∙ 702        tj.        7 ∙ 1200 < 12 ∙ 700 + 12 ∙ 2.

To znači da se vučji intervali razlikuju od savršenih za 12 ∙ 2 = 24 centa. Vučja kvarta je za 24 cent prevelika, a vučja kvinta za 24 cent premala. Interval od 24 centa, koji čini te razlike, zove se Pitagorin zarez. (Uočite da je on jednak razlici Pitagorinih polutonova od 114 centa  i 90 centa što nije slučajno. Ta i mnoge druge pravilnosti objašnjene su u [Š2].)

Osim po jedne nesavršene kvinte i kvarte, Pitagorino ugađanje generira i terce, koje su sve nesavršene. Velika terca ovoga ugađanja ima duljinu izraženu omjerom 81/64, što se razlikuje od savršenih 5/4 = 80/64. Interval, za koji se razlikuju te velike terce, ima duljinu izraženu omjerom (81/64)/(80/64) = 81/80, što je 22 centa. Isti interval razdvaja savršenu malu tercu 6/5 od ugođene 32/27, jer je (6/5)/(32/27) = 81/80. Dakle, kvintama ugođena velika terca za 22 centa  je veća od savršene, dok je kvintama ugođena mala terca za 22 centa manja od savršene. Njihov zbroj je savršena kvinta (jer se višak i nedostatak od 22 centa poništavaju), osim na E^b i G^# na kojima su gotovo savršene male terce, ali (zato) jednako loše velike. Interval od 22 centa, za koji se savršene terce razlikuju od kvintama ugođenih, zove se sintonički zarez.

Sintonički zarez karakterističan je za sve terce u Pitagorinom sustavu ugađanja, dok je Pitagorin zarez karakterističan samo za jednu vučju kvintu i samo za jednu vučju kvartu. Zato je Pitagorino ugađanje posebno pogodno za izvođenje glazbe u kojoj su kvarte i kvinte dominantna suzvučja (uz nužno izbjegavanje vučjih E^b i G^#) i u kojem terce čine disonantni element. Takva je gotička polifonija, sa svojim aktivno disonantnim tercama, savršenim kvintama i kvartama, te malim dijatonskim polutonom (od svega 90 centa) za efektne kadence. S druge strane, harmonija trozvuka baziranih na tercama i kvintama, koja se pojavljuje u 15. st. i vlada zapadnom glazbom sve do danas, ne može podnijeti sintonički zarez i njegove loše terce. Zato će se glazbenici od renesanse do romantizma koristiti novim ugađanjima, koja eliminiraju sintonički zarez. Spomenimo još da Pitagorinim G^b – H ugađanjem, koje rabi sljedeći niz kvinti:

G^b ← D^b ← A^b ← E^b ← H^b ← F ← C → G → D → A → E → H,

te F – A^# ugađanjem, koje rabi niz:

F←C→G→D→A→E→H→F^#→C^#→G^#→D^#→A^#,

dobivamo ukupno 17 tonova uz pomoć kojih možemo izvoditi i savršene terce:

Ovakva 17-tonska skala poznata je od 15. st, a postojale su i klavijature koje su je realizirale s dvostrukim crnim tipkama (za izvođenje sniženih tonova b i povišenih #, koji su identični u jednolikoj skali, ali ne i u Pitagorinoj).

• Zašto baš dvanaest polutonova?

Zašto oktava sadrži 12 polutonova? Vidjeli smo da pentatonske, heksatonske i heptatonske skale izabiru svoje tonove iz temeljne dodekatonske raspodjele, ali susreli smo se i s #b-raspodjelom koja ima 17 tonova u oktavi (v. kraj prethodnog poglavlja). Mikrotonski skladatelji 20. st. koriste se skalom s 41 mikrotonom pa i s mnogim drugim brojevima mikrotonova, no prevlast veličanstvenih 12 još je uvijek neupitna.

Ima li kakvih racionalnih razloga kojima bismo mogli objasniti ovu nadmoć dodekatonske raspodjele?

Vidjeli smo kako Pitagorini točni intervali 1:2:3:4:5 vode k dvanaestonskoj raspodjeli oktave, ali mogu dovesti i do sedamnaestonske. Razmislimo zato još jednom kako bismo došli do osnovnog tonskog materijala, polazeći od toga da prednost dajemo Pitagorinim malim omjerima.

Odaberimo prvi ton koji želimo u našoj glazbi i njegovu frekvenciju promatrajmo kao jediničnu. Unatoč Jobimovoj Samba por una nota sô, jedna nota nije dovoljna. U skladu s Pitagorom dodajmo našem jediničnom tonu sve one tonove koji su za određeni broj oktava ispod i iznad njega. U području frekvencija koje čujemo (od 20 Hz do 20 000 Hz) to je najviše 10 oktava:

2^-5←2^-4←2^-3←2^-2←2^-1←1→2¹→2²→2³→2⁴→2⁵

Rijetki su glasovi raspona većeg od dvije oktave pa su im zasad na raspolaganju tri tona, koja osim toga zvuče isto. Zato ćemo, u skladu s Pitagorom i proglasom akademije Notre Dame, našem notnom materijalu dodati kvinte i njima odgovarajuće oktave:

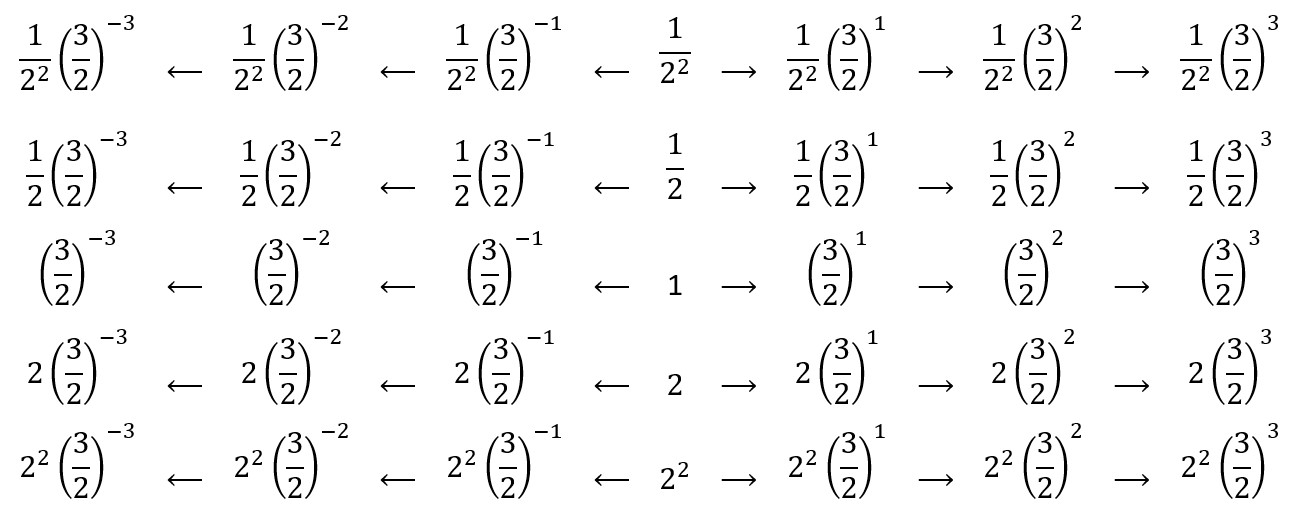
Na taj način dolazimo do beskonačno mnogo tonova, unutar svake oktave, koji su zadani omjerima oblika:

\(
\Large{\frac{1}{2^m} \left(\frac{3}{2}\right)^n} \quad m,n = 0, \pm1, \pm2, \ldots
\)

Za svaki eksponent n imamo po jedan novi ton, koji se pomoću eksponenata m pomiče za m oktava niže ili više. Budući da se nijedan od tih tonova ne poklapa s osnovnim tonom, jer je

\(
\Large{\frac{1}{2^m} \left(\frac{3}{2}\right)^n \neq 1} \quad \text{jer je} \quad 3^n \neq 2^{m+n},
\)

postupak akademije Notre Dame stalno generira nove tonove. Glazba s beskonačno mnogo nota jednako je nemoguća kao i ona sa samo jednom, pa postupak generiranja moramo negdje zaustaviti. Prirodno je stati pri n-tom tonu ako se on, vraćen u osnovnu oktavu, bar približno poklapa s osnovnim tonom (budući da je točno poklapanje nemoguće). Na primjer, za 7. i 12. ton imamo sljedeće aproksimacije:

\(
\Large{\frac{1}{2^4} \left(\frac{3}{2}\right)^7 \approx 1} \quad \text{tj.} \quad \frac{3}{2} \approx 2^{\frac{4}{7}} = 1.486 \quad (686c)
\)

\(
\Large{\frac{1}{2^7} \left(\frac{3}{2}\right)^{12} \approx 1} \quad \text{tj.} \quad \frac{3}{2} \approx 2^{\frac{7}{12}} = 1.498 \quad (700c)
\)

Prva je dosta loša, i zapravo znači poistovjećivanje Pitagorinog tona C^# s osnovnim tonom C, dok je druga bitno bolja i svodi se na Pitagorino poistovjećivanje tonova E^b i D^# (usp. tabelu kvintnih pomaka u prethodnom poglavlju).

U jednolikom ugađanju ove dvije aproksimacije imaju sljedeće značenje. Prva aproksimacija znači da je kvinta u jednolikoj skali sa 7 tonova aproksimirana četvrtim tonom, 2^4/7 = 1.486 ≈ 1.5 = 3/2. Druga aproksimacija znači da je kvinta u jednolikoj skali s 12 polutonova, aproksimirana sedmim polutonom, 2^7/12 = 1.498 ≈ 1.5 = 3/2.

Očito je da 1.498 bolje aproksimira 1.5 nego što to čini 1.486. Nameće se, međutim, pitanje nije li u jednolikoj skali s n tonova kvinta još bolje aproksimirana m-tim tonom za neki drugi broj jednolikih tonova n i neki drugi redni broj kvinte m. Matematički, problem se svodi na izračunavanje razlomka m/n koji što bolje aproksimira broj x zadan zahtjevom:

\(
\Large{\frac{3}{2} = 2^x} \quad \text{tj.} \quad x = \log_{2}\left(\frac{3}{2}\right) = \frac{\log\left(\frac{3}{2}\right)}{\log(2)}
\)

Budući da je x = log (3/2)/log 2 iracionalni broj, ne postoji razlomak m/n takav da je x=m/n. Iracionalni x moguće je samo aproksimirati razlomkom, a teorija verižnih razlomaka pokazuje nam kako se to može učiniti na najbolji način.

Verižni razlomak je razlomak oblika:

\(
\Large{q_0 + \frac{1}{q_1 + \frac{1}{q_2 + \frac{1}{q_3 + \frac{1}{q_4 + \frac{1}{\ddots}}}}}}
\)

gdje su q₀,q₁,q₂,q₃,q₄,…   prirodni brojevi, koje zovemo kvocijentima tog verižnog razlomka, a njega jednostavnije zapisujemo ovako:

[q₀,q₁,q₂,q₃,q₄,…   ].

Ako verižni razlomak ima konačno mnogo kvocijenata q_i onda je on uistinu razlomak, tj. racionalan je broj. Na primjer,

\(
\Large{[0,1,1,2] = 0 + \frac{1}{1 + \frac{1}{1 + \frac{1}{2}}} = \frac{3}{5}}
\)

Ako verižni razlomak ima beskonačno mnogo kvocijenata q_i onda je on iracionalan broj. Vrijedi i obrat. Svaki realni broj može se izraziti u obliku verižnog razlomka, racionalni u konačnom obliku, a iracionalni u beskonačnom. Na primjer,

\(
\Large{ \frac{7}{12} = 0 + \frac{1}{\frac{12}{7}} = 0 + \frac{1}{1 + \frac{5}{7}} = 0 + \frac{1}{1 + \frac{1}{\frac{7}{5}}} = 0 + \frac{1}{1 + \frac{1}{1 + \frac{2}{5}}} = 0 + \frac{1}{1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{2}}}} = [0,1,1,1,2]}
\)

U sljedećem primjeru verižnog razvoja iracionalnog broja \(\small{\sqrt{2}}\) važno je uočiti da je:

\(
\Large{\sqrt{2} – 1 = \frac{(\sqrt{2} – 1)(\sqrt{2} + 1)}{\sqrt{2} + 1} = \frac{1}{\sqrt{2} + 1}}
\)

Naime, tada vidimo da je:

\(
\Large{\sqrt{2} = 1 + (\sqrt{2} – 1) = 1 + \frac{1}{\sqrt{2} + 1} = 1 + \frac{1}{2 + (\sqrt{2} – 1)} = 1 + \frac{1}{2 + \frac{1}{\sqrt{2} + 1}}}
\)

\(
\Large{1 + \frac{1}{2 + \frac{1}{2 + (\sqrt{2} – 1)}} = 1 + \frac{1}{2 + \frac{1}{2 + \frac{1}{\sqrt{2} + 1}}} = [0,1,2,2,\ldots ]}
\)

Ako realni broj x prikažemo u obliku verižnog razlomka(konačnog ili beskonačnog):

x=[q₀,q₁,q₂,q₃,q₄,…   ]

onda su početni komadi tog verižnog razlomka, razlomci

\(
\Large{x_0 = q_0 = \frac{q_0}{1} = \frac{m_0}{n_0}} \quad \Large{x_1 = q_0 + \frac{1}{q_1} = \frac{q_0 q_1 + 1}{q_1} = \frac{m_1}{n_1}}
\)

\(
\Large{x_2 = q_0 + \frac{1}{q_1 + \frac{1}{q_2}} = \frac{q_2(q_0q_1 + 1) + q_0}{q_2q_1 + 1} = \frac{m_2}{n_2} \ldots}
\)

Može se dokazati da su oni najbolje racionalne aproksimacije broja x, uz njihovu veličinu nazivnika (za koji držimo da je do kraja skraćen brojnikom). To znači da neki razlomak m/n bolje aproksimira broj x no što to čini razlomak x_k= m_k/n_k, samo ako je n>n_k. Npr. početni komadi beskonačnog verižnog razlomka \(\small{\sqrt{2}}\)=[1,2,2,2,2,2,…] sljedeći su razlomci:

\(
\Large{[1] = \frac{1}{1}, \quad [1,2] = \frac{3}{2}, \quad [1,2,2] = \frac{7}{5}, \quad [1,2,2,2] = \frac{17}{12}, \quad \text{itd.}}
\)

To preglednije zapisujemo ovako:

Dakle, 7/5 je najbolja aproksimacija od √2 s nazivnikom do 5, a 17/12 je najbolja s nazivnikom do 12. Moguće je da s nazivnikom između 5 i 12 postoji aproksimacija bolja od 7/5 i lošija od 17/12. Ona mora biti između [1, 2, 2] = 7/5 i [1, 2, 2, 2] = 17/12, a iz teorije verižnih razlomaka slijedi da je jedini kandidat za takvu aproksimaciju [1, 2, 2, 1] = 10/7. Budući da je 10/7 lošija aproksimacija od 7/5 (što se lako može provjeriti na računalu), slijedi da je 17/12 prva bolja aproksimacija za \(\small{\sqrt{2}}\) poslije 7/5.

Nešto općenitije, ako npr. između aproksimacije [q₀,q₁,q₂] i [q₀,q₁,q₂,4] postoji neka koja je bolja od prve, ona mora biti oblika

[q₀,q₁,q₂,1],[q₀,q₁,q₂,2]  ili [q₀,q₁,q₂,3].

Ove rezultate o verižnim razlomcima možemo primijeniti na rješavanje našeg problema optimalnog broja tonova u oktavi. Pokazali smo da se on sveo na nalaženje razlomaka koji najbolje aproksimiraju x = log(3/2)/log 2. Taj broj najprije treba izraziti u obliku verižnog razlomka:

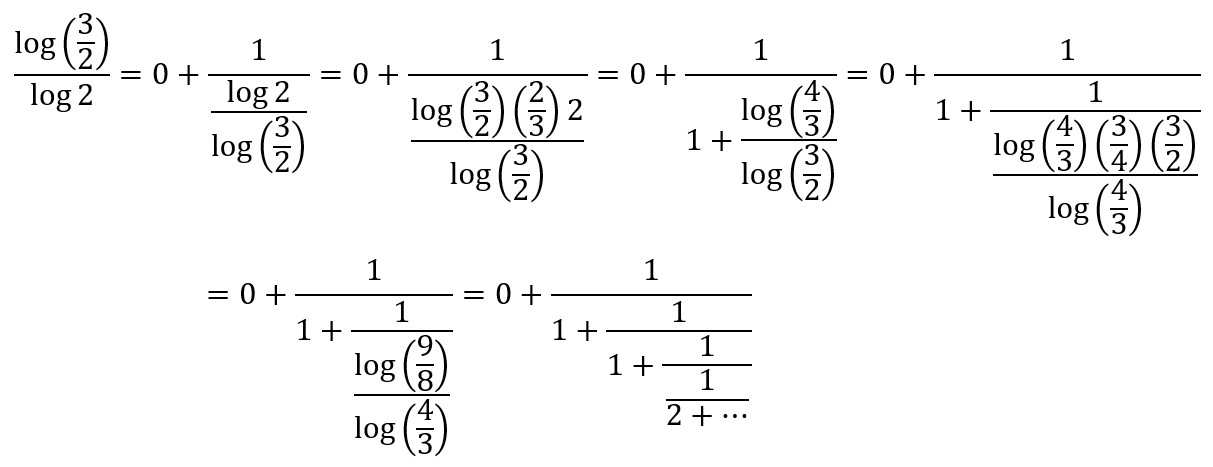
Nastavljajući postupak, dobili bismo:

\(
\Large{\frac{\log\left(\frac{3}{2}\right)}{\log(2)} = [0,1,1,2,2,3,1,5,\ldots]}
\)

Odgovarajuće aproksimacije izgledaju ovako:

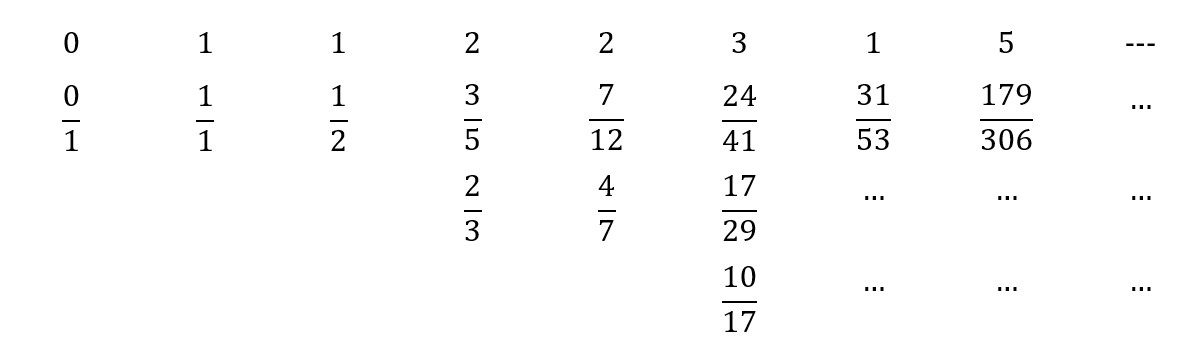
Na računalu se može provjeriti da je 10/17 lošija aproksimacija od 7/12, pa je zato odbacujemo. Dakle, najbolje aproksimacije broja x, do njihove veličine nazivnika, su:

\(
\Large{\frac{2}{3}, \quad \frac{3}{5}, \quad \frac{4}{7}, \quad \frac{7}{12}, \quad \frac{17}{29}, \quad \frac{24}{41}, \quad \frac{31}{53}, \ldots}
\)

Aproksimacija 17/29 znači da oktavu treba podijeliti na 29 mikro tonova, s tim da je 17. ton kvinta. Iznos je te kvinte izvrsnih 2^17/29 = 1 .5013. Nedostatak te podjele (kao i one na 41, 53, … mikro tonova) je to što je 29 mikro tonova u oktavi, za svaku izvedbu osim elektronske, potpuno neprikladno. Kvinta 4/7 (a pogotovo 3/5 i 2/3) bitno je lošija jer je 2^4/7 = 1 .486 = 686 centi, što je 17 centi daleko od savršene kvinte. Kao optimum preostaje nam 12 tonova u oktavi sa 7. tonom kao kvintom. Naime, 2^7/12 = 1 .498 = 700 centi, što je samo 2 centa daleko od savršene kvinte.

Možemo zaključiti da jednolika skala s korektnim kvintama i pristupačnim brojem tonova može imati jedino 12 polutonova. To je teorijski nužni izbor, do kojeg je glazbena praksa došla bez teorije.

Mogli bismo se pitati što je optimalna jednolika skala koja, uz pristupačni broj polutonova, želi korektne kvarte. Problem se matematički svodi na verižne aproksimacije broja:

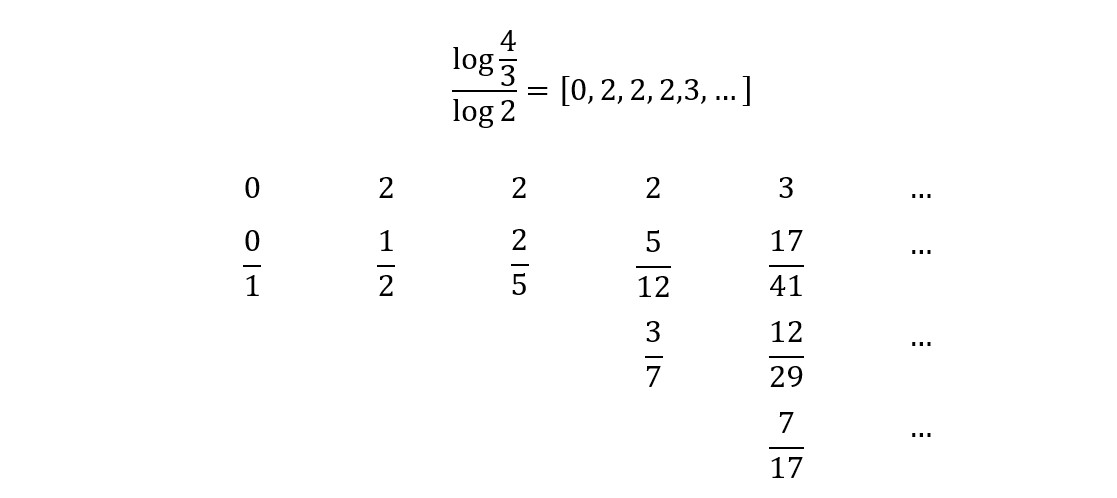
Na računalu se može provjeriti da je 7/17 lošija aproksimacija od 5/12, pa se mora odbaciti. Najbolje aproksimacije, do njihove veličine nazivnika, su:

\(
\Large{\frac{2}{5}, \quad \frac{3}{7}, \quad \frac{5}{12}, \quad \frac{12}{29}, \quad \frac{17}{41}, \ldots}
\)

Odmah vidimo da je 5/12 najbolja aproksimacija, s dostupnim brojem polutonova. Međutim, ovo je ona ista podjela koju smo pronašli za točne kvinte. U njoj je kvarta 5. od 12 polutonova, dok je kvinta 7.

Želimo li korektne terce, dobit ćemo nešto drukčije rezultate. Naime za veliku i malu tercu imamo sljedeće verižne aproksimacije:

Na računalu se može provjeriti da su 6/19, 5/16 i još četiri (neupisana)razlomka u 3. stupcu lijeve tablice lošije aproksimacije od 9/28 pa ih treba odbaciti. Dakle, najbolja podjela oktave za točne velike terce je podjela na 19 polutonova, s velikom tercom kao 6. tonom (moglo bi se razmišljati o 22, 25 ili 28 polutonova, ali oni neće biti povoljni za male terce).

Na računalu se može provjeriti da je 2/7 u desnoj tablici lošija aproksimacija od 5/19 pa se mora odbaciti. Stoga je najbolja podjela oktave za točne male terce podjela na 11, 15 ili 19 polutonova. S obzirom da velike terce preferiraju 19 polutonova, 19-tonska ljestvica je definitivno najbolja ljestvica za terce.

U takvoj bi ljestvici izvrsna mala terca (316 centi) bila 5. poluton, podnošljiva velika terca (379 centi) bila bi 6. poluton, podnošljiva kvinta (695 centi) bila bi 11. poluton, a podnošljiva kvarta (505 centi) bio bi 8. poluton. Takva se ljestvica može realizirati dijeljenjem crnih tipki na dvije i umetanjem jedne nove crne tipke između E i F te H i c.

No, 19 polutonova možda je ipak previše pa 12 veličanstvenih suvereno vlada gotovo svom glazbom (uz iznimku suvremene mikro tonalne glazbe).

• Reference

[Š1] Šikić, Z. Matematika i muzika, HMD, Zagreb 1999.

[Š2] Šikić, Z.  Generalized Pythagorean Comma, CroArtScia2011 – Symmetry: Art&Science, 169 – 174, 2014.