Kako su oni sve to znali? Duboki rudnik antičke matematike

Iz knjige o antičkoj matematici Serafine Cuomo Željko Ivanković izdvaja tri od bezbroj inspirativnih tema: koliko je suvremenih matematičkih pitanja raspravljano s jednakom težinom već prije više tisuća godina, je li matematika ustvari techne, iako je egzemplar teorije, te navodi probleme s političkom i religijskom upotrebom matematike

• Naslovna fotografija: Prenosivi brončani abakus iz 1. stoljeća, alat rimskog pisara, izložen u Arheološkom muzeju u Aosti (Mark Cartwright / CC BY-NC-SA 4.0)

I

Naziv algebra potječe od arapske riječi al-Jabr. Matematičar Muhamad ibn Musa-al-Hvarizmi (Muḥammad ibn Mūsā al-Khwārizmī) objavio je u Bagdadu oko 820. godine studiju al-Kitāb al-Mukhtaṣar fī Ḥisāb al-Jabr wal-Muqābalah, kojom je uspostavio algebru kao zasebnu matematičku disciplinu. Na latinskom je studija naslovljena Liber Algebrae et Almucabola^[i]. No, u knjizi Ancient Mathematics (Serafina Cuomo, Routledge 2001), a i u mnogim drugim izvorima^[ii], kao „utemeljitelj algebre“ (str. 219) navodi se Diofant (Diophantus), grčki matematičar iz 3. stoljeća iz Aleksandrije, čije je glavno djelo Aritmetika.

Utemeljitelji algebre Diophantus i al-Khwārizmī, među kojima je vremenska razlika više od pola milenija (Wikipedia)

Iz suvremene se perspektive matematika u Antici svodi na aritmetiku i geometriju. Aritmetika se bavi odnosima i pravilnostima među brojevima, koji su po sebi svojevrsno poopćenje: broj 3 zajednički je za 3 jabuke, 3 kuće i 3 konja. Kao takvi brojevi su za Platona bili ‘čista forma’. Antički filozofi i matematičari prilično su pomno i uporno istraživali odnose i pravilnosti među brojevima: neparnim, parnim, prostim, složenim (i iracionalnim, koji su ih najviše mučili jer su ‘nesumjerljivi’ s prirodnim brojevima). Pitagorejce je fasciniralo to što za stvaranje zvučne harmonije glazbenik i glazbalo moraju slijediti brojevne omjere.

U algebri su brojevi dalje poopćeni. Algebarski simboli, na primjer slova x, y, z, općenitiji su i od brojeva: banalna algebarska jednakost glasi: (x – y)^2 = x^2 – 2xy + y^2. Diofant bi u Aritmetici uobičajeno sličnu algebarsku jednakost izrazio riječima, a ne simbolima (što ne mijenja bit stvari). U njezinom bi kompliciranom ‘dokazu’ razlikovao brojeve koji su konstantni (kao što je u prethodnoj jednakosti broj 2), od onih koji su ‘nepoznate veličine’, no u osnovi bi kao ‘dokaz’ naveo aritmetički, brojevni primjer, piše Cuomo (str. 219). Uvrstio bi u prethodnu jednostavnu jednakost umjesto x i y brojeve 5 i 3 kao ‘nepoznate veličine’ i pokazao bi da jednakost vrijedi: s lijeve strane (5-3)^2, to jest 2 na kvadrat, što je 4, jednako je desnoj strani 5∙5 – 2∙5∙3 + 3∙3 = 25 – 30 + 9 = 4.

Al-Hvarizmi razvijao je i dokazivao pravila simboličke kalkulacije ‘za svaki x, y, z …’: uvrsti li se u prethodnu jednakost umjesto x i y bilo koji broj – neparni, parni, prosti, složeni… ona uvijek vrijedi i to ne treba dokazivati pojedinačnim primjerima. Stvar je kriterija je li utemeljitelj algebre Diofant ili Muhamad ibn Musa-al-Hvarizmi. Razni oblici poopćavanja i apstrahiranja veliki su dio matematičkih istraživanja i razvoja. Primjer je ponajprije ilustracija važnog sadržaja knjige Ancient Mathematics da se matematika ipak razvija više kumulacijom hipoteza, zaključaka i znanja nego ‘otkrićima’, kako se obično predstavlja, a koja su tek neki posljednji (?) korak. Gotovo je suvišno isticati da je u knjizi dovedena u pitanje standardna (školska) predodžba koja razvoj matematike od najranijeg doba svodi na poučke, teorije i radove slavnih autora: Tales, Pitagora, Euklid, Arhimed … i njihovih nastavljača. Knjiga je zbirka pokušaja, nabadanja, loših formulacija, ispravaka i ‘konačnih’ zaključaka.

U nastavku se prvo predstavljaju autorica Serafina Cuomo te sadržaj i inspirativan  pristup u knjizi Ancient Mathematics. Zatim se navode još neki primjeri i karakteristike antičke matematike koji ne samo što podupiru zaključak o razvojnom kontinuitetu nego ga predstavljaju kao važnu karakteristiku matematike. Potom se nastoji objasniti donekle neobičnu i potencijalno dalekosežnu tezu da je matematika u Antici pripadala u techne, iako se sve od Platona a naročito danas navodi kao egzemplar teorije. Tezom se dakle naglašava danas najčešće zanemareni dio prirode matematike, a sukladna je zaključku o kontinuitetu, budući da je kumulacija znanja jedna od glavnih osobina tehnologije. Napokon se opisuje politička (i donekle religijska) dimenzija antičke matematike.

II

Ime Serafine Cuomo, profesorice na Sveučilištu Durham, uočio sam u zborniku The Cambridge Companion to the Ancient Greek Economy (Cambridge University Press; 2022), u kojem je u poglavlju 26 kritizirala mit o izostanku tehnološkog progresa u Antici[iii]. Uz spomenutu, o antičkoj matematici objavila je i knjige Pappus of Alexandria and the Mathematics of Late Antiquity (Cambridge University Press, 2000) te Technology and Culture in Greek and Roman Antiquity (Cambridge University Press, 2007)[iv].

Serafina Cuomo (Durham University) i naslovnica njezine knjige

Cuomo Ancient Mathematics započinje anegdotom. Godinama prije objave knjige u neobaveznom ju je razgovoru taksist upitao čime se bavi. Odgovorila je da je povjesničarka antičke matematike. Kad su stigli na odredište taksist je izvukao bilježnicu u koju upisuje najčudnija zanimanja kojima se bave njegovi putnici. Serafinu Cuomo uvjeravao je da se sto posto kvalificirala među deset u vrhu. Implikacija je da su i čitatelji njezinih knjiga (a i ovog prikaza) ‘rijetke zvjerke’. Sami biraju je li im to kompliment ili mana; Cuomo se taksistima kasnije predstavljala kao profesorica ili – češće – turistica.

Antička je matematika prikazana u rasponu od oko tisuću godina, otprilike od 6. stoljeća prije nove ere. Knjiga ima osam poglavlja. Neparna poglavlja, 1., 3., 5., i 7. predstavljaju izvore i nalaze (evidence) za sljedeća razdoblja: Rana grčka matematika; Helenistička matematika; Grčko-rimska matematika; Kasna antička matematika. U parnim su poglavljima analizirana neka izdvojena pitanja karakteristična za pojedino razdoblje. Recimo, u drugom poglavlju se raspravlja o političkoj funkciji matematike, u četvrtom o „stvarnom Euklidu“ i „rođenju zajednice matematičara“, u šestom o razlici u tretmanu matematike u Grčkoj i Rimu i o odnosu praktične/primijenjene i teorijske matematike; a u posljednjem, osmom poglavlju, koje nikako ne treba shvatiti kao zaključno, kao sintezu, jer uostalom priča tu i ne prestaje, teme su odnos božanskog i matematike, te problem antičkih prikaza povijesti matematike. No sva se ta pitanja provlače kroz cijelu knjigu.

III

Disciplinarno, Ancient Mathematics je prvenstveno odlična povijesna knjiga, ali je i knjiga za filozofe i matematičare. Cuomo predaje na odsjeku za povijest, doktorirala je filozofiju, no očito je odlično upućena u razvitak matematike, a za što je potrebno i jedno posebno razumijevanje same matematike. Natprosječno je informirana i o tehničkim disciplinama: mehanici, arhitekturi itd. O poznavanju klasičnih jezika i interpretacije da se i ne govori. Radi se dakle o interdisciplinarnom pristupu, koji se unatoč plodnosti često izbjegava, dijelom zbog zahtjevnosti, a i zato što pretpostavlja prethodni ‘terenski’ rad specijalista.

To da Pitagorin poučak vjerojatno nisu formulirali ni Pitagora ni njegova škola (str 31), da se o Euklidovu životu ne zna skoro ništa a Elementi su kolektivni proizvod gotovo u istoj mjeri u kojoj su to Homerove Ilijada i Odiseja (str 126-135), indikativne su zanimljivosti. Cuomo međutim kroz njih i iza njih kopa i prodire duboko u svoju glavnu temu: razvoj, uloga i mjesto matematike u društvima antičkog razdoblja. Obuhvatnost zahvata nužna je posljedica notornog problema s izgubljenim izvorima i neizbježnosti da se informacije rekonstruiraju posredno, s više strana, a ne samo iz spisa koji su uže matematički. Deklarirani je cilj autorice razumjeti i objasniti što su pojmovi matematika i matematičar podrazumijevali u Antici i kakva im je bila društvena pozicija. Ako se istražuje matematika u Antici, onda je primjereno ustanoviti što se tad smatralo matematikom.

Uz osnovni Euklidov tekst dopisivani su na marginama komentari koji su s vremenom inkorporirani (str 126)

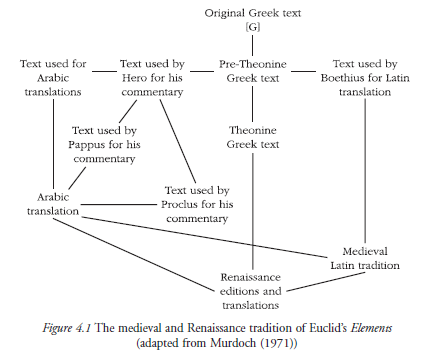
Predodžba o matematici zaista je i bila drukčija nego današnja: matematičarima se nisu nazivali samo oni koji su se bavili ‘čistom’ matematikom, aksiomima, teoremima, dokazima i njihovom sistematizacijom nego i oni koji su se koristili aritmetikom i geometrijom u mjerenju i određivanju granica zemljišta, gradnji, računanju prihoda i zarade, plovidbi, astronomi i graditelji sunčanih satova … Rješavanjem problema s kojima su se suočavali poticali su unapređenje i sudjelovali u razvoju i ‘čiste’ matematike.

IV

Primjera koji sugeriraju kontinuitet razvoja matematike u knjizi je mnogo. U posveti na početku 3. poglavlja, koje je sa šezdesetak od 260 stranica najduže u knjizi, Cuomo citira Arhimedovu raspravu Sand-Reckoner: „Neki brojevi koje sam imenovao … premašuju ne samo broj zrna pijeska koji može ispuniti Zemlju, nego čak i broj zrna pijeska koji može ispuniti sam svemir.“ (str 62) Arhimed je izračunao da se svemir može ispuniti sa 10^24 zrna pijeska, što je – objasnio mi je jedan fizičar – „10^14 kubika a to je kugla promjera 30 km. Skroman svemir. U opažljivom svemiru, čiji je promjer 90 milijardi svjetlosnih godina, samo broj atoma je 10^80”. Poanta je međutim u drugome. Arhimed je Sand-Reckoner pisao Gelonu, kralju Sirakuze običnijim jezikom nego druge radove da mu pokaže kako ga smatra upućenim u matematička pitanja i politički mu se približi (str 140, 141). No, važniji je dio traktata rasprava s Teokritom (Theocritus) koji je razlikovao brojeve koji su ‘točni’, u smislu da su izračunljivi (bez obzira na to koliko su veliki), od brojeva koji su „izvan mogućnosti izračuna“ (str. 75). Rasprava o beskonačnim veličinama kao nečem izdvojenom, različitom od konačnih, bez obzira na to koliko su velike, te o njihovom odnosu,  traje dakle tisućljećima (sve do Hilbertova hotela, i do danas).

U posveti na početku 5. poglavlja Cuomo citira Plinija Starijeg (Naturalis Historia), da su se ‘neki’ usudili istraživati, čak i objaviti, dimenzije svemira, što je puka ludost, da mjeru bilo čega ne može izračunati onaj koji ne zna svoju mjeru (str. 143). Izgleda kao poetski kontraargument Arhimedu (‘daj se ti zbroji’), no možda i nije pretjerano uočiti da je i kod Kanta odnos beskonačno-konačno aporija ljudskog uma. Kao da to kaže i Plinije: razmisli li čovjek o svojim kapacitetima, shvatit će da mu je veličina svemira nespoznatljiva.

U svojoj ‘ludosti’, Arhimed se kao mehaničar i geometričar u istraživanju kretanja bavio i infinitezimalno malim veličinama, svjestan da probleme ne uspijeva riješiti (str 111- 113). Otprilike 19 stoljeća kasnije Leibnitz i Newton standardiziraju operacije s infinitezimalnim veličinama i omogućuju ono utemeljenje mehanike s kojim se Arhimed mučio.

I postojanje svojevrsne community of letters, kakva je prema Joelu Mokyru, povjesničaru tehnologije, omogućila razvoj znanosti, industrije i obogaćivanje Zapada[v],  još je jedan primjer analogije i svojevrsnog kontinuiteta Antike i Novog vijeka. Cuomo na niz mjesta dokumentira da su se filozofi i matematičari međusobno dopisivali (npr. Arhimed s Eratostenom), jedni drugima komentirali i ispravljali radove, diskutirali ih unutar i među školama, uočavali da nedostaju dokazi, sami dokazivali hipoteze ili izvodili alternativne dokaze. Komentari na marginama poslije su nerijetko uvrštavani u ‘original’. To je jedan od razloga zašto je, uz nedostatak biografskih informacija, teško ustanoviti autorstvo Euklidovih djela, posebno Elemenata koji su kao najslavniji i najviše komentirani. Matematika jednostavno nije ni bila niti je danas egzaktna kako se pretpostavlja, ima pogrešaka i ispravaka, ono što se smatra očitim često krije puno nerazjašnjenog[vi].

V

Prema Whiteheadovoj doskočici sva je zapadna filozofija tek bilješka uz Platona. Brojevi i geometrijski oblici prema Platonu pripadaju u pravu, višu realnost formi i pojmova (str 24), gdje su još smještene i ideja dobrog, ideja lijepog itd. Radi se o onome što je nepromjenjivo, vječno i uvijek isto, čime se bavi teorija, koju su hrvatski filozofi svojedobno pompozno opisivali kao – ‘čisti zor’, neokaljan stečenim iskustvom, empirijom. Matematika je egzemplar teorije. Nasuprot teorijskom su razni oblici praktičnog znanja koje se bavi onim što je promjenjivo, što može biti ovako i onako. Tako je to u današnjoj interpretaciji koja teži iz složenih i višeznačnih antičkih rasprava formirati jednoznačne podjele[vii]. Iako je dakle viđenje matematike kao teorije bilo utjecajno kako u Antici tako posebno danas, kroz cijelu knjigu Cuomo dokumentira da se matematika u Antici shvaćala i kao techne, jedna vrsta praktičnog znanja o onome što dakle nije uvijek izvjesno.

S tumačenjem te tvrdnje treba biti oprezan. Cuomo ne piše na način da izvodi definitivne sinteze, nego više podsjeća, upozorava, indicira i potiče na razmišljanje. To mi se ne čini manom nego kvalitetom knjige, no kad je riječ o tvrdnji da je matematika (i) techne, a možda i prije svega techne, postavlja se pitanje što to točno znači? U ovom će se odjeljku, na temelju knjige, pokušati pronaći nekoliko karakteristika matematike i izvesti nekoliko interpretacija po kojima ona pripada u techne.

Od početaka je matematika bila namijenjena primjeni: rekonstrukcije grčkih i rimskih geometarskih pomagala

Matematika se već u Antici primjenjivala u administraciji (obračun poreza) ili u ratu (gradnja katapulta, postavljanje logora), ili u poslovima: gradnji, mjerenju zemljišta (geo-metrija), plovidbi i trgovini. Radi se dakle o primjeni matematike u pojedinim tehnologijama i vještinama, što implicira da se od njih razlikuje: ista se matematika, uostalom, koristi u graditeljstvu i brodogradnji. Slično se danas u tehnologiji koristi teorijsko i pouzdano empirijsko znanstveno znanje (episteme). No sama činjenica da je primjenjiva sugerira da s tehnologijama dijeli neke karakteristike po kojima se shvaćala i nazivala techne.

Riječ je o višeznačnom pojmu: techne je i vještina, ishod ovisi o talentu i vježbi, netko je u izvedbi bolji drugi slabiji, ali u primjeni se kako matematike tako i tehnoloških znanja slijede neke procedure i pravila. Oboje imaju svojevrsni normativni karakter, a to implicira (a) da se zna ne samo koje se procedure primjenjuju nego i zašto; zatim (b) da se pravila i procedure mogu poučavati; te, napokon (c) da se i primjena, a ne samo rezultat, mogu vrednovati. Po tim zajedničkim karakteristikama i matematika je techne. Osim toga, i u matematici kao i u tehnologiji do rezultata se može doći na više načina, različitim procedurama i putevima, dokaz se može izvesti jednostavnije ili elegantnije. Svi inženjeri znaju da rješenja mogu biti šlampava ili ingeniozna. (Cuomo dosta pažnje posvećuje razvoju dokaza, velikoj matematičkoj temi koju ovdje moramo preskočiti.)

Različiti načini pisanja brojeva: kako su njima računali i koliko su mogli izračunati

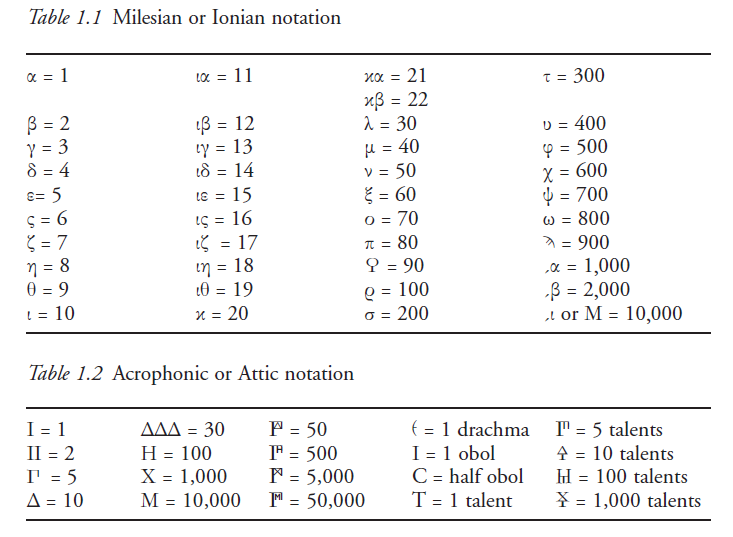
Iako se smatra teorijskom disciplinom (čisti ‘zor’) matematika je oduvijek isprepletena s oruđima. Netko na primjer zbraja ili oduzima ‘na prste’. Danas se služimo arapskim brojevima i učimo kako se njima izvode matematičke operacije. Kako su se izvodile rimskim brojevima, kako su brojevi pisani u Grčkoj? Cuomo je u knjizi objavila Miletsku, Jonsku i Atičku notaciju brojeva. U svakoj su se matematičke operacije izvodile na drukčiji način, neke su bile efikasnije, njima su se određene operacije izvodile lakše, ali nisu bezuvjetno prihvaćane zbog toga što se od navike teško odustaje.

Razvoj ‘računala’, od grčkog, za koji nije jasno kako se točno koristilo, pretpostavlja se da su se oblutci slagali na horizontalne linije, preko rimskog (Wikimedia Commons)

Cuomo piše i o razvoju abacusa (računala) u Grčkoj i kasnije u Rimu. Nekim se abacusima mogu izvoditi samo ograničene operacije, no svi oni slijede i odražavaju neka pravila izračuna koji su i sami tehnologije zato što je procedura primjene pravila tehnologija. Stroj se može prikazati kao shema (danas se onda naziva ‘virtualnim’). U Antici su se za rješenje problema udvostručenja površine kvadra i volumena kocke, zatim za trisekciju kuta i izračun površine kruga istraživali kako instrumenti tako i apstraktne procedure. Matematika je tehnologija. Suvremena računala su procedure, no i ona zapinju, ne samo zbog još premalog kapaciteta za neke matematičke zadatke[viii]. Na rješenje nekih problema čekalo se stoljećima i tisućljećima, za neke još nema rješenja, a za neka rješenja još nije sigurno da su  ispravna. Ishod je izvjestan samo u platonovskoj apstrakciji[ix].  Matematika je techne i po tome što se svodi na procedure-instrumente i o njima ovisi. Sve upućuje na ponovno promišljanje razlike između teorije (znanja o uvijek istom) i prakse kao tehnike, jer izgleda ni u Antici, iz koje je baštinimo, ta podjela nije bila striktna i neupitna.

Ostaci antikythera mehanizma iz Nacionalnog Muzeja u Ateni (Wikipedia) i jedna od rekonstrukcija kako se njime predviđalo kretanje planeta daleko u budućnost

VI

Ovaj prikaz završava političkom ulogom matematike, odnosno ulogom matematike u oblikovanju odnosa unutar zajednice, što čini dobar dio sadržaja knjige. Najkraće, u prirodi je matematike da ‘uvodi red’. Korist od primjene matematike u izmjeri i podjeli zemljišta, određivanju i izračunu poreza na prvi je pogled prilično uvjerljiva, očita. Potkraj prvog stoljeća rimski general Frontinus preuzeo je upravljanje opskrbom vodom u gradu Rimu i zahvaljujući mjerenjima i izračunima na početku i na kraju vodotoka ustanovio ogromne gubitke a zatim i krađe, skretanje i korištenje vode iz akvadukta izgrađenog javnim sredstvima u privatne svrhe (str 169). Na samom početku knjige Cuomo opisuje kopanje tunela sredinom šestog stoljeća prije nove ere, kroz koji se vodom opskrbljivao grad Samos (str. 9). Neočekivana matematička vještina omogućila je da se dvije skupine kopača koji su krenuli svaki sa svoje strane, sretnu na točno izračunatom mjestu na dubini većoj od 1000 metara ispod vrha planine. No stvari se nisu uvijek odvijale tako savršeno. Sredinom drugog stoljeća, dakle sedam stoljeća nakon uspješno prokopanog tunela za Samos, dvije rimske vojne jedinice koje su kopale tunel u sjevernoafričkoj provinciji pokraj alžirskog grada Saladae, nisu se susrele kako je izračun predviđao (str. 158).

Ova dva primjera otvaraju nekolicinu ozbiljnih pitanja, aktualnih i danas. Prvi je problem pogrešivosti, odnosno – kojem ekspertu vjerovati? Ekspert može biti i lopov, ili raditi za jednu stranu, ili nemaran, a ne samo nevješt. Cuomo također piše o institucionalnoj promjeni u rimskim provincijama u Grčkoj. Neslaganja u izračunu veličine zemljišta (i određivanju visine poreza) stanovnici su prije rješavali u međusobnoj raspravi. Nakon rimskog osvajanja odlučujuću su riječ imali geometar iz Rima i carski namjesnik (str. 157). Kao carski izaslanik i inspektor u Bitiniji, na sjeveroistoku Male Azije, Plinije mlađi od cara Trajana traži da mu pošalje geometra jer se od izvođača javnih radova mogu skupiti značajne svote (str. 176). Ali, matematika ne rješava prava pitanja pravednosti: treba li porez određivati prema veličini posjeda, po prihodu ili po glavi.

U pitanju raspodjele i Platon se poziva na matematiku kao odraz prirodnog reda stvari: zauzima se da se u raspodjeli ne slijedi aritmetička jednakost nego ‘geometrijski omjeri’: da više dobije onaj koji je ‘prirodno vrjedniji’ i tako je i u društvu više pozicioniran (str 48, str 199). Danas bi se takva matematika ironično nazvala ‘kreativnom’, no u meritokratskoj ideji o talentu žive neki njezini aspekti. Reakcija na Platonov ‘prirodni poredak’ stiže od liječnika Galena, prema kojem vješt sluga ili rob, čak i dobro trenirani konj, vrijede više nego njihov vlasnik/gospodar (str 209). Ujak Plinija mlađeg, Plinije stariji, eksplicitan je u opisu ograničenja matematičara da dijele pravdu, podsjeća da su ljudske potrebe, pohlepa, vrline i mane, skromnost i arogancija, obiteljski i dobrosusjedski odnosi izvan njihove mogućnosti izračuna:

‘O aristokratskog li umijeća! Vi možete izmjeriti (izračunati) krivulju, svesti svaki oblik na kvadrat, možete reći koliko su udaljene zvijezde, ništa ne izmiče vašoj mjeri: ako ste toliko dobri u vašem umijeću izmjerite čovjekovu dušu, recite koliko je širokogrud ili sitničav. Vi znate što je ispravna linija, ali kakva korist ako ne znate što je ispravan život.“ (str. 178)

VII

Ogromna količina sadržaja knjige Ancient Mathematics Serafine Cuomo u ovom prikazu nije ni spomenuta. Ideja je bila ukazati na kontinuitet, da su današnja pitanja o matematici i pravednosti raspravljana već u Antici, i da u tom pogledu nema nikakvog ‘napretka’, kao i uže matematički problemi kojima su se bavili i bave matematičari u Novom vijeku i suvremenom dobu. Na početku je spomenuta pitagorejska i platonovska fascinacija brojevima koja je kroz tisuću antičkih godina samo mijenjala oblik, ali ne i intenzitet. Augustin, koji je snažno prihvatio kršćanstvo, piše da „broj šest nije savršen zato što je Bog obavio svoj posao u šest dana, nego je Bog obavio svoj posao u šest dana zato što je broj šest savršen“ (str 212). Bog je dakle slijedio matematiku, a ne obratno. Slično je i s modernim shvaćanjem prirode (a često i društva), na primjer u Newtonovu opisu prirode matematičkim principima (Philosophia Naturalis Principia Mathematica). Stvar je samo u tome da se matematičke pravilnosti otkriju, kao Fibonaccijev niz u laticama. Numerologija, proučavanje odnosa među brojevima i njihova ‘ dubljeg značenja’ s jedne je strane mistifikacija: broj 6 je ‘savršen’ (str. 181) jer je u isti mah zbroj (1+2+3=6) i umnožak (1∙2∙3=6) prva tri broja; za pitagorejce bog je ‘iracionalni broj’ (str 76) itd, kao i danas kad se iz brojeva ‘proriče sudbina’, a s druge se strane radi o otkrivanju zakonitosti brojeva.

Završimo ovaj prikaz s radikalnim skeptikom Sekstom Empirikom (Sextus Empiricus) koji negira mogućnost bilo kakvog znanja od etike do matematike. Sekst u geometriji napada definiciju točke (‘znak bez dimenzija’) i linije (‘tijek točaka, dužina bez širine’): kako dakle točka koja je bez dimenzija kreirati liniju koja je dimenzija? A u radu naslovljenom Protiv aritmetičara zaključuje da je broj – ništa! (str 185)

Tako su već u Antici izneseni ne samo početni nego i jaki argumenti za sva današnja shvaćanja prirode matematike: realizam, prema kojem matematika predstavlja jednu zasebnu višu realnost, čije principe treba otkriti u ovoj drugoj stvarnosti, instrumentima (osjetilima) koji su po definiciji ograničeni i nesavršeni; zatim matematički konstruktivizam i logicizam kao i fikcionalističko shvaćanje matematike. Sve bogatstvo sadržaja knjige Serafine Cuomo jednostavno nije moguće iščitati.

• Bilješke

[i] Na engleski je knjiga prevedena pod naslovom: The Compendious Book on Calculation by Completion and Balancing, dostupan na https://legacy-www.math.harvard.edu/~knill/teaching/summer2019/exhibits/algebra/AlgebraMohammedBenMusa.pdf

[ii] Vidi, na primjer, natuknicu Algebra u Enciklopediji Britannica https://www.britannica.com/science/algebra

[iii] Prvi dio mog prikaza zbornika o antičkoj ekonomiji, koji je uredila Sitta von Reden, može se poslušati na poveznici na Trećem programu Hrvatskog radija a drugi će dio prikaza biti emitiran u listopadu 2023.

[iv] Knjiga o tehnologiji u Antici zaslužuje poseban prikaz.

[v] A Culture of Growth, Princeton University Press, 2018

[vi] Dobar putokaz za izučavanje (ne)egzaktnosti matematike knjiga je Joela Hamkinsa Lectures on the Philosophy of Mathematics (koju sam prikazao u članku Matematika i filozofi. Koliko su matematički dokazi zaista egzaktni. Razumljivost)

[vii] Natuknica Episteme and Techne objavljena u Stanford Encyclopedia of Philosophy pregledno prikazuje koliko su se u Antici u različitim pojmovima preklapale karakteristike teorijskog i praktičkog znanja. Za detaljniji studij pojma tehnologije korisne su opsežna Philosophy of Technology and Engineering Sciences (ur Anthonie Meijers, Elsevier, 2009), zatim A Companion to the Philosophy of Technology (ur. Jan Kyrre Berg Olsen, Stig Anddur Pedersen i Vncent F. Hendricks, Wiley-Blackwell 2009) a brži pregled povijesti i mijena pojma tehnologije daju Technology, Critical History of a Concept (Eric Schatzberg, The University of Chicago Press 2018), Technology: A World History (Daniel R. Headrick, Oxford University Press, 2009) i napokon The Oxford Handbook of Engineering and Technology in the Classical World (ur. John Peter Oleson, Oxford University Press 2008)

[viii] Suvremeni problem izračunljivosti raspravlja se u  poglavlju  6. (Computability) u spomenutoj (bilješka vi) knjizi Joela Hamkinsa Lectures on the Philosophy of Mathematics.

[ix] Cuomo se ne bavi neizvjesnošću ishoda koji proistječe iz alternativnih početnih pretpostavki koje su u matematici presudne, kao i uopće u znanstvenoj teoriji. To je u matematici ipak artikulirano u novom dobu. Wittgensteinovo ‘slijeđenje pravila’ zadaje filozofiji istraživanje alternativnih matematika, koje polaze od drukčijih aksioma pa, na primjer, zbroj kutova u trokutu nije uvijek 180 stupnjeva, ali se Einsteinova teorija relativnosti koristi upravo takvom (Riemannovom) geometrijom, a Newtonova Euklidovom. Ta se diskusija može naći u Hamkinsovoj knjizi spomenutoj u bilješci vi, te u knjizi Morality & Mathematics Justina Clarke-Doanea (koju sam prikazao u članku Moral i matematika. Treba li se oko aksioma usuglašavati? Što je realno, a što objektivno). Doduše, Cuomo spominje Protagorinu primjedbu da tangenta u stvarnosti ne dotiče kružnicu samo u jednoj točki kao što tvrde geometričari (str. 42), no to se očito odnosi na odnos stvarnosti i platonovske idealne matematičke apstrakcije.