Klasična vjerojatnost i primjeri povijesnog razvoja

Pojam vjerojatnosti vrlo je složen, to jest razvija se od vrlo očiglednog do zaključivanja koje zahtijeva više koncentracije. Zvonimir Šikić u sedam nastavaka matematički prikazuje pojam vjerojatnosti na način koji se uz nešto volje može slijediti ali uz prikaz daje i zaključke o prirodi vjerojatnosti koji su i zaključci o svijetu

• Naslovna ilustracija: Korespondencijom Pascala i Fermata započeo je razvoj teorije vjerojatnosti (Slika na temelju Wikipedie)

Elementarni uvodi u teoriju vjerojatnosti najčešće se temelje na dva pojma vjerojatnosti, klasičnom  i frekvencijskom. Postoji i treći bejesovski pojam vjerojatnosti, koji vjerojatnost drži „stupnjem plauzibilnosti“ i koji može biti subjektivan ili objektivan. To je najobuhvatniji i najprimjenljiviji, ali i najsloženiji pojam. Počnimo s klasičnim pojmom.

• Slučajni pokus i aksiomi

Za razumijevanje ovoga pojma bitan je pojam slučajnog pokusa (zovemo ga slučajnim zato što je njegov ishod slučajan, a ne zato što je sam pokus slučajan). Na primjer, bacanje igraće kocke smatra se slučajnim pokusom. Svaki mogući ishod bacanja zove se elementarnim događajem (ili ishodom) tog slučajnog pokusa. Skup svih elementarnih događaja slučajnog pokusa zove se prostorom elementarnih događaja i obično se označava s Ω. Dakle, slučajni pokus bacanja igrače kocke ima 6 elementarnih događaja,

Ω = {1, 2, 3, 4, 5, 6}.

Bilo koji skup elementarnih događaja, tj. bilo koji podskup od Ω, predstavlja slučajni događaj. Na primjer, slučajni događaj „bačen je neparan broj“ i slučajni događaj „bačen je broj manji od 5“ predstavljeni su skupovima:

N = {1, 3, 5}       i       M = {1, 2, 3, 4}.

Klasičnu vjerojatnost slučajnih događaja definiramo na sljedeći način (uz konvenciju da broj elemenata u skupu S označavamo k (S)).

Ako slučajni pokus ima konačno mnogo elementarnih događaja i ako iz simetričnosti pokusa možemo zaključiti da su svi oni jednako vjerojatni, onda je vjerojatnost događaja A jednaka  omjeru broja elementarnih događaja u kojima se dogodio A i broja svih mogućih elementarnih događaja – „povoljni kroz mogući“:

Pr (A) = k (A) / k (Ω).

U našem primjeru, Pr (N) = k (N)/k (Ω) = 3/6 = 0.5 i Pr (M) = k (M)/k (Ω) = 4/6 = 0.66666 … .

Jedna je od prednosti klasične definicije to što ona dokaze glavnih svojstava vjerojatnosti čini vrlo jednostavnima. Naime, očito vrijedi:

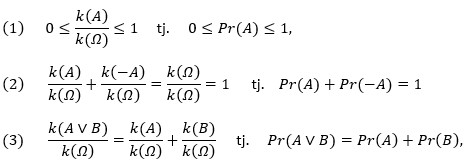
ako se A i B isključuju

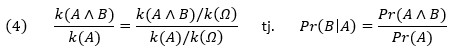
Naravno, (1) – (4) su standardni aksiomi vjerojatnosti. Drugi aksiom zovemo pravilom za vjerojatnost negacije, a treći pravilom za vjerojatnost disjunkcije. Pr (B|A) je vjerojatnost događaja B pod uvjetom da se dogodio A pa četvrti aksiom zovemo aksiomom uvjetne vjerojatnosti. On se češće izriče u obliku koji zovemo pravilom za vjerojatnost konjunkcije:

Ono je općenitije, jer vrijedi i kada je Pr (A) = 0. To nema smisla u klasičnom shvaćanju vjerojatnosti, ali vidjet ćemo da ima smisla u bejesovskom shvaćanju.

Događaji A i B su nezavisni ako je Pr(B│A) = Pr(B), tj. Pr(A∧B) = Pr(A)Pr(B).

Tada je i Pr(A│B) = Pr(A).

• Izvedena svojstva vjerojatnosti

Iz aksioma lako slijede mnoga druga svojstva vjerojatnosti. Na primjer,

odakle odmah slijedi tzv. pravilo totalne vjerojatnosti:

Nadalje, bez zahtjeva da se A i B isključuju imamo poopćeno pravilo za vjerojatnost disjunkcije:

Za propozicije koje se impliciraju ili su ekvivalentne (odnosno skupove koji se sadrže ili su jednaki) imamo

Uobičajeno je A ∧ B kraće zapisati AB. Dakle, pravilo za vjerojatnost konjunkcije zapisujemo Pr(AB) = Pr(A)Pr(B│A).

Iz Pr(HD) = Pr(H)Pr(D│H) = Pr(D)Pr(H│D) slijedi slavni Bayesov teorem:

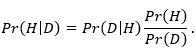
Kad ga primjenjujemo obično o H mislimo kao o hipotezi, a o D kao o podacima (data) koji hipotezu trebaju evaluirati. Imamo li dvije hipoteze H i G koje želimo usporediti u svjetlu podataka D, možemo to učiniti dijeljenjem Bayesovih formula za H i G:

Sve to možete lako sami dokazati ili dokaze možete naći u jednom od nastavaka.

Vjerojatnosti nisu svojstva stvarnosti nego mjere naših znanja o stvarnosti. Thomas Bayes (University of Edinburgh, Bayes Centre)

• Neki jednostavni primjeri

Neobično je koliko se probabilističkih problema može riješiti primjenom jednostavnih aksioma i njihovih trivijalnih posljedica iz prethodnog odjeljka.

1. Problem. Na stolu su, licem na dolje, 4 karte od kojih su 2 bijele i 2 crne. Ako okrenem 2 od te 4 karte, kolika je vjerojatnost da su iste boje?

Rješenje. Ako 4 karte označim s B₁, B₂, C₁, C₂ onda je prostor jednako vjerojatnih ishoda skup svih mogućih parova okrenutih karata:

Ω = {B₁B₂, B₁C₁, B₁C₂, B₂C₁, B₂C₂, C₁C₂}.

Dakle, Pr ({B₁B₂, C₁C₂}) = 2/6 = 1/3.

2. Problem. Jedna je karta bijela s obje strane, jedna je crna s obje strane, a jedna je crno-bijela. Slučajno je odabrana i na stol stavljena jedna od te tri karte. Ako je s vidljive strane crna kolika je vjerojatnost da je i s druge strane crna?

Rješenje. Brzopleti odgovor: s druge strane mora biti crna ili bijela pa je tražena vjerojatnost 1/2.

Međutim, prostor jednako vjerojatnih ishoda za postavljanje karte na stol je {CB, C₁C₂, C₂C₁, B₁B₂, B₂B₁}, gdje prvo slovo označava vidljivu stranu. Mi vidimo crnu stranu pa je prostor jednako vjerojatnih ishoda u našem problemu sužen na

Ω = {CB, C₁C₂, C₂C₁}

Dakle, Pr ({C₁C₂, C₂C₁}) = 2/3.

(Brzopleti odgovor je netočan jer ne uzima u obzir da su u igri i jednobojne karte.)

3. Problem. Neka je p vjerojatnost da u podijeljenim kartama uz dobivenog asa imate još jednog asa, a q neka je vjerojatnost da u podijeljenim kartama uz dobivenog tref asa imate još jednog asa. Je li p = q?

Rješenje. Brzopleti odgovor: da p = q, jer to da je vaš as tref ili neki drugi ništa ne znači za procjenu tih vjerojatnosti.

Međutim, promotrimo jednostavni slučaj špila s dva asa, tref A_t i pik A_p, i dvije dvojke, tref 2_t i pik 2_p, iz kojeg dijelimo po dvije karte. Prostor jednako vjerojatnih ishoda čine mogući podijeljeni parovi karata, {A_t A_p, A_t 2_p, A_t 2_t, A_p 2_t, A_p 2_p, 2_t 2_p}. Ako sigurno imate asa prostor se suzuje na

Ω_p= {A_t A_p, A_t 2_p, A_t 2_t, A_p 2_t, A_p 2_p}    i    p = Pr ({ A_t A_p}) = 1/5.

Ako sigurno imate tref asa prostor se sužava na

Ω_q= {A_t A_p, A_t 2_p, A_t 2_t}    i   q = Pr ({ A_t A_p}) = 1/3.

Dakle, p ≠ q.

Često automatski podrazumijevamo informacije koje zapravo nemamo. To je posebno uobičajeno u situacijama u kojima sa zadanim informacijama problem ne možemo riješiti. Za one koje to zanima malo detaljnije, evo jednog složenijeg problema.

4. Problem. Bacam dvije kovanice. Medu (5 kuna) i slavuja (1 kunu). Vi ne vidite rezultat bacanja, ali vas istinito informiram da je rezultat bacanja mede glava. Kolika je vjerojatnost da je i rezultat bacanja slavuja glava?

Rješenje. Brzopleti odgovor: 1/2, jer rezultat bacanja slavuja ne ovisi o rezultatu bacanja mede.

No, iako rezultat bacanja slavuja ne ovisi o rezultatu bacanja mede, iz toga nužno ne slijedi da rezultat bacanja slavuja ne ovisi o informaciji koju sam vam dao. To će biti tako samo ako pretpostavljate da je moja istinita informacija da je bacanje mede dalo glavu ekvivalentna tome da ste vi to sami vidjeli. Ali možda ja postupam na sljedeći način:

1) Ako je pala jedna glava istinito vam kažem koja je kovanica dala glavu.

2) Ako su pale dvije glave, slučajno odaberem jednu i istinito vam kažem da je ta dala glavu.

3) Ako nije pala nijedna glava, istinito vam kažem upravo to.

U tom slučaju, točan je odgovor na postavljeni problem 1/3. Naime, vjerojatnost da je slavuj dao glavu (Sg) pod uvjetom da ste, prema upravo opisanom postupku, istinito informirani da je medo dao glavu (JMg) je:

Pr (Sg JMg) = Pr (Sg & JMg) / Pr (JMg) =

1/2 Pr (Mg & Sg) / (Pr (Mg & -Sg) + 1/2 Pr (Mg & Sg)) = (1/2) (1/4) / (1/4 + 1/8) = 1/3,

gdje je je 1/2 vjerojatnost da sam između dvije glave (slučaj 2) izabrao medinu.

Bejesovci razumiju da se tu radi o tome da vjerojatnosti nisu svojstva stvarnosti nego su mjere naših znanja o stvarnosti (o čemu više u jednom od nastavaka).

Uočite da u prethodnom problemu nismo konstruirali prostor mogućih ishoda pa zatim metodom povoljni/mogući našli tražene vjerojatnosti, nego smo ih izračunali pomoću aksioma vjerojatnosti i iz njih izvedenih pravila. To mnogi smatraju korektnim „ jer su aksiomi i izvedena pravila posljedice klasične definicije povoljni/mogući pa ih zato možemo slobodno koristiti “. No, to da klasični pojam vjerojatnosti implicira aksiome vjerojatnosti ne znači da aksiomi vjerojatnosti impliciraju klasični pojam. U načelu je moguće da ne postoje slučajni pokusi s jednako vjerojatnim ishodima koji bi korektno opisivali probleme koje možemo riješiti koristeći se aksiomima vjerojatnosti. Ako takvi problemi postoje onda nam klasični pojam vjerojatnosti nije dovoljan, nego nam treba neki općenitiji pojam koji zadovoljava iste aksiome i pomoću kojeg su ti problemi opisivi.

• Stablo vjerojatnosti i Bayesova formula

Nekada vjerojatnosti ishoda slučajnog pokusa možemo odrediti kada one i nisu međusobno jednake. Na primjer, ako pokus možemo razdijeliti u više faza čije su nam vjerojatnosti ishoda poznate. Takav pokus predstavljamo stablom vjerojatnosti. Ono se iz „korijena“  grana prema ishodima prve faze i te grane obilježavamo njihovim vjerojatnostima. Zatim se svaki ishod prve faze grana prema ishodima druge faze, a njegove grane obilježavamo vjerojatnostima ishoda druge faze, pod uvjetom da se desio odgovarajući ishod prve faze. I tako dalje.

Konačni ishod tog pokusa je niz „faznih“ ishoda na odgovarajućoj grani, „od korijena do njenog lista“, a vjerojatnost mu je umnožak svih vjerojatnosti na toj grani. Na primjer, ako pokus u prvoj fazi daje A ili B s vjerojatnostima p i q, a u drugoj fazi C ili D s vjerojatnostima r i s ako se prethodno desio A, odnosno t i u ako se prethodno desio B, stablo vjerojatnosti izgleda ovako:

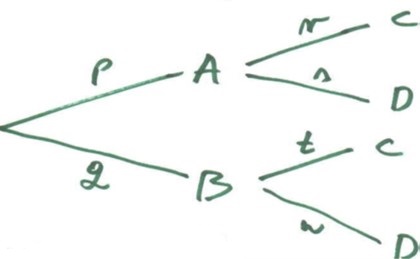
Da su vjerojatnosti konačnih ishoda „umnošci po njihovim granama“ slijedi iz pravila za vjerojatnost konjunkcije:

Pr (AC) = Pr (A) Pr (C A)  = p·r          Pr (AD) = Pr (A) Pr (D A)  = p·s

Pr (BC) = Pr (B) Pr (C B)  =q·t           Pr (BD) = Pr (B) Pr (D B)  = q·u

Prostor mogućih ishoda je Ω = {AC, AD, BC, BD}, a te ishode na stablu vidimo kao 4 odgovarajuće grane „od korijena do lista“.

Kako se koristimo stablom vjerojatnosti najbolje ćemo ilustrirati na konkretnim problemima.

5. Problem. U kutiji je jedna kugla, crna ili bijela s vjerojatnošću 1/2. Dodate u kutiju jednu bijelu kuglu i zatim nasumce izvučete jednu od dvije kugle i vidite da je ona bijela. Kolika je vjerojatnost da je u kutiji početno bila bijela kugla?

Rješenje. Brzopleti odgovor: Na početku je vjerojatnost bijele kugle bila 1/2, vi ste dodali i izvadili bijelu kuglu, tj. ništa niste promijenili, pa je vjerojatnost bijele kugle i dalje 1/2.

Budimo malo precizniji. U prvoj fazi bijeloj kugla B¹ ili crnoj C¹ dodate bijelu kuglu B_d. U drugoj fazi iz kutije u kojoj su sada B¹ B_d ili C¹ B_d vadite jednu kuglu. Dakle, stablo vjerojatnosti je:

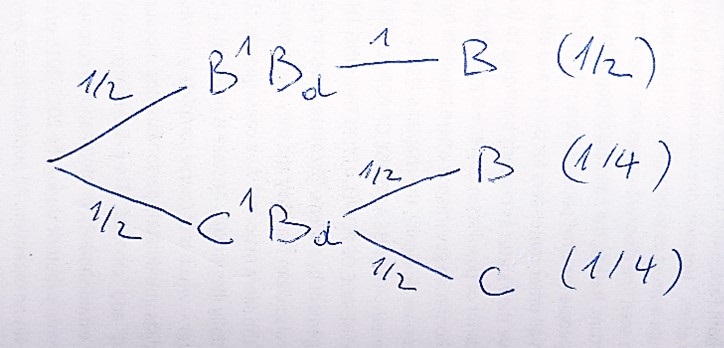
Vjerojatnost da ste na kraju izvukli bijelu kuglu B je ½ + ¼ , a vjerojatnost da je ona iz B¹ B_d je ½ pa je tražena vjerojatnost (½) / (½ + ¼) = 2/3.

Mogli smo upotrijebiti i Bayesovu formulu:

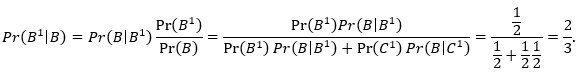
Naravno, dobili smo isti rezultat, ali većina ljudi mnogo lakše rezonira sa stablom vjerojatnosti nego s Bayesovom formulom. (Mogli smo konstruirati i odgovarajući prostor jednako vjerojatnih ishoda pa primijeniti metodu „povoljni/mogući“, ali to bi bilo još složenije. Pokušajte sami.) To dobro ilustrira i sljedeći problem.

6. Problem pozitivnog testa. Izbila je epidemija nove bolesti koja prema podacima iz Kine zahvaća 1% stanovništva. Razvijen je test za tu bolest čija je senzitivnost 90%, tj. vjerojatnost da zaražena osoba bude pozitivna je 90%. Specifičnost toga testa, tj. vjerojatnost da nezaražena osoba bude negativna, također je 90%. Vaš test je pozitivan. Trebate li se zabrinuti?

Rješenje. Brzopleti odgovor „pouzdanost testa je 90% pa su šanse da ste zaražen 90%“ daleko je od istine.

Nacrtajmo odgovarajuće stablo vjerojatnosti u kojem je Ζ = zaražen, a Ζ¯ = nezaražen i izračunajmo Pr(Z│+), tj. vjerojatnost da ste zaraženi pod uvjetom da ste pozitivni.

Sa stabla odmah iščitavamo:

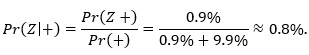
(Brzopleti je odgovor pobrkao Pr(Ζ│+) ≈ 0.8% i Pr(+│Ζ) = 90%.)

Doslovnom primjenom Bayesove formule dobili bismo isti, ali mnogima (u ovom obliku) teško shvatljiv rezultat:

Zašto je gubio? Chevalier de Méré (Esplik)

• Tri povijesna problema vjerojatnosti

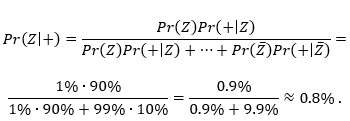
Teorija vjerojatnosti nastala je rješavanjem konkretnih problema pa ćemo je i prikazati kroz te probleme.

De Méréov paradoks

Antoine Gombaud je junaka koji u njegovim esejima zastupa autorove stavove nazivao Chevalier de Méré pa su i njega počeli zvati tim imenom (iako nije bio plemić). Razmišljajući o slučajnom pokusu bacanja kocke zaključio je da je vjerojatnost jedne šestice u 4 bacanja 4 (1/6) = 2/3, jer je vjerojatnost šestice u jednom bacanju 1/6. Po analogiji je zaključio da je vjerojatnost dvije šestice u 24 bacanja 24 (1/36) = 2/3, jer je vjerojatnost dvije šestice u jednom bacanju 1/36. Međutim, kada se počeo kladiti na dvije šestice u 24 bacanja sustavno je gubio, iako je u klađenju na jednu šesticu u 4 bacanja dobivao. Ne uspijevajući objasniti gubitke u jednom i dobitke u drugom slučaju pisao je 1654. godine Blaiseu Pascalu (jednom od najvećih mislilaca tog vremena) tražeći objašnjenje. Pascal je s problemom, koji je nazvao de Méréov paradoks, upoznao Pierrea Fermata i tako je počela slavna korespondencija iz koje je rođena teorija vjerojatnosti.

Pascal je paradoks riješio izračunavši točno najmanji broj bacanja jedne odnosno dvije kocke, u kojem će vjerojatnost bar jedne odnosno dvije šestice biti veća od 50%.

Vjerojatnost da se u n bacanja ne pojavi ni jedna šestica je (5/6) ⁿ pa je vjerojatnost da se pojavi bar jedna 1 – (5/6) ⁿ . Za n = 4 to je 0.52,. Dakle, klađenje na šesticu u 4 bacanja je dobitno. Za manje od 4 bacanja nije dobitno, što vidimo u donjoj tablici koja uspoređuje de Méréov netočni izračun s Pascalovim točnim.

q = 5/6	n=1	n=2	n=3	n=4
de Méré (1-q) n	1/6 = 0.167	1/3 = 0.333	1/2 = 0.5	2/3 = 0.667
Pascal 1-qn	0.167	0.306	0.421	0.518

Vjerojatnost da se u n bacanja ne pojavi ni jedan par šestica je (35/36) ⁿ pa je vjerojatnost da se pojavi bar jedan par šestica 1 – (5/6) ⁿ. Za n = 25 to je 0.51. Dakle, klađenje na šesticu u 25 bacanja je dobitno. Za manje od 25 bacanja nije dobitno, što vidimo u doljnjoj tablici koja uspoređuje de Méréov netočni izračun s Pascalovim točnim.

q = 35/36	n=1	n=12	n=18	n=24
de Méré (1-q) n	1/36 = 0.028	1/3 = 0.333	1/2 = 0.5	2/3 = 0.667
Pascal 1-qn	0.028	0.287	0.398	0.491

Točne brojke u posljednjim stupcima jasno pokazuju zašto je de Méré dobivao u prvoj igri, a gubio u drugoj. Pokazuju i koliko je rubna bila cijela situacija. Da je druga igra igrana sa samo jednim bacanjem više (za n=25, 1-qⁿ = 0,506) de Méré bi dobivao u obje igre, ne bi bilo „paradoksa“ koji traži objašnjenje, a genijalni umovi Pascala i Fermata možda se nikada ne bi posvetili utemeljenju teorije vjerojatnosti.

Luca Pacioli (Famous Mathematicians)

Problem prekinute igre

Prvi značajniji rad u matematici vjerojatnosti koristio se klasičnim pojmom i nalazimo ga u već spomenutoj prepisci Fermata i Pascala iz 1654. Ona je pokazala kako se naizgled složeni problemi mogu svesti na jednostavne izračune s jednako vjerojatnim elementarnim događajima, ali i da nije uvijek jednostavno odrediti prostor takvih događaja (u što smo se već uvjerili). Jedan od problema iz njihove prepiske je slavni problem bodova koji je objavio Luca Pacioli 1494.

Dva igrača igraju niz igara, na primjer bacaju kovanicu i prvi se kladi na glavu, a drugi na pismo. Tko pobijedi u pojedinoj rundi dobiva bod, a prvi koji dosegne određeni broj bodova pobjeđuje u igri i uzima uloge. Odigrali su određen broj rundi i igra je zbog nečega prekinuta. Što je pravedna podjela uloga ako se igra ne može nastaviti?

Problem bodova zbunjivao je mnoge koji su se njime bavili prije Pascala i Fermata. Pacioli je razmatrao igru koja završava kada jedan igrač osvoji 6 bodova, ali je prekinuta kada je prvi igrač osvojio 5, a drugi 3 boda. Smatrao je da je pravedna podjela proporcionalna osvojenim bodovima. Dakle, 5 prema 3. No, kako je 50 godina kasnije primijetio Nicolo Tartaglia, ako se igra prekine nakon prve runde, prema Paciolijevom pravilu igrač koji je dobio tu rundu treba dobiti cijeli ulog, a to nema smisla. Tartaglia je pokušao modificirati Paciolijevo pravilo, ali je na kraju zaključio da definitivan odgovor nije moguć. Čini se da je problem  zbunjivao sve koji su o njemu razmišljali, do ključnog uvida koji je imao Fermat.

Pretpostavimo da nakon prekida jednom igraču do pobjede nedostaje r bodova, a drugome s. To znači da bi se igra odlučila u sljedećih r + s – 1 rundi.  Svi nizovi od r + s – 1 bacanja kovanica predstavljaju jednako vjerojatne elementarne događaje pa vjerojatnosti pobjede jednog i drugog igrača možemo izračunati kao klasične vjerojatnosti.

Za Paciolijev problem, u kojem za pobjedu treba 6 bodova, a nakon prekida prvi igrač ima 5 bodova, a drugi 3, igra bi se odlučila u sljedeće 3 runde. Postoji 8 jednako vjerojatnih nizova glava i pisama u te 3 runde pa je prostor mogućih „završetaka“:

Ω = {GGG, GGP, GPG, PGG, GPP, PGP, PPG, PPP}.

Prvi igrač pobjeđuje u prvih sedam slučajeva , a drugi samo u zadnjem. Omjer vjerojatnosti njihovih pobjeda je 7:1 pa Fermat smatra da pravedna podjela dobitka treba biti u tom omjeru. Dakle, on kao pravedni iznos implicitno koristi očekivanu vrijednost E, koja je vjerojatnostima ponderirani iznos mogućih dobitaka (koji su ulog U ili ništa):

E (prvi igrač) = 7/8 × U + 1/8 × 0          E (drugi igrač) = 1/8 × U + 7/8 × 0

Tako je Fermat klasičnom metodom povoljni/mogući riješio Paciolijev problem. Ali ako imamo veliki broj jednako vjerojatnih slučajeva prebrajanje „povoljnih“ i „mogućih“ postaje glomazno. Razmotrite Tartaglin primjer. Šest bodova je potrebno za pobjedu, a nakon prekida prvi igrač ima jedan, a drugi nijedan bod. Da bi igra završila trebalo bi odigrati još 10 rundi. Dakle, trebamo analizirati 2¹⁰ = 1024 jednako vjerojatnih nizova glava i pisama. Dosta posla da ih sve ispišemo i prebrojimo povoljne za prvog i drugog igrača. Pascal je 1665. objavio bolji način brojanja. Za zainteresirane slijedi objašnjenje kako je Pascal brojao pomoću svog slavnog „trokuta“.

Za prebrojavanje slučajeva u kojima pobjeđuje prvi igrač, Pascal je zbrojio: broj slučajeva u kojima prvi igrač ima 5 pobjeda u 10 pokušaja + broj slučajeva u kojima ima 6 pobjeda u 10 pokušaja + · · · + broj slučajeva u kojima ima 10 pobjeda u 10 pokušaja. Ovi brojevi se nalaze u 10. redu Pascalovog aritmetičkog trokuta (ili Tartaglinog trokuta, ili trokuta Omara Hajjama, svi su oni znali za taj trokut):

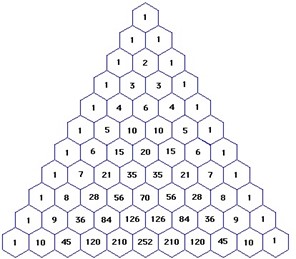
itd.

U N-tom red toga trokuta nalaze se brojevi načina na koje možemo iz skupa od N stvari odabrati njih 0, 1, 2, 3, … , N. Dakle, brojevi za Tartaglin problem nalaze se u 10. redu od 5. mjesta na dalje, tj. to su brojevi 252, 210, 120, 45, 10 i 1. Njihov je zbroj 638 pa je vjerojatnost pobjede prvog igrača 638/1024 (oko 63%). On treba dobiti 63% uloga, a drugi igrač 37%. Pascal, u svojoj knjizi iz 1665, a njegovi prethodnici još ranije, dokazali su da se trokut jednostavno konstruira, jer su sve vrijednosti „uokvirene 1-cama“ zbroj dviju vrijednosti iznad njih.

Problem rođendana

Problem rođendana objavio je Richard Mises 1939. Smislio ga je Harold Davenport oko 1927. Pitanje je kolika je vjerojatnost da najmanje dvije osobe u skupini od N osoba imaju isti rođendan (zanemarujući prijestupne godine i pretpostavljajući da su datumi rođenja jednako vjerojatni, a rođendani pojedinaca neovisni). Ako još niste vidjeli rješenje toga problema, rezultat je iznenađujući.

Najprije izračunajmo vjerojatnost da sve osobe imaju međusobno različite rođendane. Rođendan prve od N osoba može biti bilo koji od 365 dana. Drugi mora biti različit, pa zato može biti bilo koji od preostala 364 dana. Treći može biti bilo koji od preostala 363 dana, itd. do preostalih 365 – (N – 1) dana. Dakle, ukupni broj načina na koji se mogu realizirati rođendani N osoba, tako da svi budu međusobno različiti, je

365 × 364 × 363 × 362× … × (365-N+1).

S druge strane, ukupni broj načina na koji se mogu realizirati svi mogući rođendani N osoba je

365 × 365 × 365 × 365×  … × 365 = 365^N.

Dakle, vjerojatnost da svi rođendani budu međusobno različiti iznosi

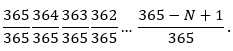
Istu smo vjerojatnost mogli izračunati i pomoću pravila za vjerojatnost konjunkcije (C_j je propozicija „Čovjek s rednim brojem j ima rođendan različit od svih s rednim brojem i < j “):

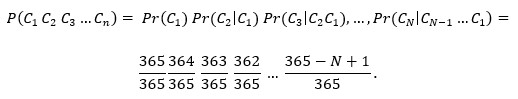
Komplementarna vjerojatnost,

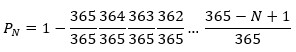
je vjerojatnost da u skupini od  N  osoba postoji bar jedna podudarnost rođendana. U sljedećoj tablici izračunati su iznosi te vjerojatnosti P_N za neke vrijednosti N.

N	5	10	20	23	30	40	60
PN	0.027	0.117	0.411	0.507	0.706	0.891	0.994

Vidimo da je vjerojatnost bar dva podudarna rođendana veća od 50% već u skupini od 23 osobe, a u skupini od 60 osoba skoro je sigurna.

Postoji mnogo varijacija na ovu temu i najčešće se koriste za analizu iznenađujućih koincidencija. Na primjer, moguće je na sličan način dokazati da je velika vjerojatnost da u Hrvatskoj postoje dvije osobe koje imaju isti rođendan, čiji očevi imaju isti rođendan, a i očevi njihovih očeva imaju isti rođendan.

U raspravi o vjerojatnosti pojavio se demon. Pierre-Simon Laplace (Wikipedia)

• Klasična vjerojatnost i determinizam

Problem s klasičnom vjerojatnošću je da vjerojatnost često želimo primijeniti i u situacijama u kojima ne možemo osmisliti slučajni pokus koji bi opisivao tu situaciju i koji bi imao odgovarajuće simetrije iz kojih bismo mogli zaključiti da su svi njegovi elementarni događaji jednako vjerojatni. Ta je simetrija najčešće prisutna u igrama na sreću i sličnim artificijelnim situacijama, a i tada može biti upitna. U mnogim od prethodnih primjera tražene smo vjerojatnosti izveli iz aksioma vjerojatnosti bez da smo našli primjereni slučajni pokus i njegove „moguće“ i „povoljne“. Kao što smo već primijetili, moguće je da ne postoje slučajni pokusi s jednako vjerojatnim ishodima koji bi korektno opisivali probleme koje možemo riješiti koristeći se aksiomima vjerojatnosti.

Štoviše, novovjeki determinizam (ovjekovječen u liku Laplaceovog demona iz 1814.) dovodi u pitanje sam pojam slučajnog pokusa. Razmislite o bacanju kovanice. Palac udara u kovanicu, ona leti, vrti se i konačno  pada na tlo. Isti slučajni pokus u istim uvjetima trebao bi rezultirati s jednim od dva jednako vjerojatna slučajna ishoda, glavom ili pismom. No, ako palac udari kovanicu na isto mjesto istom snagom, ona će letjeti na isti način i sletjeti na istu stranu. Bacanje novčića je deterministički, a ne slučajni pokus. Za zadanu početnu brzinu v i kutnu brzinu ishod možemo izračunati i rezultat je sljedeći – početni uvjeti koji rezultiraju glavom su šrafirani, a oni koji rezultiraju pismom su bijeli.

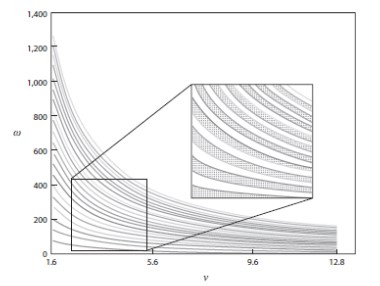
Stroj koji izbacuje kovanicu raznim brzinama v i ω, to i eksperimentalno dokazuje. Kovanica uvijek pada na istu stranu za isti v i ω. Mnogi mađioničari i kockari imaju tu ‘strojnu’ sposobnost, tj. mogu postići da kovanica sleti na koju god žele stranu.

Kako je onda bacanja kovanice postalo paradigmatskim primjerom slučajnog pokusa? Odgovor je pred više od sto godina dao Poincaré 1892. Ako je kovanica bačena snažno, s dovoljno velikom vertikalnom brzinom v i kutnom brzinom ω, osjetljivost na početne uvjete v i ω bit će velika (tj. šrafirani i bijeli dijelovi gornjeg grafa, u tom području, postaju nerazlučivi). Tada čak i vrlo mala promjena početnih uvjeta dovodi do promjene ishoda pa jednaka vjerojatnost ishoda i nije tako loša pretpostavka. Uočite, međutim, da to objašnjenje vjerojatnost vidi kao rezultat našeg nepoznavanja početnih uvjeta bacanja kovanice, a ne kao neko objektivno svojstvo stvarnog bacanja.