Maryam Mirzakhani, žena koja je matematici prilazila neustrašivo

Fieldsovu medalju, najviše matematičko priznanje koje se dodjeljuje svake četiri godine, dobila je 2014. za svoje rezultate u geometriji i dinamici zakrivljenih površina s mogućim primjenama u kriptografiji i teorijskoj fizici, poglavito u istraživanju porijekla svemira i kvantnoj teoriji polja. Bila je jedan od najvećih umova našeg vremena i prema jednoglasnim svjedočenjima kolega i prijatelja predivna osoba

Maryam Mirzakhani, jedina žena dobitnica Fieldsove Medalje, umrla je u 41. godini života. Borila se s rakom dojke od 2013.

Fieldsovu medalju, najviše matematičko priznanje koje se dodjeljuje svake četiri godine, dobila je 2014. za svoje rezultate u geometriji i dinamici zakrivljenih površina s mogućim primjenama u kriptografiji i teorijskoj fizici (poglavito u istraživanju porijekla svemira i kvantnoj teoriji polja).

Sebe je nazivala “sporom matematičarkom”, no svima je bilo jasno da se tu nije radilo o sporosti nego o hvatanju ukoštac s izuzetno teškim problemima (kojima se drugi nisu htjeli ili još češće nisu mogli baviti) i dubokom “kopanju” do samih temelja.

Radila je na velikim listovima papira crtajući mnoštvo dijagrama okruženih složenim formulama, pa je njena malena kći na pitanje “što radi mama” jednostavno odgovarala da “mama crta”.

Rođena je u Teheranu i ranu joj je mladost obilježio Iransko-irački rat. Ravnatelj njene ženske gimnazije bio je dovoljno nepokolebljiv da je ubaci u iransku ekipu za Matematičku olimpijadu 1994. (u koju nikada prije nije uvrštena jedna djevojka) i tada je osvojila zlatnu medalju. Na sljedećoj Olimpijadi 1995. opet je osvojila zlato, sada sa 100% rezultatom.

Nakon diplome na Sveučilištu Šarif u Teheranu upisala je doktorski studij na Harvardu. Mentor joj je bio C. McMullen, još jedan osvajač Fieldsove medalje, koji je opisuje kao ženu “koja matematici prilazi neustrašivo”.

Njena disertacija iz 2004. malo je remek djelo. Riješila je dva dugo neriješena problema, koji bi svaki za sebe bio vrijedan disertacije, i još ih k tome povezala na nočekivani način. Većina matematičara nikada ne stvori nešto tako kvalitetno, a ona je to uspjela već u svojoj disertaciji. Uistinu spektakularno.

Poslije Harvarda dobila je poziciju na Princetonu i potom na Stanfordu 2008. Tu je zajedno s A. Eskinom, radila na problemu trajektorija “biljarskih kugli” na “stolovima” raznih oblika (kojim si mnogi fizičari i matematičari razbijaju glave već sto godina). Njihovo je istraživanje rezultiralo člankom od preko 200 strana, koji je objavljen 2013. i koji je proglašen “titanskim radom kojim počinje jedna nova era u matematici”.

Fieldsova medalja je zaista zaslužena.

Sam dolazak na Svjetski kongres matematičara u Seul 2014, na kojem joj je dodijeljena medalja, bio je veliki izazov za Mirzakhani. Iako to tada nije obznanila, bila je u jeku borbe s okrutnom bolešću.

Kao prva žena dobitnica Medalje (i prva iz Irana) bila je pod velikim pritiskom. Osim uobičajenog  publiciteta i očekivanja da bude uzor mnogim mladim matematičarima i posebno matematičarkama diljem svijeta, podizala je svoju kćerkicu i borila se s rakom. I uz to je ostala znanstveno izuzetno aktivna (nedavno je s A. Eskinom poopćila je jedan rezultat Marine Ratner koja je nesretnom koincidencijom umrla dan prije Mirzakhani u 78. godini). Nastavila je s radom do pred samu smrt.

Bila je jedan od najvećih umova našeg vremena i prema jednoglasnim svjedočenjima kolega i prijatelja predivna osoba.

Iza nje ostala je kći Anahita, muž, roditelji, sestra i dva brata. Sigurno će im nedostajati kao što će nedostajati i matematici 21. stoljeća kojoj je mogla još mnogo toga dati.

I na kraju par riječi za one koji žele bar mali uvid u matematiku kojom se bavila.

Radovi su joj vezani uz Riemannove plohe i u njima povezuju više matematičkih područja – hiperboličku geometriju, kompleksnu nalizu, topologiju i teoriju dinamičkih sustava.

Riemannove plohe možemo zamišljati kao proizvoljne plohe u prostoru (sfere, torusi i sl.), no ključni Riemannov uvid (još iz 19.st.) bio je da ih možemo definirati i izučavati neovisno od prostora u koji su smještene (te da neke i ne možemo smjestiti u 3-dimenzionalni prostor, iako ih je uvijek moguće smjestiti u neki višedimenzionalni prostor).

Početkom 20.st. matematičari su shvatili da ih je topološki moguće karakterizirati jednim jedinim brojem, genusom g te plohe, koji predstavlja broj njenih „drški“. Npr. sljedeće plohe imaju g = 3 i g = 2.

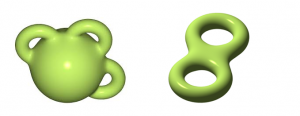
To znači da se dvije Riemannove plohe istoga genusa mogu topološki (tj. rastezanjem i stezanjem, ali bez kidanja) transformirati jedna u drugu, dok za one različitih genusa to nije moguće.

Npr. ploha šalice za kavu i ploha automobilske gume obje imaju g = 1, pa se mogu topološki transformirati jedna u drugu, a što se može vidjeti ovdje.

Nasuprot tome, nijedna od njih se ne može topološki transformirati u sferu čiji je g = 0.

Nadalje, svaka se Riemannova ploha može identificirati s kompleksnom algebarskom strukturom, kao što se obična ravnina može može identificirati sa strukturom kompleksnih brojeva.

Sjetite se srednjoškolske identifikacije kompleksnih brojeva s točkama ravnine:

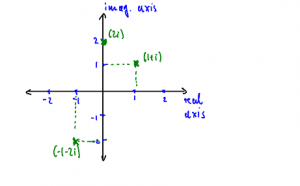
Ta identifikacija omogućava da se Riemannove plohe izučavaju metodama kompleksne analize, tj. metodama infinitezimalnoga računa u području kompleksnih brojeva.

U tom kontekstu svaka Riemannova ploha postaje algebarskom krivuljom, jer ploha koja je 2-dimenzionalni objekt u odnosu na 1-dimenzionalne realne brojeve (kao koordinate), postaje 1-dimenzionalni objekt u odnosu na 2-dimenzionalne kompleksne brojeve (kao koordinate).

Naravno, Riemannova ploha može se izučavati i uobičajenim geometrijskim metodama; uz pomoć mjerenja duljina, kuteva, površina i sličnih geometrijskih veličina na toj plohi. Takva jedna geometrija, vezana uz određeni tip ploha, je slavna hiperbolička geometrija Gaussa, Bolyaia i Lobačevskog.

Ovi različiti pristupi Riemannovim plohama (putem topologije, kompleksne analize i npr. hiperboličke geometrije) izvor su mnogih dubokih uvida u njihov svijet, uvida za koje je u velikoj mjeri zaslužna i Mirzakhani.

Za plohe je jedan od najvažnijih pojmova pojam geodetske linije. To su one linije koja na najkraći način povezuju svoje točke (npr. u ravnini to su pravci, a na sferi tzv. glavne kružnice sa središtem u središtu sfere).

Prije pola stoljeća dokazan je danas klasični teorem koji kaže da broj zatvorenih geodetskih linija kraćih od N raste eksponencijalno, tj. jednak je e^N / N za velike N.

Taj se teorem naziva „teoremom prostih brojeva za geodetske linije“ jer je potpuno analogan „teoremu prostih brojeva“ u aritmetici, koji kaže da je broj prostih brojeva manjih od e^N jednak e^N / N za velike N (što vjerojatno nije slučajno i cijelu tu teoriju povezuje s aritmetikom).

Rivin je dokazao da u slučaju zatvorenih geodetskih linija koje su jednostavne (tj. ne sijeku se same sa sobom) odgovarajući broj ne raste eksponencijalno nego polinomialno, tj. za velike je N jednak N6g-6, gdje je g genus plohe. Mirzakhani je tu ocjenu smjestila u bitno prirodniji kontekst.

Njen pristup ovim pitanjima i metode koje je razvila omogućili su joj da na nov i iznenađujuć naćin dokaže slavnu Wittenovu hipotezu koja teorijsku fiziku duboko veže uz matematiku (riječima Atiyaha, možda najvećeg živućeg matematičara „fizika opet daje duboke uvide u same temelje matematike i matematičari ponovo obraćaju pažnju na svoje povijesne korijene u fizici“).

To su, naravno, samo neki od njenih rezultata, a i oni tek ovlaš naznačeni.