Matematički model imuniteta stada. Dani, koeficijenti, širitelji zaraze, zaraženi, oporavljeni. Žrtve

Problem je točno procijeniti parametre β i γ koji se pojavljuju u ovom modelu epidemije, piše Zvonimir Šikić. Problem je dakle procijeniti broj kontakata kojima se širi zaraza, kao i broj onih koji je prevladaju ili joj podlegnu. Najjednostavnije rečeno, kako u populaciji raste omjer onih koji su prošli zarazu tako se smanjuje mogućnost njezinog širitelja da nekog zarazi

• Naslovna fotografija: Prazan Stradun, ulica u gradu koji je izmislio karantenu (The Dubrovnik Times)

S obzirom da se projekcije razvoja epidemije temelje na matematičkim modelima pokušat ću objasniti najjednostavniji matematički model širenja zaraze koji je temelj svih složenijih i preciznijih modela. (Ako se plašite formula samo preletite preko njih.)

Označimo sa S(t) broj ljudi koji su na dan t podložni infekciji, s I(t) broj infektivnih na taj dan i s R(t) broj onih koji su prebrodili infekciju i na taj dan više nisu infektivni (tu spadaju i umrli). Kratice dolaze od engleskih termina susceptible, infected i resistant, a mi ćemo ih zvati sumnjivima, inficiranima i rezistentnima. Model koji opisujem iz očitih se razloga zove SIR model.

Ako je N ukupni broj ljudi u populaciji koju promatramo onda sa s(t) označavamo dio populacije koji je sumnjiv na dan t. Drugim riječima s(t) =S(t)/N. Analogno, dio populacije koji je infektivan na dan t označavamo s i(t), a dio populacije koji je rezistentan na dan t označavamo s r(t). Drugim riječima i(t) =I(t)/N i r(t) =R(t)/N. Dakle, svaki dan t vrijedi:

S(t) + I(t) + R(t) = N

tj.

s(t) + i(t) + r(t) = 1 (1)

Pretpostavimo da svaki inficirani prosječno u jednom danu (dt = 1) ima β opasnih susreta u kojima može prenijeti infekciju. Tada će on od dana t do sljedećeg dana t +dt inficirati βs(t) sumnjivih. Dakle, on će βs(t) sumnjivih prevesti u inficirane. Ukupni broj sumnjivih smanjit će se za βs(t) I(t) jer je na dan t infektivnih ukupno I(t). Dakle ukupna promjena sumnjivih u tom danu je:

dS = -βs(t) I(t) dt

tj.

ds/dt = -βs(t) i(t) (2)

Pretpostavimo nadalje da se u jednom danu oporavi (ili umre) γ-ti dio inficiranih, koji time postaju rezistentni. Tada je ukupna promjena rezistentnih u tom danu:

dR = γI(t) dt

tj.

dr/dt = γi(t) (3)

Iz (1) slijedi

ds/dt + di/dt + dr/dt = 0 (4)

Iz (2), (3) i (4) slijedi

di/dt = -ds/dt – dr/dt = βs(t) i(t) – γi(t)

Na početku epidemije nekim novim infektom sumnjivi su svi, s(0) = 1, a rezistentnih još nema, r(0) = 0. Ako je početno samo jedan inficiran onda imamo i(0) = 1/N ≈ 0.

Sve u svemu, veličine s(t), i(t) i r(t) zadovoljavaju diferencijalne jednadžbe

ds/dt = -βs(t), i(t) dr/dt = γi(t), di/dt = βs(t) i(t) – γi(t)

i početne uvjete

s(0) = 1, i(0)≈1/N, r(0) = 0.

Ovakve diferencijalne jednadžbe obično se rješavaju numerički. Npr. za β = 1/2 i γ = 1/3 numerički dobivena rješenja s(t), i(t) i r(t) izgledaju ovako:

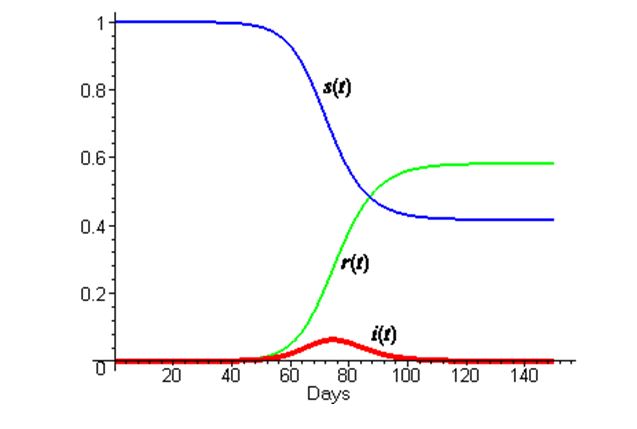
(Na sljedećoj stranici možete eksperimentirati s različitim β i γ)

Pogledajte što se na kraju desilo u ovom slučaju koji inače modelira hongkošku gripu iz sezone 1968/9. Nakon 150 dana više nije bilo inficiranih, i(t) = 0. Rezistentnih je bilo nešto manje od 60%, r(t) = 0.6. Sumnjivih, dakle nerezistentnih, ostalo je nešto više od 40%, s(t) = 0.4.

Kod sljedeće infekcije istim virusom epidemija će početi s vrijednostima r(0) = 0.6, s(0) = 0.4 i i(0) ≈0, tj. počet će na stabilnom kraju gornjega grafa. No, to znači da će u tom stabilnom stanju i ostati (jer se graf dalje ne mijenja). Dakle, populacija je postala stabilna sa 60% rezistentnih i više nije podložna epidemiji nego samo pojedinim slučajevima (kaže se da je postignut „imunitet stada“).

Na kakvo postupanje upućuje model koji za dane β i γ ima rješenje opisanoga oblika?

Ako je smrtnost inficiranih zanemariva, moguća taktika obrane jest da pustite patogen da inficira 60% populacije koja će tako steći imunitet stada.

Ako smrtnost nije zanemariva možda znate koji dio populacije s patogenom nema problema pa, ako je taj dio veći od 60%, možete patogen pustiti da inficira taj dio populacije. Tako će cijela populacija steći imunitet stada, bez žrtava. Naravno, u tom slučaju morate dobro izolirati onaj dio populacije koji s patogenom ima problema, što baš i nije jednostavno. Možda je to švedska taktika u slučaju trenutne korona epidemije: izoliraj stare i bolesne, a mlade puštaj da se inficiraju i stvore imunitet stada za cijelu populaciju.

Ako to nije slučaj onda (do postizanja imuniteta stada) širenje zaraze morate toliko usporiti da vam zdravstveni sustav može prihvatiti i uspješno liječiti sve one koji se ozbiljno razbole. U slučaju trenutne korona epidemije to je u stanju malo koji sustav i stoga ga je potrebno prilagoditi tom pritisku. Kako se to radi pokazuju postupci kojima Hrvatska usporava epidemiju i prilagođava svoj zdravstveni sustav.

Najbolje je, naravno, da imate cjepivo i procijepite 60% populacije. Tako dobijete 60% rezistentnih i imate imunitet stada bez žrtava. Za trenutnu epidemiju, nažalost, cjepiva neće biti još najmanje godinu dana.

No, vratimo se samom modelu. U njemu je problem točno procijeniti parametre β i γ. Parametar γ, tj. dio inficiranih koji u jednom danu izlazi iz infekcije moguće je procijeniti praćenjem oporavaka i smrti. On je, u grubo, recipročna vrijednost trajanje infektivnog perioda, ako je taj period približno isti za sve inficirane.
Parametar β (broj dnevnih susreta u kojima inficirani može prenijeti infekciju) može se procijeniti na posredni način. Promotrimo omjer:

β/γ = βx(1/γ) = (broj opasnih dnevnih susreta po inficiranom) x (broj dana infekcije)
= broj opasnih susreta po inficiranom

Taj omjer c = β / γ zovemo kontaktnim brojem. On mjeri intenzitet zaraznosti patogena i može se procijeniti prateći tok epidemije. Ako znamo γ i c možemo izračunati β.

Naravno, ovaj simplificirani model ima mnoge pretpostavke koje nisu realne; homogenost populacije, dostupnost svakoga svakome itd. Njih uvažavaju sofisticiraniji modeli koji su stoga bliži stvarnosti. No, vjerujem da vam već i ovaj jednostavni model daje bolju sliku (od one koju ste do sada imali) o tome što se zbiva u epidemijama.