Matematika kolektivnog imuniteta. Faktori usporavanja zaraze, cijepljenje, heterogenost

Prag kolektivnog imuniteta na nekim će lokacijama biti veći, na drugima manji. I biološke razlike utječu. U početku virus zarazi ljude koji su osjetljiviji, a poslije epidemija raste sporije nego što se moglo očekivati ​​na temelju početne stope rasta. Ipak, jedini način da se zaustavi je postizanje kolektivnog imuniteta svuda, a ne samo ondje gdje su zaraze bile najviše

• Naslovna ilustracija: Oxford Vaccine Group

Ako neku glasinu prenesete samo jednoj osobi te ako je ta osoba sljedeći dan prenese jednoj novoj osobi, itd. trač se neće proširiti daleko. Nakon 30 dana proširit će se na 30 osoba.

Ako svaka osoba glasinu prenese na dvije nove osobe, tada će nakon 30 dana glasina doprijeti do više od milijardu ljudi; 2³⁰ = 1.073.741.824. Kako takva naizgled mala promjena – prenošenje na dvije osobe umjesto na samo jednu – može napraviti tako veliku razliku?

Radi se o bitnoj razlici između linearnog i eksponencijalnoga rasta. Linearni rast je spor i stabilan, sa stalno istim dnevnim prirastima. U našem slučaju 1 osoba dnevno. S druge strane, eksponencijalni rast karakteriziraju prirasti koji se multipliciraju: 2 nove osobe prvi dan, 4 nove osobe drugi dan, 8 osoba treći dan, 16 osoba četvrti dan itd. Za razliku od linearnog rasta, eksponencijalni rast se ubrzava – brzina rasta i sama raste. To dovodi do razlike između 30 osoba (na grafu žuto) i milijarde osoba (na grafu plavo) koje su čule glasinu nakon 30 dana.

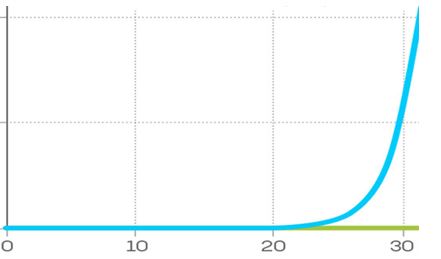
Infekcije se šire poput glasina. Netko ih pokupi i proslijedi nekom drugom. Naravno, postoje razlike, ali isti matematički model koristan je u obje situacije. U našem jednostavnom primjeru vidjeli smo kako naizgled mala razlika u brzini prijenosa glasine stvara veliku razliku u tome koliko ju je ljudi u konačnici čulo. Isto vrijedi za zarazne bolesti. Razlika između prenošenja infekcije na jednu osobu i prenošenja na dvije osobe razlika je između nekoliko izoliranih slučajeva i epidemije.

Infekcije se šire brzinom koja ovisi o mnogim biološkim i socijalnim faktorima. Epidemiolozi pokušavaju sažeti utjecaj svih tih faktora u “osnovni reprodukcijski broj” infekcije, koji označavaju s R₀. To je prosječni broj novih infekcija koji u zaraznom razdoblju prouzroči svaka zaražena osoba. U kontekstu našeg primjera prenošenja glasina, osnovni reprodukcijski brojevi bili su R₀ = 1 (svaka osoba prenosi glasinu na 1 novu osobu) i R₀ = 2 (svaka osoba prenosi glasinu na 2 nove osobe), a „zarazno razdoblje“ bilo je jedan dan.

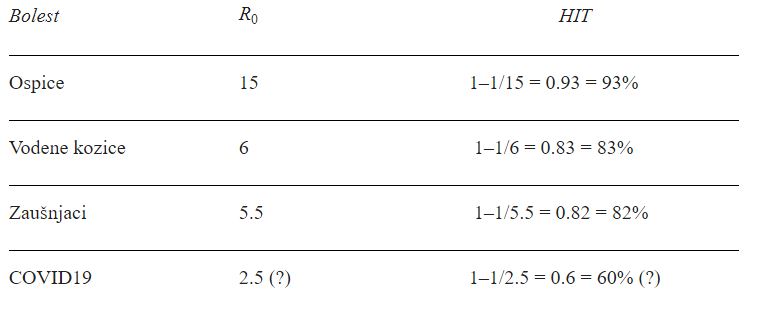
Evo osnovnih reprodukcijskih brojeva nekih poznatih infekcija.

Uočite da su svi reprodukcijski brojevi veći od 1. To je jedan od razloga zašto su te bolesti opasne. Budući da će svaka zaražena osoba zaraziti više od jedne osobe, broj zaraženih će eksponencijalno rasti, što može biti pogubno. Zato je ključno pitanje možemo li R₀ svesti na 1.

Razmislimo o tome što nam govori osnovni reprodukcijski broj. Na primjer, R₀ = 2 znači da će zaražena osoba (u prosjeku) zaraziti 2 nove osobe. Ako se zaražena osoba u razdoblju zaraze susretne s 10 ljudi, svi kontaktirani imaju šanse biti zaraženi, ali činjenica da je R₀ = 2 znači da će se (u prosjeku) zaraziti 2 od ovih 10 osoba. Dakle, svaka od tih 10 osoba ima 2/10, ili 20 %, šanse da se zarazi.

Pretpostavimo sada da su dvije od tih 10 osoba cijepljene pa se ne mogu zaraziti. No, svaka od preostalih 8 osoba još uvijek ima 20 % šanse da se zarazi. To znači da će u prosjeku biti zaraženo 20 % od tih 8 osoba, što je 1,6.

Dakle, ako su dvije od deset osoba cijepljene, tada će jedna zaražena osoba (u prosjeku) zaraziti samo 1,6 osoba. Cijepljenjem je osnovni reprodukcijski broj ove bolesti smanjen s R₀ = 2 na R₀ = 1,6.

Možemo li  osnovni reprodukcijski broj svesti na 1 kako bismo izbjegli eksponencijalni rast?

Opet pretpostavimo da naša zaražena osoba dolazi u kontakt s 10 osoba tijekom zaraznog razdoblja i da svaka necijepljena osoba ima 20 % šanse da se zarazi. Pretpostavimo da je C od tih 10 osoba cijepljeno. Tada će se zaraziti 20 % od 10 – C necijepljenih osoba ili 0,2 × (10 – C). Da bi rast bio linearan, a ne eksponencijalan, prosječan broj novih infekcija mora biti 1. Dakle, moramo riješiti jednadžbu:

0,2 × (10 – C) = 1.

Rješenje je C = 5. Dakle, cijepljenjem 5 od 10 osoba, tj. 50% osoba, R₀ smo reducirali na 1.

Taj se postupak može generalizirati za bilo koji R₀. Ako pretpostavimo da svaka zaražena osoba kontaktira N novih osoba u zaraznom razdoblju, tada možemo očekivati da će u prosjeku R₀/N tih osoba biti zaraženo. Ali ako je C broj cijepljenih među N kontaktiranih, onda (R₀/N) (N – C) predstavlja broj novo zaraženih. Želimo da on bude 1 pa imamo jednadžbu

(R₀/N) (N – C) = 1

iz koje odmah slijedi

C/N = 1 – 1/R₀.

Dakle, ako procijepimo 1 – 1/R₀ populacije svaka će zaražena osoba zaraziti samo 1 novu osobu, tj. 1 – 1/R₀ čarobni je postotak koji rezultira linearnim, a ne eksponencijalnim rastom bolesti.

Na toj razini procijepljenosti populacija postiže kolektivni imunitet. To nije imunitet pojedinaca, nego redukcija eksponencijalnoga rasta zaraze na linearni. Postotak cijepljenja potreban za postizanje kolektivnog imuniteta naziva se „prag kolektivnog imuniteta” (s kraticom HIT za “herd immunity threshold”). Evo HIT-ova za gornje zarazne bolesti.

Očito je da cijepljenje ne pruža potencijalnu korist samo cijepljenom pojedincu, nego i necijepljenim pojedincima u populaciji. Budući da je manje vjerojatno da će se bolest široko proširiti, svi su u manjem riziku, uključujući i one koji nisu cijepljeni. To je posebno važno za osobe kojima cijepljenje nije medicinski preporučljivo, poput novorođenčadi ili starijih i nemoćnih osoba.

Da zaključimo, dramatičnu razliku između linearnog i eksponencijalnog rasta, koja je za mnoge razlika između života i smrti, moguće je premostiti odgovarajućim procjepljivanjem populacije i to je jedna od najvećih blagodati medicine uopće.

Do sada opisano samo je prva aproksimacija. Jednostavna formula za izračunavanje praga kolektivnog imuniteta, za R₀ = 2,5 u slučaju COVID-19, daje prag 1 – 1/2.5 = 0,6 ili 60%. Virus će se širiti eksponencijalno sve dok 60% populacije ne postane imuno, a od tog će se trenutka širiti linearno dok se potpuno ne zaustavi.

No, R₀ zapravo nije konstanta nego varira od slučaja do slučaja. Zaražena osoba na svadbi može zaraziti mnogo više ljudi od zaražene osobe u samoizolaciji. To znači da će prag kolektivnog imuniteta na nekim lokacijama biti veći od 60%, a na nekim drugim manji. Osim toga, razlike u ponašanju dovode do toga da su neki ljudi izloženiji bolesti od drugih. Naravno, i biološke razlike utječu na vjerojatnost zaraze. Rađamo se različiti i te se razlike akumuliraju kroz naša različita životna iskustva, što sve utječe na našu sposobnost da se borimo protiv virusa. Sve to ima važne implikacije za izračun praga kolektivnog imuniteta.

Epidemiolozi te varijacije nazivaju heterogenošću osjetljivosti na infekciju i ona utječe na prag kolektivnog imuniteta. Ona će taj prag u nekim slučajevima povećati; na primjer u staračkim domovima, gdje je prosječna osoba osjetljivija na COVID-19 od prosječne osobe u široj populaciji. Ali u cijeloj populaciji, heterogenost obično snižava prag kolektivnog imuniteta. U početku virus zarazi ljude koji su osjetljiviji i brzo se širi. Da bi se nastavio širiti, virus se mora prebaciti na ljude koji su manje osjetljivi. To otežava širenje virusa, pa epidemija raste sporije nego što se moglo očekivati ​​na temelju njegove početne stope rasta.

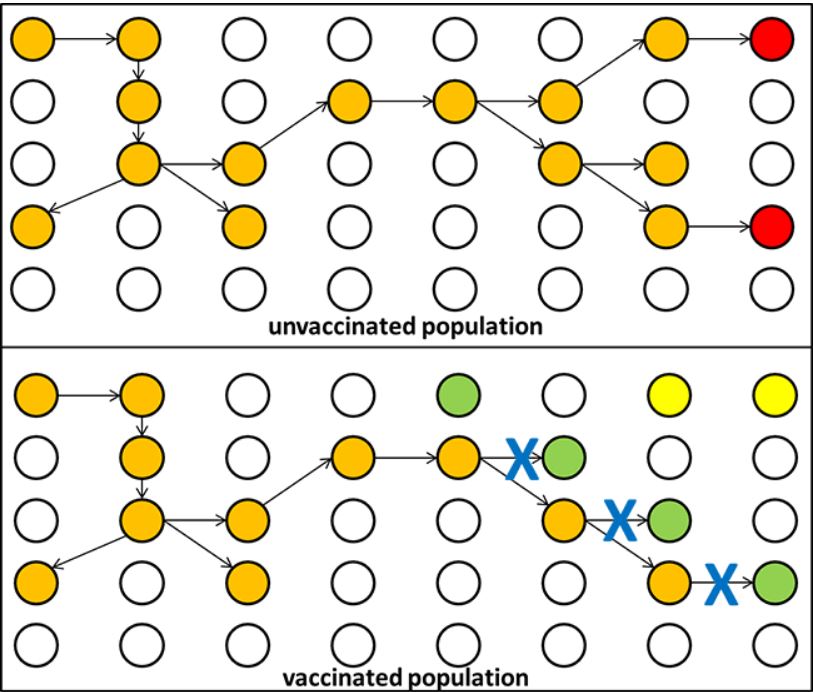
Ilustracija: Oxford Vaccine Group

Ključno je pitanje koliko je niži prag kolektivnog imuniteta u uvjetima heterogenosti. Prema jednostavnom modelu, 60% populacije trebalo bi preboljeti COVID-19 ili biti  cijepljeno, kako bi se zaustavilo širenje bolesti. Ali mnogi stručnjaci smatraju da bi zbog heterogenosti prag kolektivnog imuniteta mogao biti između 40% i 50%. To su uglavnom kvalitativne procjene, jer je teško kvantificirati što jednu osobu čini osjetljivijom od druge.

No, ima i pokušaja kvantifikacije. Science je u lipnju objavio članak koji kvantificira stupanj heterogenosti i procjenjuje prag kolektivnog imuniteta za COVID-19 na 43%. Jedan od koautora članka (Tom Britton sa Sveučilišta u Stockholmu) smatra da postoje dodatni izvori heterogenosti koji njihov model nije uzeo u obzir i koji bi prag mogli dodatno smanjiti. Studija objavljena na MedRxiv (koja još nije prošla znanstvenu recenziju) procjenjuju da bi prag kolektivnog imuniteta stada na COVID-19 mogao biti niži od 20%. Ako je to točno, najteže pogođena mjesta na svijetu već su blizu toga praga.

Međutim, mnogi stručnjaci smatraju da studije koje prag spuštaju na 20% nisu pouzdane. J. Shaman sa Sveučilišta Columbia smatra da kolektivni imunitet od 20% nije u skladu s drugim respiratornim virusima, npr. s gripom (zašto bi bio toliko manji za jedan respiratorni virus u odnosu na drugi).

Kako bilo, jedini način da se zaustavi pandemija COVID-19 jest postizanje kolektivnog imuniteta svugdje, a ne samo na malom broju mjesta gdje su zaraze bile najviše. To će se vjerojatno dogoditi tek kada (i ako) cjepivo bude masovno primijenjeno.

U međuvremenu, kako bi se spriječilo širenje virusa i smanjio njegov R₀, preostaje distanciranje, maske i traženje kontakata, bez obzira na to gdje se između 20% i 60% smjestio prag kolektivnog imuniteta.