Matematika neuronskih mreža. Je li ChatGPT simplificiran model ljudskog mozga?

U članku o umjetnoj inteligenciji Zvonimir Šikić objašnjava kako se generativni pretrenirani transformatori koriste za stvaranje pisanih sadržaja. Opisuje princip rada i treniranja neuronskih mreža, ali i ograničenja, te zaključuje kako svejedno mogu pokazati da su neke ideje, na prvi pogled nezamislive, ipak zamislive, možda i realne.

• Naslovna fotografija: Stilizirani prikaz digitalne neuralne mreže (Midjourney v6)

ChatGPT je AI chatbot koji na zahtjev generira pisane sadržaje, uključujući članke, objave na društvenim mrežama, eseje, kodove i sl. GPT je kratica za Generative Pre-trained Transformer, što opisuje način na koji ChatGPT obrađuje zahtjeve i formulira odgovore. Korisnici mu mogu postavljati bilo kakva pitanja, uključujući složena poput “Što je smisao života?” ili jednostavna poput “Koje je godine Biden postao predsjednik SAD?” (ChatGPT koristi podatke do 2021. godine, tako da nema saznanja o događajima i podacima nakon te godine).

Svestran je i može se koristiti za više od pukog razgovora. Ljudi su ga npr. koristili za:

• kodiranje računalnih programe i nalaženje grešaka u kodu,
• skladanje glazbe,
• sažimanje članaka, podcasta ili prezentacija,
• rješavanje matematičkih zadataka,
• igranje igara,
• jednostavnije opisivanje složenih tema, i tako dalje.

Neke koristi upotrebe ChatGPT-a uključuju sljedeće:

• Učinkovit je, jer se lako nosi s rutinskim zadacima, što omogućuje ljudima da se usredotoče na složenije probleme.
• Štedi troškove, jer je isplativiji od zapošljavanja i obuke dodatnih zaposlenika.
• Obrazuje i osposobljava, jer se može koristiti kao virtualni učitelj.
• Brz je. Pruža gotovo trenutne odgovore.
• Dostupan je 0-24.
• Može komunicirati na mnogo jezika.
• Personaliziran je, jer se prilagođava korisničkim preferencijama i ponašanjima na temelju prethodnih interakcija.

Neka ograničenja upotrebe ChatGPT-a uključuju sljedeće:

• Ne „razumije“ u potpunosti složenost ljudskog jezika pa se njegovi odgovori katkada čine plitkima i bez pravog uvida.
• Budući da se temelji na predviđanju sljedeće riječi (v. dolje), pretjerano se koristiti nekim riječima pa ljudi ipak moraju uređivati sadržaj koji im nudi.
• Dobro sažima, ali ne navodi izvore niti pruža analizu podataka koje daje (kada i daje neku statistiku ne objašnjava što ta statistika znači).
• Može se usredotočiti na pogrešan dio pitanja i iz toga se ne može izvući. Na primjer, ako ga pitate “Je li konj dobar ljubimac s obzirom na njegovu veličinu?” a zatim ga pitate: “A što je s mačkom?” usredotočit će se isključivo na njenu veličinu kao kriterij.

Iako ChatGPT može biti od velike pomoći, postoje i mnogi etički problemi koji su vezani uz njegovo korištenje, uključujući pristranost, nedostatak privatnosti i sigurnosti te varanje u obrazovanju i na poslu. No to sve nisu naše teme. Naša je tema sljedeća.

• Kako radi ChatGPT

Počnimo s jednim primjerom. Kada sam zatražio ChatGPT da mi odgovori na pitanje „What politics can be?“ dobio sam sljedeći tekst.

Politics can be a multifaceted and significant part of society, shaping many aspects of our lives and influencing the direction in which our communities and countries are headed. From laws and policies to budgets and regulations, politics touches every aspect of governance and public life.

At its core, politics is about the exercise of power and the distribution of resources within a society. It involves complex negotiations, power struggles, and decision-making processes that can have far-reaching consequences for individuals and groups. Whether it’s debates over healthcare, education, the environment, or national security, political decisions can have a profound impact on people’s lives.

In addition to shaping public policy, politics also plays a role in shaping culture and society. Political leaders and movements can influence public opinion, shape social norms, and inspire collective action. Through media, public discourse, and public events, politics can play a central role in shaping the values and beliefs of a society.

Ultimately, politics is about the allocation of power and resources, and the ways in which individuals and groups come together to make decisions that affect us all. It is through politics that we navigate the complexities of our diverse societies, seek to address challenges, and work towards a better future for all.

Kako je ChatGPT generirao taj tekst? Najjednostavnije kazano, krenuo je od zadanog „Politics can be“ i zatim je generirao razumni nastavak riječ po riječ. Tu se pod “razumnim nastavkom” misli na generiranje sljedeće riječi kao one koju očekujemo da će netko napisati kao sljedeću nakon što svoj dosadašnji tekst usporedi s tekstovima na milijardama web stranica. Na primjer, kada je ChatGPT već generirao tekst „Politics can be a multifaceted and significant“ sljedeća je riječ mogla biti (što sam provjerio pitajući ga):

1. …influence
2. …determinant
3. …platform
4. …part
5. …tool
6. …reflection
7. …opportunity

Iako to zvuči gotovo nevjerojatno ChatGPT producira suvisle tekstove na ovaj gotovo banalni način. Dakle, on se uvijek iznova pita “s obzirom na do sada napisani tekst koja bi trebala biti sljedeća riječ?” i kada nađe odgovor naprosto doda tu riječ. Točnije, on dodaje tokene, koji mogu biti i samo dio riječi, zbog čega ponekad može “izmisliti“ nove riječi, no to ćemo ovdje zanemariti.

Još točnije, ChatGPT u svakom koraku ukupnom popisu riječi pridružuje vjerojatnosti njihovog pojavljivanja u stvarnim tekstovima. Mogli biste pomisliti da nakon toga odabire onu riječ kojoj je pridružena najveća vjerojatnost, no on to ne radi. Ako bi uvijek izabirao najvjerojatniju riječ producirao bi vrlo “flah” tekstove koji ne pokazuju nimalo kreativnosti. Ali ako ponekad (nasumce) bira lošije rangirane riječi, ChatGPT producira “zanimljivije” tekstove. (Naravno, taj slučajni odabir znači da ćemo na ponovljeni upit vjerojatno dobiti različit odgovor.) Pokazalo se da odlične rezultate dobiva ako lošije rangirane riječi bira u 80% slučajeva.  Za sada nitko ne zna zašto je to tako. To je tek eksperimentalna činjenica koju ćemo, nadamo se, jednoga dana moći i objasniti.

Kako ChatGPT računa vjerojatnosti kandidata za sljedeću riječ? Na raspolaganju mu je cca 40 000 engleskih riječi. Ako ima dovoljno veliki korpus engleskih tekstova onda bi kao vjerojatnost  neke riječi , mogao uzeti frekvencija pojavljivanja riječi  u tom korpusu. Korpus dostupan na internetu sadrži cca 400 milijardi riječi (tj. svaka se riječ u njemu pojavljuje prosječno 10 milijuna puta) što frekvenciju čini dobrom aproksimacijom vjerojatnosti.

Kolika je vjerojatnost \({\small P(x|y)}\) neke riječi y pod uvjetom da joj prethodi riječ x? Po definiciji (i zdravo razumskom razumijevanju) uvjetne vjerojatnosti ona je:

\(
P(y|x) = \frac{\displaystyle P(xy)}{\displaystyle P(x)}
\)

Dakle, osim frekvencije riječi x potrebno je znati frekvencija para riječi xy. Takvih parova ima 40.000 · 40.000 = 1,6 milijardi (tj. svaki se takav par riječi u korpusu pojavljuje prosječno 250 puta) što frekvenciju još uvijek čini dobrom aproksimacijom vjerojatnosti.

Kolika je vjerojatnost \({\small P(z|xy)}\) neke riječi z pod uvjetom da joj prethodi par riječi xy?

\(
P(z|xy) = \frac{\displaystyle P(xyz)}{\displaystyle P(xy)}
\)

Sada je osim frekvencije para riječi xy potrebno znati i frekvenciju slijeda od tri riječi xyz. Takvih trojki ima 40.000 · 40.000 · 40.000 = 64.000 milijardi, tj. ukupni broj takvih trojki je 160 puta veći od ukupnog korpusa u kojem bi ChatGPT trebao naći njihove frekvencije. To je, naravno, nemoguće.

Dakle, nemoguće je putem frekvencija procijeniti vjerojatnost sljedeće riječi već nakon slijeda od tri riječi, a da ne govorimo o procjeni nakon slijeda od npr. 100 riječi (što je za ChatGPT kratak tekst). Kako onda ChatGPT računa potrebne vjerojatnosti? Pomoću neuronskih mreža.

• Što su i što rade neuronske mreže

Neuronske mreže i njihov rad predstavit ćemo na zadatku koji one veoma uspješno rješavaju. To je prepoznavanje slika. Kao jednostavan primjer, razmotrimo slike slova:

­­

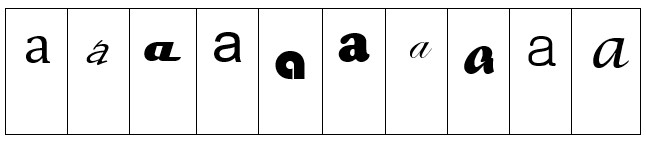
Problem je da se slova pojavljuju u mnogim oblicima, npr. u raznim fontovima (kao slovo a; v. dolje) ili pak u manje ili više čitljivim rukopisima. Kako te različite oblike prepoznajemo kao isto slovo?

­­

U ljudskom mozgu postoji oko 100 milijardi neurona (živčanih stanica). Svaki neuron šalje električne signale frekvencijom do tisuću impulsa u sekundi. Neuroni su povezani u kompliciranu mrežu u kojoj se svaki grana prema tisućama drugih, prenoseći im električne signale. Da li će neki neuron u danom trenutku poslati električni impuls i gdje će ga poslati, ovisi o tome koje je impulse primio od drugih neurona – s time da različite veze daju doprinose s različitim “težinama”.

Ono što se događa kada “vidimo sliku” je da fotoni svjetlosti koji se odbijaju od slike padaju na “foto receptorske” neurone u stražnjem dijelu našega oka gdje proizvode električne signale. Ovi neuroni šalju signale drugim neuronima, a ovi opet daljnjima  pa signali prolaze kroz cijeli niz slojeva neurona. U tom procesu mi “prepoznajemo” sliku i konačno “formiramo misao” da “vidimo slovo a”.

Matematizirana i simplificirana verzija biološke neuronske mreže je umjetna neuronska mreža. Jedna takva, s 11 slojeva neurona, konstruirana je 1998. i pokazala se uspješnom u prepoznavanju zadanih slika. Ona nije bila proizvod neke naročito razvijene teorije. Bila je rezultat inženjerskog postupka s mnoštvom pokušaja i pogrešaka. Ipak, osnovni princip rada (umjetnih) neuronskih mreža nije teško objasniti.

Podijelimo sliku na manja polja, tzv. pixele, npr. na 200 · 200 = 40.000 pixela. U slučaju crno-bijele slike svaki pixel ima neku nijansu sive boje. Te nijanse numeriramo, npr. od potpuno bijele 1 do potpuno crne 100. Onda je svaka slika jednoznačno reprezentirana nizom od 40.000 cijelih brojeva iz intervala 1 do 100. Takvih nizova ima 100⁴⁰⁰⁰⁰. Zadatak neuronske mreže je da svakom takvom nizu brojeva (koji predstavlja sliku) pridruži jedan cijeli broj između 1 i 30 (koji predstavlja naslikano slovo; a = 1, b = 2, c = 3, itd.).

Dakle, neuronska mreža treba računati funkciju y = f (x₁, x₂, … , x₄₀₀₀₀) na taj način da vrijednost y predstavlja baš ono slovo koje bi ljudi prepoznali baš na onoj slici koja je predstavljena nizom x₁, x₂, … , x₄₀₀₀₀. Naravno, ljudi nisu uvijek sigurni u svojim prepoznavanjima.

Razmotrimo mnogo jednostavniji 2-dimenzijski slučaj u kojem neuronska mreža treba računati funkciju 2 varijable y = f (x₁, x₂). U tom slučaju imamo samo 2 pixela x₁ i x₂ (kojima su moguće vrijednosti i dalje intenziteti sivila od 1 do 100), a moguće vrijednosti  neka su brojevi od 1 do 10. Sve moguće inpute (x₁, x₂) predstavljamo svim točkama kvadrata sa stranicom duljine 100 i pretpostavljamo da u deset istaknutih točaka (x₁, x₂) funkcija nedvojbeno prima vrijednosti 1, 2, … , 10, jer te slučajeve ljudi nedvojbeno prepoznaju.

­­

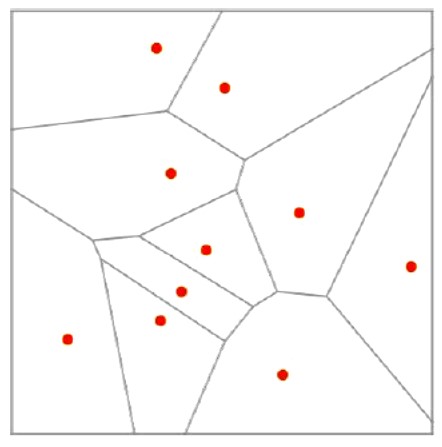
(U primjeru prepoznavanja slova, to odgovara onim točkama (x₁, x₂, … , x₄₀₀₀₀) u kojima funkcija nedvojbeno prima vrijednosti 1, 2, … , 30, tj. to odgovara onim slikama koje ljudi nedvojbeno prepoznaju kao slova a, b, … , ž.)

Svakoj „nedvojbenoj“ točki pridruženo je područje točaka koje su baš njoj najbliže.

(U primjeru prepoznavanja slova, to odgovara onim točkama koje će ljudi s nešto manje sigurnosti prepoznati kao slike odgovarajućih slova. Što je točka bliže „nedvojbenoj“ točki to je sigurnost veća, tj. sigurnost je to veća što se slika manje razlikuje od „nedvojbene“ slike.)

Da bismo objasnili kako neuronska mreža obavlja „zadatak prepoznavanja“ razmotrimo još jednostavniji primjer u kojem x₁ i x₂ primaju vrijednosti iz intervala [-1, 1], a y prima samo tri vrijednosti -1, 0, i 1 koje se „nedvojbeno“ postižu u istaknutim točkama kvadrata [-1, 1]  [-1, 1]. (U primjeru prepoznavanja slova, to bi bila tri slova a, b i c koja se „nedvojbeno“ prepoznaju kao a, b i c na odgovarajućim slikama.)

­­

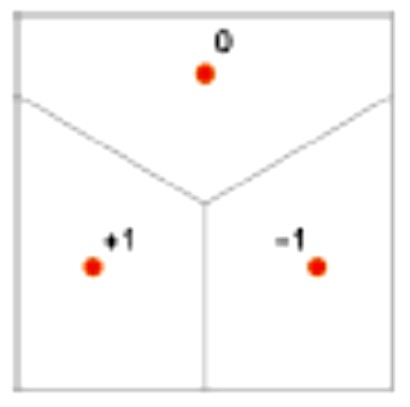
Neuronska mreža treba računati funkciju y = f (x₁, x₂) koja inputu (x₁, x₂) iz „područja 0“ pridaje vrijednost 0, onom iz „područja 1“ vrijednost 1 i onom iz „područja -1“ vrijednost -1. Kako ona to čini?

Neuronska mreža je povezan skup idealiziranih neurona složenih u slojeve. Na primjer:

­­

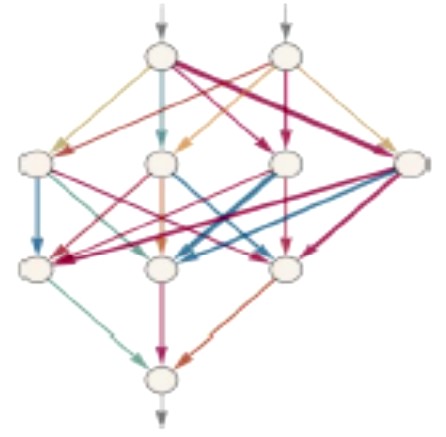
Svaki neuron računa jednostavnu numeričku funkciju tako da se ulazne vrijednosti (koje dolaze od neurona čije strelice upiru u taj neuron) množe s težinskim faktorima (koji su pridruženi tim strelicama) i zatim se zbroju tih umnožaka dodaje konstanta (koja je karakteristična za taj neuron). Na tu vrijednost konačno djeluje neka nelinearna funkcija poput ovih:

­­

Dakle, ako neuron ima inpute x = (x₁, … , x_k)  s težinskim faktorima w = (w₁, … , w_k) i ako mu je karakteristična konstanta b i ako se mreža pritom koristi nelinearnom funkcijom Tanh, taj će neuron izračunati vrijednost

\( Tanh(w \cdot x + b) = Tanh(w_1 x_1 + \ldots + w_k x_k + b) \)

i nju će s raznim težinskim faktorima proslijediti sljedećim neuronima. Tako se, polazeći od inputa (x₁, x₂) na vrhu, vrijednosti računaju i prenose do outputa na dnu. Na primjer, ovako bi moglo izgledati računanje vrijednosti  f (0.5, -0.8) = -1  (gdje tamnija i intenzivnija boja strelice opet odgovara njenoj većoj težini):

­­

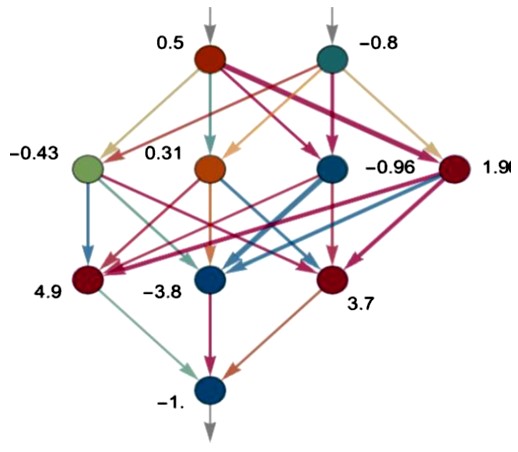
Matematički je dokaziva činjenica (tzv. teorem o univerzalnoj aproksimaciji) da se svaka funkcija (iz veoma široke klase funkcija) s bilo kojim brojem varijabli može aproksimirati na ovaj način. Na primjer, ako ranije razmatranu funkciju y = f (x₁, x₂) (koja ulaznim vrijednostima (x₁, x₂) iz „područja 0“ pridaje vrijednost 0, onima iz „područja 1“ vrijednost 1 i onima iz „područja -1“ vrijednost -1) grafički predstavimo tako da su 0, 1 i -1 predstavljeni žutom, bordo i plavom bojom

­­

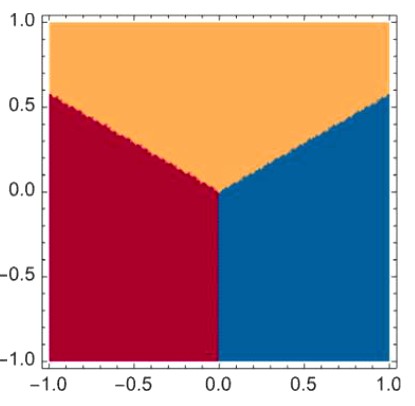
onda sa sljedećim neuronskim mrežama (uz optimalni odabir težinskih faktora) možemo postići sljedeće aproksimacije (opet, što je tamnija i intenzivnija boja strelice to je veća njena težina)

­­

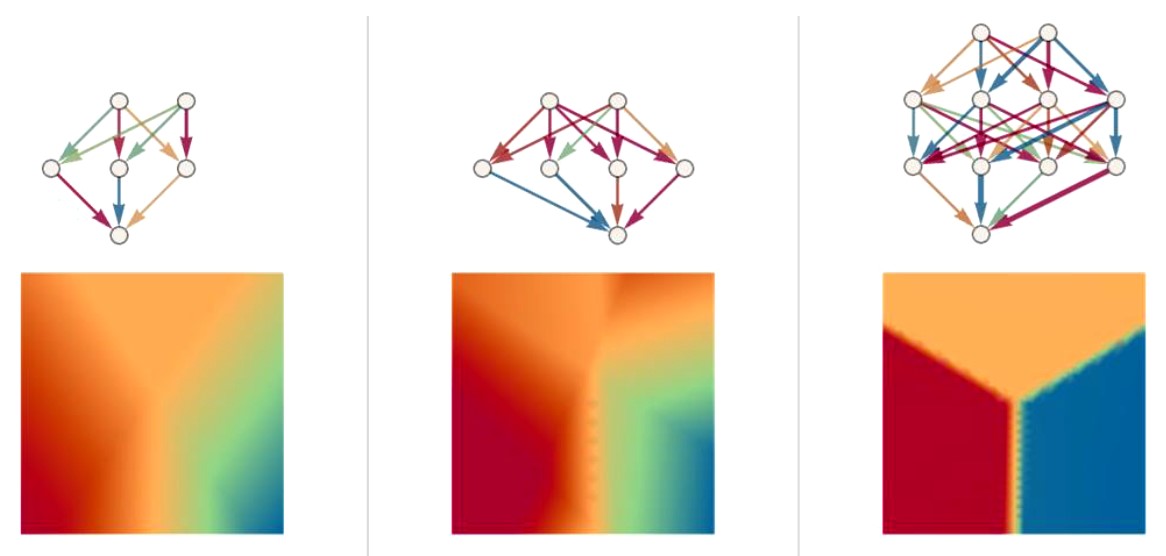
Rezimirajmo. Svaka slika se može predstaviti konačnim nizom brojeva x₁, … , x_n (koji su intenziteti sivila pojedinih pixela u slučaju crno-bijele slike), a svaki se opis slike može predstaviti jednim brojem y (koji određuje što vidimo na slici; 1= slovo a, 2 = slovo b, itd.). Na taj način problem rješavanja zadatka „Što je na slici?“ postaje problem računanja funkcije y = f (x₁, … , x_n).  Teorem o univerzalnoj aproksimaciji garantira da postoji neuronska mreža koja, uz optimalni odabir težinskih faktora, računa dobru aproksimaciju te funkcije i tako rješava postavljeni zadatak. Odabir što povoljnije mreže je inženjersko umijeće, no iskustvo nas uči da će svaka dovoljno velika mreža, uz dobar odabir težinskih faktora, biti uspješna. Pitanje je kako odrediti težinske faktore. Odgovor je: treniranjem neuronske mreže.

• Kako se treniraju neuronske mreže

Neuronske mreže (a vjerojatno i naši mozgovi) posebno su uspješne jer ih za obavljanje zadataka možemo trenirati na primjerima. Neuronska mreža koja razlikuje slova abecede nije  programirana da uočava ravne, zaobljene, vodoravne, okomite ili kose linije ni načine na koji su one povezane. Umjesto toga pokazujemo joj mnogo primjera raznih slova, ispravljamo njene krive odgovore (podešavanjem njenih težina) i to je način na koji ona “strojno uči” razlikovati slova. Tako utrenirana mreža “generalizira” iz prikazanih joj primjera na one koje nikad prije nije vidjela.

Kako se provodi taj trening i zašto je uspješan? Neuronsku mrežu čine uspješnom težine koje daju optimalnu aproksimaciju ciljane funkcije. Razmotrimo primjer funkcije jedne varijable y = f (x) koji je još jednostavniji od onih iz prethodnog odjeljka, a čiji graf izgleda ovako:

­­

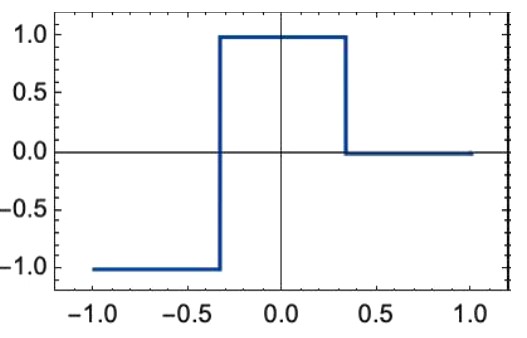
Nju treba generirati neuronska mreža s jednim inputom i jednim outputom, poput ove:

­­

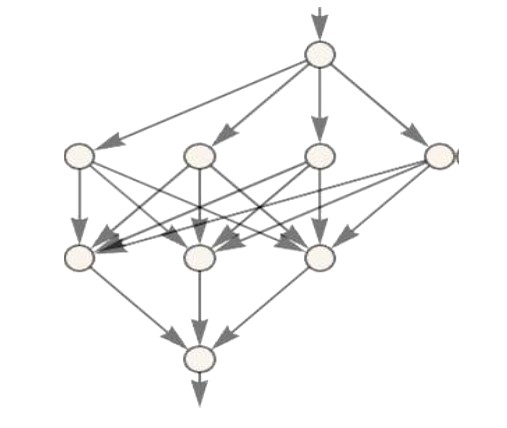
­Slučajno odabrane težine generirale bi funkciju koja evidentno nije dobra aproksimacija zadane funkcije; npr. funkciju čiji je graf dolje lijevo (odabrane težine w₁, … , w₁₉  opet su naznačene intenzitetom boje njihovih strelica).

­­

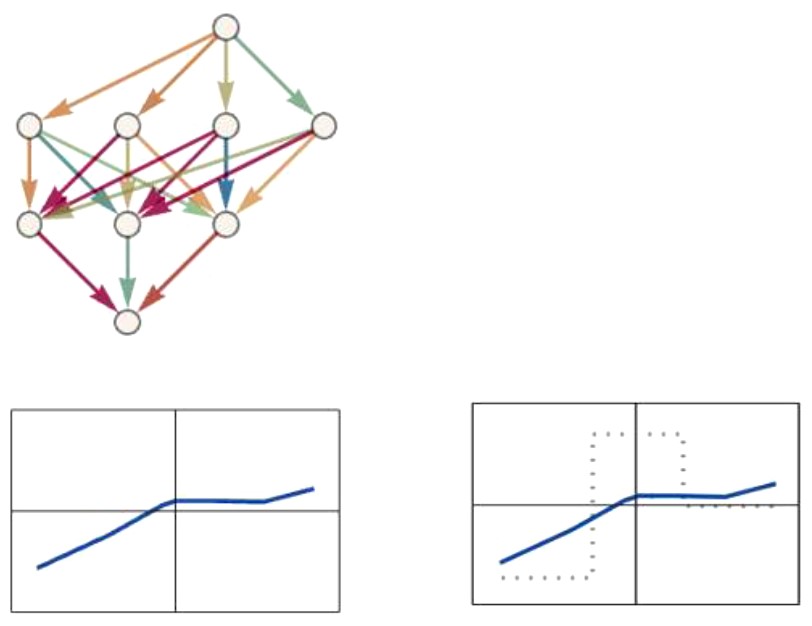
­Desno su zajedno ucrtani graf ciljane funkcije (crtkana linija) i graf funkcije koju neuralna mreža generira za odabrane težine w₁, … , w₁₉ (puna linija). Mjera pogreške je površina između ta dva grafa. To je tzv. funkcija gubitka G (w₁, … , w₁₉). Težine se dalje podešavaju tako da se w₁, … , w₁₉ promjene u w₁+ Δw₁ , … , w₁₉+ Δw₁₉, gdje su pomaci Δw₁ , … , Δw₁₉ oni koji daju najbrži pad funkcija gubitka G. I funkcija G (w₁, … , w₁₉) i pomaci koji osiguravaju njen najbrži pad (kada se pomičemo iz w₁, … , w₁₉) lako se nalaze standardnim metodama početnoga kursa integralnog i diferencijalnog računa funkcija više varijabli (a kako se to čini efikasno nalazimo u početnom kursu numeričke analize). Ponavljanjem tog postupka 1.000.000 odnosno 10.000.000 puta došli bismo do težina koje generiraju sljedeće funkcije.

­­

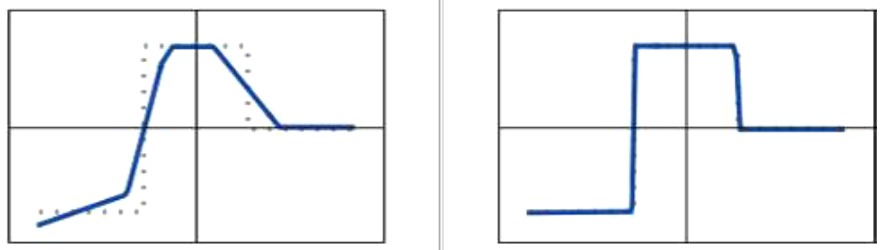
Veliki napredak u “dubokom učenju” zbio se 2010-ih kada je otkriveno da je lakše  minimizirati funkciju gubitka G s mnogo težina nego onu s malo. Drugim riječima, iako to možda nije očekivano, lakše je doći do optimalnih težina velikih neuronskih mreža nego malih. Razlog je taj što u prostorima s velikom dimenzijom n ima mnogo više smjerova (Δw₁ , … , Δw_n) u kojima se možemo pomicati iz točke (w₁ , … , w_n) nego što ih ima u prostorima s malom dimenzijom n (na 1-dim pravcu možete se pomicati samo „naprijed-natrag“, u 2-dim ravnini još i „lijevo-desno“, u 3-dim prostoru još i „gore-dole“, itd.). Taj veliki broj smjerova u prostorima velikih dimenzija lakše će nas dovesti do totalnog minimuma funkcije G (tj. do 0) dok ćemo s manjim brojem varijabli lakše zaglaviti u nekom lokalnom minimumu (koji nije 0) i iz kojeg više ne možemo izaći, jer iz minimuma naprosto nema “smjera najbržeg pada”.

Dodajmo da u tipičnim slučajevima postoji mnogo različitih razdioba težina koje neuronsku mrežu čine dobrim generatorom ciljane funkcije, tj. postoje različita rješenja zadanog problema. Zanimljivo ih je promatrati izvan zadanog područja analize (koje je u našem primjeru bilo interval [-1,1] i koje je „osvijetljeno“ na donjim grafovima ciljane funkcije). Ta rješenja izvan zadanog područja analize mogu biti veoma različita:

­­

Koje je ispravno? Nema načina da se odgovori na to pitanje. Sva su ona u skladu s podacima. No, razna bi rješenja mogla odgovarati različitim načinima razmišljanja o tim podacima izvan zadanih okvira. Na primjer, mreži koja je trenirana da razlikuje pse i mačke mogli bismo prikazati slike ljudi i ona bi ih klasificirala kao pse ili mačke. Ali razne mreže koje daju iste točne odgovore za pse i mačke davale bi različite odgovore za ljude (možda zato jer su njihove „ideje mačke i psa“ različite).

Važno je znati da je treniranje neuronskih mreža umijeće. U retrospektivi, katkada možemo naslutiti neko “teorijsko objašnjenje” uspješnosti utreniranih neuronskih mreža. Ali do njih se uglavnom dolazi metodom pokušaja i pogrešaka, uz mnogo trikova do kojih su došli majstori zanata. Kako oni to čine?

Prvo odabiru arhitekturu neuronske mreže koju kane trenirati za određeni zadatak. Netko bi mogao pomisliti da bi im za svaku vrstu zadatka trebala drugačija arhitektura. No, pokazalo se da za sasvim različite zadatke često funkcionira ista arhitektura. Osim toga, mislilo se da će trening biti lakši ako zadatak razbijemo na manje dijelove. Na primjer, u pretvorbi govora u tekst smatralo se da bi prvo audio zapis trebalo rastaviti na foneme pa provesti analizu na toj razini, zatim prijeći na razinu riječi pa na razinu sintagmi, rečenica itd. – malo po malo. Ali pokazalo se da je bolje neuronsku mrežu trenirati odmah na cijelom materijalu (dopuštajući joj da sama “otkrije” potrebne među korake). Postojala je i ideja uvođenja određenih algoritamskih procedura u rad mreže. Ali opet se pokazalo da to nije učinkovito. Umjesto toga, bolje je da se jednostavne komponente neuronske mreže “same organiziraju” i tako same dođu do ekvivalentnih algoritamskih procedura (to obično čine na način koji nažalost ne razumijemo).

Nakon što su se odlučili za određenu arhitekturu neuronske mreže, „neuronski inženjeri“ suočavaju se s problemom podataka za njeno treniranje. Često im je najveći izazov baš prikupljanje i priprema tih podataka. Naime, za trening želimo imati jasne primjere inputa i odgovarajućih outputa (npr. slike kao inpute i oznake što je na tim slikama kao outpute), a priprema takvog materijala (npr. prikupljanje slika i njihovo tagiranje) obično iziskuje veliki napor. Nije lako odrediti ni koliko podataka trebamo prikazati neuronskoj mreži da bismo je osposobili za određeni zadatak? Općenito, da bi se dobro istrenirale, neuronske mreže moraju “vidjeti“ mnogo primjera. Srećom, iskustvo je pokazalo da se primjeri mogu „u beskraj“ ponavljati pa je standardni trik zanata da se mreži iznova pokazuju isti primjeri. U svakoj od ovih “rundi treninga” (tzv. “epoha”) neuronska mreža će biti u nešto drugačijem stanju pa će je “podsjećanje” na određeni primjer natjerati da ga bolje “zapamti”. (Je li to analogno ljudskom „repetitio est mater studiorum“?) Naravno, stalno ponavljanje istog primjera ipak nije dovoljno; mreži je potrebno prikazati i mnoge varijacije. Srećom, pokazalo se da varijacije ne moraju biti sofisticirane da bi bile korisne (npr. samo neznatno obrađena slika može funkcionira kao nova; još jedan trik zanata).

Dakle, kako na kraju izgleda proces podučavanja neuronske mreže? Sve se svodi na  određivanje onih težina koje najbolje generiraju ciljanu funkciju (tj. onih koje najbolje predstavljaju primjere na kojima je mreža trenirana). To se postiže ranije opisanim postupkom minimiziranja funkciju gubitka . Ono što se obično dešava jest da funkcija gubitak pomalo pada i na kraju se stabilizira na nekoj konstantnoj vrijednosti. Ako je ta vrijednost blizu nule trening se smatra uspješnim. Ako nije, upali smo u neki lokalni minimum veći od nule i tada je najbolje pokušati s novom mrežnom arhitekturom.

Vratimo se konačno ChatGPT-u koji je i sam golema neuronska mreža. Arhitektura njegove mreže sadrži mnogo detalja koji su splet zanatskih trikova u koje ovdje ne možemo ulaziti. Osnovno je da sad već zastarjeli GPT-3 ima 175 milijardi veza s odgovarajućim težinama. Sjetimo se da mu je osnovni cilj da produži tekst na „razuman“ način, što znači na temelju primjera koje je „vidio“ u treningu. Sam trening je „pokazivanje“ tekstova s milijarda stranica na webu, iz knjiga i sl. Svaki input je komad teksta sa skrivenom sljedećom riječi, a output je baš ta skrivena riječ (priprema ulaznih podataka i njihovo tagiranje ovdje je bitno jednostavnije nego kod prepoznavanja slika). Težine se određuju na već opisani način.

Većina posla u treniranju ChatGPT-a troši se na “pokazivanje” enormno velikih količina tekstova, ali postoji još jedan vrlo važan dio. Čim završi “prvi trening” s tekstovima koji su mu prikazani, ChatGPT je spreman da (potaknut upitom) generira vlastite tekstove. No, iako se ti tekstovi često čine razumnima, oni ipak imaju tendenciju (osobito ako su dulji) da „odlutaju“ u smjeru „neljudskih“ tekstova (to nije nešto što se lako otkriva uobičajenim statističkim testovima, ali je nešto što stvarni ljudi lako primjećuju).

Zato je ključna ideja u konstrukciji ChatGPT-a bila napraviti još nešto nakon “prvog treninga”: omogućiti stvarnim ljudima da ChatGPT-u daju povratnu informaciju o tome koliko je dobar. Prvi korak je da ljudi ocijene rezultate koje mreža generira, a drugi je izgradnja nove neuronske mreže koja predviđa te ocjene. Tada se ta mreža pokreće (poput funkcije gubitka) na izvornoj mreži, što joj zapravo omogućava  da se “podesi” u skladu s „ljudskom“ povratnom informacijom. Taj dodatak ima veliki učinak na generiranje tekstova koji djeluju „ljudski“.

• Što možemo zaključiti ako se malo opustimo

Ljudski jezik oduvijek je smatran najvažnijom ljudskom karakteristikom. Mnogi dualisti čak drže nevjerojatnim da bi ljudski mozgovi sa 100 milijardi neurona i 100 trilijuna njihovih veza mogli biti jedini izvor mišljenja i jezika. Mora da postoji neki dodatni duhovni element koji je odgovoran za ta čuda. ChatGPT donosi važnu novu informaciju: čak i umjetna neuronska mreža (s približno onoliko neurona i veza koliko ih ima i ljudski mozak) obavlja iznenađujuće dobar posao generiranja nečeg što teško razlikujemo od ljudskog jezika. Možda to još nije jezik, još manje je mišljenje, ali jest nešto što iznenađuje, nešto što nismo očekivali.

Naravno, teško je povjerovati da se sve bogatstvo jezika, a pogotovo stvari o kojima on govori, može uklopiti u tako ograničen sustav. Dio onoga što se tu zbiva sigurno je odraz sveprisutnog fenomena da računalni procesi mogu dovesti do nevjerojatno složenih sustava čak i kada su njihova temeljna pravila krajnje jednostavna. Dovoljno je sjetiti se Conwayeve Game of life ili univerzalnog Turingovog stroja. Zato je sigurno važno razumjeti kako nešto poput ChatGPT-a može s jezikom dospjeti tako daleko. Možda će i tu odgovor biti da je jezik na temeljnoj razini jednostavniji nego što se čini. Možda je to razlog da u osnovi jednostavna struktura neuronske mreže može uspješno uhvatiti bar dio „biti ljudskog jezika“ (a možda i mišljenja koje mu je u pozadini). Time se otvara mogućnost postojanja nekih “zakona jezika” (a možda i “zakona mišljenja”) koje tek trebamo otkriti. U neuronskim mrežama (biološkim i umjetnim) ti su zakoni u najboljem slučaju implicitni i znanost stoji pred fundamentalnim zadatkom da ih učini eksplicitnima.

No, je li razumijevanje rada ChatGPT-a bar u nekom smislu i razumijevanje rada ljudskog mozga? U oba slučaja imamo strukturu neuronske mreže (uostalom, umjetna mreža modelirana je prema biološkoj) i neke od rezultata koje obje generiraju gotovo je nemoguće razlikovati. Ipak postoji velika razlika u hardwareu mozga i suvremenih računala, koja rezultira i mnogim drugim razlikama. Tu je i jedno specifično ograničenje ChatGPT-a. Za razliku od drugih programiranih sustava ChatGPT ne sadrži nikakve povratne veze ili jezikom matematike, ne sadrži rekurzije; daleko najjače oružje računalnih sustava. To nužno ograničava njegove računske sposobnosti čak i u odnosu na standardne računalne programe, a kamoli u odnosu na ljudski mozak. (Nije jasno kako povratne veze ugraditi u sustave poput ChatGPT-a i pritom zadržati jednostavnost njegovog treniranja.)

Uz sve te razlike, fascinantno je da ogroman broj krajnje jednostavnih računskih elemenata može generirati stvari koje ne možemo razlikovati od analognih stvari koje generira ljudski mozak. To ne znači da imamo vjeran model ljudskog mozga, ali sigurno imamo simplificiran i veoma poučan model.

Modeli su uvijek simplificirani i teško se direktno primjenjuju na realni svijet.  No, egzaktni matematički rezultati o tim simplificiranim modelima, mogu nam pokazati da su neke na prvi pogled nezamislive ideje ipak zamislive, pa možda čak i realne. Ti rezultati izgrađuju naše intuicije i tako nam pomažu da stvarnost počnemo gledati na novi način. Često na način koji nudi rješenja koja su jučer bila nezamisliva, a sutra se pokažu istinitima.