Moral i matematika. Treba li se oko aksioma usuglašavati? Što je realno, a što objektivno

Bilo bi to praktično dostignuće ako bi se svi složili da je Peti Euklidov postulat istinit, iznenađujuće zaključuje Justin Clarke-Doane, s obzirom na pretpostavku da su matematičke istine neovisne o nama. Čemu se onda o njima usuglašavati? Knjigu o odnosu matematike i morala, a ustvari o odnosu teorije i prakse, Željko Ivanković nastojao je ovdje predstaviti što jasnije

• Naslovna fotografija: Kurt  Gödel, kojeg autor Justin Clarke-Doane navodi kao “arhetipskog matematičkog realista”. (Flickr)

• Povezani prethodni članci: Matematika i filozofi. Koliko su matematički dokazi zaista egzaktni. Razumljivost; Moralna neizvjesnost. Matematika moralnih odluka

Justin Clarke-Doane, filozof sa Sveučilišta Columbia, autor studije Morality & Mathematics (Oxford University Press, 2020) doktorirao je s tezom pod istim naslovom desetak godina prije knjige, a u međuvremenu je pitanja iz istraživanja predstavio i u nizu znanstvenih članaka. Tako se to radi. Moral i matematika su na prvi pogled dva sasvim disparatna područja, dva svijeta. Matematika se sa svoje strane čini posve neovisnom o moralu; kaže se da je neutralna s obzirom na (moralne) vrijednosti, da je a-moralna (nije nužno ni moralna ni ne-moralna). Ako se pak unutar morala kalkulira, onda moral kao da nije pravi moral, kao da je nemoralan (unatoč utilitarizmu, ili upravo zbog njega). To njihovu usporedbu čini izazovnijom.

U knjizi su moral i matematika, te posebno njihov odnos, predstavljeni iz donekle neočekivane perspektive. Na samom početku, u odjeljku Znanost i vrijednost, autor ističe neku kao radnu hipotezu, koju provlači i testira kroz cijelu knjigu, a u kojoj tvrdi da: ne postoji principijelni temelj prema kojem bi netko bio matematički realist, a anti-realist kad je riječ o vrijednostima (str. 4); odnosno – tko god je moralni anti-realist na temelju epistemoloških razmatranja ima također biti matematički anti-realist (str.7).

Zaključci su, dakako, suprotni intuiciji prema kojoj su matematički činjenice realne, to jest – neovisne o nama i istinite, a moralne nisu (ako uopće postoje). Iako u filozofiji postoje i moralni realisti[i], matematički realizam izgleda jači: 2+2=4 što god mi mislili o tome. Realizam u filozofiji matematike vrlo je poznata i često razvijana pozicija koja se uobičajeno naziva platonizmom. Clarke-Doane od suvremenih navodi Kurta Gödela kao „arhetipskog matematičkog realista“ (str 21). Od početne teze ide i dalje. Tvrdi da empirijski znanstveni realist kao i naturalist u isti mah mora biti matematički realist: ako vjeruje u činjenice o genima, česticama itd., mora vjerovati u neovisne činjenice o brojevima, funkcijama itd. (str 3.) Ako je u filozofiji znanosti naturalist, ne može u filozofiji matematike biti formalist, fikcionalist, intuicionist… nego samo realist. Iako je studija fokusirana na usporedbu matematike i morala, na kraju ispadne da je značajna pažnja posvećena filozofiji i prirodi znanosti i svijetu iz znanstvene perspektive. Onaj tko bi knjigu čitao samo iz tog kuta imao bi puno materijala za raspravu.

Knjiga započinje raspravom o realizmu/platonizmu nekog područja, što to znači i dalekosežnim tezama o realizmu matematike i morala. Naslovnica i autor Justin Clarke-Doane (Columbia University)

U mnoštvu zaključaka dva se mogu smatrati najvažnijima i donekle su isprepleteni (kao i štošta u knjizi). Prvi je ‘primat prakse’, a drugi zaključak govori o objektivnosti morala. Jedna je od uobičajenih predodžbi da je matematika objektivna a moral subjektivan. Stoga matematika nužno ide prema jednoglasju a moral ne može izbjeći višeglasje. Autor međutim inzistira na pluralizmu u matematici, koji doduše ne sprečava suglasje ali je drukčiji od moralnog pluralizma. S tom je razlikom dvaju pluralizama povezana specifična definicija/identifikacija objektivnosti koja je „u napetosti prema realizmu“. Clarke-Doane napominje da je  svjestan da se realizam i objektivnost često poistovjećuju. Prema tom razumijevanju moralna pitanja su objektivna (a matematička nisu) zato što teorijski odgovor na njih ne rješava praktički problem: što učiniti?

• Primat prakse

Što se dakle tiče teorije-prakse, od Antike se matematiku uzima kao najizrazitiji primjer teorije, a moral (i politika) egzemplarni su za praksu. (U nijanse, kao i u prirodu tehnike i umjetnosti s obzirom na razliku teorije i prakse ovdje je suvišno ulaziti.) Clarke-Doane je eksplicitan: „Praktična filozofija treba, dakle, zauzeti centralnu poziciju“ (str. 12)  a naslov posljednjeg odjeljka u knjizi je: Prema praktičnoj filozofiji! To se u Antici, a posebno u klasičnom njemačkom idealizmu nazivalo primatom prakse. I Wittgensteinov pomak od slike (Tractatus) prema igri (Filozofska istraživanja), može se tumačiti da ide od kontemplacije prema praksi. Riječ je naravno o grubom poopćavanju jer su slika svijeta, argumenti i njihov slijed a također i pojmovi prakse i teorije u Antici drukčiji nego poslije u Novom vijeku i posebno u Klasičnom njemačkom idealizmu ili kod Wittgensteina. Svejedno je intrigantno pitanje kako je rezoniranjem analitičkog filozofa izvedena ‘kontinentalna’ konkluzija? Ima li nešto u tome što stvar opet završava isto?

Prije predstavljanja poglavlja i završnog osvrta na studiju – dvije digresije. Prva. U nekim je opservacijama jasno izražavanje ključna prednost analitičke pred kontinentalnom filozofijom. Morality & Mathematics tu navodnu prednost dovodi u pitanje. Poplavi citata, imena, i tehničkih termina u knjizi nije se lako othrvati. Naravno, studija je jasnija onome tko bolje poznaje suvremene filozofiju matematike i morala, ali i zagovornici kontinentalne filozofije tvrde da je Hegel jasniji onima koji bolje poznaju njemački idealizam i tradiciju iz koje se razvio nego onima koji u njega uskoče nepripremljeni. Već u prvom paragrafu Clarke-Doane navodi gotovo kao svoj moto da je zadaća filozofije uvid u to kako su stvari međusobno povezane ali gledajući s razine cjeline (a nasuprot sveprisutnoj specijalizaciji koja se čak i u filozofiji zna smatrati napretkom). Kolikogod međutim sam nastojao dovesti analizu do nekog općeg zaključka, do neke svodne ideje, nije uspio raščistiti drveće koje odvraća od pogleda na šumu. Da jest, bio bi jasniji. Problem je možda u tome što autor od početka pa kroz veliki dio knjige inzistira na spomenutim sličnostima matematike i morala. Na kraju ta područja razlikuje i individualizira, ali na svoj način – tako da uvodi drukčije shvaćanje pluralizma i objektivnosti u područjima matematike i morala.

Onaj tko bi knjigu ocijenio kao nesuvislo i teško prohodno smeće (što se uostalom može pročitati i o Hegelu) ne bi nužno bio zlonamjeran – zbog kaotične argumentacije, pompoznog stila, stalnog naglašavanja zaključaka, kao da uz svaki dodaje uskličnik i napornog neprestanog uzbuđenja autora.  Ali, za sigurnost takve tvrdnje potrebno je potrošiti neko vrijeme, a nitko nije sklon smatrati ga bačenim. U nastojanju da se pronikne u cjelinu, odnosno kakve veze što ima s čime, iz nabacanog se materijala, koji omogućava (pre)širok spektar tumačenja, ipak može izvesti neka razmjerno razumna interpretacija (to se dogodilo i Hegelu). Zašto ne? S nešto sreće, interpretacije mogu popraviti izvornik, čak i obogatiti. U njega je zaista uložen golem trud. Paradoksalno, studija bi možda čak mogla biti korisna da u nekom filozofskom seminaru zainteresirani sudionici prođu kroz selekcioniranu seriju tema suvremene analitičke filozofije koje Clarke-Doane nije naravno sve produbio ali je u većini ambiciozan (dakako uz konzultiranje i druge literature). Studenti se mogu upoznati i s načinom pisanja koji nije rijedak a bolje ga izbjegavati.

Druga digresija. Konkluziju o ‘primatu prakse’ bolje je nazvati tradicionalnom nego kontinentalnom, prvo – zato što u onom što se naziva kontinentalnom filozofijom ima puno filozofa uz koje se primat prakse ne može vezati, a zatim i zato što ‘primata prakse’ ima u filozofskoj tradiciji koja nije u užem smislu riječi ‘kontinentalna’. Kad na kraju knjige objašnjava taj svoj zaključak Clarke-Doane upućuje na sličnost s Humeovom lapidarnom, ali često diskutiranom is-ought distinkcijom prema kojoj se u onome što jest (dakle u realistično shvaćenoj matematici) i u onome što treba (moralu), slijede „različite logike“[ii]. Hume nije rijetka inspiracija u dominantno anglosaksonskoj analitičkoj filozofiji, iako je njegova distinkcija inspiracija i u ‘kontinentalnom’ njemačkom idealizmu.

Kad na kraju knjige pokušava objasniti svoj zaključak autor upućuje na lapidarnu is-ought distinkciju. David Hume (Wikimedia Commons)

Od ‘tradicionalnih’ filozofa autor citira i Lockea, u poglavlju o dokazu i o onome što je očito (self-evident), te neizbježnog Platona koji je „blisko povezao“, piše Clarke-Doane, matematičke forme i pojam dobra (u pitagorejskoj tradiciji, u knjizi 7 Republike, u kojoj je i čuvena alegorija spilje). Pronašao je i iznenađujuće veliki broj citata suvremenih filozofa o odnosu  matematike i morala. Uz ostale diskutira teze analitičkih autoriteta kao što su Quine, Putnam, Kripke, Lewis, Moore …, zatim filozofa morala (Parfit, Nagel, Dworkin, Singer…), a među filozofima matematike posebno su mu važni Benacerraf i Field. Puno je pažnje posvetio diskusijama svojih očito bližih kolega nakon 2010. godine. Ispada da filozofiranje o odnosu matematike i morala uopće nije rijetko. To osnažuje pretpostavku da interpretacija ideja iz ove knjige može biti vrijedna. Uostalom, filozofija nije poput drugih znanja i sposobnosti, nije prvenstvo. Vrijedne se ideje mogu zateći i kod najkonfuznijih. Važne su ideje. Zato, sad slijedi sadržaj poglavlja, zaključci autora, te još neka zapažanja koja izgledaju zanimljiva.

U prvom poglavlju Clarke-Doane se bavi realizmom nekog područja. Prema jednoj radnoj definiciji moral su norme ponašanja[iii]. Norme ponašanja su međutim i zakoni i običaji, religije imaju ritualne i ceremonijalne norme neovisne o moralnim normama, a pravila ponašanja nameće i etiketa (manire, zahtjevi pristojnosti). Nije lako odgovoriti što su baš moralne norme, moralno područje, neovisno o razlici prema ostalim spomenutim područjima? Uz to, pojam moralnosti može se koristiti u deskriptivnom smislu, kad se opisuju norme u pojedinoj sredini, te normativno, kad se odstupanja od normi (ili druge norme) smatraju nemoralnima. Recimo, bogaćenje: može se smatrati moralno poželjnim, može se smatrati ni moralnim ni nemoralnim (ljudi kažu -‘ovisi’) ili se može uzeti kao nemoralno po sebi. Ako se dakle pojam moralnosti ne koristi deskriptivno (koje norme vladaju u nekoj sredini), nego normativno, onda bogaćenje u posljednjem slučaju ne potpada pod moral (a ni u pretposljednjem). Kako je svjestan da je područje morala vrlo neodređeno, Clarke-Doane primjenjuje misaoni trik, rekao bih karakterističan za analitičke filozofe. Umjesto da se izravno bavi pitanjem realizma u matematici i moralu, pribjegava opisu kriterija na osnovi kojih se može govoriti o realizmu nekog područja F. Jedan recenzent knjige ističe da se Clarke-Doane bavi meta-etikom[iv].

Kriteriji za realizam su ponajprije već spomenuto istinito vjerovanje o činjenicama neovisnima o jeziku i našim razmišljanjima, iako Clarke Doane detaljizira još neke. Tu uvodi svoje određenje objektivnosti, koje postaje jasnije tek u završnom poglavlju u kojem izvodi konačni zaključak studije da su moralna pitanja, za razliku od matematičkih, objektivna jer su praktična i jer zahtijevaju da se na njih da samo jedan odgovor. Čak i kad je u pitanju trolley problem koji pita: žrtvovati pet života koja su na putu vlaku ili jedan život koji je sa strane, na sporednom kolosijeku (i – recimo – nije umiješan u slučaj)? Tek na kraju postaje jasno da se u cijeloj knjizi ispituje realnost matematičkih i moralnih vjerovanja (beliefs), odnosno tvrdnji, koje pripadaju u teorijsko znanje, a da se zaključak izvodi o objektivnosti odgovora na praktično pitanje. Clarke-Doane to ne formulira tako, ali po mojem razumijevanju tu, u praksi, radi se o neizbježnosti odluke.

• Ovisnost matematike o okolnostima

Iz ovog poglavlja vrijedi zabilježiti zanimljivo, a rekao bih i dalekosežno zapažanje o određenju područja matematike i morala. Povjesničari će, piše autor, uočiti da su se prakse vrednovanja (evaluative practices) s vremenom mijenjale i da je teško vjerovati da postoji magični moment u kojem su postale ‘moralne’. (str. 14). Iako matematički predikati izgledaju određenije, koncept matematike se od Antike također mijenjao (str.15). Taj točan zaključak odskače od uobičajene predodžbe o matematici, čija se povijest uostalom u nastavi vrlo rijetko poučava. Toj se temi Clarke-Doane vraća i u poglavlju 5. u kojem raspravlja o pouzdanosti (reliability) matematike i morala. Zaključuje da je povijest matematike mogla biti i drukčija, recimo da je Aksiom determinacije uveden prvi, prije Aksioma izbora. „Zamislite“, citira Pavela Pudláka, „da se tad netko pojavio s Aksiomom izbora i dokazao paradoksalne konzekvence. Ne bi li situacija bila obrnuta u smislu da bi Aksiom determiniranosti bio ‘pravi aksiom’ a Aksiom izbora tek bizarna alternativa.“ (str. 150). Striktno govoreći, zaključuje Clarke-Doane, Pudlák samo poentira na onome što je neupitno, da bi matematička zajednica imala drukčija vjerovanja o teoriji skupova (set-theoretic beliefs) da je povijest išla drugim tokom (str. 150).

Norman Wildberger, profesor matematike sa sveučilišta New South Wales, smatra da je povijest matematike i trebala biti drukčija, da se trebala razvijati u drugom smjeru, prema izračunljivosti (computability). Wildberger dovodi u pitanje realne brojeve, Dedekindov rez, i novovjeki pojam beskonačnosti za razliku od antičkog (i azijskog). Poznato je da u matematici nema čudaka, ni oni koji izgledaju kao čudaci nisu čudaci, nego ih se uvijek ozbiljno razmatra, barem donekle. U drugom  poglavlju, u odjeljku o uvjerljivosti i neslaganju (Plausability and disagreement) Clarke Doane spominje da su neki matematičari „išli toliko daleko da su doveli u pitanje postojanje 2¹⁰⁰ “.

Predodžba o tome da je moral određen socijalnim okruženjem a matematika nije, komplementarna je pitanju o povijesnosti tih dvaju područja. Clarke-Doane na kraju poglavlja 2. ističe da na odnos prema temeljnim (i neupitnim) matematičkim istinama znatno utječe obrazovanje (str. 61),  a zatim pokušava okrenuti pilu naopako: Prihvatimo, kaže, tezu da je moral za razliku od matematike odrežen socijalnim okruženjem. To apriorno opravdanje moralnih vjerovanja čini čak snažnijim od apriornog opravdanja matematičkih vjerovanja jer su se moralna vjerovanja za svoju apriornu neupitnost izborila probijajući se kroz socijalna iskrivljenja (str 62.). Ne čini se produktivnim puno raspravljati s tom vrstom misaonih obrata, kojih u knjizi itekako ima. Tezi o ovisnosti matematike i morala o socijalnim i povijesnim okolnostima sukladan je pluralizam u oba ta područja, koji je temelj autorova izvoda (i glavna tema poglavlja 6.). Međutim, Hallvard Lillehammer u recenziji knjige [v] prigovara da Clarke-Doane ne respektira pluralizam na kojem toliko inzistira. Puno autorovih zaključaka, piše  Lillehammer,  ovisi o tome kako su područja definirana (individuated). Clarke-Doane ispušta primijenjenu i ‘nečistu’ matematiku, a (po vlastitim riječima) istražuje ‘čistu’, iz koje može braniti svoje teze. I koja je, podsjetimo, mogla biti drukčija. Od kraja  19. a posebno u 20. stoljeću veliki dio matematičkih istraživanja zaista se kreće u spekulativnom, da ne kažemo – filozofskom području.

S uspostavom i razvojem Riemannove geometrije Euklidova geometrija nije postala lažnom, inzistira Clarke-Doane. Bernhard Riemann (Wikimedia Commons)

U poglavlju 2 autor dokazuje da se ne može reći da su matematička vjerovanja (o realnim matematičkim činjenicama) a priori opravdanija nego moralna vjerovanja, a u poglavlju 3 da se ne može reći da su matematička vjerovanja empirijski opravdanija nego moralna vjerovanja. Ta dva poglavlja izgledaju manje kao istraživanje morala nego kao filozofsko seciranje matematike i boljem poznavatelju vjerojatno ne donose ništa neočekivano[vi]. Čuvenoj apriornoj istini da je 2+2=4 autor suprotstavlja apriornu moralnu istinu da je ubojstvo nevine djece zlo. Matematika dakle nije u prednosti kad se radi o tim ‘atomskim vjerovanjima’. Pretpostavlja se da je ipak u prednosti kad je riječ o dokazivanju matematičkih teorema iz aksioma. Clarke-Doane prvo pokazuje da aksiomi (suvremene matematike) ni izbliza nisu tako očigledni, a čak kad se čini i da jesu, u matematici o njima postoje ozbiljna sporenja. Slično je i s tradicionalnim aksiomima, recimo s Petim Euklidovim postulatom, postulatom o paralelnim pravcima, koji je autorov glavni primjer, a koji govori da se kroz točku izvan pravca može povući samo jedan paralelni pravac, koji se s danim pravcem nigdje ne siječe nego paralelno idu u beskonačnost. (Euklidova formulacija je nešto kompleksnija i možda čak nije toliko ‘očigledna’.)

Iz Euklidovih aksioma, uključujući i Peti, nužno slijede geometrijski zaključci, recimo da je zbroj kutova u trokutu 180 stupnjeva. S uspostavom i razvojem Riemannove geometrije, kojom se fizičari koriste u teoriji relativnosti, Euklidova geometrija, kao čista matematička teorija nije, piše Clarke-Doane, proglašena lažnom (str. 82). Sjetimo se, neovisna i istinita vjerovanja preduvjeti su realizma u matematici. Euklidova i Riemannova geometrija su samo drukčije. Naravno, ne postoje ‘moralni aksiomi’, piše Clarke-Doane, postoje moralni principi, ali uvijek ih je moguće uzeti i iz njih dokazati ‘moralne teoreme’ (str.41). Taj paralelizam je upitan. Bilo bi zanimljivo da je Clarke-Doane pokušao iz moralnih principa dokazati moralne teoreme e da se vidi koji se problemi otvaraju. Umjesto toga, kao argument on citira Lockea: „Ako ih se pažljivo razmotri i slijedi (moralne propozicije) omogućavaju takvo utemeljenje naših dužnosti i pravila postupanja da to pozicionira moralnost među znanosti u kojima je moguć dokaz (sciences capable of demonstration). … ‘Gdje nema vlasništva nema nepravde’, tvrdnja je toliko pouzdana kao bilo koji Euklidov dokaz.“ (str. 41, bilješka 8). Rasprava o dokazu više ‘demistificira’ dokaz u matematici nego što afirmira nekovrsni dokaz u moralu i teoriji morala.

Dok elektroni, geni itd. imaju neku kauzalnu ulogu u prirodnim zbivanjima, za matematičke to nije moguće ustanoviti. Broj 12 nema kauzalne veze ni s čim, kauzalno je inertan.

U poglavlju 3 argumentira se da matematička vjerovanja nisu empirijski opravdanija nego moralna. Znanstvenici se, glasi teza, kad objašnjavaju opservacije koje podupiru njihovu teoriju tipično pozivaju na matematičke principe a nikad na moralne (str. 67). Prije spomenutu tezu prema kojoj empirijski znanstveni realist (onaj koji vjeruje u neovisne činjenice o genima, elektronima itd.) mora biti matematički realist (vjerovati u neovisne brojeve itd.), valja razlikovati od komplementarne teze iz ovog poglavlja, da je  empirijska znanost, od fizike do ekonomije, „do ušiju“ u matematici (str. 69). Naravno, veliki dijelovi matematike nemaju veze s empirijom. A tu je i problem tzv kauzalne inertnosti (realnih) moralnih i matematičkih pojmova. Po toj ‘apstraktnosti’ matematika i moral su slični. Dok prije spomenuti znanstveni entiteti (elektroni, geni) imaju neku kauzalnu ulogu u prirodnim zbivanjima, za matematičke to nije moguće ustanoviti. Broj 12 nema kauzalne veze ni s čim. Kauzalna inertnost matematičkih činjenica je jedna od najmanje kontroverznih u filozofiji, piše Clarke-Doane, i iako je izazvala razvoj fikcionalizma, s njome se slažu i matematički realisti. Platonistički entiteti (matematički ili moralni) po pretpostavci su izvan vremena i prostora i ne mogu biti dio kauzalnih relacija. Autor čak zaključuje da je kauzalna inertnost uvjerljivija u matematici nego u moralu (str 71-75).

Previše je teza u ovom poglavlju e da bi se svaku samo spomenulo a kamoli diskutiralo. Iako su nekako povezane s problemom od kojeg je autor započeo, teško ih je uklopiti u cjelinu i konačni zaključak. Tako tezu Hartryja Fielda o mogućnosti  ‘znanosti bez brojeva’ spominje tek kao jednu od bizarnih i samo da bi se njome suprotstavio nekoj drugoj, a ne da bi je pozicionirao u prije spomenuta razmatranja odnosa matematike i prirodnih znanosti (str. 81). Ne bi li pokazao da je moral čak bliži empiriji nego matematika upustio se u kompliciranu raspravu o percepciji, kvazi-percepciji i intuiciji (str 84-88). Pitanje najboljeg objašnjenja, kad je riječ o odnosu matematike ili morala s empirijom, kao i svaki drugi odjeljak poglavlja 3, mogu biti posebna tema u nekom filozofskom seminaru. Brian Leiter u svojem se osvrtu (bilješka iv) fokusirao na ovo poglavlje i korisno raščlanio neke ovdje nespomenute teze.

Moralne norme su ishod evolucije. Charles Darwin (Wikimedia Commons) i njegovo Podrijetlo čovjeka

Poglavlje 4. nosi naslov Genealogy Debunking Argument, a time se ustvari bavi i 5. poglavlje. Radi se zapravo o tezi da su moralne norme ishod evolucije[vii], dakle moralni sud (ropstvo je zlo) nije i ne mora biti istinit i neovisan kako pretpostavlja moralni realizam (str. 100). Matematičke istine (2+2=4) imaju drukčiji status. Upravo zato što su istinite  one podižu reproduktivnu sposobnost (str 102).  Kao ilustraciju prenijet ćemo citat samog Darwina (iz Podrijetlo čovjeka) kako ga navodi Clarke-Doane (str. 108):

Na isti način na koji različite životinje imaju neki osjećaj za lijepo, unatoč tome što obožavaju vrlo različite predmete, tako mogu imati osjećaj za ispravno i pogrešno (right and wrong), premda vođeni njime slijede različite linije postupanja. Da su se, na primjer … ljudi razvili (reared) pod precizno istim uvjetima kao pčele iz košnice, teško je posumnjati da neudane žene, poput pčela-radilica, ne bi ubojstvo braće smatrale svetom dužnošću a majke bi nastojale ubiti svoje plodne kćeri i nitko ne bi razmišljao o tome da se umiješa. Stoga bi pčela, ili bilo koja druga životinja, u našem pretpostavljenom slučaju stekla … određeni osjećaj za ispravno i pogrešno, ili savjest.

Radi se o složenoj i intenzivnoj diskusiji o kojoj je ionako ogromna literatura u posljednje vrijeme samo rasla, a među laicima je popularna zajedno s jednako čestim pitanjem slobode volje. To što joj Clarke-Doane posvećuje dva poglavlja osnažuje zaključak da se knjiga može čitati i kao filozofija o znanosti. Tezi pristupa iz specifičnog epistemološkog kuta[viii]. Kako evolucija razvija reproduktivnu sposobnost to moralne norme mogu biti istinite (ili ‘ispravne’?) samo slučajno. Analizira epistemološke karakteristike tih ‘slučajnih’ normi i matematičkih istina: koliko su vjerojatne, koliko su pouzdane, koliko su senzitivne na pogrešku, koliko se lako mogu uspostaviti neke druge. Clarke-Doane tvrdi da je tezu uglavnom opovrgnuo (str 119 i poslije), no rasprava o njoj  i njegovom pristupu temi zahtijeva poseban članak.

Euklidova i Riemannova geometrija su obje istinite jer su obje konzistentne. Može li međutim u isto vrijeme biti istinit i Peti Euklidov postulat i njegova negacija. Ili u tom slučaju – prolazi sve

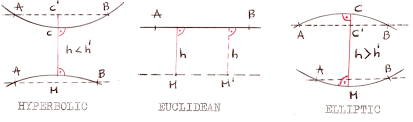
Nakon cijele odiseje u poglavljima 2 – 5, u poglavlju 6. naslovljenom Realism, Objectivity and Evaluation autor se vraća pitanjima s početka. Glavna je tema ustvari pluralizam i to prvo matematički. Glavni su primjeri Peti postulat odnosno Euklidova i Riemannova geometrija kojima su, u onome što zanima autora, analogne sve druge matematičke ‘konstrukcije’ različitih svjetova. Euklidova i Riemannova geometrija su realne, dakle istinite i neovisne o našem mišljenju i jeziku, prije svega zato što su konzistentne. Može se prihvatiti, no te dvije geometrije su konzistentne na isti način, u objema se slijedi ‘ista logika’, pripadaju dakle jednom logičkom svijetu u kojem treba prihvatiti da su istiniti oboje: Peti postulat i njegova negacija (odnosno varijanta u Riemannovoj geometriji prema kojoj se kroz točku izvan pravca ne može provući nijedan paralelni pravac, nijedan a da se dakle ne siječe s danim pravcem). Je li to moguće? Prihvati li se da su istiniti i Peti postulat i njegova negacija onda se prihvaća sve, anything goes (str 158 i dalje).

Matematički pluralizam je pogled prema kojem je svaka (moj kurziv) konzistentna matematička teorija o nekom predmetu istinita neovisno o čovjekovom umu i jeziku (str. 160), piše Clarke-Doane i referira se na niz autora. Matematičari, a ni autor knjige, ustvari u toj matematici ne vide problem (naprotiv). Pouzdanost (reliability) nekog vjerovanja, tvrdnje, teorije, u epistemologiji koju opisuje Clarke-Doane, ovisi o tome možemo li ih steći (pre)lako (safety), i koliko su osjetljivi (sensitivity) na laž, je li im prepoznatljiva. Kolokvijalno rečeno, koliko se lako možemo zaribati. Koliko god, međutim, argumentirali da ne možemo lako (easily) imati lažna matematička vjerovanja (i ona ‘analogna’ matematičkima, mathematical-like) jednako možemo argumentirati za intuitivno suprotan zaključak, da se lako možemo zaribati, uočava Clarke-Doane (str. 161).

Iz problema se nastoji izvući uvodeći pojam aritmetičke pouzdanosti (soundness), kojim uz konzistentnost i ostale kriterije zahtijeva konačnost (finiteness) teorije, a slijedom kojeg aritmetički uvjerljiva teorija ne implicira lažne rečenice, što omogućava njezinu koherentnost. Vrlo apstraktno. Ne izgleda kao baš neki izlaz. O čemu je približno riječ saznaje se gotovo ovlaš u sljedećim paragrafima. Prvo, važna je elaboriranost ‘alternativnih’ matematičkih teorija, recimo Riemannove geometrije, a drugo – Clarke Doane upućuje na – uspjeh znanstvenika u njihovoj primjeni (str. 162).

Autor ne misli da su moralni entiteti realni, nego samo da se argumente za njihovu nerealnost može primijeniti i na matematiku, a argumente za realizam matematike može primijeniti i na moral

S moralnim pluralizmom Clarke-Doane je na još tanjem ledu. Podsjeća na zapažanje s početka knjige, kojim se u međuvremenu uopće nije bavio, prema kojem matematičke tvrdnje, na primjer ‘2 je prosti broj’, govore o izvanprostornovremenskim entitetima, a moralni se predikati ipak odnose na akcije ili ljude (recimo: Napoleon je bio zao). Utoliko je moralni pluralizam ‘metafizički’ trivijalan, piše. Ni moralni predikati (‘zao’, ili ‘maksimizacija koristi’), epistemološki nisu sporni više nego predikat ‘je restoran’ (npr. u tvrdnji – ona zgrada ‘je restoran’)[ix]. Moralni pluralizam je, međutim, u odnosu na matematički, nezadovoljavajući jer se od morala očekuje da nam kaže – što raditi?! (str 164) S moralom se ne može izmotavati kao s matematikom, moral je praktičan.

Ako je čitatelj zbunjen zaključkom da se moralni predikati odnose na stvarne ljude i akcije, da dakle nisu neovisni o nama (nisu realni) niti su u istom izvanprostornovremenskom području kao matematički, valja napomenuti da ovo razmišljanje ne dovodi u pitanje na početku spomenutu autorovu tezu prema kojoj argumenti za moralni anti-realizam opovrgavaju i matematički realizam, a argumenti za matematički realizam vrijede i afirmiraju i moralni realizam[x]. Ne misli da su moralni entiteti realni, nego samo da se argumente za njihovu nerealnost može primijeniti i na matematiku. Teze dakle logički mogu biti zadovoljene i u slučaju anti-realizma obaju područja. Tim riječima završava Leitner svoj osvrt (bilješka vi) uz dodatak da ne misli da bi autor knjige time bio zadovoljan. No, možda i bi, kao što ćemo uskoro vidjeti.

Clarke-Doane zatim na nekoliko stranica dokazuje da se u slučaju moralnog pluralizma ne radi o različitim značenjima pojma ‘dobro’ u različitim sredinama i sustavima, nego, implicite, upravo o razlikama između maksimalne koristi, dobra, prava, pravednosti, jednakosti itd. kao moralnih načela (njegova terminologija je drukčija). Iz nekog se moralnog obzora može zaključiti o moralnosti nekog postupka a da se time ne upućuje da to treba učiniti[xi]. Kroz cijelu je knjigu nastojao, piše, ukazati na sličnosti matematike i morala, no dok matematički pluralizam odgovara na matematičko pitanje, moralni pluralizam ne odgovara. Kad kažemo što ‘treba učiniti’ uopće ne govorimo o nekom atributu, o nekoj karakteristici. Tu upućuje na Humeove „različite logike“. No kako možemo učiniti samo jednu stvar to ne možemo ni pomisliti da nismo objektivni. Napokon, Clarke-Doane zaključuje: Matematika je teorijska, moralnost je praktična (str 171).

Karl Popper kritizirao je ‘platonizam logičkih formi’ u analitičkoj filozofiji i tendenciju izražavanja formaliziranim znanstvenim jezikom. Clarke-Doane svjestan je ograničenja platonizma, ali se pogubio u tendenciji prema formulaičnosti.

Naslovna tema knjige je fantastična. Clarke-Doane je pokazao da su je više ili manje eksplicitno, dotaknuli mnogi filozofi, ali nikad detaljno. Na brzu ju je ruku povezao s cijelom serijom recentnih pitanja u suvremenoj analitičkoj filozofiji, od kojih je ovdje pragmatično preskočena čak većina. Ako bi čitao ovaj prikaz vjerojatno bi sam na njih pokušao skrenuti pažnju. Kolikogod mu se u nekoj njegovoj slici cjeline možda činila i nezaobilaznima, uglavnom ih je elaborirao prebrzo kao i razliku matematičkih i moralnih tvrdnji koje su o ljudima i akcijama, a kojima se morao vratiti jer se u toj razlici dijelom očituje razlika teorije i prakse, što je u pozadini svih njegovih analiza.

Clarke-Doane vjeruje da njegova analiza morala i matematike „može biti od općeg interesa“ jer postoje područja (filozofskog istraživanja) slična moralu, kao što su normativna epistemologija i prudencijalno rezoniranje, i ona koja su sličnija matematici, kao što su modalna metafizika i ne-normativna logika (str. 8). Očito je ispitujući sličnosti i razlike morala i matematike zapravo ispitivao sličnosti i razlike teorije i prakse. Ne izgleda da je u njihovoj karakterizaciji i u bazičnoj karakterizaciji morala i matematike, kojima se na kraju morao vratiti, načinio veliki napredak. Kad se vraća ambiciji poopćenja nalaza, ponavlja da praktička pitanja ne mogu biti riješena na isti način kao teorijska:

Bilo bi to praktično dostignuće, piše, ako bi se svi složili da je Peti postulat istinit (str. 182). Radikalan zaključak, no uklapa se u spomenutu povijesnost matematike, iako je pitanje kako sad stvari stoje s matematičkim realizmom koji zahtijeva da je istinitost matematike neovisna o nama.

Znanost, koja je dakle snažna podtema knjige, obično se poput matematike smatra moralno neutralnom. Clarke-Doane oscilira oko njihova odnosa. Kao i mnoge druge teme tek je natuknuo da se epistemološki problemi matematičkog pluralizma (Euklidska i Riemannova geometrija) rješavaju u znanstvenoj primjeni. Iako se često uvrštava u teoriju, znanost je slijedom tog zaključka praktična, traži odgovore, objektivna je, rekao bi Clarke-Doane[xii]. To sobom nosi neizvjesnost kao karakteristiku prakse (izvedbe). Kako je pak u praksu znanosti uključen vrijednosni sadržaj stvar je daljnjeg istraživanja, dijelom nesumnjivo i empirijskog. Tu bi se mogao kriti odgovor na pitanje zašto je i usporedba matematike i morala u okviru analitičke filozofije završila primatom prakse.

U engleskom izdanju svoje knjige Logika znanstvenog istraživanja iz 1959. godine, Karl Popper kritizira ‘platonizam logičkih formi’ vidljiv u analitičkoj filozofiji te tendenciju da se izražava formaliziranim znanstvenim jezikom[xiii]. Clarke-Doane i sam vidi ograničenja tog platonizma, ali se u tendenciji prema formulaičnosti prilično pogubio[xiv]. Stvar je interpretatora zainteresiranih za usporedbu morala i matematike da pokušaju iskopati i oblikovati materijal koji smatraju značajnim.

• Bilješke

[i] Sayre-McCord Geoff,  Moral Realism, The Stanford Encyclopedia of Philosophy (Summer 2021 Edition), Edward N. Zalta (ed.) URL = https://plato.stanford.edu/archives/sum2021/entries/moral-realism/

[ii] Upućujem na barem dva izvora: Wiley, James, 2012, Theory and Practice in the Philosophy of David Hume, Palgrave Macillan; The Is-Ought Question, edited by W. D. Hudson, Macmillan Education, 1969.

[iii] Gert, Bernard and Joshua Gert, “The Definition of Morality”, The Stanford Encyclopedia of Philosophy (Fall 2020 Edition), Edward N. Zalta (ed.), URL = https://plato.stanford.edu/archives/fall2020/entries/morality-definition/

[iv] Leiter, Brian, 2021: Realism, Disagreement and Explanation, Philosophy & Phenomenological Research, URL https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3906745

[v] Lillehammer, Hallvard: Review of Justin Clarke-Doane, Morality & Mathematics, International Journal for the Study of Skepticism. URL https://philpapers.org/rec/LILROJ

[vi] Clarke-Doane ih sintetizira u članku Moral Epistemology: The Mathematics Analogy, Noûs, 48:2 (2014), 238-255

[vii] Za sintezu te teme vidi: FitzPatrick, William, “Morality and Evolutionary Biology”, The Stanford Encyclopedia of Philosophy (Spring 2021 Edition), Edward N. Zalta (ed.), URL = https://plato.stanford.edu/archives/spr2021/entries/morality-biology/

[viii] Ponovo, svoj je pogled sintetizirao u posebnom članku:  Clarke-Doane, Justin (2012) Morality and Mathematics: The Evolutionary Challenge Author, Ethics , Vol. 122, No. 2, pp. 313-340 Published by: The University of Chicago Press Stable URL: https://www.jstor.org/stable/10.1086/663231

[ix] Ovdje možda treba podsjetiti na Mooreov Open Question Argument, kad su predikati – nesvodivi. Na primjer, ako se kaže – ‘užitak je vrhunsko dobro’ ili ‘korisnost je ključno dobro’ ostaje pitanje – što je dobro (po sebi, rekli bi filozofi, da naglase). Kod restorana je s time lakše izići nakraj nego kod pojma dobro, ali Clarke-Doane je tu diskusiju preskočio.

[x] To je često i vrlo iritantno među filozofima, taj pristup: ne tvrdim A, nego samo da nije ne-A. Recimo, ne tvrdim da je netko kriminalac, nego samo da argument kojim se opovrgava da je kriminalac ne znači da zaista nije kriminalac. Zaista, ako netko nije ukrao jabuku to još ne znači da nije kriminalac, da nije ukrao bicikl. Mogao je dakle ukrasti nešto drugo o čemu ne znamo ništa. Ali, da bi dokazao da nije kriminalac moralo bi se dokazati da nikad nije učinio ništa kriminalno, a to se ne može znati. Dakle, ne može se dokazati da netko nije kriminalac. Tako onaj tko ne tvrdi A nego samo da nije ne-A često insinuira da A. Kad je riječ o realizmu matematike i morala, Clarke-Doane se koristi, kako je uočio Leitner, također nedovršenim zaključivanjem. Ne zagovaram moralni realizam, nego samo da se argumenti protiv njega mogu primijeniti i na matem,atički realizam, i sl.

[xi] Clarke-Doane tu nesvodivost morala na teoriju naziva radikaliziranjem Open Question argumenta, ali nije jasno što se dogodilo s Mooreovim OQA iz prethodne bilješke 9.

[xii] Razlike matematike i fizike, odnosno njihove karakteristike, u tom je duhu- komentirao i Richard Feynman. Ovdje je video https://www.youtube.com/watch?v=IaSN-3JAVTg&ab_channel=MarkStump, a ovdje su najznačajniji uvidi https://www.cantorsparadise.com/richard-feynman-on-the-differences-between-mathematics-and-physics-c0847e8a3d75

[xiii] Ovdje citirano prema Shearmur, Jeremy (2004): Popper Versus Analytical Philosophy? ANU Research Publications https://openresearch-repository.anu.edu.au/handle/1885/87446

[xiv] Shermur (ibid) piše kako je bio začuđen tendencijom analitičkih filozofa da obične ideje iz diskusije predstave u simboličkoj i općoj formi, slično kao što su njihovi srednjovjekovni prethodnici stvari prevodili na hebrejski, ali su oni barem imali izgovor da je hebrejski božji jezik.