Pitagorin zakon malih brojeva. Od glazbe do fizike i natrag

U svojem drugom eseju o matematici glazbe, Zvonimir Šikič objašnjava matematičku logiku tonova i konsonantnosti, započinjući s otkrićem Pitagorejaca, pojašnjavajući fizikalni model zvuka kroz niz primjera koji se mogu čuti i vidjeti, te čini puni krug natrag do glazbe.

• Naslovna fotografija: Akustična gitara (CC0)

• Prethodni članak o matematici glazbe: Dvanaest veličanstvenih. Matematika glazbene oktave

• Problem

Pitagorejci su vjerovali da su principi matematike principi svega. Polazna točka ovog prilično općenitog uvjerenja bila je njihovo otkriće “zakona malih brojeva” tj. njihovo otkriće da je visina tona žice na liri jednostavno povezana s njenom duljinom. Kad se dužina skrati u omjeru 1:2 visina tona skoči za oktavu, kada se skrati u omjeru 2:3 ona skoči za kvintu, u omjeru 3:4 za četvrtinu, u omjeru 4:5 za veliku tercu itd. Ukratko, omjeri malih cijelih brojeva izvor su konsonantnosti – što manji brojevi to veća konsonantnost.

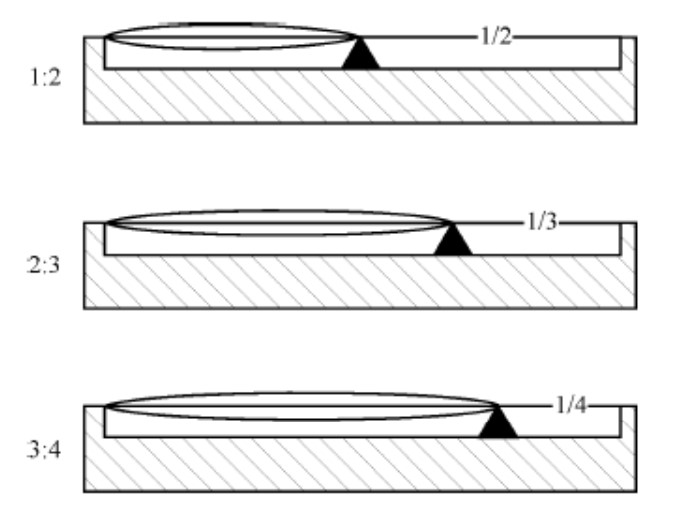
Skratiti duljinu žice znači povećati njenu frekvenciju. Dakle, pitagorejci su otkrili da je omjer frekvencija između oktave i temeljnog tona 2:1, između kvinte i temeljnog tona  3:2, između kvarte i temeljnog tona 4:3 itd.

Ohrabreni ovim uspjehom, pitagorejci su pokušali cijeli univerzum opisati pomoću jednostavnih harmonijskih odnosa. Od harmoničnih ili neharmoničnih rezonancija u ljudskom tijelu (koje je u koruptivnom sublunarnom području) do harmonije sfera (koja je u vječnom i ne koruptivnom supralunarnom području). Koristeći nomenklaturu jednog kasnijeg doba, musica instrumentalis tj. obična glazba, postala je musica humana i musica mundana koje objašnjavaju mnogo više od obične glazbe.

Ono što nas ovdje zanima je sljedeće pitanje. Ima li naše razlikovanje konsonantnih i disonantnih intervala neki temelj u činjenicama “tamo vani” u stvarnom svijetu ili je pak subjektivno?

Čini se da je zakon malih brojeva već dao odgovor na to pitanje. On jasno dokazuje da postoji nešto jedinstveno “tamo vani” što doživljavamo kao konsonantnost “tu unutra”. Ovaj jedinstveni izvor našeg razlikovanje konsonantnih i disonantnih intervala (kao „uhu ugodnih i uhu neugodnih“) harmonijski je niz frekvencija 1f : 2f : 3f : 4f … . Taj početni niz cjelobrojnih frekvencija vanjski je uzrok konsonantnosti i razlikuje se od ne cjelobrojnih nizova koji rezultiraju disonantnošću. U tom su smislu naša razlikovanja konsonantnih i disonantnih intervala objektivna, a ne subjektivna.

Ovo objektivno objašnjenje uobičajeno je mišljenje o toj temi u zapadnoj umjetnosti i znanosti. Možemo ga ilustrirati s citatom jednog od najvećih  znanstvenika 17. stoljeća:

Zakoni glazbe nepromjenjivi su, fiksirani prirodom, stoga bi  trebali vrijedi ne samo za cijelu Zemlju, već i za stanovnike drugih planeta.

1994. Huygens prema (Perlman, 1994.).

Sličan stav ima i jedan od najvećih kompozitora 20. stoljeća:

Glazba – bila ona folk, pop, …, tonska, atonalna, …, prošla, buduća, … – sva ima zajedničko podrijetlo u univerzalnom fenomenu harmonijskog niza. (Bernstein, 1976).

Ali jedan je veliki problem s tim općim mišljenjem. To je postojanje ne zapadnih glazbenih tradicija čiji konsonantni intervali nemaju ništa s harmonijskim nizom. Na primjer, gamelan udaraljkaški orkestri koji spadaju u autohtonu glazbenu tradiciju Jave i Balija, koristite se 5-tonskom slendro i 7 tonskom pelog ljestvicom, a nijedna nije ni blizu zapadnim harmonijskim ljestvicama. Njihovi konsonantni intervali temelje se na nizovima frekvencija koje nisu cjelobrojne.

Izgleda da ipak ne postoji ništa jedinstveno “tamo vani” po čemu ljudi razlikuju konsonantnost od disonantnosti  “tu unutra”. Čini se da su naša razlikovanja ipak subjektivna, a ne objektivna.

Suočeni smo s dva potpuno suprotna zaključka. Prema zakonu malih brojevi Pitagorina intonacija koja se još zove točnom ili prirodnom i koja se temelji na nizu cjelobrojnih frekvencija, ljudska je univerzalija. No, ako uzmemo u obzir postojanje ne zapadnih glazbenih tradicije, čije se ljestvice temelje na mnogo različitih nizova necjelobrojnih frekvencija, ona ipak nije ljudska univerzalija.

• Druga dimenzija problema

Postoji i druga dimenzija problema. Je li naše razlikovanje konsonantnosti i disonantnosti urođeno (kao što smo do sada prešutno pretpostavljali) ili ono ovisi o našim iskustvima? Drugim riječima, jesu li ta razlikovanja urođena ili stečena? (Pod urođenim mislim na proizvod evolucije, a pod stečenim mislim na proizvod kulture.) Prema zakonu malih brojeva čini se da su ona urođena i objektivna. U skladu s činjenicom postojanja različitih glazbenih tradicija ona bi mogla biti stečena i subjektivna ili možda urođena i subjektivna.

Prije nego nastavim dopustite da s nekoliko primjera pokažem da se neka druga auditorna razlikovanje mogu složiti u bilo koju od dostupnih kombinacija. Naše razlikovanje glasnog i tihog je urođeno i objektivno; razlikovanje gudačkog i puhačkog instrumenta stečeno je i objektivno; razlikovanje ružne i lijepe glazbe stečeno je i subjektivno; a razlikovanje materinjeg i stranog jezika je urođeno i subjektivno.

Prevladava mišljenje da je razlikovanje konsonantnosti i disonantnosti stečeno i stoga promjenjivo. Oko ovog mišljenja razvilo se mnogo glazbeno političke gluposti.

Glazbeni rasistički imperijalizam: Glazba drugih kultura trebala bi evoluirati prema zapadnim superiornim formama koje se temelje na nepromjenjivim zakonima prirode.

Glazbeni kulturni imperijalizam: Glazba drugih kultura trebala bi evoluirati prema našim superiornim formama koje proizvodi naša superiorna kultura.

Glazbeni kozmopolitizam: Sve su glazbene tradicije jednako vrijedne i trebale bi utjecati jedna na drugu.

Glazbeni nacionalizam: To je naša glazba i ne želimo nikakve utjecaje.

Utoliko ukoliko se temelji na pojmu konsonantnosti, to je sve pogrešno, jer se temelji na irelevantnim empirijskim podacima. Osim toga ne uzima u obzir što se dogodilo sa zakonom malih brojeva u posljednjih petsto godina, niti uzima u obzir razumijevanje drugih glazbenih tradicije do kojeg smo došli u prošlom stoljeću. Evo i objašnjenja tih „novosti“.

• Galileova teorija

Primijetite da pitagorejci nisu ponudili objašnjenje zakona malih brojeva. Da biste do njega došli, trebate imati bar neke ideje o zvuku.

Ako se usredotočite na perceptivni aspekt, zvuk je osjet koji u organu sluha stimuliraju vibracije zraka s frekvencijama u rasponu od 20 do 20 000 Hz. Vibracije su vibracije tlaka zraka, koje su poznatije pod imenom zvučni val. Njegovo je djelovanje objašnjeno na sljedećoj slici.

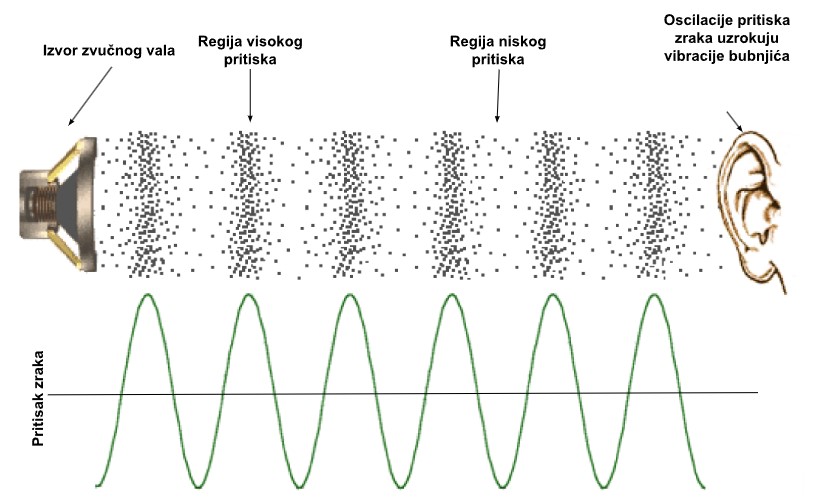
Vrhovi sinusoide odgovaraju zatamnjenim područjima. Ona predstavljaju područja zgušnjavanja molekula zraka. To su područja višega tlaka. Doline sinusoide predstavljaju smanjenu gustoću zraka. To su područja nižega tlaka. Val potiskuje bubnjić u trenucima povišenog tlaka, a izvlači ga u trenucima sniženog tlaka i tako uzrokuje vibracije bubnjića. Te vibracije percipiramo kao zvuk.

U skladu s ovom općom idejom Galileo je ponudio jedan od prvih objašnjenja zakona malih brojeva (Galilei, 1974.)

… ugodne konsonancije su parovi tonova koji pogađaju uho s određenom pravilnošću; ta se pravilnost sastoji u tome da su udari koje isporučuju dva tona, u istom vremenskom intervalu, sumjerljivi u broju, kako ne bi bubnjić dovodili u stalnu muku savijanja u dva različita smjera …

Gustoća Galileovih udara određena je periodima odgovarajućih zvučnih valova. Ako ih prikažemo kao na donjoj slici, onda broj točaka po jedinici intervala predstavlja odgovarajuću frekvenciju.

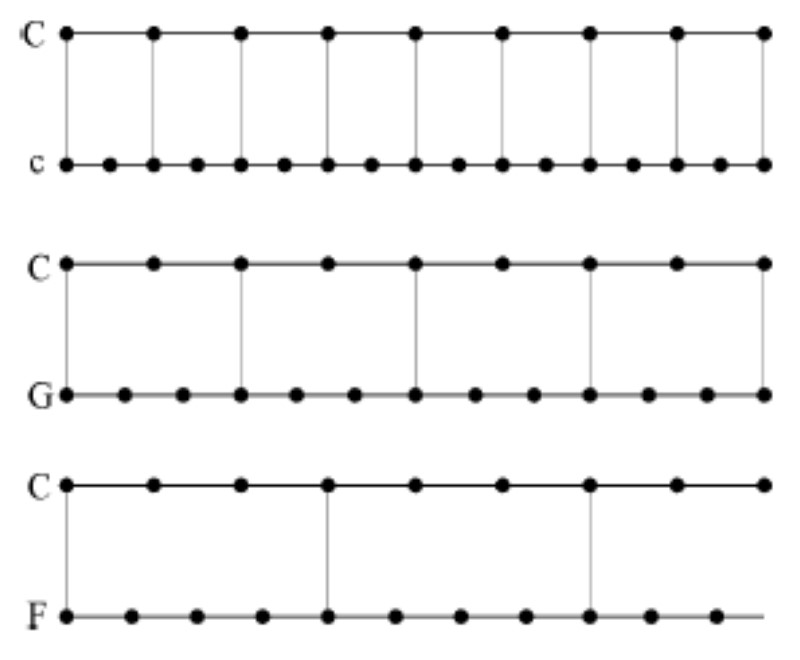
Gledajući ovaj prikaz mogli bismo reći da je jedna polovica oktave c sadržana u temeljnom tonu C i to objašnjava blisku vezu oktave i njenog temeljnog tona. Slično, jedna trećina kvinte G sadržana je u temeljnom tonu C i to objašnjava malo manju bliskost kvinte i njenog temeljnog tona. Na isti je način u temeljnom tonu C sadržana jedna četvrtina kvarte F, jedna petina velike terce, jedna šestina male terce itd. To objašnjava njihove opadajuće konsonantnosti.

Galileova teorija je jako lijepa i često citirana, čak i danas, ali postoji jedan veliki problem s tom teorijom. Ona nije istinita.

• Istinita teorija

U važnom eksperimentu iz 1965. Plomp i Levelt istraživali su kako neuvježbani slušatelji prosuđuju disonantnost 70 raznih intervala kada ih ostvaruju parovi tonova koji su čisti sinusni valovi. Dakle, radi se o tonovima s jednom jedinom frekvencijom bez viših harmonika (v. dolje). Rezultat pokusa je predstavljen krivuljom disonance.

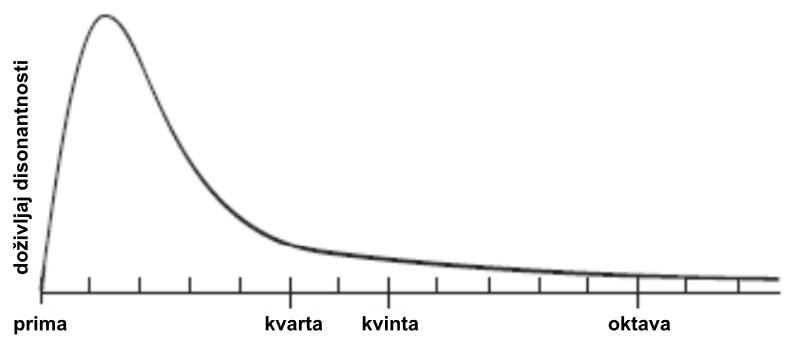
(1) Disonantnost je nula kada oba sinusna vala imaju istu frekvenciju.

(2) Disonantnost brzo raste do svog maksimuma negdje oko sekunde.

(3) Zatim se disonantnost ravnomjerno smanjuje natrag prema nuli.

Primijetite da se za čiste sinusne valove velika septima i mala nona, po doživljenoj disonantnosti, gotovo ne razlikuju od oktave. To je u potpunoj suprotnosti s Galilejevom teorijom.

Helmholtz je objasnio što se ovdje događa, gotovo stoljeće prije nego što su Plomp i Levelet proveli svoj eksperiment (relevantan eksperiment Helmholtzu nije bio dostupan, jer mu nisu bili dostupni čisti sinusni zvučni valovi koje lako generiraju današnja računala). On je svoje objašnjenje temeljio na fenomen udara.

Fenomen udara nastaje alternacijom konstruktivne i destruktivne interferencije zvučnih valova. Kada dva sinusna vala potpuno iste frekvencije slušamo zajedno, oni zvuče kao jedan val. Ali takva kombinacija

može biti glasnija ili tiša od originalnih valova. Kad su valovi u fazi, tj. kada imaju istu početnu točku, njihovi vrhovi i doline točno se poklapaju pa je zbroj veći od pribrojnika. To je konstruktivna interferencija. Kad valovi nisu u fazi, vrhovi jednog vala mogu se poklopiti  s dolinama drugog i tada je zbroj valova manji od pojedinačnih valova. To je destruktivna interferencija.

Što se dešava ako se dva sinusna vala tek malo razlikuju u frekvenciji? Najlakši način da to zamislimo jest da zamislimo da su to dva vala iste frekvenciji, kojima se njihova relativna faza polako mijenja. Kada su faze poravnate one se zbrajaju konstruktivno; kada su pomaknute zbrajaju se destruktivno. Rezultat su udari.

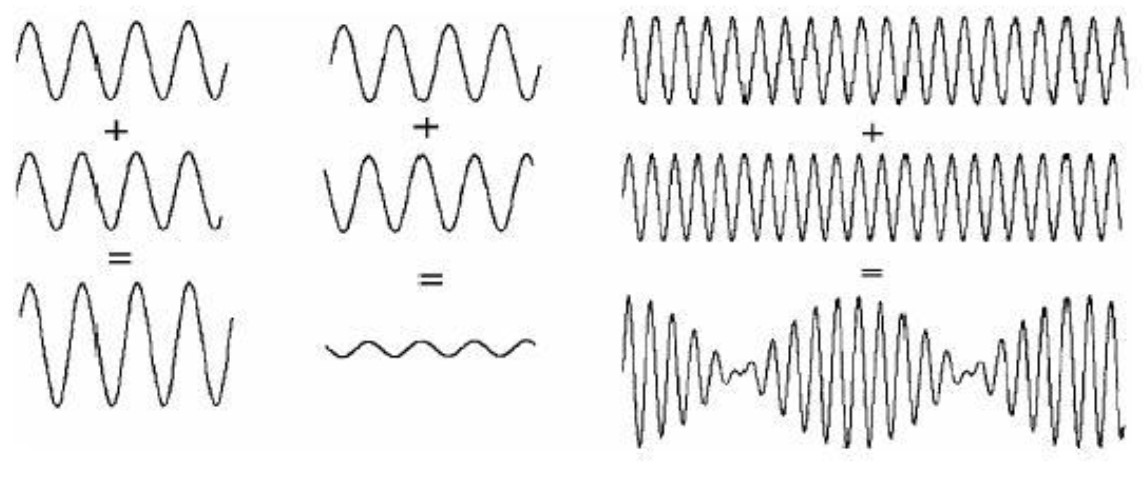
Sada je lako razumjeti već najavljeno Helmholtzovo objašnjenje:

(1) Kada su sinusni valovi vrlo bliskih frekvencija, čuju se kao jednostavan ugodan ton sa sporim vibracijama u glasnoći. Fizičko porijeklo ovog ugodnog vibrata je fenomen udara.

(2) Uz nešto veću razliku u frekvenciji udari postaju brži i to se doživljava kao disonantnost.

(3) Nakon toga tonovi se odvajaju i percipiraju se pojedinačno kao konsonantan par.

To je ilustrirano na sljedećoj slici.

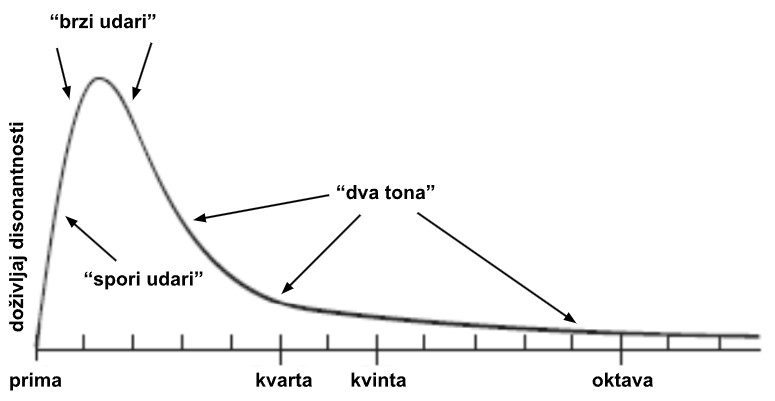
To sve možete i čuti:

Čut ćete čisti sinusni ton od 220Hz 4 sekunde. Zatim ćete čuti čisti sinusni ton od 221Hz 4 sekunde. Razlikuju se za 8 centa (100 centa je pola tona). I na kraju ćete čuti oba tona zajedno 8 sekundi. Jasno se čuju polagani udari.

Čut ćete čisti sinusni ton od 220Hz 4 sekunde. Zatim ćete čuti čisti sinusni ton od 225Hz 4 sekunde. Razlikuju se za cca trećinu tona. I na kraju ćete čuti oba tona zajedno 8 sekundi. Jasno se čuju brzi udari.

Čut ćete čisti sinusni ton od 220Hz 4 sekunde. Zatim ćete čuti čisti sinusni ton od 270Hz 4 sekunde. Razlikuju se za cca dva i pol tona. I na kraju ćete čuti oba tona zajedno 8 sekundi. Jasno se čuju dva tona bez udara.

• Složeni zvukovi

Mi smo zapravo zainteresirani za složene zvučne valove koje proizvode naši glazbeni instrumenti, a ne za čiste sinusne valove koje proizvode računala. Čisti sinusni valovi su važni samo zato što su od njih sastavljeni složeni valovi.

Kao što je složeni svjetlosni val sačinjen od duginog spektra čistih valova pojedinačnih boja, tako se i složeni zvučni val sastoji se od čistih sinusnih valova različitih frekvencija.

Svjetlosni val možemo analizirati pomoću prizme, a zvučni pomoću Fourierove analize.

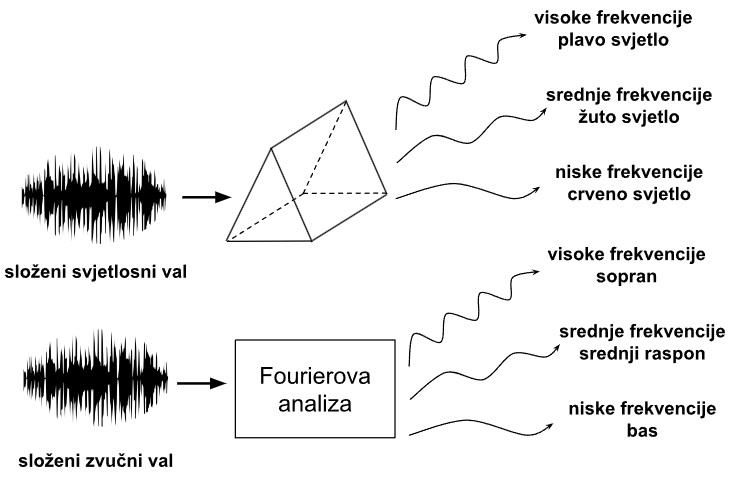
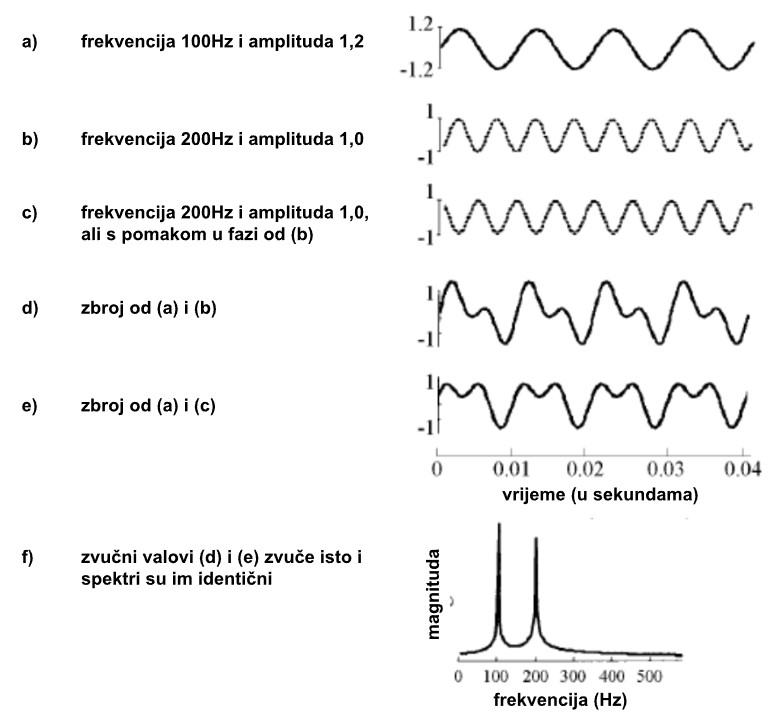
Fourierova analiza svodi složeni zvučni val na njegov spektar frekvencija. Npr. složeni zvučni valovi (d) i (e), koji su (a) + (b) odnosno (a) + (c), oba su reducirana na spektar (f), koji otkriva frekvencije izvornih sinusnih valova.

Naš auditorni sistem je biološki analizator spektra koji radi isto. On pretvara zvučni val u frekvencijski spektar koji ima auditorno značenje. (G. Ohm prvi je predložio ovu ideju 1843.) Ovo je objašnjeno na sljedećoj ilustraciji.

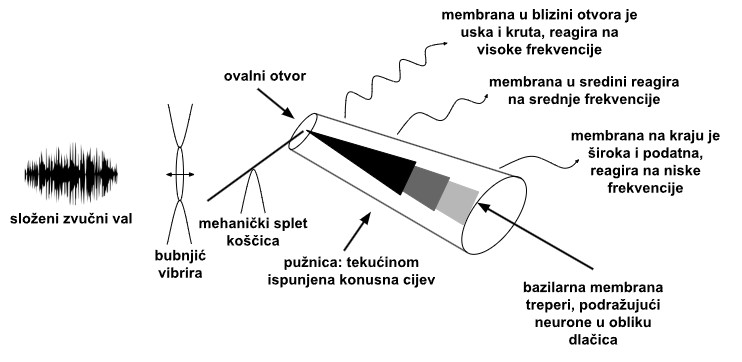
Vibracije se prenose na pužnicu ispunjenu tekućinom, koja je u ilustraciji razvučena. Gibanje tekućine ljulja membranu koja se proteže duž pužnice. Područje najbliža ovalnom otvoru reagira na visoke frekvencije, dok udaljeni kraj reagira na niske frekvencije. Sićušni neuroni koji sjede na membrani šalju poruke prema mozgu kada su zatitrani.

Tako uho prima zvučni val, poput (d) ili (e) na prethodnoj slici, i u mozak šalje reprezentaciju njegovog spektra (f). Ova reprezentacija ima auditorno značenje.

• Harmonijski i neharmonijski zvukovi

Kao što smo već rekli, ono što nas stvarno zanima je kako objasniti disonantnost različitih intervala, koje proizvode složeni zvučni valovi. To su zvukovi koje proizvode naši glazbeni instrumenti.

Prije svega treba reći da postoji velika razlika između složenih zvukova koji su harmonijski i onih koji nisu harmonijski. Predstavljamo ove dvije vrste zvuka s dva primjera.

Tipičan primjer harmonijskog zvuka je zvuk gitare. Evo njegovog spektra.

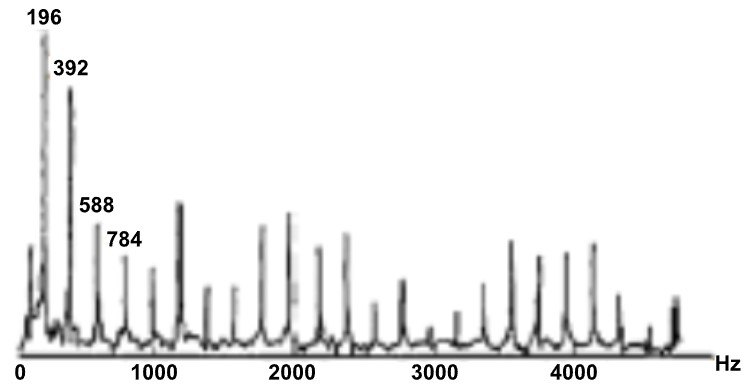
Primijetite da se spektar sastoji od osnovne frekvencije f = 196Hz i od njenih cjelobrojnih višekratnika na 2f = 392Hz, 3f = 588Hz, 4f =784Hz itd. Takav spektar u kojem su sve frekvencije tzv. viših harmonika cijeli višekratnici temeljne frekvencije f naziva se harmonijskim, a odgovarajući zvuk zove se harmonijski zvuk. Budući da se periodi svake viša harmonike ponavljaju točno unutar perioda temeljnoga tona, harmonijski zvučni valovi su periodični.

Tipičan primjer neharmonijskog zvuka je zvuk udarca po metalnoj pločici. Evo njegovog spektra.

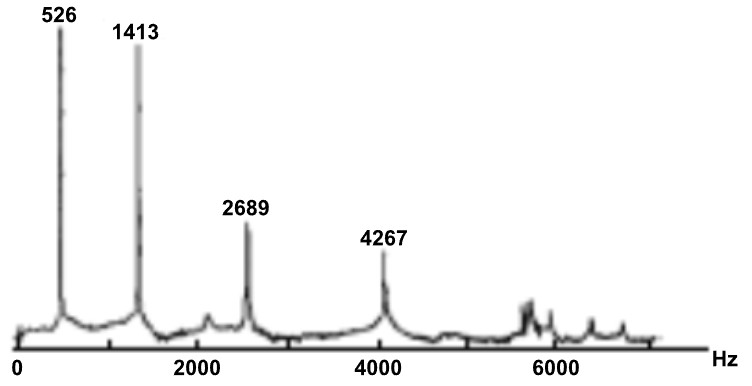
Primijetite da se spektar sastoji od osnovne frekvencije na f = 526Hz i frekvencija viših harmonika koje nisu cjelobrojni višekratnici temeljne frekvencije: 2,68f = 1413Hz, 5,11f = 2689Hz i 8,11f = 4267Hz. Takav spektar u kojem frekvencije nisu cjelobrojni višekratnici temeljne frekvencije f naziva se neharmonijskim i odgovarajući zvuk naziva se neharmonijskim zvukom. Budući da se periodi viših harmonike ne ponavljaju točno unutar perioda temeljnoga tona, neharmonijski zvučni valovi nisu periodični.

Žica i metalna pločica samo su dva od mnogih mogućih izvora zvuka. Gudački instrumenti, kao i mnogi drugi, također su harmonijski. Kada zrak oscilira u puhačkom instrumentu, njegovo je gibanje ograničeno na isti način kao što je gibanje žica ograničena njenim fiksnim krajevima pa su zato i zvukovi puhača harmonijski. Naime, na zatvorenom kraju puhačkog instrumenta tlak zraka mora biti jednak nuli kao i na otvorenom kraju. Nasuprot tome, većina udaraljki kao što su bubnjevi, marimbe, gongovi itd. imaju neharmonijske spektre.

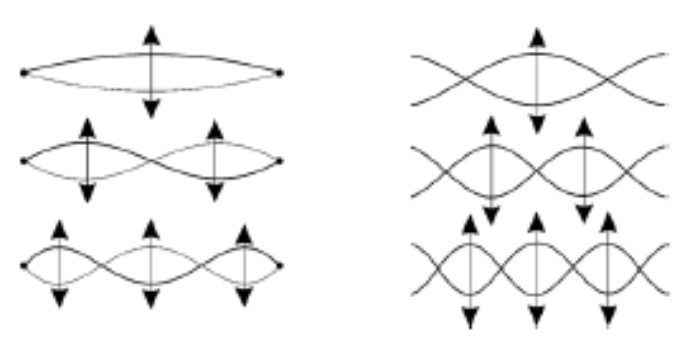
Spektar žice je harmonijski jer je ona fiksirana na oba kraja i može podržati samo one oscilacije koje se točno uklapaju u duljinu žice. Matematički se može dokazati da žica koja vibrira s temeljnom frekvencijom f može imati više harmonike samo s frekvencijama 2f, 3f itd. To je vidljivo na donjoj slici lijevo. Spektar metalne pločice je neharmonijski jer je šipka slobodna na oba kraja. I to se može matematički dokazati, a vidljivo je na donjoj slici desno.

• Teorija za složene zvukove

Vratimo se našem glavnom pitanju. Kako objasniti disonantnost odnosno konsonantnost intervala koje ostvaruju složeni zvučni valovi?

Plomp-Leveltov eksperiment prikupio je podatke samo o percepcijama čistih sinusnih valova. Stoljeće prije toga, kako bi objasnio doživljaj disonantnosti dvaju složenih tonova, Helmholtz je predložio sljedeći postupak:

Zbrojite sve disonantnosti koje generiraju svi parova viših (čistih sinusnih) harmonika dvaju složenih tonova koje testiramo.

Primijetite da čak i ako ne postoji udari uslijed interferencije temeljnih tonova, mogu postojati udari uslijed interferencije njihovih viših harmonika. Evo jednog primjera:

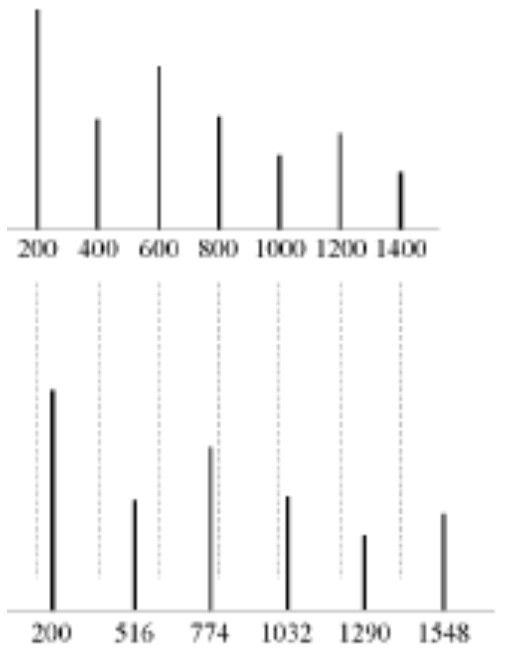
Harmonijski zvuk s temeljnom frekvencijom f = 200Hz slušamo zajedno s harmonijskim zvukom kojem je temeljna frekvencija g = 258Hz. Iako su temeljne frekvencije dovoljno daleko da ne stvaraju udare, neke od viših harmonika su dovoljno blizu da ih stvaraju. To dovodi do određene razine disonantnosti koju računamo tako da zbrojimo sve disonantnosti koje generiraju svi parova viših harmonika.

Krivulja disonantnosti koju nalazimo na taj način prikazana je na sljedećoj slici.

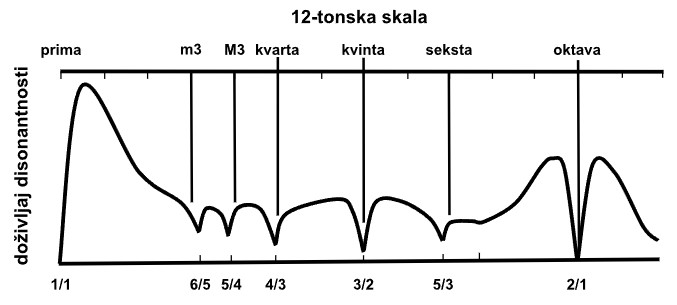
Uočite da se minimumi krivulje disonantnosti podudaraju s intervalima koje opisuje Pitagorin zakon malih brojeva. Matematički se može dokazati da krivulje disonantnosti harmonijskih spektara uvijek imaju ovo svojstvo i to je konačno objašnjenje Pitagorinog zakona malih brojeva za harmonijske zvukove.

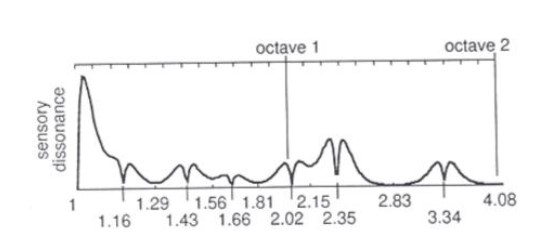
Krivulja disonantnosti za neharmonijski spektar metalne pločice s temeljnom frekvencijom vibracije f, čije više harmonike imaju frekvencije 2.76f, 5.41f, 8.94f, 13.35f i 18.65f prikazana je na sljedećoj slici.

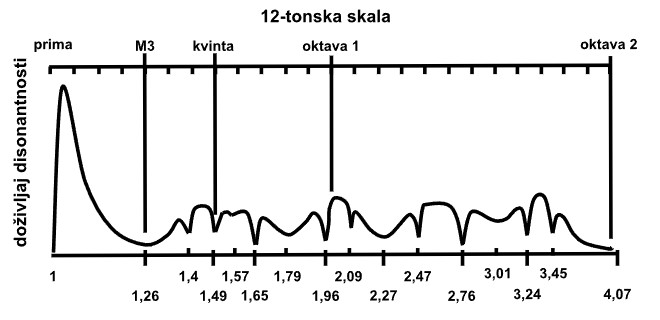
Primijetite da se minimumi krivulje disonantnosti ne podudaraju ni s jednim od Pitagorinih intervale, koje karakterizira zakon malih brojeva (ali se za spektar udaraljki s Jave i Balija poklapa s konsonantnim intervalima slendro i pelog skala). Matematički se može dokazati da krivulje disonantnosti neharmonijskih spektara uvijek imaju ovo svojstvo i to je konačno pobijanje Pitagorinog zakona malih brojeva za neharmonijske zvukove.

• Zaključak

Možemo zaključiti da je zakon malih brojeva samo jedan epifenomen koji je empirijski irelevantan za naša objašnjenja, kao što su to i ne-cjelobrojni “zakoni” slendra, peloga i drugih neharmonijskih skala. Pravi izvor naših razlikovanja konsonantnosti i disonantnosti je fenomen udara, kako je pretpostavio Helmholtz, a izravno su potvrdili Plomp i Level svojim eksperimentom. Udari su stvarno nešto jedinstveno “tamo vani“ što doživljavamo kao disonantnost “tu unutra”. U tom smislu naša su razlikovanja objektivna, a ne subjektivna.

Nadalje, uobičajeno je svim glazbenim tradicijama (harmonijskim ili ne) da razlikuju konsonantne i disonantne intervale na ovaj način. Čini se da je to zajedničko svim ljudima, što znači da su naša razlikovanja konsonantnosti i disonantnosti urođene, a ne stečena i to potvrđuju zapadne harmonijske tradicije kao i ne zapadne neharmonijske tradicije.

Da budemo precizniji, možemo reći da je doživljaj konsonantnosti i disonantnosti funkcija intervala i spektra zvuka. Muzička skala i spektar su povezani ako krivulja disonantnosti za taj spektar ima minimume u intervalima te skale. Harmonijski spektri zapadnih glazbenih instrumenata su povezani sa zapadnim ljestvicama koje sadrže Pitagorine intervale. Neharmonijski spektri drugih glazbenih tradicije povezani su s njihovim skalama.

I to možete čuti:

Čut ćete skladbu koja koristi harmonijski zvuk i skalu povezanu s tim zvukom (tj. minimumi krivulje disonantnosti toga zvuka su dio te skale). Naravno, to zvuči dobro.

Sada ćete čuti istu skladbu koja koristi harmonijski zvuk i skalu koja je „rastegnuta“ tako da je oktava 2.1 a ne 2 (i analogno su „rastegnuti“ svi ostali intervali). Ta skala, naravno, nije povezan s tim zvukom (tj. minimumi krivulje disonantnosti toga zvuka nisu dio te skale) i to ne zvuči dobro.

Sada ćete čuti istu skladbu koja koristi „rastegnutu“ skalu i  neharmonijski zvuk koji je usklađen s tom skalom (tj. minimumi krivulje disonantnosti toga zvuka dio su te skale). Ta  „rastegnuta“ skala je povezana s tim neharmonijskim zvukom i to zvuči dobro (iako malo neobično).

Na kraju ćete čuti istu skladbu koja koristi neharmonijski zvuk (usklađen s „rastegnutom“ skalom) i standardnu nerastegnutu skalu. Ta skala, naravno, nije povezana s tim zvukom (tj. minimumi krivulje disonantnosti toga zvuka nisu dio te skale) i to ne zvuči dobro.

I ovo nije cijela priča. neki suvremeni glazbenici skladaju za vrlo neobične zvukove. U skladu s prethodnim objašnjenjima, njihov postupak je sljedeći:

(1) Odaberu zvuk.

(2) Pronađu spektar tog zvuka.

(3) Pojednostave taj spektar.

(4) Izračunaju njegovu krivulju disonantnosti.

(5) Konstruiraju odgovarajuću skalu koja sadrži minimume te krivulje.

(6) Sintetiziraju instrumente koji proizvode tonove te skale.

(7) Skladaju u toj skali i sviraju na tim instrumentima.

Takva je skladba W. Setharesa „Chacko canyon rock“.

(1) Odabrani zvuk je zvuk drobljenja kamena pod gojzericom u kanjonu iz naslova.

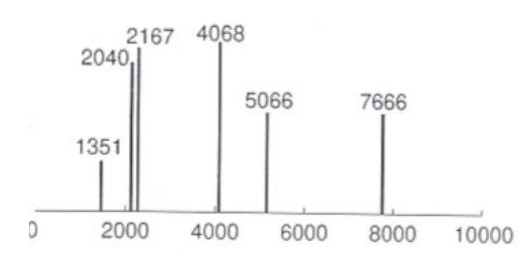
(2) Spektar tog zvuka izgleda ovako:

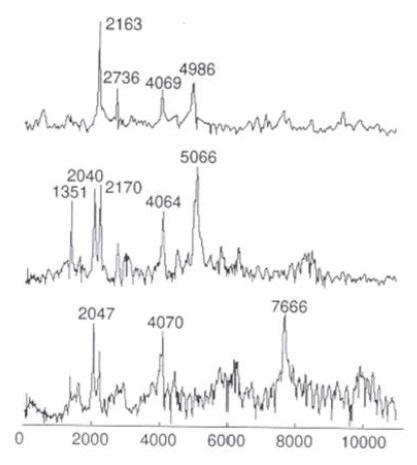
(3) Pojednostavljeni spektar izgleda ovako:

(4) Njegova krivulja disonantnosti izgleda ovako:

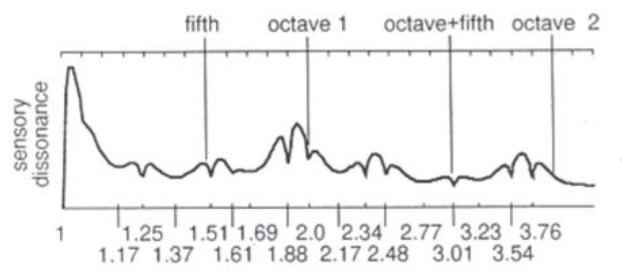
(5) Odgovarajuća skala je:

(6)&(7) Nakon sintetiziranja odgovarajućih instrumenata Seathers je skladao sljedeću kompoziciju:

Još jedna Seathersova skladba za zvuk malih zvona je „Tingshaw “. Postupak je bio sljedeći.

(2)

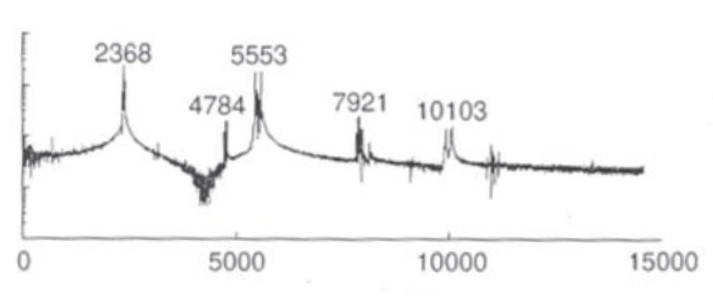
(3)

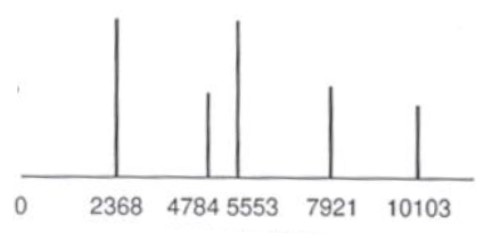
(4)

(5)

Skladba za zvuk malih zvona zvuči ovako:

Napravili smo puni krug. Od glazbe, do prvih empirijskih zakona, do njihovog matematička razumijevanja i fizičkih potvrda, i konačno natrag do glazbe.

• Izvori

Bernstein, L., 1976, The Unanswered Question, Harvard University Press.

Galilei, G., 1974, Two New Sciences, transl. by S. Drake, University of Wisconsin Press.

Perlman, M., 1994, American gamelan in the garden of eden: intonation in a cross cultural encounter, Musical Quaterly 78: 510-555.

Sethares, W. A., 1997, Tuning, Timbre, Spectrum, Scale, Springer.

Šikić, Z., Mathematics, physics and music – A case study, Role of Mathematics in Physical Sciences: Interdisciplinary and Philosophical Aspects, eds. G. Boniolo, P. Budinich, M. Trobok, 179–196, Springer Science 2005