Pravu američko-rusku utrku odavno nismo imali… Cilj je na vidiku, ali tko je bliže

U drugom članku o kvantnim računalima govori se o njihovoj konkretnoj primjeni, prikazuje se kolika ubrzanja nude i kakve bi posljedice komercijalno dostupna kvantna računala imala na sigurnost na Internetu i kriptovalute, dizajn novih lijekova i materijala, te modeliranje klime, prometa ili ekonomije. Američke velike tvrtke i Ruski kvantni centar grade podjednako velika računala

• Naslovna slika: Na korporativnoj stranici proizvođača kvantnih računala D-Wave Systems ovo je ilustracija za nagradu za AI optimizaciju planiranja koja je izvedena na njihovom računalu

U prvom članku o kvantnim računalima upoznali smo qubite i njihova svojstva koji ih fundamentalno razlikuju od bitova: superpoziciju stanja i kvantnu spregnutost. Lukavim iskorištavanjem mogućnosti koje nam pružaju qubiti, kvantna računala postižu ogromna ubrzanja u odnosu na klasična prilikom rješavanja nekih problema.

U ovom članku bavit ćemo se pitanjima konkretne primjene kvantnih računala, te pokušati prikazati kolika su ubrzanja koja kvantna računala nude. Vidjet ćemo kakve bi posljedice komercijalno dostupna kvantna računala imala na sigurnost na Internetu i kriptovalute, dizajn novih lijekova i materijala, te modeliranje klime, prometa ili ekonomije.

Osim toga, objasnit ćemo i zašto su toliko skupa i kakva je perspektiva njihova razvoja.

„Teški“ i „laki“ problemi

Da bismo mogli odgovoriti na pitanja vezana uz ubrzanje koje kvantna računala nude, prvo je potrebno reći nešto o tome koje probleme moderna računalna znanost smatra „lakima“, a koje „teškima“.[i]

„Laki“ problemi su oni za koje vrijeme potrebno za rješavanje ne raste jako brzo s veličinom problema (koju ćemo označavati s n).[ii] To su sortiranje brojeva, zbrajanje, množenje i druge osnovne matematičke operacije, zatim traženje zajedničkog nazivnika ili računanje prirodnih konstanti (na primjer pi ili e) s točnošću od n decimala. Zajedničko većini tih problema jest da se na neki način mogu razdvojiti na manje probleme, čije rješavanje pomaže u rješavanju ukupnog problema. Primjerice, quicksort algoritam (na slici) dijeli skup brojeva koji treba sortirati na manje skupove, koje onda individualno sortira. Također, računanje prirodnih konstanti može se razviti u red čije se članove može neovisno izračunati. „Laki“ problemi nisu problem modernim računalima, i mogu se riješiti za izuzetno velike vrijednosti n.[iii]

Quicksort algoritam dijeli skup brojeva na manje skupove, koje onda individualno sortira

Računanje prirodnih konstanti može se razviti u beskonačni red čije se članove može neovisno izračunati, a konačna točnost ovisi o broju članova koje smo izračunali.

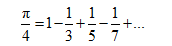
Što su onda „teški“ problemi? Zamislite da organizirate svadbu, a svaki od gostiju ima popis ljudi (oko pola uzvanika) s kojima nikako ne želi sjediti za stolom. Očito, organizacija postaje noćna mora, a pronalazak rješenja vrlo težak u slučaju velikog broja gostiju. Da stvar bude još gora, za svakog novog gosta može se dogoditi da ga je nemoguće smjestiti u postojeći raspored, pa treba krenuti ispočetka. Sličan je i problem putujućeg trgovca (travelling salesman problem), u kojemu treba pronaći način kako obići svaki od n gradova, a da se pritom potroši minimalna količina goriva.

Pronalazak optimalnog načina kako posjesti poznanike, prijatelje i parove u kinu također je „težak“ problem. Preuzeto s https://xkcd.com/173/

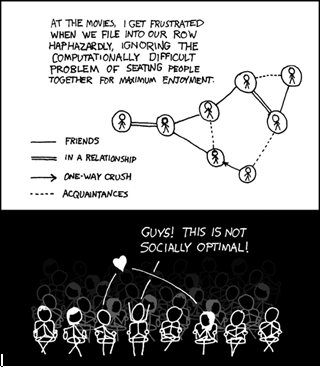
Zašto su ti problemi tako teški? Zato što je svaki novi član (grad ili gost) u nekakvom odnosu (interakciji) sa svim ostalim članovima, što znači da se broj tih odnosa vrtoglavo povećava povećanjem veličine problema (n). U pravilu, moguće je pronaći nekakvu prečicu, no za dovoljno velike n „teški“ su problemi klasičnim računalima praktički nerješivi.

U stvarnom svijetu „teški“ se problemi često javljaju kada nešto želimo predvidjeti ili optimizirati. Vremenska prognoza za Hrvatsku bit će točnija ako uključimo i podatke i predviđanja za susjedne zemlje, koje opet ovise o vremenskim prilikama u njima susjednim zemljama, i tako dalje. Slično je i u ekonomiji – predviđanje cijene dionica neke firme uključuje praćenje velikog broja međusobno povezanih varijabli (pa i vrijednosti dionica drugih firmi), a „teški“ problemi javljaju se i prilikom optimizacije na primjer tijeka gradskog prometa, gdje svako raskršće utječe barem na sva susjedna.

Koliko ubrzanje?

I ovdje u priču ulaze kvantna računala. Kao i u „teškim“ problemima, svi qubiti u kvantnim računalima – bili to ohlađeni ioni ili supravodljivi sklopovi[iv] – su međusobno povezani (kvantno spregnuti) sa svima ostalima. Upravo zbog te arhitekturalne sličnosti, kvantna računala su posebno korisna za rješavanje „teških“ problema.

Kada govorimo o rješavanju konkretnih problema optimizacije, nije moguće zaobići kanadsku firmu D‑Wave Systems. Ta se kompanija specijalizirala za proizvodnju kvantnih računala namijenjenih rješavanju gore navedenih „teških“ problema, obećavajući (kvadratno) ubrzanje u odnosu na klasična računala.[v] Iako uspjeh računala D-Wavea u tim zadacima (još) nije potvrđen, njihovi dosadašnji kupci su Lockheed Martin i NASA (dizajn letjelica), Google (pretraživanje i strojno učenje) i Temporal Defense Systems, firma koja se bavi internetskom sigurnošću. Kvantno računalo kupio je i Britanski meteorološki ured (UK Met Office), a za cijelu priču zainteresirana je i velika švicarska banka UBS. Međutim, za razliku od IBM-ovog računala opisanog u prošlom članku, računala D-Wavea nisu univerzalna, već mogu ubrzati rješavanje samo određenih problema.

A kolika su ta ubrzanja? Kao i klasična računala, ona kvantna korisna su koliko i algoritmi koji se na njima vrte. Ako nemamo dobar algoritam (odnosno koreografiju interferencije, detaljnije opisanu u prethodnom članku) za rješavanje nekog problema, ne možemo postići ubrzanje. Za većinu gore nabrojanih problema optimizacije kvantna bi računala mogla pronaći prečice koje bi dovele do značajnog ubrzanja, ali ih i dalje ostavila u klasi „teških“ problema.

Za većinu nabrojanih problema optimizacije kvantna bi računala mogla pronaći prečice koje bi dovele do značajnog ubrzanja, ali ih i dalje ostavila u klasi „teških“ problema.

Dakle, besmisleno je govoriti da su kvantna računala tisuću, ili milijun milijardi puta brža od klasičnih – ubrzanje ovisi o efikasnosti algoritma (u gornjem primjeru, prečica smanjuje broj koraka potreban za rješenje za faktor 2) i veličini problema. Što je problem (n) veći, od kvantnog računala imamo više koristi.

Računalna alkemija – transmutacija teških problema u lake

	Vrijeme rješavanja
	n = 16	n = 32	n = 64
Težak problem	66 sekundi	50 dana	584 milijuna godina
Težak problem (prečica)	<1 sekunde	66 sekundi	50 dana
Lak problem	<1 sekunde	1 sekunda	4 sekunde

Ipak, najveću korist možemo dobiti u slučajevima kada postoje algoritmi koji pretvaraju „teške“ probleme u „lake“. U takvim slučajevima, kvantna računala zbilja nude potencijalnu revoluciju u smislu da omogućuju značajno povećanje n, odnosno pretvaraju praktički nerješive probleme u dječju igru (na primjer, u igrama djeca zbrajaju bodove – što je „lak“ problem).

Za sad, postoje dva vrlo značajna problema za koje su pronađeni, testirani i potvrđeni algoritmi koji daju tako dramatična ubrzanja (rješavaju probleme u polinomijalnom umjesto u eksponencijalnom vremenu, odnosno pretvaraju „teške“ probleme u „lake“).[vi] To su modeliranje kvantno‑mehaničkih sustava i faktorizacija brojeva Shorovim algoritmom.

Modeliranje kvantnog svijeta kvantnim alatom

„Priroda nije klasična… Želimo li simulirati Prirodu, to treba napraviti kvantno‑mehanički, i nije li to krasan problem, jer baš i ne izgleda jednostavno.“

Richard Feynman, 1981.[vii]

Već u osamdesetim godinama prošlog stoljeća pojavila se ideja kako su klasična računala beznadno neupotrebljiva za simuliranje ponašanja fotona, elektrona i drugih kvantno-mehaničkih čestica. Otad, računala su napredovala nevjerojatno brzo i postala nevjerojatno snažna i jeftina, pa je modeliranje proteina ili ugljičnih vlakana postalo stvarnost (o čemu smo već pisali). Međutim, simulacija kvantnih sustava i dalje je vrlo „težak“ problem, jer dodatak svake nove čestice može potpuno izmijeniti cijelu priču (atomi natrija s 10 elektrona nalaze se u soli i našim stanicama, dok oni s 11 elektrona eksplozivno reagiraju u dodiru s vodom). U molekulama, svi su elektroni u interakciji sa svima ostalima, slično kao i gosti na vjenčanju.

Kako kvantna računala mogu pomoći? Stvar je u tome da i qubiti pokazuju ista kvantna svojstva – kvantnu spregnutost i superpoziciju stanja – kao i fotoni ili elektroni u molekulama! Prema tome, kvantnim računalima, koja su sama kvantni sustavi, prirodno je i „lako“ opisivati druge kvantne sustave – jedino je potrebno imati qubita koliko i čestica koje simuliramo.

Dakle, kada kvantna računala dovoljno „narastu“ moći ćemo simulirati proteine, stanične membrane i DNA te njihovu interakciju s djelatnim molekulama (lijekovima ili patogenima) ne samo s puno većom točnošću nego sada, nego i daleko brže! U takvim sustavima, veličina problema (n) odgovara broju elektrona koji je u tisućama, što znači da su potencijalna ubrzanja reda veličine gugola (10¹⁰⁰).

Takva ubrzanja bit će korisna za razumijevanje mehanizma mnogih bolesti – Alzheimerova, Huntingtonova i Parkinsonova bolest povezane su s pojavom proteina pogrešnog oblika (konformacije), a analiza DNA osobito je važna u borbi protiv karcinoma i genetskih bolesti.

Osim u kemiji i molekularnoj biologiji, potrebu za simulacijom kvantnih sustava imamo i u fizici, pa bi tako kvantna računala mogla dramatično olakšati potragu za novim materijalima – efikasnim solarnim ćelijama (fotoelektrički efekt opisuje interakciju fotona i elektrona) i novim supravodičima.

Magičnih 50 qubita

Na kraju, preostaje nam odgovoriti pitanje – kada će konačno kvantna računala imati dovoljno qubita da mogu konkurirati klasičnima? Trenutno, IBM nudi mogućnost rada na računalu od 20 qubita. Kad bi se kvantna računala ponašala kao klasična, mogli bismo spojiti pet takvih i dobiti jedno od 100 qubita, što bi vjerojatno bilo među najmoćnijim računalima na svijetu. Nažalost, takvo spajanje baš i nije jednostavno.

Sjetimo li se prethodnog članka, u kvantnom računalu mi manipuliramo superpozicijom stanja (svih) qubita sve do trenutka kad ne izvršimo mjerenje i zabilježimo rezultat. To znači da su svi qubiti u interakciji sa svima ostalima (kao i gosti na onom „teškom“ vjenčanju – logično, zar ne?). Da stvar bude još kompliciranija, stanje jednog qubita (pa tako i cijelog računala) može se promijeniti vrlo lako – većina kvantnih računala može održati koherenciju (stanje bez vanjskih utjecaja) svega par milisekundi, što znači da se kod (cijeli jedan korak algoritma) mora izvršiti u tom vremenu.

Ipak, Google je u lipnju hrabro najavio da će do kraja 2017. predstaviti računalo s 50 qubita. No, podjednako velika računala grade i Ruski kvantni centar (RQC) i IBM, pa čak i neki fakulteti i privatne tvrtke. U čemu je stvar? 50 qubita smatra se granicom kvantne nadmoći (quantum supremacy), odnosno brojem za koji kvantna računala dostižu brzinu modernih klasičnih računala. A pravu rusko‑američku utrku nismo imali dugo…

Faktorizacija brojeva i internetska sigurnost

Postoji li opasnost da kvantna računala probiju (svaku) kriptografsku zaštitu

Autor: Davor Grubiša

Kao što smo već spomenuli, dovoljno veliki “teški” problemi su klasičnim računalima praktički nerješivi. Takvi problemi često su temelj kriptografskih algoritama koji se koriste u svim sferama današnjeg računarstva, što za sigurnu razmjenu podataka na internetu, a što za dugotrajno čuvanje tajnih podataka.

Kod računalne kriptografije razlikujemo dvije vrste algoritama – simetrične, u kojima se isti ključ koristi za kriptiranje i dekriptiranje podataka, te asimetrične kod kojih se jedan ključ koristi za kriptiranje a drugi za dekriptiranje.

Simetrični i asimetrični algoritmi imaju različitu primjenu. Simetričnim algoritmima, poput AES se kriptiraju podaci, bilo da je riječ o podacima koji se šalju standardnim https protokolom, ili podacima koji se spremaju na disk u računalu. Ali, kako bismo na siguran način razmijenili simetrični ključ kojim se kriptiraju podaci, koriste se asimetrični algoritmi poput DSA, Diffie-Hellman i trenutno najpopularnijeg, RSA.

Kombinacijom ovih dviju metoda je moguće na praktičan način napraviti privremeni AES ključ i razmijeniti ga koristeći javnu komponentu RSA algoritma svaki put kada otvorimo neku web stranicu https protokolom ili pošaljemo neki email.

Kod simetričnih algoritama poput AES-a, kvantno računarstvo ne donosi neke posebne promjene jer je ključ tajan i dovoljno dugačak (256 bitova) da je praktički nemoguće dekriptirati bez njega. Međutim, kod asimetričnih algoritama kvantno računarstvo predstavlja veliku promjenu jer je pomoću Shorovog algoritma moguće mnogo brže faktorizirati velike brojeve nego binarnim računalima. Trenutno najrasprostranjeniji kriptografski algoritam – RSA se temelji na pretpostavci nepraktičnosti faktorizacije brojeva pomoću binarnih računala.

Konkretno, da bi se “razbilo” 768-bitni RSA ključ (232 decimalne znamenke) binarnim superračunalima i ponajboljim kriptografima na planeti je bilo potrebno 4 godine uz primjenu svih prečaca kojih su se mogli dosjetiti. Kvantnom bi računalu primjenom Shorovog algoritma za isti posao trebalo oko 1500 qubita (i vrlo malo vremena, jer se „težak“ problem pretvara u „lak“).

No, razloga za paniku koja je nastala ove godine baš i nema jer postoji nekoliko praktičnih problema koji RSA i dalje čine vrlo praktičnim i sigurnim.

Već danas su u praktičnoj primjeni gotovo isključivo RSA ključevi minimalne duljine 1024 bita, a novi ključevi koji se generiraju su uglavnom duljine između 2048 i 4096 bitova. Razlog korištenja ključeva ove duljine je isključivo brzina njihove izrade od samo nekoliko sekundi. Za generiranje RSA ključa duljine čak 16 384 bita prosječnom laptopu potrebno oko jedne minute, a jednom kad je takav ključ generiran, moguće ga je koristiti kao bilo koji drugi. Štoviše, sasvim je realno očekivati da će kroz koju godinu RSA ključevi duljine od nekoliko desetaka kilobita biti najnormalnija stvar.

S druge strane, najnaprednije današnje kvantno računalo je Shorovim algoritmom uspjelo faktorizirati decimalni broj 15 koji je u RSA terminima duljine samo 8 bitova. Sveučilištu u Innsbrucku u suradnji s MIT-em i IBM-om je za to trebalo 4 stabilna korisna qubita i peti za mjerenje rezultata.

Kako bismo ovom metodom i tehnologijom razbili 2048-bitni ključ, bilo bi potrebno oko 4 tisuće logičkih qubita i još nepoznat broj qubita više za mjerenje, ispravak grešaka i ostale pomoćne funkcije koje na toj skali lako mogu biti višestruko veće od samog broja korisnih logičnih qubita. Dakle, govorimo o desecima tisuća qubita koje je potrebno ispravno koordinirati.

Dovođenje kvantnih računala na ovu skalu će vjerojatno trajati desetljećima.

Čak i kada bi netko danas snimao beskrajne količine internet prometa i čuvao ovako kriptiran promet, trebat će pričekati nekoliko desetljeća da bi mogao doći do AES ključa kojim su kriptirani podaci koje je potrebno skladištiti.

Ovo je i glavna pretpostavka svih kriptografskih metoda u računarstvu – isplativost probijanja. Trošak razbijanja u budućnosti mora biti viši od vrijednosti tajnih podataka koji se prenose.

[i] U računalnoj znanosti, problemi se dijele u klase – „laki“ pripadaju u P klasu, a „teški“ u NP. Jesu li te dvije klase zapravo jedna (je li P=NP) veliko je neriješeno pitanje.

[ii] U ovom kontekstu, „jako brzo“ znači ekponencijalno. Dakle, problemi u kojima vrijeme rješavanja s povećanjem veličine problema (n) raste sporije od ekponencijalnog u pravilu se smatraju „lakima“.

[iii] Primjerice, svako moderno računalo, pa čak i mobiteli mogu u sekundi izračunati nekoliko tisuća znamenki p.

[iv] Detaljna usporedba tih dviju izvedbi qubita nalazi se na http://www.pnas.org/content/114/13/3305.full.pdf

[v] Primjer kvadratnog ubrzanja (Groverov algoritam) nalazi se u prethodnom članku

[vi] Klasa problema koji su klasičnom računalu teški, a kvantnom laki zove se BQP (bounded-error quantum polynomial time), a ima i svoju stranicu na wikipediji: https://en.wikipedia.org/wiki/BQP

[vii] Nature isn’t classical . . . and if you want to make a simulation of Nature, you’d better make it quantum mechanical, and by golly it’s a wonderful problem, because it doesn’t look so easy.