Rimska i arapska notacija brojeva (5). Od računanja prstima do postupka na papiru. Materijalna sredstva i razvoj matematike.

U prvom dijelu članka Željko Ivanković prepričava dosadašnju raspravu o zamjeni rimskih brojeva/brojki arapskima, a zatim raspravu proširuje teorijom kognitivne arheologinje Karenleigh Overmann koja posebnu pažnju u formiranju koncepta broja posvećuje materijalnim sredstvima među kojima je i notacija. Ivanković ističe da razvoj nije bio skokovit, od otkrića do otkrića nego postupan i dugotrajan te postavlja pitanje koja je komponenta pozicijske notacije bila presudna za kasnija matematička otkrića

Naslovna fotografija: Rimski džepni abak od bjelokosti. (Inria / J.-M. Rames)

I

Nakon prikaza knjige Reconings lingvističkog antropologa Stephena Chrisomalisa, objavljenog pod naslovom Zašto je arapskim brojevima trebalo više od pola milenija da zamijene rimske, reagirali su dva matematičara, Zvonimir Šikić i Aleksandar Hatzivelkos. U prvoj reakciji (Ključni problem rimskih brojeva. Razvoj prirodnih logaritama) Šikić ističe da „rimski sustav brojki nema nikakav sistematski način prikaza razlomaka i to ga definitivno čini lošim sustavom notacije brojeva” te da “rimske brojke nikada ne bi dovele do logaritama”. Već je u Antici, piše Šikić, “zbog efikasnosti korišten pozicijski sustav. Ne-pozicijski sustavi poput rimskog ili grčkog alfabetskog sustava odbačeni su, kada je trebalo efikasno računati”. Iako implicite, Šikić očito ustraje na tezi da je arapski (pozicijski) sustav notacije brojeva zamijenio rimski jer je efikasniji, upravo na onoj tezi koju Chrisomalis ne prihvaća bez ostatka: Ako je, pita on, indo-arapski sustav izrazito efikasniji zašto je zamjena trajala više od pola milenija?

Chrisomalisovo objašnjenje dugotrajne zamjene rimskih brojeva, prepričano u inicijalnom članku serije, detaljno je raščlanjeno u dvama središnjim poglavljima njegove knjige. Počiva na dva uporišta, na koja Šikić prvenstveno reagira. Prema prvom, notacija brojeva puno prije i više služi prikazu veličina nego računanju. U tisuće godina rimske notacije računalo se raznim varijantama abaka (računaljke). Drugo je Chrisomalisovo uporište relativizacija u čemu su točno arapske brojke efikasnije nego rimske. Na tek jednom mjestu u knjizi spominje da su indo-arapske brojke, koje naziva zapadnima, zaista bile prikladnije ‘visokoj’ matematici, ali ne vidi da je to razlog, ni objašnjenje, dugotrajnosti zamjene notacije. U mnogočemu drugom, recimo u prepoznatljivosti broja, čak i u kratkoći barem nekih zapisa, rimske su efikasnije. Na primjer, rimskom se notacijom tisuću piše kao M, a zapadnom s četiri cifre – 1000.

Hatzivelkos se, u svojoj reakciji na Šikićev članak (Jednostavnost je prednost rimskih brojeva. Egipatsko množenje i intuitivno zbrajanje), složio da je rimska notacija brojeva zaista „ograničavajući faktor za razvoj matematike“, ali opća populacija, piše Hatzivelkos, „nije koristila algoritme, kao ni precizne astronomske izračune“. Svakodnevne je matematičke operacije općoj populaciji bilo jednostavnije izvoditi  rimskom nego arapskom notacijom a na specifičan način koji je opisao u članku.

Šikić je odgovorio i Hatzivelkosu. Prema njemu, ne postoji povijesni dokaz da je itko tko se služio rimskim brojkama ikad računao na taj ‘jednostavni’, ‘egipatski’, ‘ruski’, ‘seljački’ način. Šikić dakle ne dovodi u pitanje Hatzvelkosovu demonstraciju jednostavnog ‘egipatskog računanja’ rimskim brojkama, nego tvrdi da nema povijesnih tragova da se to rimskim brojkama ikad tako radilo.

U svoje dvije reakcije Šikić, koji je tridesetak godina predavao povijest matematike na PMF-u u Zagrebu, nije dao eksplicitan odgovor na inicijalno pitanje ‘zašto je arapskim brojkama (koje su toliko efikasnije) trebalo više od pola milenija da zamijene rimske’, nego se usmjerio na opovrgavanje objašnjenja i argumenata Chrisomalisa i Hatzivelkosa.

U prvoj reakciji ima indicija da je njegovo objašnjenje dugotrajnosti zamjene notacije to što se za osnovne matematičke operacije koristio abak. Tako ga je izgleda shvatio i Hatzivelkos, koji ipak misli da abak nije bio u toliko širokoj upotrebi koliko izračun jednostavnih matematičkih zadataka koji je predstavio kao lakši za naučiti i primjenjivati nego računanje arapskim brojkama. Osim toga, korištenjem abaka Chrisomalis ilustrira zaključak da notacija služi prvenstveno reprezentaciji brojeva.

Ako je točno da je abak Šikićevo objašnjenje za dugotrajnost zamjene notacije, onda isti fakt (služenje abakom) Šikić i Chrisomalis tumače drukčije: jedan iz toga izvodi da notacija prvenstveno služi prikazu brojeva i zato je zamjena dugo trajala, a drugi, Šikić, također smatra da zamjena nije bila hitna jer se računalo abakom, ali to ne znači da notacija prvenstveno služi prikazu brojeva. Drugim riječima, objašnjenja i argumenti u svim se člancima i kod svih autora isprepliću i razilaze. Tako je inicijalno pitanje o dugotrajnosti zamjene notacije još otvoreno.

II

Za početak, neka bude prihvaćena Šikićeva tvrdnja da „rimske brojke nikada ne bi dovele do logaritama“. Iz nje ipak ne slijedi da je rimska notacija zamijenjena arapskom radi otkrića logaritama (kako bi bili otkriveni). Da bi tome bilo tako moralo bi se pokazati da su se korisnici rimske notacije suočili s problemom koji su mogli riješiti samo ‘otkrićem’ logaritama i da to nije išlo bez pozicijske notacije[i].K tome, i uz širenje arapske notacije, čak i uz namjeru da se njome omogući rješenje problema koji su riješeni logaritmima, oni nisu morali biti otkriveni, kao što nijedno otkriće nije zadano da se mora dogoditi.

Karen Parshall i Victor Katz u svojoj povijesti algebre pišu o tome da matematičari povijest prikazuju kao logički razvitak. Njih mežutim zanimaju problemi u prošlosti koji su potaknuli razvitak.

Naravno, Šikić nije ni tvrdio da je rimska notacija zamijenjena arapskom radi otkrića logaritama, ali u opservaciji razlike između ‘radi’ i ‘zahvaljujući’ (arapskoj notaciji) radi se ustvari o dva pristupa povijesti matematike. Katz i Parshall[ii] u svojoj povijesti algebre podsjećaju da udžbenici matematička područja uobičajeno prikazuju tako da slijede njihov „logički razvitak“.  U ovoj raspravi o rimskim i arapskim brojkama to bi otprilike izgledalo ovako: uspostavi se pozicijski sustav notacije koji omogući logaritme, na sve se to nasloni kalkulus a zatim „procvjetaju europska matematika i znanost“. Katz i Parshall su, međutim, zainteresirani za „probleme u prošlosti koji su potaknuli razvitak“. Povijest matematike matematičari svode na matematiku, a povijest potiskuju u drugi plan. Ako je, kako Šikić podsjeća, već u Antici, „kad je trebalo efikasno računati“ korišten pozicijski sustav, zašto nije prevladao već nakon Ptolomeja, i zašto su indo-arapskim brojkama trebali mileniji da se rašire svijetom.

Radi izbjegavanja nesporazuma korisno je spomenuti da su oba pristupa povijesti i razvitku matematike – važna. Prvi pristup implicite ili eksplicite prikazuje da je prethodni doseg omogućavao ili čak nužno vodio kasnijem. No, nije se sve moralo dogoditi na način za koji se naknadno ustanovi da je sukladan nekoj unutrašnjoj logici: moglo je biti i drukčije, moglo se odvijati nekim drugim slijedom. Bezbroj je potvrda kontingentnosti u povijesti (i) matematike. Uostalom, upravo onoliko koliko je u svijetu ista i koliko se prožima toliko je u povijesti i u različitim kulturama i civilizacijama matematika i različita.

Drugi je pristup povijesti matematike prizemniji: uz opis što se događalo i kako su se stvari razvijale, istražuje zašto se to baš tako događalo, ne samo s obzirom na kasniji efekt, nego i s obzirom na okolnosti i probleme u vremenu zbivanja. Šikić, na primjer, u vezi sa zamjenom rimske notacije pozicijskom spominje trigonometriju i astronomiju. Na um pada da su bile važne u plovidbi, pomorcima. Ali zamjena notacije nije išla s broda na brod, nije išla morem nego kopnom (kao što će se uskoro vidjeti). Za sam proces presudne su bile trgovina i ekonomija a ne navigacija i astronomija. To su činjenice.

Leonardo iz Pise (Fibonacci) u svojoj je knjizi u kojoj je afirmirao arapske brojke pisao matematiku za trgovce

U njima, u tim se činjenicama razotkrivaju neki uobičajeno zanemareni aspekti prirode matematike. Zato je stvarna povijest matematike važna i za samu matematiku. Drugi pristup izvodi matematiku iz kule bjelokosne i to ne samo promatrajući njezinu primjenu u rješavanju problema, nego i drukčije, recimo prikazom načina bavljenja matematikom i tko se njome bavio. Utoliko je intrigantnije istraživati što se sve dogodilo i zašto su se stvari razvijale upravo onako kako su se razvijale.

U nastavku se prvo kratko opisuje širenje indo-arapske notacije brojeva u Europi. Ta je tema istraživački još vrlo živa, zacijelo upravo zato što je ovaj drugi pristup povijesti matematike sve zanimljiviji.  Šikićeve su primjedbe, međutim, ustvari poticajne. Stoga se dalje raspravlja logika iza Chrisomalisova zaključka da notacija prije služi zapisu veličina nego računanju, a na kraju se otvara i pitanje pozicijskog sustava, sve to ne bi li se potaknulo daljnju diskusiju.

III

Na temelju nekolicine studija[iii] (koje zainteresiranim čitateljima mogu poslužiti za daljnje istraživanje) gruba slika o tome kako su arapske brojke prevladale izgleda ovako. Leonardo iz Pise (Fibonacci) s arapskim se brojevima susreo dok je s ocem boravio u današnjem Alžiru. Otac je bio trgovac i predstavnik trgovaca grada Pise. Fibonacci je 1202 godine objavio Liber Abaci (na linku je knjiga u čitkom engleskom prijevodu sa sadržajnim predgovorom). Fibonacci u prvim poglavljima uvodi arapske brojeve i objašnjava računske operacije pomoću njih, a u kasnijim ih poglavljima primjenjuje na izabrane probleme u ekonomiji, u trgovini, vođenju tvrtke i poslovanju novcem.

Prema nekolicini istraživača u širenju arapskih brojki presudno je bilo njihovo korištenje u ekonomiji (a ne u astronomiji i navigaciji), iako – valja biti pošten – ima i autora koji ne pristaju neupitno uz taj zaključak, nego upućuju na ukupno kulturno okruženje[iv] i ulogu administracije gradova-država[v]. U to se doba matematika poučavala na latinskom u organiziranim školama u sklopu Crkve, također na dvorovima i kasnije sveučilištima, u najboljem slučaju u euklidskoj i platoničko-pitagorejskoj tradiciji[vi]. Bila je to tzv. znanstvena matematika (scholarly mathematics). Organizacija i (znanstveni) interesi administracije (vlade gradova-država) bili su različiti od interesa i autonomne organizacije stanovnika gradova, koji su od 13. stoljeća pokretali privatne škole, na narodnom jeziku, ponajprije za trgovce.  Oslanjale su se najviše na Fibonaccia.

U sljedećih dva stoljeća trgovina talijanskih gradova-država se snažno razvijala kvantitetom i inovacijama. Mjenica (bill of exchange) je omogućila zaobilazno zaračunavanje (zabranjene) kamate na dug putem konverzije valuta i preračunavanja tečaja. Formirane su trgovinske kompanije, koje su prerasle u banke, i transformirale dotadašnji koncept novca. Nezaobilazan je element tog razvoja dvojno knjigovodstvo, kojim je omogućeno formiranje pojma – kapital. Razvija se već od 13 stoljeća, no etablirano je u djelu Summa de arithmetica, geometria, proportioni et proportionalita koje je na talijanskom, potkraj 15 stoljeća objavio Luca Pacioli. Radi se o sintezi i sistematizaciji dotadašnje matematike, prvoj tiskanoj knjizi o algebri napisanoj na talijanskom.

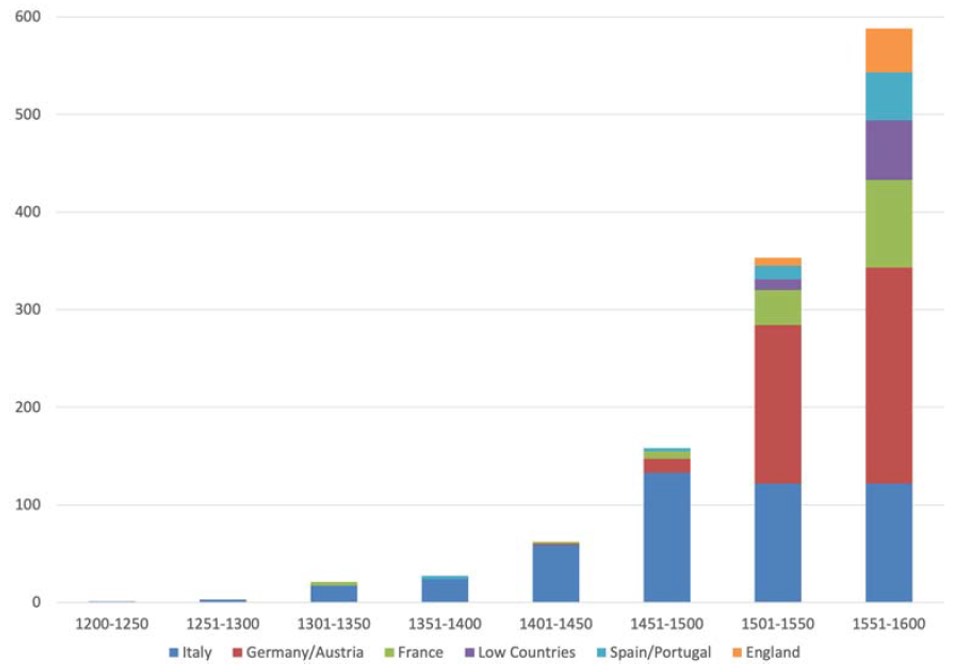
Tijekom tih stoljeća ‘narodnu’ su matematiku poučavali gotovo kao zanat u privatnim školama trgovine. Učitelji u tim školama, ne uvijek sofisticirani matematičari, proizvodili su ono što bi se danas zvalo skripta, priručnici. Bili su  naravno puni grešaka, rezultata bez dokaza, uputa bez objašnjenja. Osim toga, bila je to, iz današnje perspektive, razmjerno nesofisticirana matematika. Raffaele Danna, prema kojem su škole, skripta i trgovina bili glavni kanali širenja indo-arapskih brojeva, proučio je dinamiku njihova objavljivanja. Zamah je izvan Italije osnažen s tiskarskim strojem[vii].

­­

Ukupna proizvodnja praktičnih priručnika iz aritmetike, prema područjima objave.

Potrebno je dodati da se Danna ne bavi otporom prihvaćanju arapskih brojki, ne proučava ‘konkurentske’ škole, priručnike i matematiku u administraciji gradova-država u kojima se i u knjigovodstvu i dalje primjenjivala (i) rimska notacija. I čak je, kao što je spomenuto u prvom članku o Chrisomalisu, u nekim slučajevima u nekim gradovima u poslovnim izviješćima bila zabranjena arapska notacija zbog (lakše) mogućnosti falsificiranja rezultata (pretvaranje nule u osmicu itd.) i nenaviknutosti sredine. Chrisomalis piše da su se arapskom notacijom, koristili „samo obrazovani“ (str. 96), te da su „zapadne brojke bile ograničene na matematičke tekstove, čak na specifičnu vrstu aritmetike u tim tekstovima“ (str. 121). Šikić i Hadživelkos se eksplicite slažu o važnoj ulozi arapske notacije u razvoju matematike. Iz prethodnih citata proistječe da bi i Chrisomalis možda ‘dopustio tu mogućnost’.  Nesporazuma možda i nema. Ipak, podatci koje Danna podastire sugeriraju da je primjena matematike u trgovini, a kojom se Fibonacci velikim dijelom bavi u svojoj knjizi, imala snažan utjecaj na širenje arapskih brojki. Pitanje je zašto su arapske brojke bile prikladnije nego dotadašnje računanje, na abaku i zapisivanje rimskom notacijom?

IV

Da nije bilo Šikićeve reakcije na Chrisomalisa u ovom je nizu članaka o matematici i brojevima sljedeća trebala biti predstavljena knjiga The Materiality of Numbers: Emergence and Elaboration from Prehistory to Present (Cambridge University Press, 2023). u kojoj se kognitivna arheologinja Karenleigh Overmann bavi nastankom i prirodom brojeva. Autoričina je glavna teza da su u formiranju brojeva nezaobilazna ‘materijalna sredstva’ (material devices) u koja izrijekom uvrštava: prste, raboš (tally), razne vrste ‘tokena’ (kamenčići, žetoni, čak i novčići), abak, abacus (računaljke raznih oblika) i – numeričke notacije. Neka od tih sredstava prvenstveno služe akumulaciji (raboš, z-brojanice) i grupiranju (kamenčići, žetoni), druga računanju, treća bilježenju i predstavljanju broja kao veličine itd.

U istraživanju zamjene rimskih brojeva arapskima nužno je imati u vidu abak, koji nedvojbeno služi računanju. Povijest abaka duga je više tisuća godina[viii] i za to je vrijeme imao vrlo različite oblike. Danas je najpoznatiji abak u obliku računaljke kakvih još ima u školama ili ih se može u dućanima s igračkama kupiti da se djeca uče računanju. Često je riječ o kutiji u kojoj su osovine duž kojih se pomiču kuglice. Jedna je osovina za jedinice, na sljedećoj kuglice označavaju pet ili deset puta veći broj. Kad se na prvoj osovini zbroji 2+2 pomaknu se četiri kuglice, doda li se još jedna prijeđe se na sljedeću osovinu a jedinične se kuglice vrate na početnu poziciju. Abak je bio crtan u pijesku ili prašini a na linije su postavljani kamenčići. (Prema jednoj teoriji čak i ime abacus potječe od prašine[ix]. No, ta teorija, iako često spominjana, ima i svoje stroge oponente.[x]) Prenesen je na ploču, odnosno stol za računanje (counting board) i u tom se obliku najčešće spominje u kasnom Srednjem vijeku i ranoj Renesansi u vrijeme procesa zamjene rimskih brojeva arapskima. Uglavnom je ta ploča, stol, postojala u trgovinskim središtima i na mjestima za trgovanje i trgovci ga, koliko se može razabrati iz materijala, nisu prenosili od grada do grada. Zanimljivo, Exchequer, svojevrsno ministarstvo financija u Britanskoj vladi, ime duguje ploči na kojoj su se računali prihodi i rashodi.

Na abaku se, o kojemgod njegovom obliku bila riječ, prenosivom ili neprenosivom, moglo računati a da se rezultat (veličina) zapisuje rimskim brojkama. Načelno govoreći, rezultat se mogao zapisivati i arapskim brojkama, ali na odgodu preuzimanja arapske notacije utjecala je, kao što je napomenuto, navika, a i transparentnost rimskih brojki (koje je spominjao Hatzivelkos): kad se rimskim brojkama napiše III očito je to broj tri, a kad se napiše arapskim to nije očito, mora se naučiti. Upravo je o tome ovdje riječ, o materijalnim karakteristikama sredstava numeracije.

Razvijeni abak vrlo je efikasno sredstvo za računanje. I Chrisomalis i Šikić spominju abak u Kini i Japanu na kojem su oni koji su se njime vješto služili računali brže i točnije nego oni koji su se služili strojevima za računanje, a kamoli brže od onih koji su računali na papiru[xi]. Ipak, efikasnost japanskog abaka u odnosu na računanje olovkom na papiru, nema veze sa zamjenom rimskih brojki arapskima.

Međukoraci računanja na abaku iščezavaju i ne ostaju zabilježeni. Vidljiv je samo rezultat

Stvar je u tome da međukoraci računanja na abaku iščezavaju i ne ostaju zabilježeni (kao što iščezavaju na većini kalkulatora). Vidljiv je samo rezultat. Trgovcima je, naravno, vrlo važna transparentnost računa, radi kasnije provjere. To je ta ključna materijalna karakteristika/prednost računa na papiru. Raffaele Dana to formulira riječima da je zapis računanja olovkom na papiru omogućavao provjeru točnosti a da se ne ponavlja cijela procedura[xii]. U ovom kontekstu Chrisomalisova tvrdnja da notacija (u usporedbi s abakom) služi prvenstveno za bilježenje veličina, izgleda manje pogrešna. To je ne čini ni potpuno istinitom, ali jedna je od poanti ovog članka da o historiji i nema potpune istine.

Overmann inzistira na tim materijalnim karakteristikama numeričkih sredstava, koja dijeli ugrubo na ona koja služe bilježenju i ona koja služe manipulaciji. Notacije su fiksne, stoga se računati mora drukčije (na prste, na abaku), sve dok se na papiru ne počnu zapisivati i koraci računanja, naglašava Overmann. Algoritam računanja na papiru se također razvijao. Kad Fibonacci objašnjava računske operacije arapskim brojkama za pamćenje međukoraka koristi se ‘rukama’ (prstima). Kod množenja 37×37, koji je jedan od njegovih primjera, prvo se pomnoži 7×7=49, zatim se 9 zapiše na odgovarajuće se mjesto, a 4 se ‘zapamti rukama’[xiii].

­­

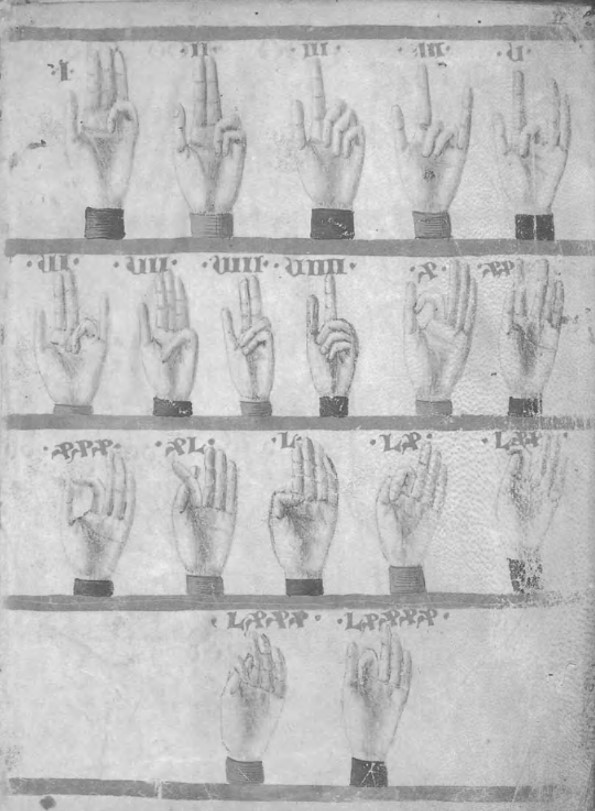
Prsti se kod Fibonaccija još koriste kod računanja. Činjenica je (stvarnost je) da su se algoritmi koji nisu zahtijevali pomoćno sredstvo za računanje (poput prstiju ili računaljki) razvili u okviru arapske pozicijske decimalne notacije, posebno za složenije operacije većim brojevima.

V

Šikić naglašava kako je indo-arapska notacija pozicijski sustav a rimska nije. To, načelno, nije sporno. Chrisomalis rimsku notaciju klasificira kao kumulativno aditivnu. Za razliku od pozicijske, u kojoj je slijed potencija baze zadan, u rimskoj se notaciji 1233 može napisati uobičajeno – MCCXXXIII, ali i drugim, obratnim redoslijedom – IIIXXXCCM, pa čak i nekim trećim redom. Iako se uglavnom koristio i koristi prvi redoslijed, u kojem potencije baze idu od veće prema manjoj, kao kod babilonske notacije (vidi sliku iz Chrisomalisove knjige). Svakodnevni je korisnik rimske notacije, objasnio je Hatzivelkos u svojoj reakciji, mogao jednostavno zbrajati jedinice, desetice itd koje su mu prepoznatljive same po sebi. Arapska i grčka alfabetska notacija su ‘šifrirane’. Ne samo da se moralo naučiti koji znak označava koji broj nego se i računati moralo ‘napamet’, a ne brojanjem, kumulacijom.

­­

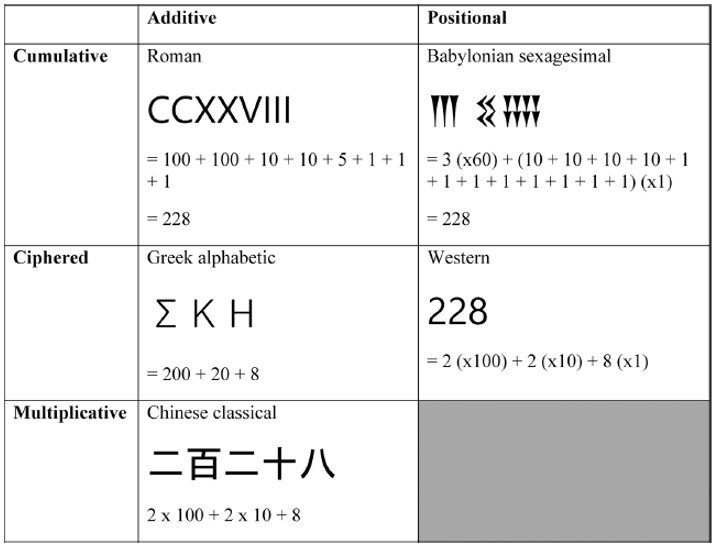
Kod kineskog se sustava potencije baze – stotice, desetice ne pišu pojedinačno, kao kod rimskog, ne dodaju se jedna drugoj nego se pomnože: 200 se ne piše CC (C+C), nego 2×100. No to također znači da je broj u kineskom sustavu mogao biti zapisan i drugim redoslijedom, kao i u rimskoj notaciji, iako su potencije baze uglavnom pisane od veće prema manjoj. U indo-arapskom sustavu je potencija baze na fiksnoj poziciji, nije neobavezna, a – kao kod kineskog sustava – množi se cifrom (šifrom), brojkom.

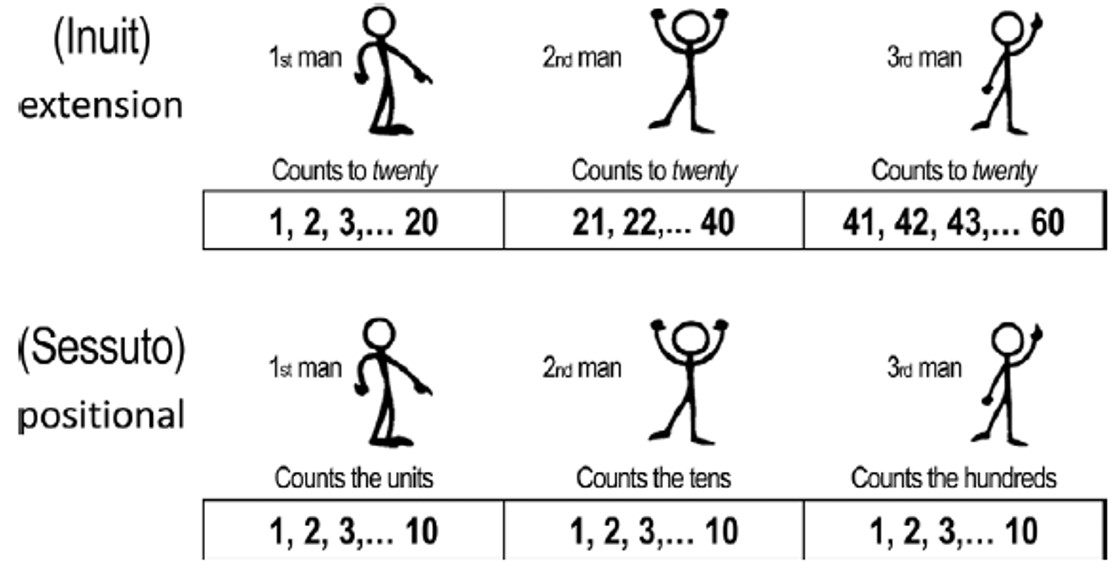
S jedne je strane arapski pozicijski sustav zahtijevao višu razinu apstrakcije, kao što piše Hatzivelkos, a s druge je strane on očito ishod jednog razvitka. Dosad je taj razvitak opisom Chrisomalisove klasifikacije notacija samo natuknut. U 9. poglavlju pod naslovom Making Quantity Tangible and Manipulable Overmann spominje afričko pleme Sessuto (ili Sesotho) koje broji prstima ali se koristi pozicijskim sustavom. Kad prvi čovjek prstima odbroji nečega deset, onda drugi čovjek digne jedan prst a prvi nastavi brojati. Kad drugi ‘potroši’ svih deset prsta za desetice, treći koji broji stotice podigne jedan prst. Kod kanadskog plemena Inuit također se surađuje u brojanju prstima, ali kad prvi potroši svih dvadeset prsta s ruku i nogu, sljedeći kreće sa svojim prvim prstom do broja četrdeset i tako dalje. Taj sustav očito nije pozicijski, za razliku od sustava Sessuto plemena.

­­

I abak je pozicijski, samo je često sa podbazom pet: kad se zbroje četiri kuglice prelazi se na sljedeću osovinu, ili kad ih se zbroji devet. Iako je Fibonacci najznačajniji za afirmaciju arapske numeracije, već prije njega, u 10. stoljeću benediktinac Gerbert (kasnije papa Silvester II) preuzeo je cifre od 1 do 9 i njima označio stupce na abaku. U indo-arapskom pozicijskom sustavu važna je i nula. U Babilonu, nula nije pisana nego je pozicija bila prazna, kao i u nekim kineskim sustavima, ali se oznaka za ‘ništa’ ipak počela upisivati otprilike u isto doba, u 7. stoljeću, kad se pojavljuje u Indiji i kad su također  objašnjene četiri osnovne operacije s nulom[xiv]. Uvođenje nule često se predstavlja kao misaoni skok, takozvani ‘epistemički rez’. Izbliže se vide faze tog ‘misaonog skoka’ koji je trajao tisućljećima. Čini se nedvojbenim da su u rimsko su doba poznavali razlomke koje su računali u dvanaestičnom sustavu, ali istraživači nisu sigurni kako su ih točno računali. Fibonacci se koristio takozvanom složenim razlomcima. Na primjer složeni razlomak značio je, što je naravno 29/30. Tek je Nizozemac Simon Stevin potkraj 16. stoljeća uveo decimalnu točku. Na Wall Streetu, newyorskoj burzi, cijene su se do 2001. godine, u skladu sa španjolskom trgovinskom tradicijom mogle isticati samo u razlomcima, do razine šesnaestine kad je usvojen decimalni sustav.

Dva su cilja ovog nasumičnog nabrajanja komponenti ugrađenih u decimalni pozicijski sustav. Prvo, lako se složiti sa Šikićem da pitanje notacije nije beznačajno, inače promjena/usavršavanja ne bi ni bilo. Slijedi to i iz Overmann, koja naglašava materijalnost ideje broja, a u materijalna sredstva uvrštava i notaciju: drugim riječima, u rimskoj i arapskoj notaciji različit je i koncept broja. To je ipak vrlo apstraktan zaključak i otvoren diskusiji: nije lako odbaciti predodžbu da se isti ‘platonovski’ brojevi jednostavno ‘transliteriraju’ iz jedne u drugu notaciju.

Iz prikazanog faznog razvoja pozicijskog sustava nameće se konkretnije pitanje: Ako se tvrdi da su logaritmi mogli biti otkriveni tek nakon konstrukcije decimalnog pozicijskog sustava – u kojem je to trenutku točno postalo moguće, koja je to točno komponenta omogućila, koja je bila presudna i zašto?

Drugo, u razvoju je sudjelovala i rimska notacija. Fibonacci se u svom kasnijem djelu Liber Quadratorum iz 1225 kod nekih problema koristi rimskim brojkama[xv].  U prvom članku u ovoj raspravi spomenuto je da je Ocreatus početkom 12. stoljeća dodao nulu u rimsku notaciju na prazno decimalno mjesto, ali se to njegovo usavršavanje nije primilo. Vjerojatno je za decimalni pozicijski sustav ipak nužno šifrirati brojke. Overmann kroz cijelu knjigu nastoji pokazati da su se kasniji sustavi brojeva nastavljali na prethodne, a mijenjani su kad je složenost društva postavljala zadatke koje nije bilo moguće riješiti dotadašnjim sustavom. U tim generalnim zaključcima preostaje još praznih mjesta za ispuniti detaljima razvoja koncepta broja, notacije i materijalnih sredstava.

• Bilješke

[i] Ovdje možda nije suvišno podsjetiti da je Li Shanlan kreirao logaritme o okviru kineske matematičke tradicije. Doduše, bio je prevodilac zapadne matematike na kineski, što može biti objašnjenje njegove ideje da se uopće bavi logaritmima, ali usporedo s upoznavanjem zapadne razvijao je i tradicionalnu kinesku matematiku. Otvoreno je dakle pitanje jesu li logaritmi mogli biti otkriveni i u sklopu neke matematičke tradicije s drukčijom notacijom. Prijevodi iz jedne u drugu notaciju logaritamskih i trigonometrijskih tablica bili su vrlo živi tijekom povijesti. Koliko, i još više, u čemu, kako, notacija utječe na razvoj matematike pitanje je za detaljnu analizu.

[ii] Victor J. Katz and Karen Hunger Parshall, 2014: Taming the Unknown: A History of Algebra from Antiquity to the Early Twentieth Century; Princeton University Press

[iii] Najnoviji su, i zahvaljujući tome i najinformativniji, članci koje je napisao Raffaele Danna, koji je na temi širenja indo-arpaskih  brojeva recentno doktorirao na Oxfordu a trenutačno je postdoktorand na European University Institute. Često je tako da su recentni doktorati odličan izvor, jer doktorski student ima obavezu proći kroz sav materijal, sistematizirati ga i sintetizirati. Ovdje upućujem na dva članka – Raffaele Danna, 2021: Figuring Out: The Spread of Hindu-Arabic Numerals in the European Tradition of Practical Mathematics (13th–16th Centuries); Nuncius, Journal of the Material and Visual History of Science; te The spread of Hindu-Arabic numerals among practitioners in Italy and England (13th-16th c.): two moments of a European innovation cycle?, objavljen kao poglavlje u knjizi The knowledge economy: innovation, productivity and economic growth, 13th to 18th century, kojoj je urednik Giampiero Nigro (Firenze University Press, 2023). Ostale se njegove članke, na istu temu, može naći na Google Scholar Citations Raffaele Danna. S autorom sam stupio u kontakt i dao mi je korisne naputke.

[iv] John W. Durham, 1992: The Introduction of ‘Arabic’ Numerals in European Accounting;, The Accounting Historians Journal ne prihvaća svođenje širenja arapskih brojeva na njihovo  korištenje u ekonomiji.

[v] Alexander Murray, 1978: Reason and Society in the Middle Ages; Oxford University Press. O raspravi s Murrayem vidi. Stephen E. Sachs: New Math:The ‘Countinghouse Theory’ and the Medieval Revival of Arithmetic

[vi] Charles Burnett, 2013: The Twelfth-Century Renaissance, The Cambridge History of Science, Vol. 3, Medieval Science, ur. David C. Lindberg  and Michael H. Shank;

Maria Pia Maraghini 2011; The role of the ‘abacus tradition’ for the economic and social development of the society: evidence from Tuscany (Italy) between XIII and XVI century;  Pecvnia, Revista de la Facultad de Ciencias Economicas y Empresariales, Universidad de Leon

[vii] U istom duhu o širenju arapskih brojeva piše Maraghini te na primjeru Britanije i Nizozemske Eric Aerts, 2023:  Hindu-Arabic Numerals in Public and Private Accounts of the Southern Low Countries (1300-1800) The Journal of European economic history; Vol. 57; iss. 2; pp. 33 – 50

[viii] Keith F. Sugden, 1981: A History of the Abacus;, The Accounting Historians Journal

[ix] Williard E. Stone, 1972: Abacists versus Algorists, Journal of Accounting Research

[x] Durham, ibid

[xi] U uvodu knjizi The Universe in Zero Words: The Story of Mathematics as Told through Equations (Princeton University Press, 2012) Dama Mackenzie opisuje zabavnu epizodu natjecanja nobelovca za fiziku Richarda Feynmana sa stručnjakom za računanje na abakusu, koja je ovdje dostupna na internetu.

[xii] Danna, 2021, ibid.

[xiii] Na samom početku Fibonaccijeve knjige i prije spomenutog prijevoda je slika kako su se brojevi pamtili rukama. Također, primjer množenja 37×37  u kojem Fibonacci upućuje na ‘pamćenje rukama’ jedan je od prvih u knjizi i lako se nađe tražilicom.

[xiv] Franka Miriam Bruekler, 2022: Povijest matematike, PMF Zagreb

[xv] Katz i Parshall, ibid, str. 185.