Zaključivanje u prirodnom i artificijelnom jeziku. Od Aristotela prema Fregeu

U prvom nastavku serijala o logici, Zvornimir Šikić predstavlja njene temeljne forme, definicije i teoreme, te pokazuje kako je apstrahiranje formi iz prirodnih jezika logiku čvrsto vezalo uz njihovu sintaksu.

• Naslovna fotografija: Starogrčki filozof i prirodoslovac Aristotel

• Što je logika

Osnovna tema logike su argumenti i njihova valjanost. Razmotrimo sljedeći argument:

Zagreb je u Hrvatskoj ili je u Sloveniji. Zagreb nije u Hrvatskoj.

Dakle, Zagreb je u Sloveniji.

Taj argument sadrži dvije premise i konkluziju. Preglednije ćemo ga zapisati tako da premise crtom odvojimo od konkluzije i sve tvrdnje numeriramo.

\(
\begin{array}{l}
\text{(1) Zagreb je u Hrvatskoj ili je u Sloveniji.} \\
\text{(2) Zagreb nije u Hrvatskoj.} \\
\hline
\text{(3) Zagreb je u Sloveniji.}
\end{array}
\)

Konkluzija ovog argumenta nije istinita, a nisu istinite ni sve njegove premise. Premisa (1) je istinita, a premisa (2) nije. Ipak, ovaj argument je valjan. Zašto? Zato što ima valjanu formu:

\(
\begin{array}{l}
\text{(F1) P ili Q} \\
\text{(F2) Nije P} \\
\hline
\text{(F3) Q}
\end{array}
\)

Ta forma je valjana jer svaka interpretacija (od P i Q) koja premise čini istinitima i konkluziju čini istinitom.

Uočimo da naš konkretni argument (1)(2)/(3) logički valjanim čini njegova logička forma (F1)(F2)/(F3). Zato je ključna zadaća logike otkriti formu argumenta koji nas zanima i utvrditi je li ona valjana.

Tisućljetna je tradicija da se logičke forme apstrahiraju iz prirodnih jezika, kao u gornjim primjerima. To je logiku čvrsto vezalo uz sintaksu prirodnih jezika. Pogledajmo još neke primjere.

\(
\begin{array}{l}
\text{(4) Nijedan logičar nije zao.} \\
\text{(5) Neki Hrvati su logičari.} \\
\hline
\text{(6) Neki Hrvati nisu zli.}
\end{array}
\)

Aristotel, i mnogi drugi poslije njega, apstrahirali su sljedeće forme iz premisa (4), (5) i konkluzije (6):

\(
\begin{array}{l}
\text{(A4) Nijedan M nije P.} \\
\text{(B4) Neki S su M.} \\
\hline
\text{(F4) Neki S nisu P.}
\end{array}
\)

Matematički orijentirani Boole apstrahirao je jednadžbe i nejednadžbe:

\(
\begin{array}{l}
\text{(B4) } M \cdot P = 0 \\
\text{(B5) } S \cdot M \neq 0 \\
\hline
\text{(B6) } S \cdot \overline{P} \neq 0
\end{array}
\)

Frege je, u okviru mnogo šireg projekta formalizacije logike koja se koristi u matematici (i konačne redukcije matematike na logiku) došao do sljedećih formi:

\(
\begin{array}{l}
\text{(F4) } \forall x (M(x) \rightarrow P(x)) \\
\text{(F5) } \exists x (S(x) \land M(x)) \\
\hline
\text{(F6) } \exists x (S(x) \land \neg P(x))
\end{array}
\)

Bitna novost Booleovog i Fregeovog pristupa jest da oni, obojica inspirirani sličnim postupcima u matematici, definiraju beskonačne skupove formi neovisno od toga jesu li one forme iskaza prirodnih jezika. Drugim riječima, oni definiraju artificijelne formalne jezike. U tako definiranim formalnim jezicima mogu se egzaktno definirati postupci za utvrđivanje valjanosti formalnih argumenata. Tada neformalne argumente smatramo valjanima tek ako su oni konkretne interpretacije valjanih formalnih argumenata.

Slijedeći ovu tradiciju logičke teorije razvijaju se u tri koraka.

(I) Definiraju se forme i njihove interpretacije te što znači da je forma istinita u nekoj interpretaciji. Stručnije kazano definira se sintaksa i semantika formalnog jezika logike. Naravno, razne logike određene su raznim formalnim jezicima. Uočimo, nadalje, da je interpretacija forme uvijek istinita ili neistinita tj. uvijek ima jednu od dvije vrijednosti: istinu koju označavamo s ⊤ ili neistinu koju označavamo s ⊥. Dakle, interpretacija forme u prirodnom jeziku uvijek će biti deklarativna rečenica (izjava, sud, tvrdnja), a ne pitanje, uzvik, naredba, molba ili neki drugi iskaz koji po svom značenju nije ni istinit ni neistinit. (U tom smislu su formalni jezici, kojima se bavi logika, siromašniji od prirodnih jezika.)

(II) Definiraju se ključni logički pojmovi: implikacija, ekvivalencija, konzistentnost, valjanost (logička istinitost) itd. Te su definicije iste za sve formalne jezike, tj. za sve logike pa ih odmah iskazujemo.

DEFINICIJA IMPLIKACIJE

Forme A, B, C, . . . koje zovemo premisama, impliciraju formu K koju zovemo konkluzijom, ako je konkluzija K istinita u svakoj interpretaciji u kojoj su istinite sve premise A, B, C, . . . . Zapisano simbolima: A,B,C,…⇒ K.

DEFINICIJA KONZISTENTNOSTI

Forme A, B, C, . . . su međusobno konzistentne ako postoji interpretacija u kojoj su sve one istinite. Zapisano simbolima: ⟐(A,B,C,…).

DEFINICIJA VALJANOSTI (LOGIČKE ISTINITOSTI)

Forma A je valjana (logički istinita) ako je istinita u svakoj interpretaciji. Zapisano simbolima: ⊡A.

DEFINICIJA EKVIVALENCIJE

Forme A i B su međusobno ekvivalentne ako u svakoj interpretaciji imaju istu vrijednost istinitosti. (To znači da A implicira B i B implicira A). Zapisano simbolima: A ⇔ B.

Uočimo da ove definicije pretpostavljaju da je već obavljen I. korak, tj. definirane su forme i njihove interpretacije te što znači da je forma istinita u interpretaciji.

Ovi ključni pojmovi su interdefinabilni. Na primjer, premise A, B, C, . . . ne impliciraju konkluziju K akko (ako i samo ako) postoji interpretacija u kojoj su sve premise istinite, a u kojoj konkluzija ipak nije istinita. No to znači da postoji interpretacija u kojoj su istinite sve premise A, B, C, . . . i negacija konkluzije K.

TEOREM O VEZI IMPLIKACIJE I KONZISTENTNOSTI

Premise A, B, C, . . . impliciraju konkluziju K akko su forme -K, A, B, C, . . . međusobno inkonzistentne. Zapisano simbolima: A,B,C,…⇒K akko -⟐(-K,A,B,C,…).
Slično, forma nije konzistentna akko je neistinita u svim interpretacijama, što znači da je njezina negacija valjana.

TEOREM O VEZI VALJANOSTI I KONZISTENTNOSTI

Forma F je valjana akko njezina negacija F nije konzistentna. Zapisano simbolima:

⊡ A akko – ⟐-A.

(III) U trećem koraku izgradnje logike definiraju se algoritmi uz pomoć kojih je moguće testirati implikaciju, ekvivalenciju, konzistentnost, valjanost itd. Za neke logike ti algoritmi postoje, a za neke se dokazuje da ne postoje.

Sve definicije i dokazi opisani u ova tri koraka provode se matematički egzaktno. S druge strane, primjena tako izgrađene matematičke logike neće biti matematički egzaktna ako takav nije predmet njene primjene (što sigurno nije svakodnevna argumentacija).

Kao i uvijek, primjena matematičke teorije posebno je umijeće. U našem slučaju posebno je umijeće neformalni argument iz prirodnog jezika pretvoriti u konkretnu interpretaciju odgovarajućeg formalnog argumenta (koji se tada koristi u analizi početnog neformalnog argumenta).

Neformalni argumenti (1)(2)/(3) i (4)(5)/(6) bili su u tom smislu krajnje jednostavni, ali nije uvijek tako. Promotrimo sljedeći argument:

\(
\begin{array}{l}
\text{(7) Ako su svi odbijeni kandidati VKV, onda neki kandidati nisu odbijeni.} \\
\text{(8) Ili su svi kandidati odbijeni ili su svi kandidati VKV.} \\
\hline
\text{(9) Ako su svi VKV kandidati odbijeni onda neki kandidati koji nisu VKV jesu odbijeni.}
\end{array}
\)

Taj je argument valjan iako su izuzetno rijetki oni koji to odmah vide. On je konkretna interpretacija formalnog bulovskog argumenta koji je dokazivo valjan pa tek to dokazuje valjanost konkretnog argumenta. To je tipični primjer uspješne primjene formalne logike na neformalnu argumentaciju.

S druge strane postoje trivijalni neformalni argumenti, koje svi i odmah prepoznaju kao valjane, a čija je matematizirana logička forma dosta složena.

Promotrimo argument:

\(
\begin{array}{l}
\text{(10) Sve elipse su krivulje.} \\
\hline
\text{(11) Svi crtači elipsa su crtači krivulja.}
\end{array}
\)

Argument je očito valjan, iako nema bulovske forme koja bi to dokazala. To se dokazuje tek u bitno složenijoj Fregeovoj formalizaciji. Neki to smatraju nedostatkom formalizacija koje su se udaljile od prirodnih jezika i traže formalizacije koje su mu bliže, a neki pak stvarnom složenošću koja se krije duboko ispod katkada samo prividno jednostavne površine prirodnog jezika.

Današnja logika slijedi Boole-Fregeovu tradiciju matematizirane logike koja vezu s neformalnim argumentima prirodnih jezika tumači kao primjenu formalne matematičke teorije. To ne znači da se uvođenje mnogih logičkih pojmova ne motivira baš pomoću njihovih primjena. Dapače, to je još uvijek najbolja metoda poduke bilo koje matematičke teorije pa tako i matematičke logike.

Sve prethodno kazano ilustrirat ćemo na primjeru logike istinosno funkcionalnih formi, koja se zove i logikom sudova.

• Istinosno funkcionalni veznici

Svi prirodni jezici sadrže veznike pomoću kojih se iz jednostavnijih deklarativnih rečenica grade složenije. Neki od tih veznika su istinosno funkcionalni, što znači da je vrijednost istinitosti složene rečenice jednoznačno određena vrijednostima istinitosti komponenti koje su vezane tim veznikom. (Drugim riječima, vrijednost istinitosti složene rečenice funkcija je vrijednosti istinitosti njezinih komponenti; otuda termin “istinosno funkcionalni”.) Na primjer, binarni veznici “i”, “ili”, kao i unarni operator “nije” (koji ćemo radi jednostavnosti također zvati veznikom), u hrvatskom su jeziku najčešće istinosno funkcionalni. U logici ih nazivamo konjunkcijom, alternacijom i negacijom, a označavamo ih simbolima ∧,∨ i -.

Sljedeće tablice istinosnih vrijednosti definiraju kako vrijednosti istinitosti konjunkcije P ∧ Q, alternacije P ∨ Q i negacije –P (koju još zapisujemo \(\small \overline{P}\)) ovise o vrijednostima istinitosti njihovih komponenti P i Q, odnosno P.

DEFINICIJA KONJUNKCIJE ∧ ALTERNACIJE ∨ I NEGACIJE –

­­

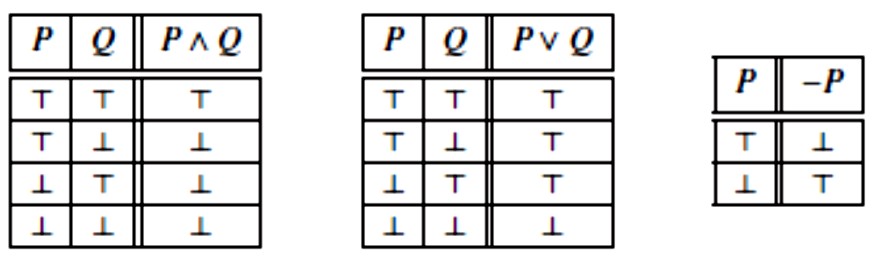
Mnogi veznici prirodnih jezika nisu istinosno funkcionalni (ili katkad to jesu, a katkada nisu). Na primjer, binarni veznik “jer”, kao ni unarni veznici “nužno je” i “moguće je”, očito nisu istinosno funkcionalni.

­­

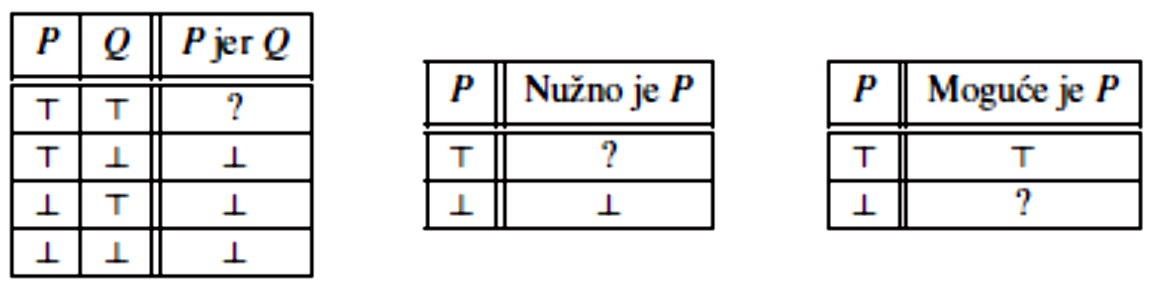
Naime, čak i ako je istina da je Ivan umro (P = ⊤) i da je prije smrti pojeo sladoled (Q = ⊤), to ipak ne znači da je Ivan umro jer je pojeo sladoled (P jer Q = ⊤); možda je doživio infarkt (P jer Q = ⊥). Nadalje, neke faktične istine su nužne, a neke nisu. “Nužno je 2+2 = 4” je istina, ali “Nužno je bilo da Zemlja ima samo jedan prirodni satelit” nije. Slično, neke bi faktične neistine mogle biti istinite, a neke ne bi. “Moguće je bilo da Zemlja nema samo jedan prirodni satelit ” je istina, ali “Moguće je da je 2 + 2 ≠ 4” nije.

Logika istinosno funkcionalnih formi ograničava se samo na istinosno funkcionalne veznike i time je ograničena u odnosu na prirodne jezike. S druge strane, prirodni jezici sadrže mali broj veznika (dakle, i mali broj IF–veznika), dok IF–logika uključuje sve moguće IF–veznike, tj. sve unarne, binarne, ternarne, itd. funkcije koje sklopovima istinosnih vrijednosti pridružuju ⊤ ili ⊥.

Sve unarne istinosne funkcije definirane su sljedećim tablicama:

­­

Ukupno ih je 4. Prva je konstanta ⊤ (f₁ (P) = ⊤), druga je identitet (f₂ (P) = P), treća je negacija (f₃ (P) = –P) i četvrta je konstanta ⊥ (f₄ (P) = ⊥). Binarnih istinosnih funkcija ima 16 (dvije od njih su konjunkcija i alternacija). Ternarnih ima 256 itd. Dakle, istinosnih funkcija ima beskonačno mnogo. Ipak, sve se one mogu realizirati pomoću samo tri: konjunkcije ∧, alternacije ∨ i negacije −.

Promotrimo, na primjer, jednu od 256 ternarnih istinosnih funkcija F (P, Q, R) koja je zadana sljedećom tablicom istinosnih vrijednosti (lijeva tablica):

­­

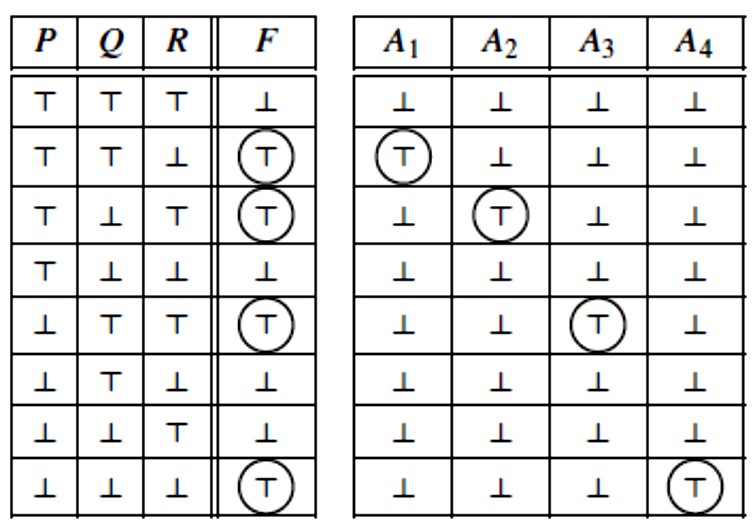
Funkcija F (P, Q, R) jednoznačno određuje funkcije A_i (P, Q, R) koje imaju samo po jednu vrijednost ⊤ i to na točno onim argumentima na kojima F (P, Q, R) prima vrijednost ⊤. Dakle, koliko puta F primi vrijednost ⊤ toliko imamo funkcija A_i, u našem slučaju 4. Te su funkcije također prikazane u gornjoj tablici desno. Iz definicije funkcija A_i odmah slijedi

\(
F(P,Q,R)= A_1 (P,Q,R) \vee A_2 (P,Q,R) \vee A_3 (P,Q,R) \vee A_4 (P,Q,R) \tag{1}
\)

Osim toga, očito je da konjunkcija P ∧ Q ∧ -R prima vrijednost ⊤ isključivo na argumentu (⊤,⊤,⊥), konjunkcija P ∧ -Q ∧ R isključivo na argumentu (⊤,⊥,⊤), konjunkcija -P ∧ Q ∧ R isključivo na (⊥,⊤,⊤), a -P ∧ –Q ∧ -R isključivo na (⊥,⊥,⊥). To znači da vrijedi

\(
A_1 = P \land Q \land \neg R \quad A_2 = P \land \neg Q \land R  \quad A_3 = \neg P \land Q \land R  \quad A_4 = \neg P \land \neg Q \land \neg R \tag{2}
\)

Iz (1) i (2) slijedi

\(
F(P,Q,R) = (P \land Q \land \neg R) \vee (P \land \neg Q \land R) \vee (\neg P \land Q \land R) \vee (\neg P \land \neg Q \land \neg R) \tag{3}
\)

tj. F je konačno realizirana pomoću konjunkcija ∧, alternacija ∨ i negacija -. Specifični oblik (3) kojim je predstavljena naša funkcija F zove se potpuna alternacijska normalna forma, a iz naše analize slijedi da se svaka istinosna funkcija može prikazati pomoću konjunkcije ∧, alternacije ∨ i negacije – u potpunoj alternacijskoj normalnoj formi.

(Da smo krenuli od formi K_i (P, Q, R) koje imaju samo po jednu vrijednost ⊥ i to na točno onim argumentima na kojima F (P, Q, R) prima vrijednost ⊥, analogno bismo zaključili da je F (P, Q, R) = K₁ (P, Q, R) ∧ K₂ (P, Q, R) ∧ K₃ (P, Q, R) ∧ K₄ (P, Q, R) te da su forme K₁=-P ∨ -Q ∨ -R, K₂=-P ∨ Q ∨ R, K₃=P ∨ -Q ∨ R, K₄=-P ∨ Q ∨ -R. To bi bila potpuna konjunkcijska normalna forma početne forme.).

Ekvivalenciju, označenu s ⇔, definirali smo sasvim općenito u 1. odjeljku. U ovom posebnom IF–kontekstu ekvivalentnost dvaju IF–formi znači jednakost IF–funkcija koje one definiraju. Na primjer, funkcije definirane formama \(\small \neg (P \land Q)\) i \(\small \overline{P} \vee \overline{Q}\) su jednake, što lako slijedi iz jednakosti njihovih tablica istinitosti:

­­

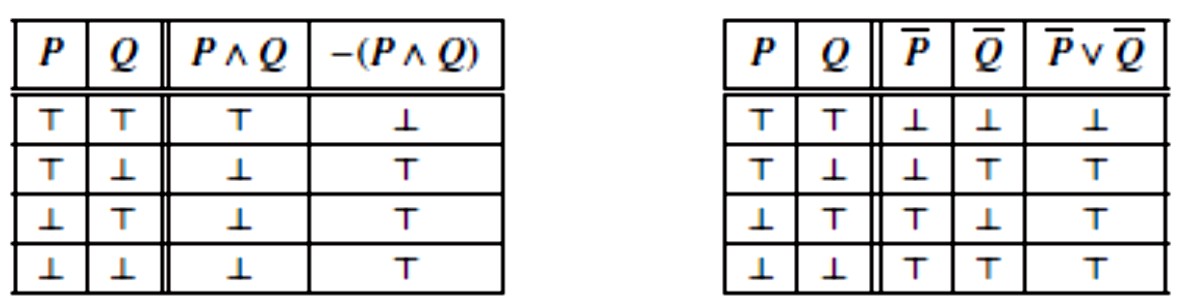
Uobičajeno je konjunkciju P ∧ Q kraće zapisati kao PQ. Osim toga konjunkcije i alternacije s više od dvije komponente, pišemo bez zagrada. Na primjer, (PQ)R i P(QR) kraće pišemo PQR (naime, (PQ)R⇔P(QR)).

De Morganovi zakoni, \(\small P \land Q \Leftrightarrow \neg (\overline{P} \vee \overline{Q})\) i \(\small P \vee Q \Leftrightarrow \neg (\overline{P} \land \overline{Q})\), omogućuju da se osnovni skup IF–veznika {∧,∨,-} koji generira sve IF–veznike, reducira na još manje skupove generatora, {∧,-} ili {∨,-}. Dapače, veznik ↓ definiran s \(\small P \downarrow Q \Leftrightarrow \overline{P} \land \overline{Q}\) (ni P ni Q) generira {∧, −} jer očito vrijedi:

\(\small P \downarrow P \Leftrightarrow \overline{P} \land \overline{P} \Leftrightarrow \overline{P} \quad \quad \overline{P} \downarrow \overline{Q} \Leftrightarrow \overline{\overline{P}} \land \overline{\overline{Q}} \Leftrightarrow P \land Q\)

Takav IF–veznik, koji generira sve moguće IF–veznike, zovemo Schefferovim, jer je Sheffer prvi našao takav veznik. Post je dokazao sljedeći opći teorem koji karakterizira Shefferove veznike.

POSTOV TEOREM O SHEFFEROVIM VEZNICIMA

Istinosno funkcionalni veznik F (P, Q,…,R) je Shefferov akko

\(\small F(P, Q, \ldots, R) \neq \neg F(P, Q, \ldots, R)\) i \(\small F(P, P, \ldots, P) = \overline{P}\).

• Forme, interpretacije i istinitost

Naš opći plan matematički egzaktnog razvijanja logičkih teorija sada ćemo primijeniti na istinosno funkcionalnu logiku (tj. na logiku sudova).
Prvi je korak definicija istinosno funkcionalnih formi. Naravno, gradimo ih uz pomoć istinosno funkcionalnih veznika, a možemo se ograničiti na bilo koji skup IF–veznika koji generira sve IF–veznike.

DEFINICIJA ISTINOSNO FUNKCIONALNE FORME (IF–FORME)

Ako neki skup IF–veznika generira sve IF–veznike, onda se IF–forme definiraju kao forme generirane tim skupom veznika, polazeći od neanaliziranih atoma. Npr. ako je taj skup veznika {∧, ∨, −} onda su IF–forme definirane s

(i) Atomi P, Q, R, P₁, Q₁, R₁, P₂, Q₂, R₂, … su IF–forme.
(ii) Ako je A IF–forma onda je to i (-A).
(iii) Ako su A i B IF–forme onda su to (A∧B) i (A∨B).

Na primjer, \(\small \neg \left(P_1 \vee (Q \land \neg R_2)\right)\) je IF–forma. Forme koje prethode nekoj formi u njezinoj izgradnji, ili su joj identične, zovemo podformama te forme. Dakle, podforme forme \(\small \neg \left(P_1 \vee (Q \land \neg R_2)\right)\) su \(\small P_1, \; Q, \; R_2, \; \neg R_2, \; Q \land \neg R_2\) i \(\small \left(P_1 \vee (Q \land \neg R_2)\right)\) i ona sama.

Pri pisanju IF–formi često se koristimo već uvedenim pokratama. Koristimo se i konvencijom da konkatenacija (tj. konjunkcija čiji se znak ∧ ispušta) veže jače od svih drugih znakova, te da negacija veže jače od svih drugih neispuštenih znakova. Dakle, –PQ i P ∨ QR su pokrate za (-(PQ)) i (P ∨ (Q ∧ R)), dok su –P ∧ Q i –P ∨ -Q pokrate za ((-P) ∧ Q) i ((-P) ∨ (-Q)).

Forma F je forma konkretne tvrdnje F ako se F (ili neki njen sinonim) može dobiti iz forme F interpretiranjem atoma od F odgovarajućim konkretnim tvrdnjama. U slučaju IF–formi vrijednost istinitosti koju ima interpretacija cijele forme potpuno je određena vrijednostima istinitosti koje imaju interpretacije atoma pa je zato forme dovoljno interpretirati tako da odredimo vrijednosti istinitosti njihovih atoma.

DEFINICIJA IF–INTERPRETACIJE

IF–interpretacija je pridruženje vrijednosti istinitosti ⊤ ili ⊥ atomima od kojih su izgrađene IF–forme. Pridruženje može biti totalno ili parcijalno, tj. može pridruživati vrijednosti istinitosti svim ili samo nekim atomima.

Na primjer, pridruženje vrijednosti istinitosti atomima, koje je zadano sljedećom tablicom jedna je IF–interpretacija.

­­

U toj interpretaciji forma \(\small (\overline{P} \land \overline{R}) \vee (P \land Q)\) je neistinita, tj. ima vrijednost ⊥. To dokazuje treći redak sljedeće tablice istinitosti. U njoj su izračunate vrijednosti istinitosti forme \(\small (\overline{P} \land \overline{R}) \vee (P \land Q)\) u svim (parcijalnim) interpretacijama definiranima na atomima te forme. Prva tri stupca su sve moguće (parcijalne) interpretacije atoma P, Q i R. Ima ih ukupno 8 i nalaze se u 8 redaka prva tri stupca. Daljnje vrijednosti su vrijednosti istinitosti naznačenih formi, izračunate u odgovarajućim interpretacijama. U zadnjem stupcu izračunate su vrijednosti istinitosti forme \(\small (\overline{P} \land \overline{R}) \vee (P \land Q)\) u svim mogućim interpretacijama atoma te forme.

­­

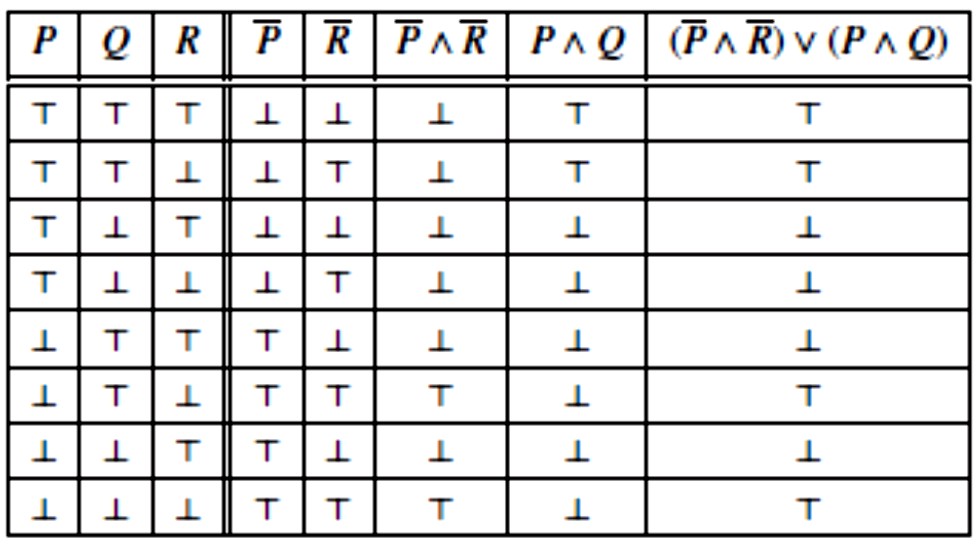
Drugi i treći korak izgradnje IF–logike sada su jednostavni.

TEOREM O TESTU VALJANOSTI

Forma A je valjana, tj. ⊡ A, ako je A istinita u svim interpretacijama. Dakle, ⊡ A testiramo tako da izgradimo tablicu istinitosti od A i provjerimo nalaze li se u stupcu ispod A sami ⊤-ovi.

TEOREM O TESTU KONZISTENTNOSTI

Forma B je konzistentna, tj. ⟐ B, ako je B istinita bar u jednoj interpretaciji. Dakle, ⟐ B testiramo tako da izgradimo tablicu istinitosti od B i provjerimo nalazi li se u stupcu ispod B bar jedan ⊤.
Na primjer, forma \(\small B = (P \land Q) \vee (P \land \overline{R}) \vee (\overline{P} \land R) \vee (\overline{Q} \land R)\) je konzistentna, jer u stupcu ispod B nalazimo ⊤-ove, ali nije valjana jer u njemu nisu samo ⊤-ovi.

­­

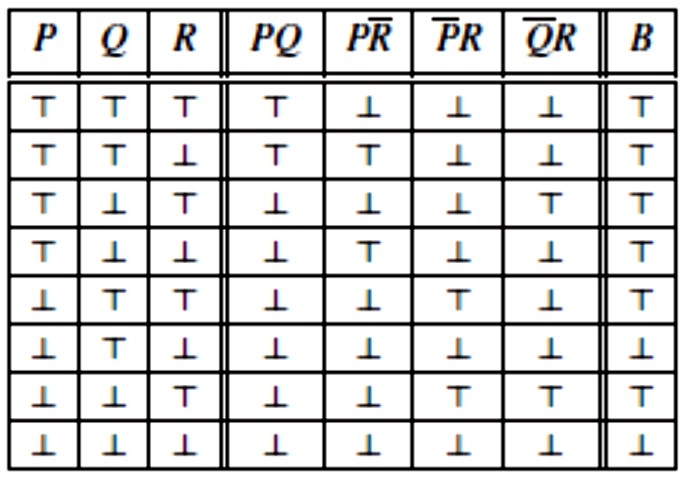
TEOREM O TESTU IMPLIKACIJE

Forme A₁,…,A_n impliciraju formu C, tj. A₁, …, A_n ⇒ C, ako ne postoji interpretacija u kojoj su sve forme A₁, …, A_n istinite, a u kojoj je C ipak neistinita. Dakle, A₁, …, A_n⇒ C testiramo tako da izgradimo zajedničku tablicu istinitosti za forme A₁, …, A_n, C i provjerimo da ne postoji redak u kojem sve forme A₁, …, A_n imaju vrijednost ⊤, a u kojem forma C ima vrijednost ⊥.

TEOREM O TESTU EKVIVALENCIJE

Forme F i G su ekvivalentne, tj. F ⇔ G, ako u svakoj interpretaciji imaju istu vrijednost istinitosti. Dakle, F ⇔ G testiramo tako da izgradimo zajedničku tablicu istinitosti za forme F i G, te provjerimo da F i G u svakom retku imaju istu vrijednost istinitosti.

Na primjer, forma \(\small F = R \vee (P \land \overline{Q})\) implicira formu \(\small G = (P \vee R)(\overline{Q} \vee R)\) jer je G = ⊤ u svakom retku u kojem je F = ⊤. One su i ekvivalentne jer zapravo u svakom retku imaju istu vrijednost istinitosti.

­­

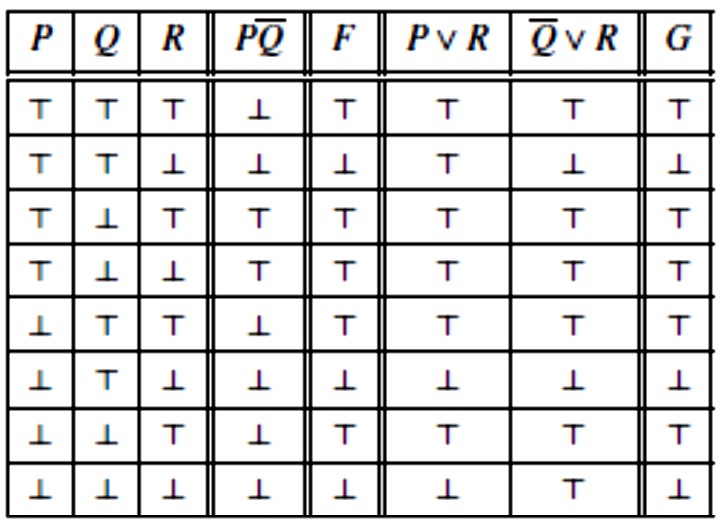
Vidimo da tablice istinitosti možemo koristiti za testiranje osnovnih logičkih relacija. Postoje i drugi testovi koji su jednostavniji i mogu se proširiti na druge logike, što nije slučaj s tabličnim testovima.