Gigerenzer vs. Kahneman. Kako ljudi stvarno razmišljaju. Koliko procjena točnosti jednog dijagnostičkog testa ima veze s vjerojatnošću?

U prethodnom članku Zvonimir Šikić nije objasnio kako je izračunao vjerojatnost da ste bolesni ako je test pozitivan. Ovisi to o pouzdanosti testa, ali i o učestalosti bolesti. Ovaj članak, u kojem objašnjava taj izračun, završava zanimljivom raspravom o prirodi 'vjerojatnosti' i ljudske racionalnosti, odnosno objašnjenjem zašto ljudi u jednom slučaju 'griješe' a u drugom ipak pogađaju kad ih pitaju - kolika je vjerojatnost da ... S jedne su strane zagovornici naivnih heuristika, a s druge evolucijski psiholozi. jedni zagovaraju fekvencijsko, drugi bayesovsko razumijevanje vjerojatnosti

Prethodni članci o matematici testiranja bolesti:

• Matematički model imuniteta stada. Dani, koeficijenti, širitelji zaraze, zaraženi, oporavljeni. Žrtve

• Kolika je vjerojatnost da ste bolesni ako je test pozitivan? Dva jednostavna pravila

Brkanje istinitosti kondicionala “ako A onda B” s istinitošću kondicionala “ako B onda A” poznata je logička greška. Manje je poznata, iako češća greška da se „vjerojatnost od B pod uvjetom da se desio A” (simbolički pr (B | A)) brka s „vjerojatnošću od A pod uvjetom da se desio B”  (simbolički pr (A | B)). Najpoznatiji je slučaj da se „vjerojatnost da ste bolesni pod uvjetom da ste pozitivni”  brka s „vjerojatnošću da ste pozitivni pod uvjetom da ste bolesni”.  Ilustrirat ću tu grešku na tom medicinskom i sljedećem sudskom primjeru:

• Prepoznavanje provalnika

U gradu u kojem se desila provala, živi 90% bijelaca i 10% crnaca. Jedina svjedokinja tvrdi da je provalnik bio crnac. Da bi se provjerila pouzdanost njezinog svjedočenja obavljena je rekonstrukcija zločina, s većim brojem bijelih i crnih “počinitelja”. Svjedokinja je u 80% slučajeva točno odredila “počiniteljevu” boju. To znači da je 80% crnih “počinitelja” prepoznala kao crnce, a 80% bijelih kao bijelce. Istražni sudac prihvatio je njezino svjedočenje kao 80% vjerojatno. Međutim, tu je gadno pogriješio.

Naime, tom je rekonstrukcijom utvrđena vjerojatnost prepoznavanja crnca, pod uvjetom da je provalnik uistinu bio crnac:

pr (P_C | C) = 80%.

Ali, sud zanima kolika je vjerojatnost da je provalnik uistinu crnac, pod uvjetom da je prepoznat kao crnac (jer to je njeno svjedočenje):

pr (C | P_C) = ?

Ta je vjerojatnost prava mjera pouzdanosti svjedočenja jedine svjedokinje i nju možemo izračunati na sljedeći način (v. donji dijagram).

Zamislimo 100 provala, bez preduvjerenja o provalnicima. Njih 90 počinit će bijelci, a tek njih 10 crnci jer je bijelaca 90% a crnaca tek 10%.

Od 90 bijelih provalnika, njih 72 (što je 80% od 90) bit će točno prepoznati kao bijelci, a njih 18 (što je 20% od 90) bit će netočno prepoznati kao crnci.

Od 10 crnih provalnika njih 8 (što je 80% od 10) bit će točno prepoznati kao crnci, a njih 2 (što je 20% od 10) bit će netočno prepoznati kao bijelci.

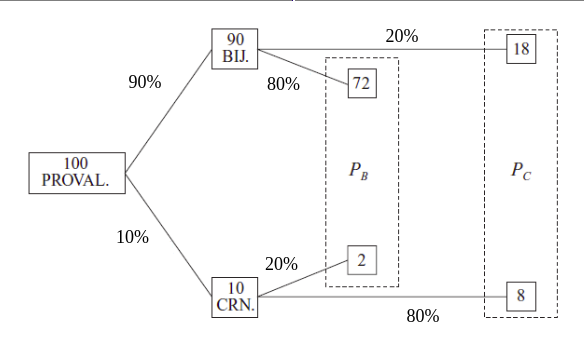
Ukupno 26 (18+8) provalnika bit će prepoznati kao crnci, a od njih će samo 8 uistinu biti crnci. Dakle, vjerojatnost da provalnik koji je prepoznat kao crnac uistinu i bude crnac iznosi 8/26 što je oko 30%:

pr (C | P_C) = 30%.

Pouzdanost svjedočenja naše svjedokinje je 30%, daleko manje od 80%.

Primijetimo još i sljedeće. Da je svjedokinja u provalniku prepoznala bijelca, to bi svjedočenje bilo mnogo pouzdanije. Naime, ukupno 74 (72+2) provalnika bit će prepoznati kao bijelci, a od njih će 72 uistinu i biti bijelci. Dakle, vjerojatnost da provalnik koji je prepoznat kao bijelac uistinu i bude bijelac iznosi 72/74 što je oko 97%:

pr (B | P_B) =  97%.

Pouzdanost svjedočenja, pr (X | P_X), ne ovisi samo o pouzdanosti svjedoka, pr (P_X | X), nego i o zastupljenosti pojedinih grupacija u populaciji, pr (X). Pogreška istražnoga suca sastojala se u tome što to nije uzeo u obzir, nego je pr (X | P_X) pobrkao sa pr (P_X | X).

• Testiranje bolesti

Želite li utvrditi da li bolujete od neke bolesti, podvrći ćete se testu. Ako je test pozitivan onda ste bolesni, a ako je negativan onda ste zdravi. Tako bar mislite vi i mnogi liječnici.

No, nijedan test nije savršeno pouzdan, pa za stvarnu procjenu vašeg stanja valja znati kolika je pouzdanost testa. Pouzdanost od 90% znači da će 90% bolesnih imati pozitivni nalaz i da će 90% zdravih imat negativni nalaz, pr (+| B) = 0.9 i pr (-| Z) = 0.9 (zbog jednostavnosti prikaza pretpostavljamo da su te vjerojatnosti jednake, što nije uvijek slučaj).

Koliko vas mora zabrinuti pozitivni nalaz, te s kolikim olakšanjem možete prihvatiti negativni nalaz ako nemate drugih indikacija da ste bolesni, osim provedenoga testa? Mnogi misle da uz pouzdanost testa od 90%, pozitivni test garantira bolest s vjerojatnošću 90%, te da negativni test garantira zdravlje s vjerojatnošću 90%. To je međutim daleko od istine.

Analogno prethodnom primjeru, zamislite 1000 testiranih ljudi (v. donji dijagram). Ako je učestalost bolesti koju testirate 1% onda je samo 10 od tih 1000 ljudi uistinu bolesno.

Od 990 zdravih, njih 891 (što je 90% od 990) negativno je, a njih 99 (što je 10% od 990) je pozitivno.

Od 10 bolesnih, njih 9 (što je 90% od 10) pozitivno je, a samo 1 (što je 10%od 10) je negativan.

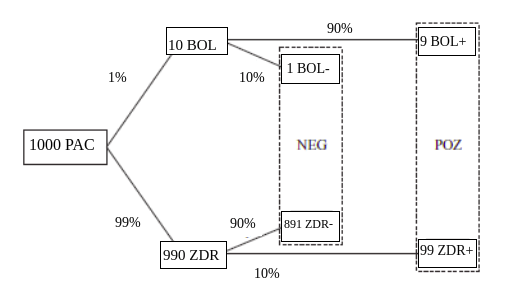
Ukupno je 108 (99+9) pozitivnih od kojih je 9 bolesno. Dakle, vjerojatnost da ste bolesni ako ste pozitivni je 9/108 što je oko 8%:

pr (B | +) = 8%

To je daleko od 90% koji su vas toliko zabrinuli.

Kao i prije, negativni test garantira vam zdravlje s vjerojatnošću mnogo bližom pouzdanosti testa (čak i većom od nje). Naime, ukupno imamo 892 (891+1) negativnih od kojih je 891 zdravo, pa vam je vjerojatnost da ste zdravi ako ste negativni 891/892 što je 99,999%:

pr (- | Z) = 99,999%.

Pogreška da se pozitivni nalaz smatra 90% garancijom bolesti još je jednom pogreška brkanja pr (+| B) = 90%  sa pr (B | +) = 8%.

• Bayesova formula

Sve se to može izraziti i matematičkom formulom koja povezuje relevantne vjerojatnosti. Naime, na gornjem dijagramu matematički utrenirani čitatelj može pratiti kako smo izračunali pr (B | +):

pr (B | +) = pr (B +) / pr (+) = pr (B) pr (+ | B)) / pr (+)

To je slavna Bayesova formula koja pokazuje kako se pr (B | +) može izračunati iz pr (B), pr (+) i pr (+ | B). U tom kontekstu vjerojatnost pr (B | +) zove se posterior jer se radi o procijenjenoj vjerojatnosti da je netko bolestan nakon što znamo da je pozitivan, tj. radi se o procjeni a posteriori. Vjerojatnost pr (B) se zove prior jer se radi o procijenjenoj vjerojatnosti da je netko bolestan prije nego što znamo da je pozitivan, tj. radi se o procjeni a priori. Vjerojatnost pr (+ | B) zove se pouzdanost. Dakle, Bayesovom formulom iz apriorne vjerojatnosti i pouzdanosti računamo aposteriornu vjerojatnost.

Mada se radi o istom sadržaju u različitom pakiranju, ljudi najčešće ne razumije Bayesovu formulu i zbunjuje ih sva ta terminologija, iako razumiju prethodno (inače matematički ekvivalentno) rasuđivanje pomoću frekvencija i njima odgovarajućih dijagrama. To ukazuje na važnost načina na koji prezentiramo neki sadržaj.

• Evolucijska psihologija i naivne heuristike

No, to nije samo pedagoško pitanje nego je jedan od važnih razloga razmimoilaženja između Kahnemana, Tverskog i drugih zastupnika teze naivnih heuristika s Gigerenzerom i drugim evolucijskim psiholozima oko razumijevanja ljudske racionalnosti.

Prosudbe vjerojatnosti podložne su naivnim heuristikama. Daniel Kahneman (youtube).

Vidjeli smo da vjerojatnost neke hipoteze dijelom ovisi i o apriornoj vjerojatnosti te hipoteze. Međutim, u nizu slavnih eksperimenata Kahneman i Tversky pokazali su da ispitanici ozbiljno podcjenjuju važnost tih apriornih vjerojatnosti. Na primjer, jednoj grupi ispitanika dali bi da među 100 kratkih prikaza osoba, od kojih je 30 inženjera i 70 pravnika, slučajno odaberu 5 prikaza te da za svaki procijene vjerojatnost prikazuje li inženjera ili pravnika. Druga grupa ispitanika dobila je prikaze 70 inženjera i 30 pravnika. Prikazi su bili tri vrste: stereotipni prikaz inženjera, stereotipni prikaz pravnika ili potpuno neutralni prikaz. Na primjer:

Ivan pokazuje zanimanje za politička i društvena pitanja i većinu svog slobodnog vremena provodi čitajući novine i publicistiku.

Marko je 30-godišnji muškarac, oženjen i bez djece. Čovjek je visokih sposobnosti i obećava da će biti prilično uspješan u svom području.

Kao što se i očekivalo, ispitanici u obje skupine ocijenili su vjerojatnost da je Ivan pravnik prilično velikom. U potpunom nesuglasju s Bayesovom formulom, razlika u odgovorima dviju skupina gotovo da nije postojala. Zanemarivanje podataka o apriornoj vjerojatnosti (base-rate), 30-70 odnosno 70-30, još je upečatljivija u slučaju Marka. Njegov je opis konstruiran kao potpuno neinformativan u pogledu njegove profesije. Stoga su jedine korisne informacije koje su ispitanici imali bile one o 30-70 odnosno 70-30 raspodjeli inženjera i pravnika. Ali oni su te informacije potpuno zanemarili pa je srednja procjena vjerojatnosti u obje skupine bila 50%.

Ovakvi problemi obično nemaju veliki praktični značaj, ali postoje neke značajne iznimke poput ranije razmatranog testiranja bolesti. U uznemirujućoj studiji iz 1978.  Casscells je opisao sljedeći problem koji je postavio grupi profesora i studenata četvrte godine na Harvard Medical School:

Učestalost bolesti je 0.1%, a test za njeno otkrivanje daje 5% lažno pozitivnih rezultata. Kolika je šansa da osoba koja ima pozitivan rezultat bude bolesna (pod pretpostavkom da ništa ne znate o simptomima ili drugim indicijama bolesti u te osobe)?

Točan odgovor je 2%. Ali samo 17% profesora i studenata s Harvarda odgovorilo je iole blizu 2%. Njih čak 45% potpuno je ignoriralo informaciju o učestalosti bolesti (apriorni base rate) i odlučilo se za 95%.

Ovi i mnogi slični rezultati naveli su  Kahnemana, Tverskog  i mnoge druge na zaključak da ljudi kada prosuđuju vjerojatnosti redovito odstupaju od standardnih normi racionalnosti i koriste se naivnim heuristikama. To je osnovna teza programa naivnih heuristika (heuristics and biases program). Riječima Kahnemana i Tverskog iz 1974:

Pri predviđanju i prosudbi neizvjesnih događaja, čini se da ljudi ne slijede račun vjerojatnosti ili statističku teoriju predviđanja. Umjesto toga, oni se oslanjaju na ograničeni broj heuristika koje ponekad donose razumne prosudbe, a ponekad dovode do ozbiljnih i sustavnih pogrešaka.

Ili još ekstremnijim riječima Piattelli-Palmarinija iz 1994:

Vjerojatnostna intuicija svakoga tko nije naučio račun vjerojatnosti ima vjerojatnost veću od 50% da bude kriva.

Kahneman i Tversky će do 1983. donekle ublažiti svoj stav dopuštajući da naivne heuristike ne sprečavaju uporabu drugih postupaka. Do 1988. prihvatit će umjereniju hipotezu da su vjerojatnostne prosudbe tek vrlo osjetljive na naivne heuristike.

Donekle različit pogled imaju evolucijski psiholozi. Oni ljudski um vide kao veliki broj sustava posebne namjene , tzv. „modula“ ili „mentalnih organa“ koji su specijalizirani za pojedina područja i urođeni su svim normalnim pripadnicima vrste. Suprotno onome što su tvrdili Jerry Fodor i drugi, ta modularna struktura uma nije ograničena samo na sustave odgovorne za percepciju, obradu jezika i motoričke akcije, nego postoje i moduli odgovorni za rasuđivanje. Naravno, za evolucijske psihologe ti su mentalni moduli evolucijske prilagodbe. Kako su 1995. argumentirali Tooby i Cosmides:

Naša kognitivna arhitektura nalikuje konfederaciji stotina ili tisuća funkcionalno namjenskih računala (često nazivanih modulima) dizajniranih za rješavanje adaptivnih problema naših lovačko-sakupljačkih predaka. Svaki od ovih uređaja ima svoj program i nameće svoju specifičnu organizaciju različitim dijelovima svijeta. Postoje specijalizirani sustavi za generiranje gramatike, za prepoznavanje lica, konstrukciju predmeta, čitanje emocija s lica … prepoznavanje smjera pogleda, detekciju varanja … “teoriju uma” …. i mnoštvo drugih elegantnih strojeva.

Ako je veliki dio kognicije zaista potkrijepljen kognitivnim modulima koji su dizajnirani da bi se bavili adaptivnim problemima koje je nametao svijet u kojem su živjeli naši preci, onda bismo trebali očekivati ​​da će moduli odgovorni za rasuđivanje biti najuspješniji ako informacije dobivaju u formatu u kojem su one bile dostupne tim našim precima. Njima je (kao što je Gigerenzer argumentirao 1994.) bilo dostupno mnoštvo korisnih probabilističkih informacija, ali predstavljenih u obliku “frekvencija događaja, kodiranih onako kako  su doživljeni – na primjer kao 3 od 20, a ne kao 15% ili 0,15.”

U suprotnosti s originalnim eksperimentom, u kojem je samo 17% ispitanika dalo (bar približno) točan odgovor, na frekvencijski formulirani problem točan je odgovor dalo 76% ispitanika.

Cosmides i Tooby argumentiraju na isti način:

Naši hominidski preci bili su uronjeni u bogati tijek uočenih frekvencija koje su mogli koristiti za bolje odluke … Dakle, ako imamo prilagodbe za induktivno zaključivanje, one bi trebale koristiti informacije u obliku frekvencija.

Na temelju takvih evolucijskih razmatranja, Gigerenzer, Cosmides i Tooby predložili su i branili psihološku hipotezu koju nazivaju frekvencijskom hipotezom:

Neki naši mehanizmi induktivnog zaključivanja utjelovljuju aspekte računa vjerojatnosti, ali su osmišljeni tako da na ulazu primaju informacije o frekvencijama i kao izlaz također proizvode frekvencije.

Ove spekulacije navele su Cosmides i Tooby da provedu seriju eksperimenata u kojima su Casscellsov “problem medicinske škole na Harvardu” sustavno transformirali u problem u kojem su i ulazna informacija i odgovor formulirani kao frekvencije (dakle onako kako smo ih gore prezentirali u primjerima provalnika i testiranja bolesti):

1 od 1000 Amerikanaca ima bolest X. Test za otkrivanje te bolesti na svakih 1000 rezultata daje 50 lažno pozitivnih rezultata. Zamislite da je lutrijom odabrano 1000 Amerikanaca koji su zatim testirani (organizatori lutrije nisu imali nikakve informacije o zdravstvenom stanju nikoga od tih ljudi). S obzirom na navedene podatke, koliko će (u prosjeku) pozitivnih ljudi zaista biti bolesno?  Odgovor: _____ od _____.

U suprotnosti s originalnim eksperimentom, u kojem je samo 17% ispitanika dalo (bar približno) točan odgovor, na frekvencijski formulirani problem točan je odgovor dalo 76% ispitanika. To nije izolirani slučaj.  Pokazalo se da u mnogim slučajevima, kada su problemi postavljeni u frekvencijskom obliku, ispitanici rasuđuju na korektan način. Iako je sporno kako točno objasniti tu činjenicu, prihvaćaju je i evolucijski psiholozi i zagovornici naivnih heuristika.

Vjerojatnosti mogu imati isključivo frekvencijsku interpretaciju.Greg Gigerenzer (youtube)

Iako je još uvijek tema znanstvene polemike što ti rezultati dokazuju o prirodi i dosegu ljudske racionalnosti, čini se da evolucijski psiholozi smatraju da um sadrži jedan ili više frekvencijskih modula koji su prirodnim odabirom ustrojeni da stvaraju normativno korektne prosudbe, kada im se pruže odgovarajući frekvencijski inputi. S druge strane, sljedbenici programa naivnih heuristika, iako to ne dovode u pitanje, smatraju da se ljudi koriste i naivnim heuristikama koje ih, kada prosuđuju vjerojatnosti, često odmiču od tih korektnih normi racionalnosti. Tu zapravo i nema sukoba.

Stvarni je sukob oko interpretacije pojma vjerojatnosti. Gigerenzer drži da vjerojatnosti mogu imati isključivo frekvencijsku interpretaciju (prema kojoj se vjerojatnosti tumače kao relativne frekvencije događaja) pa zato uopće nema smisla govoriti o ​​vjerojatnostima pojedinačnih događaja. Gigerenzer će zato tvrditi da „zakoni vjerojatnosti govore o frekvencijama, a ne o pojedinačnim događajima“, i stoga će inzistirati da „nijedan sud o pojedinačnom događajima ne može biti pogrešan sa stajališta teorije vjerojatnosti“. Kahneman, Tversky i njihovi sljedbenici inzistiraju na tome da se teorija vjerojatnosti može smisleno primijeniti na pojedinačne događaje, pa stoga i na procijene vjerojatnosti pojedinačnih događaja (npr. na procjenu vjerojatnosti da je Ivan pravnik) .

Gigerenzerov je pristup izuzetno restriktivan i ne može objasniti mnoge uspješne primjene vjerojatnosti, od svakodnevnog života do prirodnih znanosti. Izvan ovoga konteksta poznat je kao sukob frekvencijskog i bayesovskog razumijevanja vjerojatnosti. O tome više u https://www.ffri.hr/phil/casopis/content/volume_10/10_1_2.pdf.