Kako su nastali brojevi, računanjem ili apstrahiranjem

U drugom članku o radu francuske matematičarke i povjesničarke Karine Chemla fokus je na njezinom istraživanju o razvoju brojeva i decimalnog sustava s mjesnom vrijednošću broja u Kini. Prema Željku Ivankoviću istraživanje povijesti i matematičke prakse u različitim kulturama potkrepljuje zaključak o praktičnoj prirodi matematike

• Naslovna fotografija: Decimalni sustav brojeva na kineskom, pronađen u rukopisima iz Dunhuanga s kraja 10. stoljeća (Gresham College)

I

U prethodnom članku o radu francuske matematičarke, povjesničarke i filozofkinje Karine Chemla prikazana je njezina usporedba matematičkog dokaza u zapadnoj i kineskoj tradiciji. U članku se ističe  (a) da su matematičke prakse vidljivo različite u različitim kulturama i ‘civilizacijama’ i (b) da se matematika kroz povijest razvijala. Oboje se uglavnom smatra akcidentalnim, kako za prirodu matematike tako i za matematičko obrazovanje. Karine Chemla, međutim, oboje smatra bitnim: iz povijesnih i istraživanja razlika matematičkih kultura nastoji izvesti zaključke o prirodi matematike. U ovom se članku prikazuje njezino istraživanje o nastanku brojeva u davnim kulturama Istoka. Chemla neskriveno sugerira da bi isti opći zaključci bili izvedeni i kad bi se njezine hipoteze primijenile na u istraživanju matematike na Zapadu. Ustvari radi se o razumnom očekivanju da se priroda brojeva otkriva u sličnosti u različitim kulturama. Zato istraživanje povijesti i različitih kultura može biti plodonosno.

Zaista, ako je matematika uvijek ista za sve, a matematičke istine vječne i neupitne, zašto postoje različite matematičke kulture i zašto se matematika uopće razvijala? Najbanalnije pitanje glasi: ako je 2 + 2 = 4, i ako je to očito, zašto neki to ipak ne vide odmah nego to spoznaju (ili prihvate) tek računanjem na prste ili s hrpicama kamenčića? Ili povlačeći crte u pijesku ili prašini? Zašto se ono što je očito i neupitno ipak mora spoznavati? I zašto nije odmah prezentno, od početka do kraja? Kad se, na primjer, ipak usvoji kao neupitno da je 2 + 2 = 4, zašto nije odmah očito i da je 7 + 5 = 12 nego se mora izračunavati (iako je u osnovi isto kao 2 + 2 = 4)? Slijedi i novo pitanje: ima li nešto u tome što se matematičke istine u različitim sredinama spoznaju različitim putevima? S time je povezano i pitanje zašto se u različitim sredinama matematika poučava različitim redoslijedima?

Ovdje se, da ne bi bilo zabune, ne dovodi u pitanje da je 2 + 2 = 4, uvijek i svugdje, niti se raspravlja metafizički status te ‘istine’ nego se postavlja pitanje spoznavanja te istinite tvrdnje i razlika u putevima dolaženja do matematičkih ‘istina’[i].  Pri tome se stvar ne promatra iz psihološkog kuta niti se raspravlja o mentalnim kapacitetima za matematičku spoznaju nego je tema: može li se iz povijesti matematike i razlika matematičkih kultura naučiti o prirodi matematike više nego što se uglavnom pretpostavlja.[ii]  Što je, uostalom, početak matematike?

Francuska matematičarka Chemla i dva Springerova zbornika iz povijesti matematike koja je uredila.

II

Broj, brojevi, svakako kandidiraju za ‘ono što je bilo na početku’. Prema matematičaru Leopoldu Kroneckeru ‘prirodne brojeve stvorio je bog; čovjek je napravio ostalo’. Prošli članak usporedio je euklidski aksiomatski, geometrijski dokaz s dokazom ispravnosti procedure kalkulacije (algoritma) u Kini. I ovaj je put korisno krenuti od Euklida.

Sedma knjiga Elemenata bavi se brojevima. Počinje apstraktnim definicijama. Prema definiciji 2. ‘broj je mnoštvo onoga što je sastavljeno od jedinica’. Iz te definicije slijedi da ‘jedinica’ – nije broj: jedinica nije mnoštvo. U prvoj je pak definiciji ‘jedinica’ definirana kao ono po čemu se svaka stvar naziva ‘jedan/jedno’ (ono što je jedinstveno, pojedinačno). Prve dvije definicije snažno sugeriraju ono što je česta interpretacija grčkog shvaćanja brojeva da ‘1’ (jedan) dakle nije broj. Danas se tako uglavnom ne misli – jedan je broj, kao uostalom i nula. Zapravo, jedan je broj zato što je i nula broj. Odnosno, kad je nula usvojena kao broj, a znamo da to u zapadnoj matematici nije bilo otpočetka, i jedan je mogao postati broj. Slijedi Euklidova definicija 3, prema kojoj je ‘broj dio broja, manje od većeg, kad mjeri to veće’ (kurziv je moj). I ostale definicije više izazivaju pitanja nego što daju odgovora. Formulirane su tako da su i danas predmet filoloških i filozofskih tumačenja. Na primjer ‘broj je veći kad je mjeren manjim umnožak manjeg’. Koliko god nam danas formulacija bila nespretna sugerira da je u euklidskoj tradiciji usporedivost karakteristika brojeva: neki su veći, drugi manji[iii]. Indikativno je da se umnožak dva broja naziva ploha, čije su stranice ti brojevi (def. 16), a tri pomnožena broja su tijelo (def. 17), što jasno ilustrira poznati zaključak da su Grci o brojevima mislili geometrijski[iv].

U sedmoj knjizi Elemenata Euklid je pokušao definirati brojeve.

Ova se apstraktna razmišljanja mogu činiti produktivnima ili neproduktivnima[v], no u filozofiji su se i matematici slične rasprave nastavile do danas. Chemla se odlučila u istraživanju istih pitanja krenuti drugim, zaobilaznim putem. U zborniku Cultures of Computation and Quantification in the Ancient World (Springer, 2022), kojem je jedna od urednica, umjesto u apstraktnim euklidskim raspravama, porijeklo i prirodu brojeva traži u kulturama Mesopotamije, Indije i posebno Kine.

III

Prvi je i glavni zaključak francuske matematičarke da su brojevi nastali kao ishod matematičkih operacija. Na prvi se pogled ne čini sumnjivim. Ipak, iskrsava pitanje moguće cirkularnosti: zar nisu brojevi pretpostavka matematičkih operacija, zar nisu za zbrajanje prethodno potrebni brojevi. Mogući je odgovor da brojevi ne nastaju iz zbrajanja nego iz brojanja. No, postoji i kontratvrdnja – da je i brojanje vrsta zbrajanja, iako je zacijelo plodno diskutirati i o njihovim (mogućim) razlikama.

Uvodni članak, koji zauzima 130 gusto pisanih stranica, Chemla započinje navođenjem dviju knjiga. Prva je Universal History of Numbers. From Prehistory to the Invention of the Computer (Georges Ifrah, New York, Willey, 2000), a druga A Brief History of Numbers (Leo Corry, Oxford University Press, 2015). Obje su dakle o povijesti brojeva, no njihov je sadržaj različit, pišu o različitim stvarima. Chemla pojednostavljuje: Ifrahova knjiga pažnju dominantno posvećuje povijesti zapisivanja brojeva i računanja s njima, a druga, Corryjeva, bavi se poviješću ideje (pojma) broja.

Obje su knjige o povijesti brojeva, no sadržaj je različit: Lijeva se fokusira na povijest zapisivanja brojeva, a  desna se bavi poviješću ideje broja.

O čemu se radi kad se istražuje povijest ideje broja, odnosno pojam. Već je spomenuto da u nekim davnim koncepcijama 1 (jedan) nije broj, a o nuli kao broju se i ne razmišlja. S vremenom u brojeve su ipak uključivani i negativni (koje Euklidova definicija očito ne obuhvaća), zatim razlomci, racionalni, realni, kompleksni brojevi. Tijekom povijesti se odgovor na pitanje što je broj, odnosno – pojam/ideja broja, očito širio. Kad se pak istražuje notifikacija (zapisivanje) brojeva, misli se na to kako su brojeve bilježili Rimljani, Grci, Kinezi, Arapi, čiji je način preuzeo i Zapad, i kako se računalo u pojedinim sustavima notifikacije. U povijesti notifikacije posebno je važan koncept mjesne vrijednosti broja uz što su vezani decimalni, heksadecimalni, pa na koncu i binarni brojevni sustav.

Druga je teza Karine Chemla da se te dvije povijesti ne mogu odvajati. Ustvari, čita li se pažljivije, ona razvitak pojma broja rekonstruira iz načina bilježenja brojeva. Zaista, mjesna vrijednost broja nije samo metoda bilježenja, nego je isprepletena s matematičkim operacijama množenja i potenciranja. Mjesna vrijednost otkriva dakle nešto i o prirodi brojeva. Same matematičke operacije koje omogućavaju proširivanje pojma broja na negativne, racionalne itd. ovise, odnosno u uskoj su vezi s načinom bilježenja brojeva.

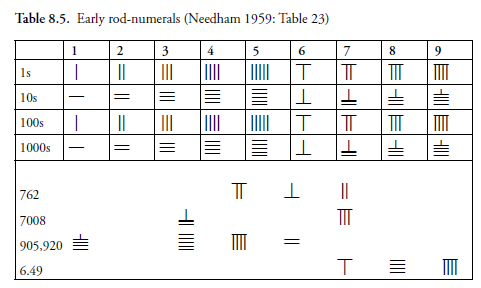
Dokumenti iz kojih se vidi način bilježenja brojeva i računanja najvažniji su, ali ne i jedini izvor Karine Chemla. Neizbježno u obzir uzima i oruđa za računanje, štapiće (counting rods), kamenčiće, ploče odnosno površine na kojima su se matematičke operacije izvodile. Jedan od načina bilježenja brojeva u Kini su numeral–rods, crtice vrlo slične nekim pretpostavljenim bambusovim štapićima koji su se premiještali na površini za računanje kad su izvođene matematičke operacije. Sustav bilježenja brojeva pomoću tih crtica (numeral–rods) vrlo je sličan abacusu, koji se pak služi kuglicama, i na kojem su se u Kini praktički ‘do jučer’ izvodile vrlo složene matematičke operacije, čak potenciranje na treću (a vjerojatno se ponegdje izvode i danas).

Kad se na nekom mjestu u broju pojavi nula to se mjesto jednostavno preskoči: rani brojevni štapići ovdje preslikani iz knjige Numerical Notations Stephena Chrisomalisa (vidi bilješku vii).

Treća je teza Karine Chemla da broj nije puki lingvistički entitet, odnosno da zapisivanje brojeva nije lingvistička operacija. Lingvističko porijeklo znamenke, koje je vrlo rašireno u literaturi, Chemla mora opovrgnuti, ustvari ograničiti, upravo da bi otvorila put svojem shvaćanju bilježenja brojeva i kreiranja pojma broja kao ishoda matematičke operacije. Zapisivanje broja 2 slovima, znamenkom, rimskom ili arapskom notacijom, nije tek bilježenje onog što je naglas ili u sebi izgovoreno. Ponekad naravno jest. Rimljani su broj 100 pisali slovom C, od latinske riječi centum, koja znači stotinu. Neki su zapisi brojeva u davnim spisima nesumnjivo morfemi, s druge strane znamenka je simbol koji kao isti broj čitaju govornici različitih jezika. Chemla se prilično muči da limitira vezu jezika i broja. Na slične teškoće razgraničenja svojeg razumijevanja porijekla i prirode broja Chemla nailazi kad ga pokušava odvojiti od još jedne česte predodžbe, da je broj apstrakcija različitih veličina, recimo tri kruške, tri jabuke kojima je zajedničko – 3.

Četvrta je njezina teza da broj nije ishod apstrakcije onog što je zajedničko u mjerenju veličina na temelju mjernog standarda. Treba biti pažljiv: iz shvaćanja porijekla broja (a time i pojma broja) Chemla ne isključuje mjerenje, naprotiv. Mjerenje je inicijalno usporedba većeg i manjeg; odgovorom na pitanja za koliko? i koliko veće?, a uz pretpostavku mjerne jedinice, razvija se u brojanje. Chemla međutim razlikuje kvantifikaciju i numeraciju. Može se zaključiti da je broj kao apstrakcija kolikoće iz kakvoće shvaćen na jedan način, a kao ishod računanja na drugi način. U nekom smislu apstrahiranje kolikoće od kakvoće nije matematička operacija, nego je formiranje broja apstrahiranjem pretpostavka matematičkih operacija.

To je, međutim, suprotno tezi Karine Chemla da ono što se dobije apstrahiranjem postaje brojem tek kao sastavnica ili ishod matematičke operacije. Stoga ona i tezu o nastanku broja apstrahiranjem relativizira. Tezom o kreiranju (pojma) broja u matematičkoj operaciji ujedno, dakle, na svoj način definira pojam broja. Drugim riječima, može joj se prigovoriti da definiciju broja i razliku kvantifikacija: numeracija prilagođava svojoj tezi o porijeklu broja iz matematičke operacije.

U nastavku je video-snimka predavanja koje je Chemla održala na Gresham College, u kojem se spominju sve ove glavne teze, a broj koji identificira kao ishod (i pretpostavku?) matematičke operacije naziva – čistim brojem.

U predavanju koje je održala na Gresham College Karine Chemla je formulirala ovdje spomenute glavne teze iz Uvoda u zbornik.

IV

Prethodne distinkcije i teze Karine Chemla postaju jasnije tek u njezinu materijalnom istraživanju. Primjer kojim se detaljno bavi su – cigle. Cigle se može brojati, može im se mjeriti volumen (ako ih se prevozi na nekoj vrsti kola), može im se mjeriti i težina, koja ovisi o tome jesu li suhe ili vlažne. Za broj cigli, volumen i težinu postoji neki standard. Standard  na temelju kojeg bi se mjerio učinak radnika koji prevozi cigle ustvari se ne može ustanoviti unaprijed, nego naknadno, nakon rada neko vrijeme i nekoliko radnika, na temelju nekog prosjeka, a ovisi o težini cigli, volumenu, veličini kola itd. Standard se uspostavlja radi plaćanja nadnice, a uspostavlja se najjednostavnijim matematičkim operacijama i to zato što se u administraciji gradnje nastoji izbjeći arbitrarnost[vi].

Pronađene su tablice u kojima su i nadnice za prijevoz određenih količina cigli, bilo da je riječ o broju ili volumenu (kolima). Uz te tablice, na margini, ali očito kao obavezan element, upisani su koeficijenti na temelju kojih se iz količina izračunava plaća. Te koeficijente Chemla proglašava brojem kao takvim (odnosno – kako u gornjem videu kaže: ‘pure number’). Koeficijenti ne označavaju količinu. Oni nisu ni apstrakcija iz količina (tri jabuke, tri kruške, tri cigle, troja kola, tri dana). Oni su jednostavno – broj. U isti su mah ishod i sastavni dio matematičke operacije. Oni su samostojeći. Imaju svoj autonoman zapis iz kojeg je jasno da su broj a ne količina nečega niti zapis neke izgovorene riječi.

Ilustracija iz zbornika kojom Karine Chemla objašnjava da su koeficijenti zapisivani posebno, kao samostalni brojevi, i svojim znakovnim sustavom, različitim od onog koji se koristio za mjere i mjerne jedinice

U gornjem videu, nakon 28 minute Chemla objašnjava različitu poziciju broja kao mjere i broja kao koeficijenta.

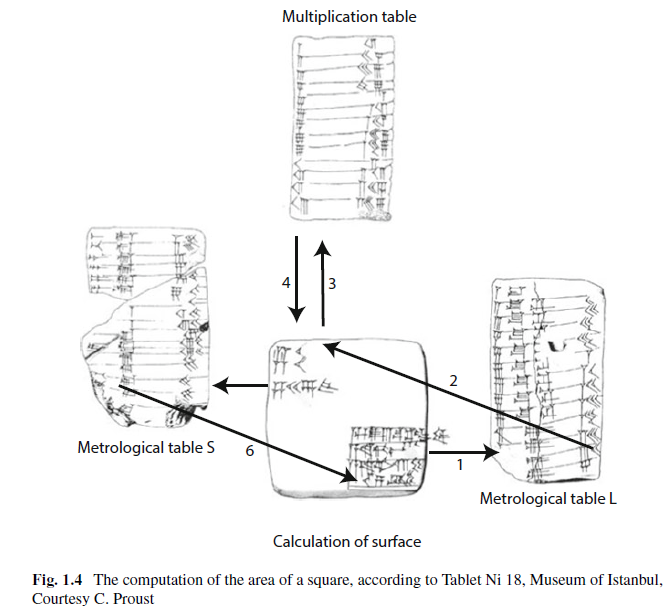
Chemla ustanovljuje i dokazuje da se količine zapisuju drukčije, a da koeficijent, broj, čija je jedina svrha matematička operacija ima svoju samostalnu notifikaciju. Količina se na primjer može izraziti kolima, tačkama, lopatom, naramkom. Koeficijent je koeficijent. On postoji samo u matematičkoj operaciji, zbog koje i iz koje nastaje. Priroda koeficijenta nije u nekoj apstrakciji iz količina nego u upotrebi u matematičkoj operaciji. Koeficijent je ništa drugo nego broj. Ispada da za Chemlu kultura kvantifikacije još-nije-matematika, a kultura numeracije je matematika. Tvrdi da je ta razlika identifikabilna u formi zapisa, odnosno da je upravo forma zapisa razotkriva.

V

Kad je pak riječ o mjesnoj vrijednosti znamenke, kao sastavnice decimalnog sustava, stvar je u osnovi ista: i tu su, prema Chemli, glavnu ulogu imale matematičke operacije, odnosno ‘računanje’, kako na jednom mjestu eksplicira pojam matematičke operacije. Sve je ipak znatno kompliciranije. Chemla naznaku decimalnog sustava u Kini smješta u prvo stoljeće nove ere. Neki istraživači mjesnu vrijednost broja a i adekvatni sustav pronalaze čak 1500 godina prije[vii]. Radi se o zapisima koji prikazuju bambusove štapiće kojima se brojalo ali tako da su jedan, dva, tri …. uspravna bambusova štapića označavala neki broj, a horizontalni je štapić označavao broj pet.

Kineski abacus ima i takvo brojanje i decimalni sustav: na jednom se dijelu prve osovine pomiču kuglice do pet, kad se dostigne to se zabilježi prelaskom na drugi dio te osovine, nastavi se do devet, a zatim se ide na sljedeću osovinu. Znalac na abacusu može izvoditi složene matematičke operacije. Praktički do jučer se koristio na tržnicama, u dućanima, i u knjigovodstvu u poduzećima, a zacijelo se ponegdje još koristi. Oni koji decimalni sustav s mjesnom vrijednošću broja pronalaze čak 15 stoljeća p.n.e, pretpostavljaju iz činjenice da se bambusovim štapićima brojalo po istom sustavu kao na abacusu da je postojala i računalna ploča na kojoj su se izvodile operacije kao na abacusu.

Brojanje na abacusu.

Množenje abacusom.

Chemla se ne slaže s takvim načinom zaključivanja. Riječ je o projekciji abacusa, kasnijeg sustava, u prethodni, a sve na temelju jedne sličnosti: brojanja. Takvim se zaključivanjem zanemaruje nedostatak dokumenata odnosno materijalnih dokaza a ujedno se negira i razvoj. Chemla polazi od pretpostavke da matematika ima povijest. U računalnim štapićima u kojima ih se brojanjem grupira u pet, deset, pedeset, može biti neki zametak decimalnog sustava, ali to – prema Karine Chemla – nije decimalni sustav. I u razlici zapisivanja rimskih brojeva IX i XI, kad se jedinica stavlja ispred ili iza desetke ima nešto od mjesne vrijednosti broja. Ali to nije ista mjesna vrijednost znamenke kao u broju 237.

Za potvrdu postojanja decimalnog sustava važne su dvije operacije – množenje i dijeljenje. Chemla analizira izvore u kojima se paralelno izvode operacije koje se služe i one koje se ne služe decimalnim sustavom. Radi se, recimo, o množenju višeznamenkastih brojeva. U istom se dokumentu mogu naći primjeri izračunavanja umnoška ‘pješice’ i prema pravilima množenja višeznamenkastih brojeva u decimalnom sustavu s mjesnom vrijednošću broja. U izračunavanju ‘pješice’ stotice, desetice itd iz množenika se razdvoje, svaka se pojedinačno zbroji onoliko puta koliki je množitelj i onda sve još jednom zbroje u umnožak. U drugom slučaju postoje pravila potpisivanja međukoraka množenja jedinicama, deseticama, stoticama itd. Ovisno o tome koji je način množenja primijenjen u istom se dokumentu množenje zapisuje različitim notifikacijama. Kad se računa ‘pješice’ zapisuje se znakovima kojima se bilježe količine, u drugom slučaju se postupak bilježi znakovima kojima se bilježe brojevi. U jednom je riječ o kvantifikaciji u drugom o numeraciji. To je jedan od najjačih argumenata Karine Chemla o povezanosti načina bilježenja brojeva i matematičkih operacija.

Važno je to što se u istom izvoru pojavljuju dva načina izračuna. Jedan način izvedbe matematičkih operacija koristio se u administraciji, recimo radi poreza ili obračuna nadnice, koji su se izračunavali na temelju mjernih tablica s količinama, drugi u obrazovanju matematičara. Sustav ‘korak po korak’ je transparentniji, drugi efikasniji. Zato se i stoljećima kasnije mogu istodobno u upotrebi naći ‘razvijeni’ i ‘nerazvijeni’ sustavi koji se koriste i različitim načinima zapisivanja brojeva.

U knjizi Numerical Notations Chrisomalis pisanje broja 2340 u Kini na način 2×1000+3×100+4×10 naziva multiplikativno-aditivnim decimalnim sustavom, ali u kojem je mjesna vrijednost znamenke tek možda u začetku.

Prema Chemla, sustav u kojem se umnožak izračunava ‘korak po korak’ nije decimalni sustav s mjesnom vrijednošću broja u punom smislu riječi. Chrisomalis i drugi sustav klasificira kao decimalni, budući da mu je baza deset, ali ga naziva multiplikativno-aditivnim, a još ne sustavom s mjesnom vrijednošću broja. U njemu se broj 2340 piše kao 2×1000+3×100+4×10, ali se mogao pisati i kao 3×100+4×10+2×1000, dakle stotice + desetice + tisuće. To je vrlo dobra ilustracija da se decimalni sustav s mjesnom vrijednošću broja razvijao, da se nije pojavio odjednom, kompletan, kao kakva genijalna inovacija.

Pri kraju Uvoda (str. 131) Chemla iznosi tezu da je i matematički dokaz povezan s matematičkim operacijama. Izgleda očito, ali kako su, prema osnovnom zaključku njezina istraživanja operacije isprepletene s brojevnim i sustavom bilježenja brojeva slijedi da se neke matematičke tvrdnje u jednom sustavu mogu dokazati, u drugom ne mogu. Matematički dokazi dokazuju nešto vječno, što vrijedi svuda, a ispada da ovise o ‘alatima’ kojima se izvode. Po običaju Chemla zaključuje – tu je potrebno daljnje istraživanje, posebno matematičkog simbolizma, no i to sugerira da su razvoj (odnosno povijest) matematike a i njezina priroda isprepleteni s načinom bilježenja brojeva.

VI

U istraživanjima i zaključcima Karine Chemla lako se izgubiti. U sljedećim primjerima njezine se teze pokušavaju primijeniti i na slučajeve koje sama ne spominje a nama su poznati. Radi se o pokušaju univerzalizacije kao obliku provjere razumijevanja njezinih zaključaka. Ako sam je dobro razumio, tezu o razotkrivanju pojma broja u notaciji ilustrira i razmjerno suvremen i donekle radikalan primjer kompleksnih brojeva. Korijen iz minus jedan proširuje pojam broja, a istovremeno uvodi i novu notaciju. Lako je moguće da će se za koju tisuću godina puni razvoj i korištenje imaginarnih brojeva rekonstruirati iz notacije, kao što Chemla iz matematičkih operacija koje se izvode u određenom sustavu pisanja brojeva identificira nastanak ‘broja kao takvog’ (pure number).

U sljedećem videu ukratko se opisuje razvoj matematičkih operacija do invencije imaginarnog broja te mijenjanje i razvoj notacije.

Chemla (kao i neki drugi istraživači), dijeljenje identificira kao ‘najproduktivniju’ matematičku operaciju u razvoju pojma broja i adekvatnih brojevnih sustava. Dijeliti se može ‘s ostatkom’, mogu se pisati razlomci, a mogu se iza zareza bilježiti i decimale. Dijeljenje ‘proizvodi’, racionalni i realni broj. Korijen je klasificiran kao oblik dijeljenja.

U prethodnom smo članku citirali Johna Stillwella[viii] prema kojem se grčka matematika odvojila od istočne kad je uočivši iracionalnost korijena iz dva krenula putem strogog (euklidskog) dokaza. Azija je poznavala iracionalnost korijena iz dva ali kao da u tome nije vidjela problem koji bi je izazvao razvijati aksiomatski euklidski tip dokaza. Korijen iz dva je – korijen iz dva. Ne mora se pisati 1.41421356237 … Može se zapisati upravo tako, kao √2, kao što se jedna trećina može zapisati kao 1/3, a ne mora se pisati 0,333333333… A kad u operaciji dođe kvadriranje rezultat će se vratiti na 2.

Na primjedbu da nije problem u načinu zapisivanja nego u nesumjerljivosti između 1 i √2[ix], odgovor bi mogao biti: nesumjerljivost nije problem nego fakt, poznat i u Kini i Indiji, kako tvrde Chemla i drugi[x]. Na kalkulaciji, koja je na Istoku prioritet, je da iziđe nakraj s tim faktom. Što je nesumjerljivost kad se umjesto geometrijski izrazi u decimalnom brojevnom sustavu? To što se može dokazati da se u zapisivanju u decimalnom sustavu rezultata korijena iz dva ne može uspostaviti obrazac, dok se u zapisivanju rezultata 1/3 može ustanoviti obrazac 0,333333…  Zapisan kao 1.41421356237 … korijen iz dva eventualno približno kalkulabilan a zapisan kao √2 može biti kalkulabilan. Način zapisivanja brojeva nije neutralan s obzirom na matematičke operacije.

VII

Pojam ‘matematička kultura’ Chemla eksplicite ograničava na način i kontekst bilježenja i izvođenja matematičkih operacija. Matematičku kulturu ona ne poopćava na kinesku, mezopotamijsku, indijsku, zapadnu i ne povezuje je izravno s drugim elementima kulture, s političkim ili ekonomskim odnosima, običajima, umjetnošću, načinom ophođenja ili pristupom rješavanju konflikata. Matematičku kulturu konkretizira na sadržaj i izvedbu matematičkih operacija u određenom razdoblju i u određenoj sredini, na primjer na kineskom dvoru, u administraciji, u edukaciji, u trgovini. Sugerira da se razvoj brojevnih sustava u Kini isprepletao s onim u Indiji, i da su se decimalni sustavi s mjesnom vrijednošću broja počeli koristiti za posebne matematičke operacije otprilike u istom razdoblju i na Istoku i u arapskom svijetu, a odakle su se proširili na europski Zapad.

Upućuje na matematičku praksu mezopotamskih trgovaca, koji su tijekom stoljeća razvili tehnike preračunavanja iz jednih mjernih jedinica u druge, a koje su se koristile u sredinama među kojima su trgovali. Na primjer površina zasijana žitom se preračunava u posude u koje se nakon žetve sprema, koje su najčešće različitih veličina i omjera (bačva, vrč itd), a koje se raspoređuju kao plaća, porez ili za skladište. Za izračune su postojale formule. Chemla ne spominje novac, no s njime je izazov zacijelo složeniji. S jedne strane sažeto bilježenje količina omogućava matematičke operacije, s druge strane preračunavanje zahtijeva matematičku ekspertizu, koja se čuvala od drugih. Matematika ne teži po sebi transparetnosti i razumljivosti svima. Kad bi Karine Chemla govorila općenito o kineskoj matematičkoj kulturi anulirala bi povijest matematike, zanemarila utjecaje iz drugih sredina i minimizirala značenje materijalnih izvora; zaključivala bi iz upitnih generalnih tumačenja.

To ne znači da se rezultatima njezinih i drugih sličnih istraživanja neki već ne koriste za uglavnom (još?) nedovoljno utemeljeno poopćavanje i podjele na zapadnu kolonijalnu i matematike koloniziranih sredina. Sama Chemla ne ide toliko daleko, iako neskriveno želi reafirmirati druge matematičke pristupe, druge povijesti i drukčija shvaćanja matematike. Ta ideja uzima sve više maha i nije neizostavno sastavnica onoga što se naziva woke kulturom, nego je često iskrena matematička, povijesna i filozofska znatiželja.

VIII

Perspektiva daljnjih istraživanja matematike izvan Zapadnog svijeta nije saglediva ako bi ostala na iskopavanju sve novih i novih pojedinosti čija signifikantnost nije uvijek jasna. Jedna je stvar dovesti u pitanje dosad prevladavajući narativ o matematici, njezinoj povijesti i širenju koje se situira u jačanje zapadne kulturne, ekonomske i sve druge dominacije, a druga stvar destilirati novu sintezu iz sve sile puteva kojima je Chemla krenula, a da se ne upadne u drugi ideološki apriorizam[xi]. Najnovija ‘dekolonizacija matematike’, započela je sad već prije četiri desetljeća (iako je neki prepoznaju i u radovima s početka 19. stoljeća), a u posljednje vrijeme čak uzima maha[xii].

Sve više znanstvenih radova bavi se tradicionalnom i domorodačkom matematikom (Iz rada u bilješci xii: Hongzhang Xu and Rowena Ball (2023): Multiple Forms of Knowing in Mathematics: A Scoping Literature Study)

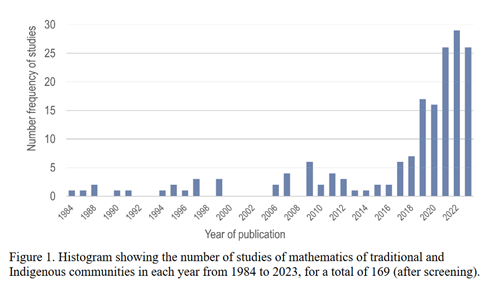
Zasad se u njoj najviše vidi da ni matematici, odnosno matematičkoj zajednici, nije strano kretanje od preduvjerenja. Govori se o matematičkim sektama i matematici kao kultu. Pravoj znatiželji to je odbojno. Ali, kao i u drugim disciplinama i u radovima koji matematiku ‘dekoloniziraju’ zna biti zapažanja za probrati (što zahtijeva poseban članak). Odmahivanje rukom na tu mogućnost je iritantno, odnosno – kolonijalni pristup.

Istraživanja razvoja matematike u različitim sredinama izaziva barem dva pitanja.

Prvo – je li matematičkom obrazovanju primjerena uniformnost? Matematika se u različitim sredinama već poučava na različite načine, kao što se u povijesti poučavala drukčije nego danas, ali pitanje je li matematičkom obrazovanju uniformnost uopće primjerena ne afirmira samo različite matematiče tradicije nego vodi priznavanju različitosti kao bitnoj karakteristici matematike. Matematičke prakse i koncepti širili su se od Istoka do Zapada i natrag, oduvijek. Sad je već široko prihvaćeno da je pojam ‘zapadna civilizacija’ konstrukcija formulirana u 19. stoljeću[xiii], a da Antika, iz koje je po toj konstrukciji Zapad potekao, uopće nije bila jedinstvena na način da je bila suprotstavljena okolnim ‘civilizacijama’, nego je s njima bila snažno isprepletena. Matematičke prakse su inertne, ali radi se o prožimanju kultura u razdoblju od nekoliko tisuća godina. Nula iz Indije ili arapski brojevi, na Zapad nisu preneseni kao kuga, na nekom brodu sa štakorima, nego je to trajalo. Po tim uvidima o blagotvornom prožimanju matematičkih kultura i Chemla pripada u ‘dekolonizatore’, ali ‘dekolonizacija’ uključuje i prihvaćanje da su različiti putevi razvoja primjereni matematici.

Drugo, matematika na Zapadu danas svakako nije superiorna na svjetskoj razini, ili barem nije onako kako je nekad bila. Matematičari Dalekog Istoka su brojni i vrhunski. Je li to zbog tradicije, ili zato što je u 20 stoljeću na Daleki Istok a osobito u Kinu napokon prodrla zapadna matematika? Ili zbog oboje? No, što je uopće superiornost u matematici, koja je toliko raznolika da ni specijalisti u jednom području nemaju pojma o drugom, kako tvrdi Kevin Buzzard (Imperial College London). Slično je naravno i u drugim znanstvenim disciplinama. Pitanje superiornosti je to intrigantnije shvati li se matematiku kao praktičnu disciplinu, kako je shvaća Chemla, a ne kao teoriju, čisti zor, koje se mišljenje o matematici uvriježilo od Platona[xiv].

Kod Chemlae matematika nije praktična samo po primjeni u administraciji i trgovini, nego je to disciplina kojom se nešto pravi, kao što se pravi košara od pruća. Prave se, vidjeli smo, brojevni sustavi, uređaji za računanje, konstruiraju se matematički svjetovi i teorije. Povijest raznolikost matematičkih kultura na svoj način potvrđuju da je riječ o praktičnoj disciplini (u području čistog zora)[xv].

IX

Napokon, nužna završna napomena: čitanje Karine Chemla je vrlo zahtjevno. U spomenutom dugom uvodu u zbornik o povijesti računanja i kvantifikacije ima puno mjesta na kojima iznese neku tezu, sugerira mogući zaključak a onda se ogradi upozorenjem da je to potrebno još istraživati. Nerijetko navede da će o tvrdnji ili zaključku koji je izvela poslije još raspravljati, što naravno otežava praćenje teksta, no još je nezgodnije što u toj kasnijoj raspravi, kad se do nje dođe i čitatelj se sjeti da je o tome već pisala, ne donese ništa novo nego tek ponovi prethodni zaključak.

Zna biti namjerno neodređena. Spomene da neki zaključak ovisi o različitim kontekstima i okolnostima i da u njima ima različito značenje, ali ne precizira ni što misli pod kontekstima ni pod okolnostima ni koja različita značenja zaključak u njima poprima. Izrazitu pažnju posvećuje pojedinostima, ispituje ih jednu za drugom, skupi ih mnoštvo, a da njihovo mjesto u nekoj široj slici nije jasno. Mnoge detalje kao da navodi radi korektnosti prikaza a da ni na koji način nisu utkani u sintezu, nego su tu, kao konci ostavljeni da vise s tkanja koje bi trebalo utkati ili odrezati.

To su naravno zamjerke, ali postoji i opravdanje, kakvo-takvo. Prije svega, riječ je o toliko novom pristupu komparativnoj povijesti matematike da se može reći da se njime otvara i novo područje, u koje je iz raznih smjerova nahrupilo mnoštvo istraživača. Chemla se oslanja najviše na pažljivo čitanje dokumenata koji su nekako preživjeli tisućljeća, uglavnom u prijepisima koje se mora uzimati s rezervom, a pitanje je i što su značili u trenutku u kojem su nastajali. Svaki originalni materijal, na koji se Chemla prvenstveno oslanja, neizbježno je necjelovit. Chemla puno vremena i prostora troši na opovrgavanje dosadašnje povijesti matematike, na tumačenja u kojima se današnja shvaćanja i predodžbe projiciraju u davno doba te na zaključke koji se izvode iz dekontekstualiziranih uvida. Često ulazi u digresije i usko specijalizirane rasprave. Zbog toga je realna mogućnost da ovaj prikaz sadrži tumačenja s kojima se ne bi (u potpunosti) složila. Stvari ispituje iz toliko aspekata da koherentna slika kao da izmiče i njoj samoj. No, pojedinosti koje zamornim iskopavanjem i čišćenjem starih udžbenika, i tumačenjem komentatora Karine Chemla iznosi na vidjelo nisu tako bezazlene, kao ni proučavanje, promjena i potencijalnih utjecaja među matematičkim kulturama. Njihovo je značenje poticajno, čak i više nego dokumentarno. U ovom je članku prvenstveno riječ o nastanku i pojmu broja, a razmatranje istraživanja komparativne povijesti matematike iz raznovrsnih izvora čini se produktivnim putem da se o tome stekne predodžba koja je uvjerljiva, a svježa u odnosu na dosadašnje filozofske i matematičke rasprave.

• Bilješke

[i] Istina je ovdje pod navodnicima kao podsjetnik na to da je prema korespondencijskoj teoriji istina (odnosno istinita) tvrdnja koja je adekvatna onome što tvrdi, na primjer kad se kaže ‘ono je kuća’, a ono je stvarno kuća. Kod matematičke istine da je 2 + 2 = 4 zna se tvrdnja, da je dakle  2 + 2 = 4, ali je pitanje o čemu je, što je izvan te tvrdnje na koju se ona odnosi i istinito je predstavlja. Korespondencijska teorija je izdvojena jer je vjerojatno najraširenije, ali svakako najuobičajenije, shvaćanje istine.

[ii] Stephen Chrisomalis se u knjizi Reckonings: Numeral, Cognition, and History (MIT, 2020) bavi objema spomenutim temama, matematičkom spoznajom i poviješću matematičke numeracije.

[iii] Chrisomalis, ibid, zaključuje da računanje služi evaluaciji, da (broju) pridruži vrijednost.

[iv] I danas u mnogim jezicima ‘kvadriranje’ izravno asocira na geometrijski lik.

[v] Zvonimir Šikić u članku o von Neumannovim rednim i glavnim brojevima, misli da ‘jedinstveni koncept broja ne postoji’. Z. Šikić: What are numbers? International studies in the philosophy of science, Vol. 10, No 2, 1996. Šikićeva je tema ustvari sljedivost, jedna od ključnih karakteristika brojeva i postulat Peanove aritmetike, ali se ovdje time ne bavimo.

[vi] Posebna je tema, koja se ovdje nameće, a povezuje matematiku i brojeve s nekom vrstom pravednosti, jednakosti, jer omogućuju usporedbe.

[vii] Vidi, Stephen Chrisomalis, Numerical Notations: A Comparative History; Cambridge University Press, 2010

[viii] Stillwell, The Story of Proof (Princeton University Press, 2022)

[ix] Zvonimir Šikić je u prvoj varijanti članka na ovom mjestu iznio primjedbu: „Ne razumijem gdje je razlika. To je tako i za Grke. Problem je nesumjerljivost od 1 i √2 a ne kako su zapisani.” Na tu smo primjedbu nastojali odgovoriti u ovoj varijanti članka.

[x] Matematičke operacije usložnjuju shvaćanje beskonačnosti, pojma koji se u matematici intenzivno istražuje. Negativni su brojevi, piše Chemla, ishod rješavanja linearnih jednadžbi. Sustav racionalnih brojeva koji nastaju dijeljenjem uključuje beskonačno male veličine na način da se između dva racionalna broja uvijek može smjestiti barem još jedan. Napokon, realni brojevi, među kojima je i √2, uključuju svoj tip infinitezimalnih veličina. U sustavu prirodnih i cijelih brojeva, a osobito u geometriji, pojam beskonačnosti je očito različit, iako na svoj način i isti. O realnim brojevima da se i ne govori. Imaju i svoje notifikacije. Neizbježna beskonačnost na specifičan je način sastavnica svih tih sustava koji su – praktična konstrukcija, ishod matematičkih operacija.

[xi] Vidi Alan J. Bishop: Western mathematics: the secret weapon of cultural imperilism, Race Class 1990

[xii] Hongzhang Xu and Rowena Ball (2023): Multiple Forms of Knowing in Mathematics: A Scoping Literature Study, Mathematical Sciences Institute, Australian National University; Hongzhang Xu and Rowena Ball (2022): Is the study of Indigenous mathematics ill-directed or beneficial? Link: https://arxiv.org/abs/2212.02778

[xiii] Josephine Quinn (2024): How the World Made the West, Bloomsbury Publishing

[xiv] Serafina Cuomo u istraživanju matematike i tehnike u zapadnoj Antici također je ustanovila da matematika nije bila shvaćana samo kao platonistička teorija nego i kao techne, jedna vrsta praktičnog znanja. Vidi: Kako su oni sve to znali? Duboki rudnik antičke matematike.

[xv] U praktičnoj konstrukciji matematičkih svjetova ipak se slijede neka pravila, kao što se moraju slijediti kad se rade košare od pruća. Koja? Jesu li vječna i svima ista? Rasprava između matematičkih platonista/realista, formalista, naturalista, fikcionalista, nikad neće biti završena, jer matematika izgleda uvjerljivo iz svih tih aspekata. Pri tome oni koji zauzimaju strane na svoj generalni pogled često skaču sa slabog oslonca, nekog priručnog primjera, nekog ishitrenog zaključka. Vidi Horsten, Leon, “Philosophy of Mathematics”, The Stanford Encyclopedia of Philosophy (Winter 2023 Edition), Edward N. Zalta & Uri Nodelman (eds.), URL = <https://plato.stanford.edu/archives/win2023/entries/philosophy-mathematics/>.