Je li matematika Zapada superiorna matematici Istoka?

Tijekom povijesti a i danas u različitim se dijelovima svijeta matematika drukčije prakticirala. Francuska povjesničarka matematike i filozofkinja Karine Chemla smatra te razlike bitnima za razumijevanje prirode matematike. No, suprotstavlja se predodžbi prema kojoj je matematika na Zapadu superiorna matematici Istoka. Željko Ivanković prikazuje njezin zbornik o povijesti matematičkog dokaza na Istoku i Zapadu u kojem objašnjava i razlike između tih matematičkih kultura.

• Naslovna fotografija: Detalj naslovnice zbornika The History of Mathematical Proof in Ancient Traditions

I

U uvodu zborniku o povijesti matematičkog dokaza, u kojem uspoređuje matematiku antičke Grčke s onom u ranim kulturama ili civilizacijama Istoka – Babilonu, Indiji i Kini, Karine Chemla, afirmirana francuska povjesničarka i filozofkinja matematike ističe intrigantnu i višestruko ilustrativnu epizodu[1]. Potkraj 16. stoljeća kršćanski su misionari dospjeli na južne granice Kine. U strategiji evangelizacije isusovca Mattea Riccija temeljnu je ulogu imao prikaz dosega europske znanosti, kojima je namjeravao privući kinesku obrazovanu klasu. Jedan od prvih i najvažnijih pothvata bilo je kinesko izdanje Euklidovih Elemenata 1607. godine. Preveli su ih Ricci, koji je Euklida studirao u Rimu, i Xu Guangqi, visoko pozicionirani pripadnik kineske administracije koji je već bio prešao na kršćanstvo.

Prema Chemla prijevod Euklida na kineski imao je dva glavna cilja. Prvi je demonstracija geometrijskog znanja u Elementima koje je Ricci smatrao superiornim tadašnjoj kineskoj matematičkoj praksi. Talijanski je isusovac očekivao da će znanje geometrije biti prihvaćeno kao prednost europskih misionara, a što će omogućiti da i njihov ostali nauk lakše prolazi. Drugi je, naime, cilj bio da se uz pomoć Euklidove metode afirmira kršćanska teologija, učenje o kršćanskom bogu. S obzirom na suvremeno shvaćanje odnosa (matematizirane) znanosti i teologije Riccijev je plan neočekivan.

Matematika, koja se razvila iz euklidskog pristupa, u temelju je zapadne znanstvene metode. Najslavnija i eksplicitna ilustracija je Newtonova Philosophiae naturalis principia mathematica (prikaz/filozofija prirode matematičkom metodom). U okruženju u kojem je zavladao ‘racionalni i znanstveni’ način mišljenja, razrasle su se industrijska i tržišna ekonomija, a zahvaljujući kojima je Zapad počeo dominirati svijetom. Glavninu je svoje forme takva (re)konstrukcija moderne povijesti dobila u 19. stoljeću i značajno se održala do danas. Nakon dugih stoljeća samopotvrđivanja moderna je znanost dakle napokon preuzela duhovno prijestolje u društvu u kojem je prakticirana. Obično se smatra da je smijenila religiju. No prema isusovcu Ricciju u euklidskoj se metodi našla (prepoznala se) i kršćanska teologija. To ustvari ne čudi:  u 17. stoljeću Spinoza i etiku izvodi ‘modo geometrico’. Euklidska se metoda raširila kao sveprimjenjiva, univerzalna[2]. U nekim je interpretacijama i totalizirajuća, no koliko je to ‘obojena’ karakterizacija za drugu je raspravu. Zasad je zaustaviti se na matematici.

Ni povijest matematike, ni razlike među matematičkim kulturama nisu nimalo nebitne za razumijevanje prirode matematike. Karine Chemla (https://www.radcliffe.harvard.edu/people/karine-chemla)

Chemla je epizodu s  Euklidom i kršćanskim misionarima u Kini opisala u zborniku The History of Mathematical Proof In Ancient Tradition (Cambridge University Press, 2012), koji je uredila, napisala problemski i pregledni Uvod te članak o dokazu u matematici drevne Kine. Zbornik se bavi, ustvari – nastoji opovrgnuti tezu da u matematikama izvan zapadnog kruga praktički uopće nije bilo dokaza, a posebno da nije bilo dokaza euklidskog tipa, koji se na Zapadu smatrao i još često smatra jedinim pravim. Euklidskom se metodom dokazuju teoremi kao što je najslavniji – Pitagorin poučak.  Deduciraju se neupitnom logikom (kako je opisana u Aristotelovom Organonu u knjizi Prior Analytics) iz definicija i aksioma – tvrdnji koje su svima očito istinite i s kojima se svi slažu. Uzima se da istinitost tvrdnji iz teorema demonstrirana ili potvrđena na taj način vrijedi – uvijek i svugdje. Tako je u temeljima zapadne matematike geometrija[3]. Istočna se matematika, s druge strane, predstavlja kao – puko računanje, kao dominantno aritmetika. Računanje se uzima kao inferiorno geometriji, ponavlja Chemla u niz navrata. Iako aritmetike, naravno, ima već i u Elementima, a i na Istoku se neminovno bave i geometrijom, na primjer izračunom površine i volumena.

No ovdje se radi o metodi ali i o opisu društva. Iz osnovnih teza o postojanju/nepostojanju dokaza i razlike geometrijskog (teorijskog) i računskog (praktičnog) pristupa izvedene su druge, ‘kulturološke’ razlike zapadne i istočne matematike. Prema njima, u istočnoj se matematici postupci izračuna zadataka (današnjim rječnikom – algoritmi) jednostavno prenose s koljena na koljeno, od učitelja na učenika, primjenjuju se slijepo, kako su propisani u administrativnim procedurama, ne propituju se i ne dokazuju. Društvo neupitne hijerarhije. Kao da su ti postupci nastali nasumce, kao da u tim školama i administraciji nije bilo sumnje[4].

Prema raširenoj predodžbi matematika je uvijek ista za sve, a matematičke istine vječne. Jednom dokazan Pitagorin je poučak dokazan zauvijek. Stoga se i povijest matematike smatra manje bitnom. U obrazovanju, od vrtićkog do visokoškolskog, matematici se najčešće pristupa kao da i nema povijest[5]. Čemu znanje o pokušajima, neuspjesima, zastranjenjima i usavršavanjima, nakon što se otkrije, spozna i nauči konačni i univerzalan zaključak. Povijest matematike se u Hrvatskoj može studirati samo na nastavničkom smjeru zagrebačkog PMF-a, koji upisuje malo studenata, i to kao izborni predmet.

Pitanje je li povijest matematike mogla biti drukčija ili je – sukladno determinističkoj prirodi same matematike –  onakva kakva je morala biti, ipak je neizbježno. Ako je moglo biti drukčije zašto nije, nego se matematika razvijala baš kako se razvijala i razvija? Slijedi li taj razvoj neku pravilnost? Drugo, matematičke su prakse vidljivo različite ne samo kroz povijest nego i u različitim kulturama i ‘civilizacijama’. No i te se razlike za prirodu matematike najčešće smatraju akcidentalnima.

Karine Chemla ta dva pitanja ne smatra akcidentalnima: ni povijest matematike  ni pitanje ima li štogod značajno u različitosti matematičkih kultura? Naprotiv, iz uvida koje stječe u istraživanjima izvodi i neke dalekosežne zaključke o prirodi matematike.

U nastavku se članka prvo predstavlja njezina najznačajnija bibliografija. Slijedi prikaz njezina istraživanja o dokazu u kineskoj matematici koje se zanimljivo uklapa u suvremene rasprave o matematičkom dokazu. Kao da se neka pitanja neprestano ponavljaju, a matematika je nesavršena i možda nezavršiva. U zaključku se otvara pitanje je li i potiskivanje povijesti matematike sastavnica specifičnog odnosa prema matematici, dakle svojevrsna matematička kultura. (U sljedećem će članku biti predstavljena njezina intrigantna rasprava o povijesti brojeva, koja reafirmira povijest matematike upravo iz proučavanja matematičkih praksi u različitim kulturama.)

II

Intenzitet rada Karine Chemla je zavidan. Najvažniji su zbornici u kojima je redovito vodeća urednica i uvijek i jedna od autorica. Fokusirani su na izabranu istraživačku temu oko koje se okupi skupina autora, koji prije pisanja članaka za zbornik nerijetko diskutiraju u radnim skupinama ili na konferencijama. To je sve češća metoda znanstvene produkcije. Kako je po obrazovanju matematičarka i filozofkinja Chemla se, a ni mnogi drugi autori u njezinim zbornicima, ne suzdržavaju od filozofskih zaključaka. Dojam je da su upravo filozofski zaključci o matematici i matematičkoj praksi cilj njezinih istraživanja. No do njih ne dolazi pogledom s visine, iz ptičje perspektive, nego ih nastoji uočiti i izvesti iz konkretnog povijesnog materijala kojem se teži maksimalno približiti. U zbornicima koje je Chemla uredila raspravlja se, ponajprije iz povijesne perspektive: o znanstvenom tekstu kao povijesnom izvoru, o matematici i mjerenju, o matematici u praksi – u administraciji i ekonomiji, o prijepisima i komentarima matematičkih spoznaja i postupaka, o generalizaciji u matematici i znanostima, o postupcima (tehnikama) računanja u antičko doba i kasnije i o dokazu ispravnosti tih postupaka, o povijesti brojeva.

Iako je već 2004. godine uredila Springerov zbornik History of Science History of Text, njezine profesionalne biografije puno više ističu već spomenuti zbornik The History of Mathematical Proof In Ancient Tradition (Cambridge University Press, 2012). Radi se o tome da je prvi zbornik orijentiran usko prema metodi interpretacije teksta u povijesti znanosti, a drugi na povijesnom materijalu propituje i pojam dokaza. Zanimljivo, afirmirani matematičar John Stillwell objavio je 2022. The Story of Proof: Logic and the History of Mathematic (Princeton University Press), zato što, prema njegovim riječima, problemu matematičkog dokaza nije posvećena dovoljna pažnja.

Stillwell možda nije u pravu. Prema Filozofiji matematike Joela Hamkinsa koju smo ovdje prikazali, matematičari (i filozofi) o dokazu pišu puno, ali i divergentno. Stoga se pitanja što su dokazom i dokazanim smatrali matematičari drevnih kultura od Kine do Grčke uklapa u raspravu (iako se time problem možda dodatno komplicira). S druge strane, Stillwell je svojevrsni kontrapod Karine Chemla. U knjizi inzistira na razlici zapadne i istočne matematike, geometrijskog i računskog pristupa. U gornjem videu je izlaganje, kojem ćemo se u članku vraćati, a u kojem na sveučilištu Princeton predstavlja teze iz knjige.

Nakon uspjeha zbornika o povijesti dokaza uslijedila je još nekolicina podebelih zbornika. Za Oxford University Press Chemla, Renaud Chorlay, i David Rabouin uredili su 2016. zbornik o generalizaciji u matematici i znanostima. S kolegicama Agathe Keller i Christine Proust urednica je cijele Springerove serije o tome zašto su važne znanosti antičkog doba.  Sve tri dolaze iz Nacionalnog centra za znanstvena istraživanja (CNRS – Centre national de la recherche scientifique), svojevrsnog francuskog pandana Institutu Ruđer Bošković, centralnog nacionalnog instituta koji međutim, kao što vidimo, uključuje i istraživanja izvan prirodnih znanosti.

U toj je seriji 2022. godine s Keller i Proust uredila Cultures of Computation and Quantification in the Ancient World Numbers, Measurements, and Operations in Documents from Mesopotamia, China and South Asia iz 2022. godine, za koji je napisala uvodnik od 130 gusto tipkanih stranica i dugo poglavlje o porijeklu brojeva i računanja u Kini, a dvije godine prije Cécile Michel i Chemla napisale su uvodnik i uredile zbornik Mathematics, Administrative and Economic Activities in Ancient Worlds.  Chemla je napisala poglavlje o  korištenju volumena u mjerenju žita u ranoj imperijalnoj Kini. Napokon, Chemla i Glenn W. Most uredili su zbornik Mathematical Commentaries in the Ancient World. A Global Perspective, (Cambridge University Press, 2022).

Zbornici koje je (su)uredila Karine Chemla

III

Kako dakle stoje stvari s dokazom u drevnoj kineskoj matematici? U spomenutom zborniku Chemla, u šezdesetak stranica dugom članku pod naslovom Reading proofs in Chinese commentaries: algebraic proofs in an algorithmic context analizira izračun volumena ‘krnje piramide s kružnom osnovom’, kako je prikazan u Devet poglavlja o matematičkoj proceduri, udžbeniku kineskih matematičara kompiliranom u prvom stoljeću nove ere. ‘Krnja piramida s kružnom osnovom’ je naravno krnji stožac. Prema Chemli, nije riječ ni o kakvoj konfuziji, kamoli o neznanju, nego naprosto o tadašnjoj terminologiji: ono što zovemo piramidom u Kini se tada nazivalo ‘piramidom s kvadratnom osnovom’. Udžbenik Devet poglavlja o matematičkoj proceduri u drugoj je polovici trećeg stoljeća komentirao matematičar Liu Hui, toliko utjecajno da je komentar zapravo postao sastavni dio udžbenika u koji su u sedmom stoljeću uvrštena i objašnjenja skupine znanstvenika koje je nadgledao Li Chunfeng.

Uostalom, ‘originalno izdanje’ i nije preživjelo. Izdanje s tim komentarima i objašnjenjima predmet je analize Karine Chemla, budući da je, prema autorici, Liu Hui ustvari nastojao pokazati odnosno dokazati ispravnost procedure izračuna ne samo u ovom nego i u drugim zadatcima. Kineski su matematičari dakle, prema Chemla, raspravljali o ispravnosti procedure, dokazivali je i – kako koji put – u tome uspijevali. Je li Liu Hui zaista dokazao ispravnost formule sad je manje važno. Bitno je da je nije dokazao na opisani euklidski način, iz nekih početnih premisa. Kako ju je onda dokazao?

­ ­

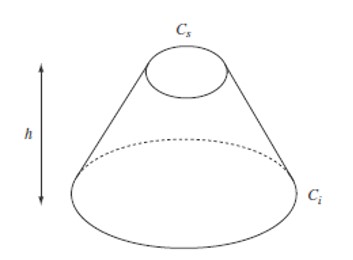
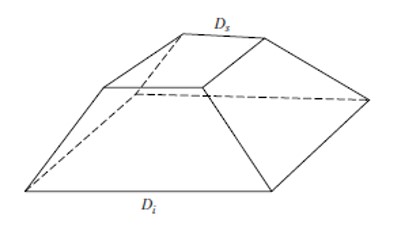
Zadatak koji je predmet analize glasi: „Pretpostavimo krnji stožac s opsegom doljnje kružnice 3 zhanga, a opsegom gornje kružnice 2 zhanga i visinom 1 zhang. Koliki je obujam? Odgovor je 527 chi i 7/9 chi.“  Iza zadatka odmah slijedi algoritam koji glasi: „Pomnože se opsezi doljnje i gornje kružnice, zatim se svaki opseg pomnoži sam sa sobom, ti se rezultati zbroje i pomnože visinom stošca i podijele s 36.“ Zhang je kineska mjera za dužinu jednaka 3,58 metara. Chi je deset puta manji: 1 zhang = 10 chi. Omjer opsega i dijametra kružnice uzimao se kao 3:1, sa sviješću da je to približno.

Prema Chemla, algoritam je niz operacija koje se primjenjuju na dane podatke da se dobije željena veličina.  Liu Hui prvo uočava algoritam, operacije i proceduru izračuna zadanog volumena. Zatim poseže za algoritmom čija je ispravnost već dokazana (i to u odjeljku koji neposredno prethodi zadatku). Riječ je o izračunu volumena krnje piramide s kvadratnom bazom. Zadani stožac se upiše u tu piramidu tako da su stranice gornjeg i donjeg kvadrata jednake dijametrima (gornje i donje) kružnice. Kako je u zadatku dan opseg kružnica krnjeg stošca, dijametar se dobije tako da se opseg podijeli sa 3. Također se uzima da je odnos površine upisane kružnice i površine kvadrata ¾. Kad se sve to uzme u obzir dobije se prije navedeni algoritam za izračun volumena krnjeg stošca.

Već se ovdje može zaključivati da je Liu Hui algoritam nastojao dokazati. Prvo, za izračun volumena stošca koristi se analogijom s izračunom volumena piramide. Zatim, koristi se već dokazanim algoritmom/formulom. No ključna teorijska vrijednost komentara koje analizira za Chemlu je nastojanje da se postigne općenitost (generality, čime se bavila u posebnom zborniku), odnosno pokušaj da se izračun poopći tako da se može koristiti i u nekim sljedećim izračunima. Uostalom, već dokazane formule kojima se koristi i analogije na koje se oslanja Liu Hui uzima kao da imaju taj karakter općenitosti.

Liu Hui se koristi kraćenjem i množenjem razlomaka istim brojem, svođenjem na zajednički nazivnik radi zbrajanja i zamjenom redoslijeda operacija (množenja i dijeljenja). Chemla naglašava da on nastoji pokazati opravdanost tih operacija a sve ne bi li se postupke učinilo jasnima, razumljivima i logičnima. Ali i preglednima. Neke operacije izračuna volumena krnjeg stošca imaju grafički aspekt.

O čemu se radi možda je najbolje (jer je najlakše) objasniti na primjeru koji bi svima morao biti poznat, na množenju višeznamenkastih brojeva. U jednom obliku postupka množenik prvo množimo jedinicama množitelja, zapišemo jedinice iz rezultata a desetice zapamtimo ili zabilježimo sa strane, ili iznad desetica da ih uračunamo kad množenik pomnožimo deseticama. Bilježenje na marginu Chemla nalazi u mnogim ranim kineskim matematičkim spisima i vrlo joj je važno i za raspravu o povijesti brojeva. Postupak kao s deseticama ponavlja se sa stoticama itd. Brojevi se slažu u prepoznatljivi grafički oblik na koji se korisnik postupka, učenik ili službenik u državnoj administraciji navikne. Matematika je vježba, ona ‘legne’. Ali, pogledamo li postupak pažljivije i on i njegov grafički lik izgledaju ne samo preglednim nego i logičnim, očigledno ispravnim. Preglednost i očitost načini su dokazivanja ispravnosti postupka, koji su – tvrdi Chemla – primjenjivani i u drevnoj Kini.

Množenje velikih brojeva ima prepoznatljiv grafički oblik, koristi se bilježenjem brojeva na margini, a sve radi jasnoće i razumljivosti, koji su kriterij dokaza da je postupak ispravan. Primjer s Wikipedije

Liu Hui postupak izračuna volumena krnjeg stošca nastoji dakle prikazati jasnim, preglednim, razumljivim i logičnim, primjerenim cilju. Chemla je naglasila i da je intencionalno svodio operacije na elementarne, na one koje smatramo neupitnima koje imaju osobinu općenitosti i koje su upravo najpogodnije za dokazivanje drugih postupaka. To je naoko slično dokazivanju teorema iz aksioma, iz početnih neupitnih tvrdnji i definicija. Ali nije isto. U euklidskoj geometriji veličina kvadrata nad hipotenuzom može se izračunati koristeći se Pitagorinim poučkom, koji je prije izveden iz definicija i postulata i dokazan kao istinit. Liu Hui svodi postupak na elementarne aritmetičke operacije koje ipak nisu izvedene iz aksioma. Naravno, nisu ni mogle biti izvedene iz aksioma. Aritmetika je aksiomatizirana kao Dedekind/Peano aritmetika tek potkraj 19./početkom 20. stoljeća pa ni u aritmetici Antičke Grčke nije bilo dokaza na temelju aksioma.

Liu Hui svodi postupak na elementarne aritmetičke operacije koje ipak nisu izvedene iz aksioma.

Ali, matematičari znaju, a i Stillwell primjećuje, da ni danas matematičari ne dokazuju ispravnost matematičkih formula ab ovo, od Peano-aksioma, jer su oni ustvari elementarni opis prirodnih brojeva pomoću kojeg se mogu predstaviti aritmetičke operacije[6]. Pogledajte drugi Stillwellov video od 15. minute nadalje:

Kako matematikom objasniti izvanzemaljcima da smo inteligentni: John Stillwell

Svrha dokaza je razumijevanje a ne verifikacija, podsjeća Arnold Ross[7]. Čak i kad je ispravnost postupka dokazana, pitanje je kako onaj tko ga primjenjuje zna da ga je korektno primijenio, da je rezultat točan. U slučaju množenja višeznamenkastih brojeva umnožak se zna podijeliti množiteljem da se provjeri hoće li se dobiti množenik. Iako je uglavnom efikasno, to je cirkularno, množenje se provjerava dijeljenjem a dijeljenje množenjem. Svejedno se kod složenijih izračuna točnost rezultata, a posredno i postupka, ipak provjerava inverznom operacijom. Chemla je i to našla kod Kineza.

Liu Hui postupak za izračun volumena okrnjenog stošca nije provjeravao ni na način da je izabrao par nasumičnih veličina, uvrstio ih u formulu, izračunao a zatim izmjerio je li dobio točan rezultat, nego je upravo kao što Ross tvrdi, nastojao postupak razumjeti, razjasniti i predočiti kao očigledno ispravan. Ako je u tome uspješan onda verifikacija dokazano ispravnom inverznom operacijom ima smisla.

Karine Chemla izdvojila je iz komentara algoritma za izračun volumena okrnjenog stošca niz elemenata u kojima se može prepoznati svojevrsno dokazivanje. Ono nije euklidsko dokazivanje, koje je Zapad uzimao jedinim valjanim, ali u 20. je i a osobito u 21. stoljeću, dokazivanje u matematici na Zapadu podvrgnuto minucioznoj analizi i relativizirano.

IV

Već je Heraklit inzistirao da su ‘oči i uši varljivi svjedoci onima koji imaju barbarske (nerafinirane, neškolovane) duše’. Tako je i u matematici. Pogleda li se na Wikipediju ili bilo koji udžbenik matematike Pitagorin se poučak najčešće prvo demonstrira vizualno. Pravokutni trokut i kvadrat nad hipotenuzom obgrle se jednim većim kvadratom i onda se premještanjem geometrijskih likova koji su tako iscrtani vidljivo demonstrira da je površina kvadrata nad katetama jednaka površini kvadrata nad hipotenuzom. Vizualnom demonstracijom Pitagorina poučka započinje i Stillwell svoju priču o dokazu. Podsjeća da je porijeklo riječi teorem u ‘onome što vidimo’.

No, u gornjem videu u kojem na Princetonu predstavlja svoju ovdje spomenutu knjigu o dokazu Stillwell upozorava (od 2:20) kako puki vizualni dokaz Pitagorina poučka zavarava i dalje objašnjava da se Pitagorin poučak ima izvesti još i logički (rekli bismo – unutrašnjim okom)  iz geometrijskih aksioma. U Uvodu zbornika o dokazu Chemla podsjeća da, ironično, čak ni Platonova demonstracija udvostručenja površine kvadrata u dijalogu Menon nije izvedena iz aksioma nego je – tek vizualna (str 22, bilj. 15).

Kršćanski misionari u Južnoj Kini na početku 17. stoljeća susreli su se s drugom ‘civilizacijom’. Danas, ‘susret civilizacija’ zna implicirati izvanzemaljce. Matematičari i znanstvenici zamišljaju da bi čovječanstvo iskoristilo matematiku i znanost da i izvanzemaljcima kao Kinezima pokaže da je barem razumno (a ne više superiorno). Na sondu Pioneer, koja je 1972 godine upućena u dubine svemira, slijedom ideje Carla Sagana postavljena je metalna pločica na kojoj su urezani crteži muškarca i žene, položaj našeg planeta u Sunčevu sustavu, kao i struktura i osobine vodika, koji je prema našim današnjim saznanjima najrašireniji element u svemiru. No ako izvanzemaljci do kojih Pioneer dopluta kao boca s porukom bačena u ocean nemaju osjetilo vida, to je kvalitativno drukčije nego kad vizualna demonstracija tek zavarava. Saganova ideja potpuno pada u vodu, osim ako izvanzemaljci ne bi nekako napipali pločicu, shvatili da je to poruka i da je od inteligentnih bića. Što ako poruku ne mogu ni napipati?

Što ako izvanzemaljci nemaju osjetilo vida, kako mogu pročitati poruku na pločici na svemirskoj sondi Pioneer?

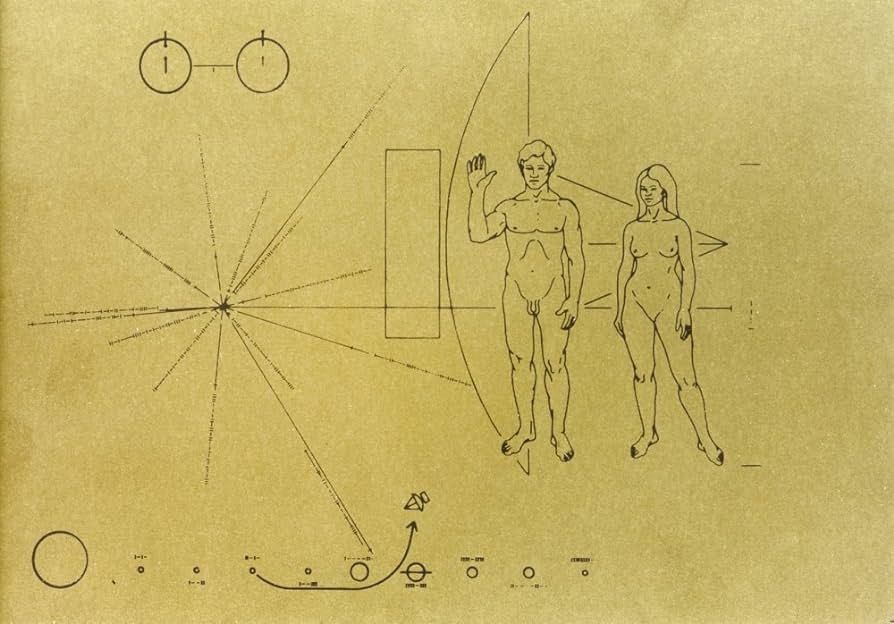
I u predavanju u kojem spekulira o sporazumijevanju s izvanzemaljcima pomoću matematike Stillwell također pretpostavi da oni uopće nemaju osjetilo vida, ali im je ipak nekako moguće prenijeti neku drugu, nevizualnu matematiku u kojoj se može prepoznati da ljudi nemaju barbarske nego rafinirane duše, vrijedne da se protiv njih ne vodi rat (kao što je protiv Kineza vođen Opijumski rat). Peanova aritmetika je, objašnjava Stillwell, nepraktična za izvedbu čak i najjednostavnijih dokaza iz njenih aksioma. Veći je problem s teorijom skupova, koja aksiomatizaciju aritmetike proširuje, to što izvanzemaljci moraju vjerovati (tako je Stillwell rekao – ‘vjerovati’) u aksiom beskonačnosti (25:00). Pojam beskonačnosti naime uključuje neke kompromise.

U predavanju  linkanom u gornjem dijelu članka u kojem predstavlja knjigu o dokazu Stillwell pojašnjava (od 18:00) da se u infinitezimalnom računu (calculus) prelazi preko proturječnosti da je beskonačno mala veličina (dx) jednom različita od nule (kad se njome dijeli) a drugi je put nula (kad je se zanemaruje). Taj algebarski kompromis u geometrijskom izrazu pretpostavlja da je krivulja sastavljena od beskonačno mnogo ravnih linija (što podsjeća na kinesku kružnu piramidu). Ne napadajući tu matematiku, ovime se samo po tko zna koji put uočava da su aksiomi podložni diskusiji. S njima i euklidski tip dokaza.

V

U knjizi The Dialogical Roots of Deduction (Cambridge University Press, 2020) Catarina Dutlih Novaes s Vrije sveučilišta u Amsterdamu dokaz koncipira šire od onoga što se obično podrazumijeva pod strogim matematičkim dokazom. Novaes sistematizira šest vrsta, odnosno šest aspekata dokaza. To su:

1. dokaz kao verifikacija (istinitosti teorema)
2. dokaz kao potvrda (certifikacija); dokaz se mora izložiti sumnjivcima i kad ih dovoljan broj potvrdi da nisu našli grešku onda je certificiran; važno je, naravno i jesu li skeptici respektirani matematičari ili recenzenti u opskurnom časopisu; ili laici, o tome ovisi i koliko je skeptika dovoljno da potvrdi da je dokaz korektan
3. dokaz kao komunikacija i uvjeravanje
4. dokaz kao objašnjenje ne samo da je nešto istinito nego i zašto je istinito
5. dokaz kao inovacija, kad dokaz ponudi novu ideju ili perspektivu; u nekoliko važnih slučajeva u matematici čak je i pogrešan dokaz otvorio novi pogled na problem
6. dokaz kao sistematizacija, kad ujedini ideje koje prije nisu bile prikazane kao povezane

Pogleda li se bolje, ovih šest karakteristika ne pripisuju matematičkom dokazu samo utvrđivanje istine nego i karakteristike kao što su razumljivost, objašnjenje, koje je Chemla našla kod dokazivanja ispravnosti postupka. Razlikovanjem jesu li dokaz certificirali nepristrani stručnjaci, ili oni kojima je u prvom planu interes, recimo karijerni, ili pak laici, matematički se dokaz smješta i u socijalni kontekst[8], kao da se radi o sudskom dokazu. Matematičkim se dokazom izriče i potvrđuje istina koja je neovisna o ljudima, zapisana u zvijezdama. Jednom kad se dokaže, nemoguće ju je dovesti u pitanje za razliku od sudskog dokaza. Matematički smo dokaz skloni smatrati posve drukčijim od sudskog.

Ta se predodžba o matematici pomalo relativizira, iako teško da će biti do kraja dovedena u pitanje. Utjecaj ekonomskog, društvenog odnosno kulturnog okruženja na razvoj matematike prihvaća se i istražuje i na tome inzistira i Chemla. Iz podjele matematike na zapadnu, teorijsku i istočnu praktičnu, izvedene su kulturne razlike. Chemla želi pokazati iskrivljenost te podjele. Ona obrće red stvari: iz kulturnih razlika izvodi različite puteve razvoja matematike koje ne isključuju ni preklapanja, to jest stizanje do istog cilja različitim putevima, ni razmjenu znanja, ni divergencije.

Prema Stillwellu, matematiku Zapada i Istoka podijelilo je otkriće Pitagorejaca da je korijen iz dva iracionalan broj. Na Istoku su ga, tvrdi, ‘previdjeli’, a Zapad je to otkriće prisililo na suočavanje s pojmom beskonačnosti i razvoj dokaza. Chemla i mnogi njezini suradnici pronalaze da je Istok znao da je korijen iz dva iracionalan, ali je izabran drukčiji put razvoja, orijentiran na kalkulaciju u kojoj dokaz postoji, ali je drukčiji nego u geometriji. Iako se oba pristupa oslanjaju na ‘očigledno’. Naime, i Liu Hui svodi proceduru izračuna volumena krnjeg stošca svodi na ono što smatra očitim. I teorem, na primjer Pitagorin poučak, služi kao algoritam (za izračun hipotenuze iz duljine kateta), ali teorem se dokazuje iz aksioma, koji bi trebali biti svima neupitni. Liu Hui ne tvrdi da je ono što ističe kao očito – aksiom. Niti da je dakle procedura izračuna volumena krnjeg stošca teorem[9].

Istraživanjem razvoja pojma broja i načina zapisivanja brojeva Chemla nastoji pokazati da put koji je Istok izabrao nije bio inferioran. Kako broj po nekoj logici stvari prethodi dokazu, zaključci su tog istraživanja intrigantniji i uzbudljiviji, a za filozofiju matematike čine se i dalekosežnijima. Chemla nastoji opovrgnuti teze, za koje pokazuje da su dominantne na Zapadu, da je broj zapis lingvističke prakse i da nastaje apstrahiranjem. Razvoj heksadecimalnog i decimalnog sustava i mjesne vrijednosti broja povezuje s razvojem kalkulacije. No, to je tema sljedećeg članka o istraživanju najstarije povijesti matematike u radovima Karine Chemla.

• Bilješke

[1] Inicijalna verzija ovog prikaza rada Karine Chemla objavljena je u dva eseja u emisiji Ogledi i rasprave na Trećem programu Hrvatskog radija, koji su dostupni na poveznicama: Povijest dokaza i Povijest matematičkog dokaza;

[2] Politologija Hobbesa, Lockea, Rousseaua, polazi od ‘prirodnog stanja’, uklapa se dakle u novovjeku znanstvenu metodu, kao i Rawlsov misaoni eksperiment sa ‘velom neznanja’ ili Nozickova početna premisa – aksiom, da ‘ljudi imaju prava’.

[3] U dva eseja o radu talijanske povjesničarke i filizofkinje Serafine Cuomo prikazali smo u dva eseja o antičkoj matematici (Kako su oni sve to znali? Duboki rudnik antičke matematike) i tehnologiji (U Antici su tehnologiju bolje razumjeli nego mi danas. Svi Prometejevi darovi). I oni su svoju incijalnu verziju imali na Trećem programu Hrvatskog radija.

[4] Jedan od starih profesora filozofije na Filozofskom fakultetu u Zagrebu u vrijeme buma japanske računalne industrije prije četiri desetljeća, znao je reći da se Japanci računalom služe kao sjekirom, dakle bez razumijevanja zašto njihovo oruđe funkcionira kako funkcionira, bez razumijevanja zakona poluge. Mislio je pri tome općenito na ono što se u 19 stoljeću nazivalo azijskim načinom mišljenja. Iz toga se u marksističkoj tradiciji razvila teza o ‘azijskom načinu proizvodnje’.

[5] Victor j. Katz i Karen Hunger Parshall u svojoj povijesti algebre (Taming the Unknown, 2014, Princeton University Press) ističu da predavači matematike učenicima ne objašnjavaju da se algebra nije razvila ‘sama od sebe’ nego kao način rješavanja zadataka s kojima su se matematičari praktično suočavali.

[6] Svojih dilema ima i računalno (automatizirano) dokazivanje matematičkih teorema iz aksioma koje se razvija na niz sveučilišta, instituta i u velikim kompanijama (Microsoft). To je jedino važno uočiti i istaknuti, budući da bi članak koji bi ih ovdje pokušao kvalitetno prikazati bio prekompleksan za raspoloživi (misaoni) kapacitet.

[7] Eric Almeida, a Philosophical Examination of Proof in Mathematics, Undergraduate Review, 3, 80-84.

Available at: htp://vc.bridgew.edu/undergrad_rev/vol3/iss1/13

[8] Ovdje se može dodati da su i projekti računalnih automatiziranih dokaza koje sam konzultirao kolektivno djelo, njihova su rješenja ishod diskusije i rezultat izbora puta s neizvjesnostima koje nisu odmah na vidiku, da im je važna preglednost radi uvjerljivosti zaključivanja, i svojevrsne su dijaloške forme, a čak se i sva matematika u nekim od prezentacija tih računalnih sustava opisuje kao sustav pitanja i odgovora.

[9] Zvonimira Šikića (kao i Ivana Fischera) zamolio sam da pročita članak prije objave, da ne iziđe neka glupost. Njegova temeljna primjedba je da razlika između dokaza nekog algoritma kojim se kalkulira zadana vrijednost i zapadnjačkog dokaza (kao u geometriji) – nije razjašnjena, bilo u ovom prikazu ili kod Chemlae. Mogao sam se dakle izvući da razlika nije razjašnjena kod Chemlae, jer je uostalom zaista vrlo tanka, gleda li se apstraktno, mimo matematičke prakse. Tako je Šikić na drugom mjestu opravdano stavio primjedbu da nekako ‘svaki matematički teorem ispada algoritam, npr. Pitagorin jer se operacije primjenjuju na duljine kateta da se dobije duljina hipotenuze. Ne bi li trebalo razlikovati teorem koji se dokazuje od algoritma koji je primjena teorema’ pita Šikić? Nadao sam se da je u članku jasno, nadam se i da sam korektno interpretirao Karine Chemla: Liu Hui dobije zadatak izračuna krnjeg stošca i proceduru kako se izračunava. U komentarima tu proceduru svodi na ono što smatra očitim. To je ono kad matematičari kažu da je izvod trivijalan. Teorem zaista služi kao algoritam, ali teorem se dokazuje iz aksioma, koji bi trebali biti svima neupitni. Liu Hui NE tvrdi da je ono što ističe kao očito – aksiom? Niti je dakle procedura izračuna volumena krnjeg stošca teorem.