Nadigravanje sebičnjaka: Što je zajedničko operi Tosca i prodaji lažne robe za lažni novac

Matematičko modeliranje prikazuje mogući svijet, da je ono što je neočekivano ipak moguće. U seriji (ljetnih) članaka prikazat ćemo različite modele suradnje, pretpostavke, očekivanja i neočekivane ishode. Uvodni članak opisuje poznatu teoriju igara, slučajeve u kojima suradnja ima prednost pred ostvarenjem sebičnog interesa. Svijet suradnje je dakle moguć, no koliko je stvaran, time se model ne bavi

Iako se teorija igara najčešće koristi u ekonomiji, već je odavno našla primjene u mnogim društvenim i prirodnim znanostima. Postala je neka vrsta „kišobrana“ ili „zajedničkog nazivnika“ za ekonomiju, političke znanosti, strateške studije, evolucijsku biologiju, računalne znanosti, socijalnu psihologiju i epistemologiju.

Nastala je davne 1944. godine kada su ekonomist Oscar Morgenstern i matematičar John von Neumann objavili svoju „Teoriju igara i ekonomskog ponašanja“. Samo ime teorije rezultat je opažanja njenih autora da su situacije u kojima se nalaze igrači društvenih igara, poput šaha ili pokera, veoma slične ekonomskim situacijama. U oba slučaja postoje pravila, tj. dopušteni i nedopušteni potezi. Količina informacija dostupna igračima jasno je određena u svakom trenutku. Igrači svoje odluke donose nezavisno. Dobar potez u šahu, pokeru ili poslovnim pregovorima ovisi o očekivanom potezu vašega oponenta. Zato igrači stalno pokušavaju dokučiti što misle njihovi „protivnici“.

John von Neumann i Oscar Morgenstern

Konflikt i suradnja

Zbog tih i mnogih drugih sličnosti, slavni je dvojac krenuo u izgradnju apstraktnog matematičkog modela konflikta (sukoba) i kooperacije (suradnje), koji će omogućiti valjanje procjene očekivanih poteza druge strane u svakoj takvoj situaciji.

(Možda bi bolji naziv teorije bio „interaktivna teorija odlučivanja“, kako predlaže nobelovac Robert Auman, jer se radi o teoriji koja opisuje ponašanja u kojima odluke djeluju jedna na drugu. Kako bilo, teorija igara je opće prihvaćeni termin koji se u dogledno vrijeme sigurno neće mijenjati.)

Dakle, krajnje pojednostavljeno, teorija igara je matematička analiza interaktivnog odlučivanja racionalnih agenata. No, da bi se socijalne interakcije transformirale u modele podložne matematičkoj analizi potrebne su mnoge simplifcirajuće pretpostavke. Prije svega je potrebno da su odluke aktera igre jasno definirane. Osim toga, ishodi odluka se moraju pretvoriti u brojeve. Igrača (kako se obično zovu involvirani akteri) mora biti više i točno se mora znati koji su to igrači. Ishod igre treba biti jednoznačno determiniran odlukama svih igrača. Također se pretpostavlja da su igrači „racionalni“, tj. da razumiju igru i ishode svojih odluka, te da ih donose u svojem „interesu“. Njihov je interes da maksimiziraju svoje isplate, a ne nužno da pobijede svoje protivnike (što je obično slučaj u društvenim igrama i što katkada dovodi do zabune).

Dobro razumijevanje svih tih pretpostavki ključno je za ocjenjivanje valjanosti apstraktne teorije igara u konkretnim situacijama. Na primjer, pretpostavka da su igrači racionalni, da donose logički korektne odluke, otvara pitanje primjenljivosti teorije igara u bilo kojoj stvarnoj situaciji (s akterima koji sigurno nisu logički savršeni). U stvarnim situacijama, osim toga, nije uvijek jasno tko su sve involvirani igrači, što oni žele maksimizirati, što je ishod igre i kako on ovisi o odlukama igrača. Sve su to važna i za primjene nezaobilazna pitanja.

Individualizam

Bez obzira na ova ograničenja apstraktna matematička analiza ipak nudi važne i često iznenađujuće uvide. Na primjer, od Adama Smitha do naših dana ekonomija se temelji na metodološkom individualizmu. Riječ je o stavu da su uzrok svakog socijalnog fenomena individualne motivacije i ponašanja pojedinaca. Dakle, pojedinci su temelj na kojem i iz kojeg moramo graditi razumijevanje ekonomije, politike i društva. Ako u vezi s nekim fenomenom to ne uspijemo, to je samo znak da ga nismo potpuno razumjeli.

(U drugim socijalnim znanostima ekonomiste drže najodanijim sljedbenicima metodološkog individualizma; i sam termin skovao je ekonomist Joseph Schumpeter. Ekonomisti će se s tim sigurno složiti, ako o tome uopće raspravljaju. Razlika je u tome što ekonomisti to smatraju pohvalom, a neekonomisti uvredom.)

Kako bilo, mnogi sumnjaju u metodološki individualizam i čak ga smatraju nečim potpuno nezamislivim. Na primjer, Smithova nevidljiva ruka mnogima je bila (i mnogima još uvijek jest) neprihvatljiva, naprosto zato jer im je nezamislivo „da nitko ne upravlja tom složenom ekonomskom mašinerijom“. Zato je bilo veoma važno da su Arrow i Debreu dokazali teorem  koji, uz pretpostavku tržišne kompeticije te još neke pretpostavke, matematički dokazuje da će pojedinci koji u kompetitivnom tržištu slijede samo svoje vlastite interese, društvo dovesti u optimalno stanje.

Naravno, riječ je o matematičkoj simplifikaciji u kojoj su termini „vlastiti interes“, „optimalno stanje“, „kompetitivno tržište“ itd. tehnički termini matematičke ekonomije, koje ne treba iščitavati kolokvijalno (pa npr. tim teoremom opravdavati laissez-faire politike). Ono što su Arrow i Debreu dokazali jest da je „nevidljiva ruka“ moguća u jednom simplificiranom matematičkom modelu (koji je jako daleko od stvarnosti, usp. „O matematičkoj neumitnosti tržišnih zakona“, Poučak br. 50.).

Ako je „nevidljiva ruka“ moguća u njihovom simplificiranom modelu, onda postaje zamislivo da nešto slično vrijedi i u stvarnim bitno složenijim situacijama. Njihovim je teoremom odbačena jedna ogromna predrasuda, koja je proizlazila iz nedostatka imaginacije. „Ne mogu to zamisliti, dakle toga nema.“ Nakon njihovog matematičkog dokaza svi to možemo zamisliti i time smo oslobađeni jednog uskog vidokruga.

Teorija igara također nam daje takve uvide. Vidjet ćemo kako jedna veoma simplificirana igra (zatvorenikova dilema) pokazuje da slijediti vlastiti interes nije nužno dobra strategija za ostvarenje vlastitih interesa. Time se ruši još jedna predrasuda tipa „ne mogu to zamisliti, dakle toga nema“.

(Sličnu ulogu, u suzbijanju predrasuda o evoluciji, ima Conwayeva igra „Game of life“. Mnogi ljudi ne mogu zamisliti da nevjerojatno složene životne forme nastaju iz bitno jednostavnijih formi. Conwayeva igra pokazuje kako je to moguće, u jednom simplificiranom slučaju. Njegove individue su kvadratići na beskonačnoj šahovskoj ploči, koji se „rađaju“, „žive“ i „umiru“ ovisno o tome koliko je „živih“ kvadratića među njihovih 8 susjeda. Ako su točno 2 susjeda živa, kvadratić ostaje u stanju u kojem je, ako su 3 susjeda „živa“ i on „oživi“, a u svim ostalim slučajevima „umire“. Iz ove super jednostavne forme „rađanja“ i „umiranja“ nastaju, mnogima ranije nezamislivo, forme koje se gibaju, hrane, reproduciraju, i čak igraju šah. Možete se i sami poigrati ako u svoju tražilicu upišete „Game of life“.)

Uloga matematike i njenih teorema u socijalnim znanostima najčešće je toga tipa. Takva je stoga i uloga teorije igara. Njeni modeli uvijek su simplificirani i ne mogu se direktno primijeniti na realni svijet (kao što se mogu na simplificirane i zapravo fundamentalne uvjete prirodno-znanstvenih laboratorija).

Ali matematički rezultati (o njenim simplificiranim modelima) zato mogu jasno pokazati da su neke, na prvi pogled, nezamislive ideje ipak zamislive, pa možda čak i realne.

Dakle, matematički rezultati teorije igara mogu nam pomoći da stvarnost počnemo gledati na novi način koji nudi jučer nezamisliva, a danas možda istinita rješenja. 

Zatvorenikova dilema

Neke osnovne ideje teorije igara ilustrirat ćemo na slavnoj igri Flooda i Dreschera iz 1950. godine. Ona će nam štošta reći o mogućnosti i nemogućnosti suradnje. Zatvorenikovom dilemom nazvao ju je A. Tucker (koji je o njoj objavio prvi članak 1951. godine) budući da ju je predstavio u obliku kratke priče o dva zatvorenika.

Policija je pritvorila dva osumnjičenika koje tereti za teško kriminalno djelo. Za to teško djelo tužitelj nema valjanih dokaza, ali ih ima za jedno lakše. Zato obojici, i to svakome posebno, nudi sljedeće: 

„Ako priznaš da ste počinili teže djelo ti ćeš biti oslobođen, a tvoj će suučesnik dobiti 10 godina zatvora. Ta ponuda vrijedi samo ako tvoj suučesnik ne prizna. Naime, ako oba priznate dobit ćete svaki po 5 godina. Ako ni jedan od vas ne prizna dobit ćete po 1 godinu za lakše djelo, za koje imam dokaze.“

Situacija u kojoj se nalaze dva zatvorenika može se sažeti u sljedeću tablicu.

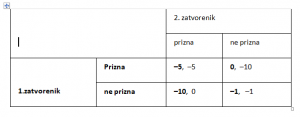
Prvi (masno otisnuti) broj u svakoj ćeliji pokazuje što dobiva 1. zatvorenik, dok drugi broj opisuje što dobiva 2. zatvorenik. Brojevi predstavljaju godine izgubljene u zatvoru i zato su negativni. Dakle, najbolji rezultat je 0, a najlošiji –10.

Igra pretpostavlja da zatvorenici ne mare jedan za drugoga. Brine ih samo vlastiti interes koji je što manje godina provedenih u zatvoru. Što će učiniti? Vjerojatno će oba rezonirati na sljedeći način:

„Ako moj suučesnik prizna, moje su alternative: priznati i dobiti 5 godina zatvora ili ne priznati i dobiti 10 godina zatvora. Očito mi je bolje priznati. Ako pak moj suučesnik ne prizna, moje su alternative: priznati i biti oslobođen ili ne priznati i dobiti 1 godinu zatvora. Očito mi je i tada bolje priznati. Sve u svemu, što god učinio moj suučesnik meni je bolje priznati.“

Slijedeći svoje interese oba će zatvorenika priznati i u zatvoru provesti dugih 5 godina. Da ni jedan nije priznao u zatvoru bi proveli samo 1 godinu.

Paradoks zatvorenikove dileme jest da slijeđenje vlastitih interesa radi protiv samih tih interesa, tj. dovodi do 5 umjesto 1 zatvorske godine. Jednostavna logička argumentacija definitivno odbacuje kooperativno ponašanje zatvorenika – njihovo obostrano nepriznavanje u dilemi u kojoj se nalaze. (Taj se jednostavni argument naziva „principom dominacije“ : ako je opcija A za vas bolja od opcije B, bez obzira što čine drugi igrači, onda se kaže da A „dominira“ B i u takvoj situaciji trebate učiniti A. Naravno, u slučaju zatvorenikove dileme, A je „priznati“ a B „ne priznati“.)

Možda je moguć svijet u kojem nema zatvorenikovih dilema (vidjet ćemo uskoro koji mehanizmi mogu stvoriti takav svijet), no naš svijet, ovakav kakav jest, prepun je tih dilema. Evo još nekoliko primjera.

Dva trgovca, jedan preko puta drugog, prodaju isti proizvod čiju cijenu moraju oglasiti početkom svakoga tjedna (i ne smiju je mijenjati u tom tjednu). Obojica razmišljaju na sljedeći način: „Kada bih drugog trgovca izbacio iz posla moja bi se zarada udvostručila. Možda bih zato trebao sniziti svoju cijenu i tako kupce privući sebi, a odvući ih od konkurencije.“

Potaknuti ovom idejom obavili su proračune i zaključili da će snižavanjem cijene povećati svoj profit s 1 na 4 obračunske jedinice, pod uvjetom da drugi trgovac zadrži svoju cijenu. On će tada biti na gubitku 3 obračunske jedinice i to će ga vjerojatno izbaciti iz posla. Ako (vođeni ovakvim razmišljanjem) oba trgovca snize cijenu profit obojice past će na 0 obračunskih jedinica, što će ugroziti oba posla. Sve to opet možemo sažeti u jednostavnu tablicu:

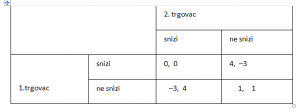
Dilema trgovaca identična je dilemi zatvorenika. Što god učinio jedan trgovac, drugome je bolje da snizi svoju cijenu. (Ako drugi trgovac snizi svoju cijenu i prvome je bolje da je snizi, jer je 0 bolje od –3. Ako pak drugi trgovac ne snizi svoju cijenu, prvome je opet bolje da je snizi, jer je 4 bolje od 1. Prema principu dominacije prvi trgovac treba sniziti cijenu. Naravno, isto vrijedi i za drugog trgovca.)

Slijedeći svoje želje za većim profitom oba će trgovca sniziti svoje cijene i ostati bez profita. Da nisu snizili svoje cijene ostao bi im stari profit od 1 obračunske jedinice.

Čak i obična kupnja i prodaja mogu dovesti do zatvorenikove dileme. Na crnom tržištu, gdje se kupac i prodavač susreću samo jednom i gdje nema vremena za provjeru robe i novca, to je uobičajena pojava. Ja možda kupujem bezvrijednim lažnim novcem, a vi mi možda prodajete bezvrijednu lažnu robu. Nakon što smo brzo obavili transakciju i još se brže rastali, moj najbolji ishod je zarada od 500 kuna (koliko meni vrijedi roba koju želim kupiti) i koju ostvarujem tako da vam robu (koja vama vrijedi 300 kuna, a za koju tražite 400) platim s 400 lažnih kuna. Naravno vi ste time izgubili 300 kuna.

Vaš najbolji ishod je prodaja bezvrijedne lažne robe za mojih 400 pravih kuna. Sada vi dobivate a ja gubim 400 kuna. Kupim li vašu bezvrijednu lažnu robu mojim bezvrijednim lažnim novčanicama, nitko nije ništa zaradio ni izgubio. Kupim li vašu valjanu robu mojim valjanim novčanicama, oboje smo zaradili po 100 kuna (jer sam ja za 400 kuna dobio nešto što mi vrijedi 500 kuna, a vi ste za nešto što vam vrijedi 300 kuna dobili 400 kuna). Evo i tablice u kojoj sve to možete lakše pratiti.

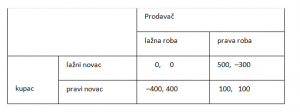
Lako vidimo da je opet riječ o zatvorenikovoj dilemi. Princip dominacije i kupca i prodavača vodi prema konfliktnom ishodu (0, 0) koji je opet lošiji od kooperativnog ishoda (100, 100).

Tosca

Zatvorenikovu dilemu nalazimo i u Puccinijevoj Tosci. Korumpirani Scarpia osudio je Toscinog ljubavnika Caravadossija na smrt, ali ga je spreman pomilovati za Toscinu ljubav. Ako mu se Tosca poda streljački će vod u Caravadossija pucati ćorcima. Tosca je nepovjerljiva i pristaje spavati s Scarpiom tek ako pošalje pisanu i neopozivu naredbu da se u puške streljačkog voda stave ćorci.

Spasonosna naredba poslana je pred Toscinim očima, no ona ipak nije kooperativna. Scarpiu prima u smrtonosni zagrljaj. Ubija ga i juri na Sant Angelo gdje je čeka voljeni koji „pogođen“ čorcima treba odglumiti svoju smrt.

No, ni Scarpia nije bio kooperativan. Naredba je bila lažna. Cavaradossi je stvarno pogubljen, a Tosca se kada to shvati baca sa Sant Angela kako bi se sa svojim voljenim sjedinila u smrti. Sve uz nezaboravne arije.

(Neću profanirati ovu bezvremenu priču prizemnom tablicom. Možete je i sami ispisati, te se tako uvjeriti kako se i tu radi o zatvorenikovoj dilemi.)

Zatvorenikova dilema je dilema između sukoba i suradnje u situacijama u kojima je suradnja očito potrebna, ali i teško ostvariva. Slijediti vlastiti interes nije nužno dobra strategija za ostvarenje vlastitih interesa

Logika utrke u naoružanju također je logika zatvorenikove dileme. Ravnoteža između supersila može se postići tako da se one obje naoružaju „do zuba“ ili da se obje naoružaju umjereno. Jeftinija ravnoteža, koja se postiže umjerenim naoružavanjem,  za obje je supersile bolja opcija. No,  njihova će trka ipak završiti u ravnoteži ogromnih arsenala.

Naime, tablica sada izgleda ovako:

Brojevi određuju redoslijed preferencija pojedinih ishoda za obje strane (veći broj preferiran je manjem; dakle 3 je bolje od 2 itd.). Umjerena ravnoteža (3, 3) bolja je od skupe ravnoteže (2, 2). Naravno, prvoj je supersili najbolje biti jako naoružanom, ako je njen protivnik slabo naoružan (to odgovara ishodu (4, 1)). Najgore joj je biti slabo naoružanom, ako je njen protivnik jako naoružan (to odgovara ishodu (1, 4)). Isto vrijedi i za drugu super  silu. Princip dominacije, opet će natjerati naše supersile da završe u lošijoj, skupoj i opasnijoj ravnoteži (2, 2) a ne u boljoj, jeftinijoj i manje opasnoj (3, 3).

Nakon svih ovih primjera možemo zaključiti da je zatvorenikova dilema dilema između sukoba i suradnje u situacijama u kojima je suradnja očito potrebna, ali i teško ostvariva. U našim primjerima: zatvorenici bi trebali međusobno surađivani ne priznavajući, trgovci bi trebali surađivati ne snižavajući svoje cijene, kupac i prodavač trebali bi surađivati a ne varati jedan drugoga, kao i Tosca i Scarpia, a super sile bi trebale surađivati ne naoružavajući se „do zuba“. Nažalost, besprijekorna logika principa dominacije neizbježno ih vodi u sukob koji završava lošijim ishodima.

Analiziramo li sve ove primjere ustanovit ćemo da do zatvorenikove dileme uvijek vodi ista formula: iskušenje da se konfliktnim ponašanjem ostvari dobit na račun kooperativnog ponašanja, plus garantirano lošiji ishod ako svi igrači podlegnu tom iskušenju.

Toga su tipa i zatvorenikove dileme s više od dva igrača. Na primjer, ako svi seljaci za ispašu koriste zajednički pašnjak onda je svaki od njih u iskušenju da ga koristi nešto više od drugih i tako bolje nahrani svoje stado. Međutim, učine li to svi seljaci pašnjak će biti uništen, pa na kraju od njega nitko neće imati koristi. Slične bismo priče mogli ispričati o izlovu ribe ili korištenju nekog drugog javnog resursa. Takve se situacije, iz očitoga razloga, zovu „tragedijama javnoga dobra“ i one su daljnji primjeri zatvorenikove dileme.

Primijetimo da bi se ponašanje igrača možda moglo promijeniti ako bi isti igrači igru igrali više puta (ako sam vam jednom platio lažnim novcem, drugi ćete put biti oprezniji). Koja je logika optimalnog igranja tako iterirane zatvorenikove dileme, vidjet ćemo u sljedećem odjeljku.

U sljedećem članku:

Reciprocitet kao izvor kooperacije