Proširena logika vjerojatnosti. Počeci i suvremeni kontekst

Logika počiva na binarnim propozicijama - one mogu biti istinite ili lažne. U 6. članku o vjerojatnosti, Zvonimir Šikić pokazuje kako se vjerojatnost može promatrati kao proširena propozicijska logika, u kojoj propozicije mogu biti više ili manje vjerojatne, a u drugom dijelu teksta demonstrira generalizaciju propozicijskih formula.

• Naslovna fotografija: Britanski matematičar, filozof i logičar George Boole (Creative Commons)

• Prethodni članci: Očekivanje u vjerojatnosti. Petrogradski paradoks i problem dvije omotnice, Kako je manje ispravna metoda zamijenila puno ispravniju. Laplace vs. Fisher, Klasična vjerojatnost i primjeri povijesnog razvoja, Vjerojatnost kao frekvencija, Vjerojatnost kao stupanj plauzibilnosti. Matematički temelji bejesovske teorije

Temeljna ideja da je teorija vjerojatnosti zapravo logika koja uzima u obzir da propozicije nisu nužno istinite ili lažne, nego mogu biti manje ili više vjerojatne, potiče još od Georgea Boolea. Vidjeli smo da su je pokušali revitalizirati Keynes i Jeffreys, ali u tome nisu uspjeli pa je pala u zaborav. Primjene je preuzela Fisherova frekvencijska statistika, a teoriju Kolmogorovljeva matematička teorija vjerojatnosti. Revitalizirao ju je Hailperin 1996. smjestivši vjerojatnost u kontekst suvremene matematičke logike.

Tekst koji slijedi teže će pratiti oni koji ne znaju bar nešto formalne logike, ali vjerujem da će i oni steći osnovni dojam da je teorija vjerojatnosti prirodni nastavak logike, a to je i jedini cilj ovoga članka.

• Istinitost i vjerojatnost

Klasična bivalentna logika pretpostavlja da su propozicije svih jezika kojima se bavi istinite ili neistinite. Ako funkciju koja rečenicama pridružuje njihove vrijednosti istinitosti označimo s V (veritas), a vrijednosti istina i neistina s 1 i 0, imamo sljedeću definiciju istinitosti za propozicijsku logiku istinosno-funkcionalnih veznika (možemo se ograničiti na veznike ∨ (ili),  ∧ (i) , – (ne), jer se svi drugi mogu definirati pomoću ta tri).

Definicija istinitosti

Funkcija istinitosti V je svaka funkcija sa skupa {∨, ∧, -}-formula u skup {0, 1}, koja zadovoljava sljedeća pravila:

\(\text{(V1)} \quad V(-A) = 1 – V(A) \\­ \\ \text{(V2)} \quad V(A \vee B) = \max\{V(A), V(B)\} \\ ­ \\ \text{(V3)} \quad V(A \wedge B) = \min\{V(A), V(B)\} \)

Često ne znamo je li neka propozicija istinita ili neistinita, nego tek da je manje ili više vjerojatna. Ono što znamo jest da tautologije trebaju imati maksimalnu vjerojatnost 1, kontradikcije minimalnu vjerojatnost 0 te da je vjerojatnost aditivna na propozicijama koje se isključuju. Zato funkciju koja propozicijama pridaje njihove vjerojatnosti, a koju označavamo s Pr (probabilitas), definiramo na sljedeći način.

Definicija vjerojatnosti 

Funkcija vjerojatnosti Pr je svaka funkcija definirana na skupu {∨,  ∧, -}-formula, koja zadovoljava sljedeća pravila:

\( \text{(P0)} \quad \Pr (A) \in [0,1] \\ ­ \\ \text{(P1)} \quad A \text{ je tautologija } \Rightarrow \Pr (A) = 1 \quad A \text{ je kontradikcija } \Rightarrow \Pr (A) = 0 \\ ­ \\ \text{(P2$\vee$)} \quad A \text{ i } B \text{ se isključuju } \Rightarrow \Pr (A \vee B) = \Pr (A) + \Pr (B) \)

Lako je dokazati da iz tih pravila slijede sljedeća pravila:

\(
\text{(P1′)} \quad \Pr (A) + \Pr (-A) = 1 \\ ­ \\
\text{(P2’$\vee$)} \quad \Pr (AB) + \Pr (A \vee B) = \Pr (A) + \Pr (B) \\ ­ \\
\text{(P3)} \quad \text{Iz } A \text{ slijedi } B \Rightarrow \Pr (A) \leq \Pr (B) \quad A \text{ je ekvivalentno } B \Rightarrow \Pr (A) = \Pr (B)
\)

Dokaz od (P1′) je trivijalan:      \(\small 1 = \Pr (A \vee \overline{A}) = \Pr (A) + \Pr (\overline{A}).\)

Dokaz pravila (P3) također je lagan:

\(
\text{Iz } A \text{ slijedi } B \Rightarrow A \text{ i } -B \text{ se isključuju } \Rightarrow 1 \geq \Pr (A \vee \overline{B}) = \Pr (A) + \Pr (\overline{B}) = \Pr (A) + 1 – \Pr (B).
\)

Drugi dio od (P3) očito slijedi iz prvoga.

Pravilo (P2’∨), uz standardnu pokratu AB za A∧B, slijedi iz:

\(
\Pr (A \vee B) = \Pr (A \vee \overline{A}B) = \Pr (A) + \Pr (\overline{A}B) \quad \text{i} \quad \Pr (B) = \Pr (AB \vee \overline{A}B) = \Pr (AB) + \Pr (\overline{A}B).
\)

Ako „rizik od A“ definiramo kao R (A) = Pr (-A), lako dokazujemo i dualna pravila (jer su obična preformulacija izvornih pravila):

\(
\text{(R0)} \quad R (A) \in [0,1] \\­ \\
\text{(R1)} \quad A \text{ je tautologija } \Rightarrow R (A) = 0 \quad A \text{ je kontradikcija } \Rightarrow R (A) = 1 \\­ \\
\text{(R1′)} \quad R (A) + R (-A) = 1 \\ ­\\
\text{(R2$\wedge$)} \quad A \text{ i } B \text{ se isključuju } \Rightarrow R (A \wedge B) = R (A) + R (B) \\ ­ \\
\text{(R2’$\wedge$)} \quad R (AB) + R (A \vee B) = R (A) + R (B) \\ ­ \\
\text{(R3)} \quad \text{Iz } A \text{ slijedi } B \Rightarrow R (A) \geq R (B) \quad A \text{ je ekvivalentno } B \Rightarrow R (A) = R (B)
\)

Ekvivalentnosti od (P0) i (R0), (P1) i (R1), (P2 ∨) i  (R2 ∧), (P2′ ∨) i (R2′ ∧) te (P3) i (R3) slijede neposredno iz definicije od R i činjenice da su valjanost od A i kontradiktornosti od -A  ekvivalentne te da A slijedi iz B ako i samo ako –B slijedi iz -A.

Pravilo (R3)  lako je generalizirati do sljedećeg teorema.

Teorem o zbroju rizika

\(\small \text{Iz } A_{1}, A_{2}, \ldots , A_{n} \text{ slijedi } B \Rightarrow R (A_{1}) + R (A_{2}) + \ldots + R (A_{n}) \geq R (B) \)

Da vjerojatnost Pr poopćava istinitost V iskazuje sljedeći teorem.

Teorem o vezi istinitosti i vjerojatnosti

Svaka funkcija istinitosti je funkcija vjerojatnosti. S druge strane, ako funkcija vjerojatnosti prima samo vrijednosti 0 i 1 onda je ona funkcija istinitosti.

Za dokaz prve tvrdnje, najprije uočimo da V trivijalno zadovoljava (P0) i (P1). Nadalje, vidimo da zadovoljava i (P2) jer je

\(\small V (A \vee B) + V (AB) = \max \{V (A), V (B)\} + \min \{V (A), V (B)\} = V (A) + V (B)\)
,

a za A i B koji se logički isključuju vrijedi V (AB) = 0.

Za dokaz druge tvrdnje, uočimo da iz AB slijedi A∨B pa vrijedi Pr (AB) ≤ Pr (A ∨ B). Zato iz

\(\small \Pr (A) + \Pr (B) = \Pr (AB) + \Pr (A \vee B)\)

slijedi da Pr (AB) i Pr (A ∨ B) moraju imati sljedeće vrijednosti iz {0, 1}, kada Pr (A) i Pr (B) imaju vrijednosti iz {0, 1}:

Pr (A)	Pr (B)	Pr (AB)	Pr (A∨B)
0	0	0	0
0	1	0	1
1	0	0	1
1	1	1	1

Dakle, Pr (A ∨ B) = max { Pr (A), Pr (B)} i Pr (A ∧ B) = min { Pr (A), Pr (B)}, što smo i trebali dokazati.

• Istina u V-modelu i vjerojatnost u P-modelu

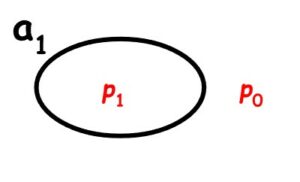
Model ili interpretacija formalnog jezika propozicijske logike je funkcija V₀ koja svakoj atomarnoj formuli toga jezika pridružuje vrijednosti istinitosti 0 ili 1. Istinitost u toj interpretaciji tada je funkcija V koja se na sve formule toga jezika proširuje prema prethodnim pravilima za definiciju istinitosti. Svaki V₀  jednoznačno određuje V i svaki V jednoznačno određuje V₀ pa ćemo ih često identificirati.

Ako atomarnih formula ima konačno mnogo onda je odabir modela V₀ ekvivalentan odabiru jednog konjunktivnog bloka tih atomarnih formula, tj. ekvivalentan  je pridruženju vrijednosti 1 tom bloku i vrijednosti 0 svim drugim blokovima. Na primjer, u slučaju dva atoma a₁ i a₂, odabir modela V₀ (a₁) = 1, V₀ (a₂) = 0 ekvivalentan je odabiru bloka \(a_{1}\overline{a_{2}}\), tj. ekvivalentan je pridruženju vrijednosti 1 bloku \(a_{1}\overline{a_{2}}\), i vrijednosti 0 blokovima \(a_{1}a_{2}\), \(\overline{a_{1}}a_{2}\), \(\overline{a_{1}}\overline{a_{2}}\). Grafički prikaz tog modela je

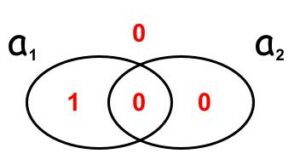
Konjunktivne blokove izgrađene od atoma zvati ćemo konstituentima, kako ih je zvao Boole, ili ćelijama (u skladu s njihovim grafičkim prikazom). Dakle, sljedeća definicija modela (interpretacije) ekvivalentna je prethodnoj.

Definicija V-modela

V-model za formalni jezik propozicijske logike koji je izgrađen nad atomima a₁ , … , a_n jest funkcija V sa skupa njihovih konstituenti {C₁, … , C₂ⁿ} u skup {0, 1}, koja prima vrijednost 1 na točno jednom konstituentu i vrijednost 0 na svima ostalima. Za takvu funkcija vrijedi:

\(\sum_{1}^{2^n} V(C_i) = \sum_{1}^{2^n} v_i = 1\).

Računanje vrijednosti istinitosti proizvoljne formule, u V-modelu zadanom gornjim grafom, ilustriramo na primjeru formule \(a_{1} \rightarrow a_{2}\) . Njena potpuna alternacijska forma je \(\small{ a_1 a_2 \lor \overline{a_1} a_2 \lor \overline{a_1} \overline{a_2}} \)  pa je

\(
V(a_{1} \rightarrow a_{2}) = V(a_{1} a_{2}) + V(\overline{a_{1}} a_{2}) + V(\overline{a_{1}} \overline{a_{2}}) = 0 + 0 + 0 = 0
\)
.

Formula \( a_{1} \rightarrow a_{2} \) u tom je modelu neistinita.

Općenito imamo sljedeću definiciju koja je ekvivalentna standardnoj.

Definicija istinitosti u V-modelu

Formula A jezika propozicijske logike izgrađena nad atomima \( a_{1}, \ldots, a_{n} \) u modelu V ima vrijednost istinitosti

\( V(A) = \sum_{A} V(C_{i}) = \sum_{A} v_{i}, \)

gdje se sumira po svim konstituentima C_i koje čine potpunu alternacijsku formu od A.

Definicija Pr-modela poopćena je definicija V-modela.

Definicija Pr-modela

Pr-model za formalni jezik propozicijske logike izgrađen nad atomima \( a_{1}, \ldots, a_{n} \)  jest funkcija Pr sa skupa njihovih konstituenti {C₁, … , C₂ⁿ} u interval [0,1], za koju vrijedi

\( \sum_{i=1}^{2^n} Pr(C_i) = \sum_{i=1}^{2^n} p_i = 1 \).

Grafički prikaz jednog takvog  Pr-modela za jezik propozicijske logike izgrađen nad atomima a₁, a₂ jest

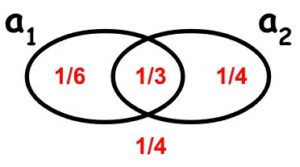
Računanje vjerojatnosti proizvoljne formule u P-modelu koji je zadan gornjim grafom ilustriramo na primjeru formule \(\small a_{1} \rightarrow a_{2} \). Njena potpuna alternacijska forma je \(\small a_{1}a_{2} \vee \overline{a_{1}}a_{2} \vee \overline{a_{1}}\overline{a_{2}} \)  pa je

\( \Pr(a_{1} \rightarrow a_{2}) = \Pr(a_{1} a_{2}) + \Pr(\overline{a_{1}} a_{2}) + \Pr(\overline{a_{1}} \overline{a_{2}}) = \frac{1}{3} + \frac{1}{4} + \frac{1}{4} = \frac{5}{6} \)

Formula \(\small a_{1} \rightarrow a_{2} \) u tom modelu ima vjerojatnost 5/6.  Općenito imamo sljedeću definiciju.

Definicija vjerojatnosti u Pr-modelu

Formula A jezika propozicijske logike izgrađena nad atomima \( a_{1}, \ldots, a_{n} \) u modelu Pr ima vjerojatnost

\( \Pr(A) = \sum_{A} \Pr(C_{i}) = \sum_{A} p_{i} \),

gdje se sumira po svim konstituentima C_i koji čine potpunu alternacijsku formu od A.

Dakle, V-model i istinitost u V-modelu posebni su slučajevi Pr-modela i vjerojatnosti u Pr-modelu, u kojem su vrijednosti \(\small p_{i} \in \{0, 1\} \).

Kada su Fermat, Pascal, Bernoulli, Bayes, Laplace, De Morgan, Boole, Jeffreys ili Keynes govorili o vjerojatnosti, oni su govorili o vjerojatnosti propozicija (kao i mi u ovom poglavlju). No, današnja matematička teorija vjerojatnosti govori o vjerojatnosti događaja koje shvaća kao podskupove skupa elementarnih ishoda nekog slučajnog eksperimenta. Tu je praksu etablirao Kolmogorov koji je 1933. formulirao zadovoljavajuću teoriju stohastičkih situacija u kojima se pojavljuje beskonačno mnogo elementarnih ishoda. Radilo se o aksiomatizaciji vjerojatnosti kao normalizirane mjere na algebri skupova. U konačnom slučaju imamo sljedeću definiciju (usp. 1. članak „Klasična vjerojatnost“).

Definicija konačnog prostora vjerojatnosti

Konačni prostor vjerojatnosti je par (Ω, Pr), gdje je Ω konačni neprazni skup (čiji elemente zovemo  elementarnim slučajnim događajima, a njegove podskupove slučajnim događajima), dok je Pr funkcija sa skupa svih podskupova od Ω u [0,1], za koju vrijede sljedeći aksiomi:

I. \(\small \Pr(\Omega) = 1.\)

II. \(\small \Pr(A \cup B) = \Pr(A) + \Pr(B).\)

za sve A i B koji su podskupovi od Ω i koji se međusobno isključuju.

Konačni prostor vjerojatnosti modelira stohastičke situacije u kojima eksperiment uvijek rezultira točno jednim od mogućih ishoda w_i, …, w_n, a kojim će od njih rezultirati stvar je slučaja. Tada je Ω  = { w_i, …, w_n }. Vrijednost Pr (w_i) jednaka je vjerojatnosti da ishod eksperimenta bude w_i, a vjerojatnost Pr nekog događaja A je

\(\Pr(A) = \sum_{A} \Pr(w_{i}) = \sum_{A} p_{i}\) ,

gdje se sumira po svim w_i ∈ A (suma je 0 za A = ∅).

Svakom konačnom prostoru vjerojatnosti možemo pridružiti ekvivalentni P-model, ako o a_i mislimo kao o propoziciji „desio se w_i“, za konstituent \( \small C_{i} = \overline{a_1}, \ldots, \overline{a_{i-1}}, a_{i}, \overline{a_{i+1}}, \ldots, \overline{a_{n}}\) definiramo \(\small{ \Pr(C_i) \mathrel{:=} \Pr(w_i)} \), a za one koji nisu tog oblika definiramo \(\small{ \Pr(C_{j}) \mathrel{:=}  0}\). Tako definirani P-model očito je ekvivalentan početnom prostoru vjerojatnosti.

Obratno, iz svakog konačnog P-modela možemo izgraditi ekvivalentni konačni prostor vjerojatnosti. Njegovi elementarni ishodi w_i su oni konstituenti C_i čija je vjerojatnost veća od nule. Vjerojatnost Pr na njima definiramo sa \(\small \Pr(w_{i}) \mathrel{:=} \Pr(C_{i})\), što se, po II. pravilu, aditivno proširuje na sve skupove elementarnih ishoda.

Dakle, ne samo da je istina posebni slučaj vjerojatnosti (što smo dokazali teoremom o istini i vjerojatnosti) nego je i svaki veristički model propozicijskih formula posebni slučaj probabilističkog modela propozicijskih formula.

Isto vrijedi za verističku i probabilističku implikaciju.

• Veristička i probabilistička implikacija

Pojam implikacije standardno se definira na sljedeći način.

\( A_1, A_2, \ldots, A_m \models B \quad \text{akko} \quad \left(\forall V \right) \left( \left( \forall i \right)  V(A_i) \right) = 1 \Rightarrow V(B) = 1  \) .

Riječima, propozicije A₁, A₁, … , A_m impliciraju propoziciju B ako je u svakoj interpretaciji V u kojoj su sve A_i istinite i B istinita.

Evo i naizgled općenitije definicije.

Definicija verističke implikacije

\(\small V (A_1) \in \alpha_1, \ldots, V (A_m) \in \alpha_m \models V (B) \in \beta \text{ akko } (\forall V) ( (\forall i) V (A_i) \in \alpha_i \Rightarrow V (B) \in \beta)\),

gdje su \(\small \alpha_i, \beta\) neprazni intervali \(\small \subseteq \lbrace 0,1 \rbrace \).

Zaista se radi samo o naizgled općenitijoj definiciji, jer V (X) ∈ {0} uvijek možemo zamijeniti sa V (-X) = 1, dok je V (X) ∈ {0, 1} kao pretpostavka nepotrebna, a kao konkluzija je trivijalna. Definicija probabilističke implikacije poopćenje je verističke.

Definicija probabilističke implikacije

\( \small Pr (A_1) \in \alpha_1, \ldots, Pr (A_m) \in \alpha_m \models Pr (B) \in \beta \text{ akko } (\forall Pr) ( (\forall i) Pr (A_i) \in \alpha_i \Rightarrow Pr (B) \in \beta) \),

gdje su \(\small \alpha_i, \beta\) neprazni intervali \(\small \subseteq [0,1] \).

Veristička implikacija očito je posebni slučaj probabilističke implikacije u kojoj su vrijednosti od Pr iz {0, 1}.

Razmotrimo, na primjer, probabilističku verziju modus ponensa:

\( {\small Pr (A) = p, Pr (A \rightarrow B) = q \models Pr (B) \in \beta} \).

Ta implikacija trivijalno vrijedi za β = [0,1]. Problem je naći optimalni β koji će modus ponens činiti valjanim u svakom modelu zadanom s p₁, p₂, p₃ i p₄:

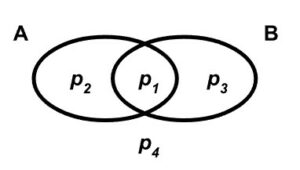
Može se dokazati da je optimalni interval β = [p + q – 1, q] pa je probabilistički optimalni modus ponens:

\( {\small Pr (A) = p, Pr (A \rightarrow B) = q \models Pr (B) \in [p + q – 1, q]} \).

Možemo ga zapisati i u sljedećem obliku:

\( {\small R (A) = p, Pr (A \rightarrow B) = q \models Pr (B) \in [q – p, q]} \).

(Za one koji znaju odgovarajuću srednjoškolsku matematiku nudimo i dokaz da je baš taj interval optimalan. Dakle, trebamo odrediti minimum i maksimum funkcije w = p₁ + p₃ uz ograničenja (1):

p₁ + p₂  = p

p₁ + p₃  + p₄ = q

p₁+ p₂  + p₃  + p₄ = 1

p₁, p₂, p₃, p₄ ≥ 0

Lako nalazimo da iz (1) slijedi (2):

p₁ = p + q – 1 ≥ 0

p₂ = 1 – q ≥ 0

p₃ = 1 – p – p₄ ≥ 0

p₄ ≥ 0

Iz (2) odmah slijedi da su p + q  ≥ 1, q ≤ 1 i p ≤ 1 nužni uvjeti da bi problem imao rješenje. Funkcija w = p₁ + p₃  prima minimalnu i maksimalnu vrijednost u vrhovima nepraznog, omeđenog i konveksnog poliedra koji je zadan sustavom (1), a sve su njene vrijednosti u intervalu [min w, max w]. Određenje tog minimuma i maksimuma jest problem linearnog programiranja. U našem jednostavnom slučaju, sustavu (1) dodajemo p₁ + p₃  = w te eliminiramo sve varijable osim w pa iz (2) lako nalazimo

w = q – p₄,      p + q —1 < w < q.

To smo i trebali dokazati.)

Na sličan način možemo dokazati da, na primjer, vrijede i sljedeće probabilističke implikacije.

Pr (A) = p, Pr (B) = q   ⊨   Pr (A ∨ B) ∈[max{p, q}, p + q]

R (A) = p, R (B) = q    ⊨    R (AB) ∈[max{p, q}, p + q]

R (A → B) = p, R (-A → B) = q   ⊨   R (B) = p + q

Pr (A → B) = p   ⊨   Pr (B → A) ∈ [1 – p, 1]

R (A) ∈[0, p],  R (A → B) ∈[0, p]    ⊨   R (B) ∈[0, 2p]

Dobro je poznato da je veristička propozicijska implikacija odlučiva pomoću istinosnih tablica i mnogih drugih testova. Hailperin je 1996. dokazao da je odlučiva i probabilistička propozicijska implikacija.

Teorem o odlučivosti probabilističke propozicijske implikacije

Svaka probabilistička implikacija, Pr (A₁) ∈ α₁, … , Pr (A_m) ∈ α_m ⊨  Pr (B) ∈ β, gdje su A_i i B formule propozicijske logike, odlučiva je za neprazne intervale α_i,β ⊆ [0,1] čiji su krajevi racionalni brojevi. Odlučivo je i je li  β optimalan.

Dokaz koji prelazi okvire ovoga teksta, zapravo je dokaz da metoda linearnog programiranja uvijek dovodi do odluke.

• Uvjetne vjerojatnosti i implikacija među njima

Uvjetnu vjerojatnost Pr (B|A), tj. vjerojatnost od A, ako jest B, definiramo na uobičajeni način.

Definicija uvjetne vjerojatnosti

Ako je Pr (A) ≠ 0 onda je

\( Pr(B | A)= \frac{Pr(AB)}{Pr(A)} = \frac{\sum_{AB} Pr(C_i)}{\sum_{A} Pr(C_i)} \)

gdje se sumira po svim konstituentima C_i koji čine potpunu alternacijsku formu od AB odnosno A.

Uočimo da je Pr (B|A) ≠ Pr (A∘B) za svaki propozicijski veznik ∘. Naime, Pr (B|A) je linearna razlomljena forma dok je Pr (A∘B) uvijek linearna forma od Pr (C_i) s koeficijentima iz {0, 1}. Posebno, Pr (B|A) ≠ Pr (A→B). U tom slučaju možemo dokazati i više. Naime,

\( Pr (A \rightarrow B) = Pr(- (A\overline{B})) = 1 – Pr(A\overline{B}) \)

\( Pr(B | A) = \frac{Pr(AB)}{Pr(A)} = \frac{Pr(A) – Pr(A\overline{B})}{Pr(A)} = 1 – \frac{Pr(A\overline{B})}{Pr(A)}\)

Sve u svemu, \( {\small Pr (A \rightarrow B) \geq Pr (B | A)} \) i jednakost vrijedi samo ako je \( {\small Pr (A) = 1 \text{ ili } Pr (A\overline{B}) = 0} \) tj. \( {\small Pr (A \rightarrow B) = 1} \).

Teorem o Pr (A→B) i Pr (B|A)

„Vjerojatnost od, B ako A“, tj. Pr (A→B), i „vjerojatnost od B, ako A“, tj. Pr (B|A), jednake su samo ako je Pr (A→B) = Pr (A) = 1, a inače je Pr (A→B) > Pr (B|A).

Probabilističku implikaciju među uvjetnim vjerojatnostima definiramo na isti način kao i među bezuvjetnim.

Opća definicija probabilističke implikacije

Pr (A₁|B₁) ∈ α₁, … , Pr (A_m|B_m) ∈ α_m ⊨  Pr (A|B) ∈ β    akko

(∀Pr) ( (∀i)Pr (A_i|B_i) ∈ α_i ⇒  Pr (A|B) ∈ β),

gdje su α_i,β neprazni intervali ⊆ [0,1].

Ova je definicija poopćenje prethodne definicije probabilističke implikacije, jer svaku bezuvjetnu vjerojatnost Pr (A) možemo shvatiti kao uvjetnu vjerojatnost Pr (A|U) u kojoj je U bilo koja tautologija.

Može se relativno lako dokazati da za probabilističku kontrapoziciju vrijedi sljedeći teorem.

Teorem o probabilističkoj kontrapoziciji

\( {\small Pr (A | B) = 1 \models Pr (\overline{B} | \overline{A}) = 1} \),

\( {\small Pr (A | B) = p \models Pr (\overline{B} | \overline{A}) \in [0,1]} \).

Interval [0,1] je optimalan, tj. ne može se suziti.

Dakle, ako znamo da je \( {\small Pr (A | B) = p} \)  onda o \( {\small Pr (\overline{B} | \overline{A})} \) ne znamo ništa. Na sličan način možemo dokazati da tada ni o \( {\small Pr (B | A)} \) ne znamo ništa, što je možda intuitivnije. Ranije smo vidjeli da vrijedi \( {\small Pr (A \rightarrow B) = p \models Pr (B \rightarrow A) \in [1 – p, 1]} \). No, \( {\small Pr (A \rightarrow B)} \) nije isto što i \( {\small Pr (B | A)} \), što smo već dokazali.

Zanimljiva su probabilističke varijante nekih standardnih načina dokazivanja, koje se također relativno lako dokazuju.

Teorem o probabilističkom dokazivanju po slučajevima

\( {\small Pr (B | A) = p, Pr (B | \overline{A}) = q \models Pr (B) \in [p, q]} \)

\( {\small Pr (B | A_{1}) = 1 – p, Pr (B | A_{2}) = 1 – p \models Pr (B | A_{1} \vee A_{2}) \in \left[1 – \frac{2p}{1 – p} , 1 – \frac{p}{2 – p}\right]} \)

Intervali u konkluzijama su optimalni, tj. ne mogu se suziti.

Teorem o probabilističkom modus ponensu

\( Pr (B | A) = p, Pr (A) = q \models Pr (B) \in [pq, 1 – pq] \\ ­ \\  Pr (B | A) \in [1 – p, 1], Pr (A) \in [1 – p, 1] \models Pr (B) \in [(1 – p)^2, 1] \)

Intervali u konkluzijama su optimalni, tj. ne mogu se suziti.

Drugu implikaciju još jednostavnije možemo izraziti preko rizika: Ako su rizici od A, i od B pod uvjetom A, oba manji od p onda je rizik od B manji od p².

Teorem o „pojačanoj“ probabilističkoj implikaciji

\( {\small Pr (B | A_{1}) = p, Pr (B | A_{2}) = q \models Pr (B | A_{1}A_{2}) \in [0, 1]} \)

Interval [0,1] je optimalan, tj. ne može se suziti.

Dakle, ako imamo A₁ kao svjedočanstvo za B (s vjerojatnošću p) i  A₂ kao svjedočanstvo za B (s vjerojatnošću q), ta dva svjedočanstva uzeta zajedno (bez dodatnih uvida) nisu nikakvo svjedočanstvo za B. Intuicija mnogih je da bi ta dva svjedočanstva uzeta zajedno trebala biti čak i jače svjedočanstvo od svakog pojedinog. Teorem tvrdi da to nije tako, a možemo ga uvjerljivije ilustrirati primjerom.

Policija zna da su zločin počinila dva muškarca, jedan u crvenoj jakni i drugi u crnom kaputu. Policija ima jednog osumnjičenog i dva svjedoka. Pitanje B jest je li osumnjičeni kriv. Prvi svjedok je osumnjičenog prepoznao kao muškarca u crvenoj jakni (to je A₁), a drugi kao muškarca u crnom kaputu (to je A₂). Očito je da svako pojedino svjedočanstvo ima neku vrijednost, dok oba zajedno nemaju nikakvu vrijednost.

Prvo izdanje knjige An Investigation of the Laws of Thought Georgea Boolea. (Manhattan Rare Books)

Ukoliko znamo Pr (A₁) i Pr (A₂) tada ipak nešto možemo zaključiti. To je dokazao Boole u svojoj knjizi An Investigation of the Laws of Thought iz 1851. Ta knjiga većim dijelom sadržava logiku vjerojatnosti, a tek manjim dijelom propozicijsku logiku, iako se to uglavnom zaboravilo. I za kraj evo teorema o probabilističkoj ne tranzitivnosti implikacije:

Teorem o ne tranzitivnosti probabilističke implikacije

\( {\small Pr (A_{3} | A_{2}) = p, Pr (A_{2} | A_{1}) = q \models Pr (A_{3} | A_{1}) \in [0, 1]} \)

Interval [0,1] je optimalan, tj. ne može se suziti.

Drugim riječima probabilistička implikacija nije tranzitivna čak ni u aproksimativnom smislu.

Time završavamo prikaz vjerojatnosti kao proširene logike, u ovom slučaju propozicijske logike. Proširenje na logiku 1. reda (kvantifikacijsku logiku) također je moguće, ali je bitno složenije. To proširenje na prirodan način smješta zakone velikih brojeva u prebrojivu vjerojatnost. To je posebno zanimljivo jer su ti zakoni u klasičnom pristupu Kolmogorova razumljivi samo u neprebrojivom kontekstu. Za one koji su spremni na nešto više matematike, na kraju ukratko i o tome.

• Vjerojatnost u prebrojivom kontekstu

Logika vjerojatnosti kvantifikacijskih formula dosta je složena i rekli smo da se njom nećemo baviti. Obradit ćemo nešto skromniju generalizaciju propozicijskih formula. Onu koja dopušta prebrojive  konjunkcije i alternacije.

S L_∞ označimo skup formula izgrađenih nad atomima uz pomoć veznika ∨, ∧  i –, uz mogućnost beskonačnih konjunkcija  \( {\small \bigwedge_{1}^{\infty} A_i } \) i beskonačnih alternacija  \( {\small \bigvee_{1}^{\infty} A_i } \) . Definicija funkcije istinitosti u biti je jednaka onoj s početka članka.

Definicija istinitosti na L_∞

Funkcija istinitosti V je svaka funkcija sa skupa L_∞ u skup {0, 1}, koja zadovoljava sljedeća pravila:

\( \text{(V1)} \quad V (A) + V (-A) = 1 \\ ­ \\ \text{(V2)} \quad V \left(\bigwedge_i A_i \right) = \max {V (A_i)} \\ ­ \\ \text{(V3)} \quad V \left(\bigvee_i A_i \right) = \min {V (A_i)} \\ \)

Za i ∈ {1, 2} to su obična propozicijska pravila. Za i ∈ N imamo željeno poopćenje.

Funkciju vjerojatnosti poopćujemo na sljedeći način.

Definicija vjerojatnosti na L_∞

Funkcija vjerojatnosti Pr je svaka funkcija sa skupa L_∞ u interval [0,1], koja zadovoljava sljedeća pravila:

\( \text{(P1)} \quad A \text{ je logički valjana} \Rightarrow Pr (A) = 1 \\ ­\\ \text{(P2$\vee$)} \quad A \text{ i } B \text{ se isključuju} \Rightarrow Pr (A \vee B) = Pr (A) + Pr (B) \\ ­ \\ \text{(P$\infty \vee$)} \quad Pr\left(\bigvee_{i=1}^{\infty} A_i \right) = \lim_{{n \to \infty}} Pr\left(\bigvee_{i=1}^{n} A_i \right) \\ \)

Pravilo (P_∞∨) ekvivalentno je pravilu \( {\small Pr\left(\bigwedge_{i=1}^{\infty} A_i \right) = \lim_{{n \to \infty}} Pr\left(\bigwedge_{i=1}^{n} A_i \right)} \), što je lako dokazati.

\( \large Pr\left(\bigwedge_{i=1}^{\infty} A_i \right) = Pr\left(\neg\neg \bigwedge_{i=1}^{\infty} A_i \right) = Pr\left(\neg\bigvee_{i=1}^{\infty} \neg A_i \right) = 1 – Pr\left(\bigvee_{i=1}^{\infty} \neg A_i \right)  \\ ­ \\  \large 1 – \lim_{{n \to \infty}} Pr\left(\bigvee_{i=1}^{n} \neg A_i \right) = 1 – \lim_{{n \to \infty}} Pr\left(\neg\neg\bigvee_{i=1}^{n} \neg A_i \right) = 1 – \lim_{{n \to \infty}} Pr\left(\neg\bigwedge_{i=1}^{n} A_i \right) \\ ­ \\ \large  1 – \left(1 – \lim_{{n \to \infty}} Pr\left(\bigwedge_{i=1}^{n} A_i \right)\right) = \lim_{{n \to \infty}} Pr\left(\bigwedge_{i=1}^{n} A_i \right) \)

Teorem o aditivnosti i  σ-aditivnosti

Ako se svi A_i međusobno isključuju onda vrijedi aditivnost:

\( {\small Pr \left(A_1 \vee A_2 \vee A_3 \vee \ldots \right) = Pr \left(A_1\right) + Pr \left(A_2\right) + Pr \left(A_3\right) + \ldots } \)

Bez uvjeta isključivanja vrijedi subaditivnost:

\( {\small Pr \left(A_1 \vee A_2 \vee A_3 \vee \ldots \right) \leq Pr \left(A_1\right) + Pr \left(A_2\right) + Pr \left(A_3\right) + \ldots } \)

Dokaz σ-aditivnosti:

\( {\small Pr\left(\bigvee_{i=1}^{\infty} A_i\right) = \lim_{{n \to \infty}} Pr\left(\bigvee_{i=1}^{n} A_i\right) = \lim_{{n \to \infty}} \sum_{i=1}^{n} Pr\left(A_i\right) = \sum_{i=1}^{\infty} Pr\left(A_i\right) } \)

Za dokaz σ-subaditivnosti umjesto drugog = treba staviti ≤.

Ako jezik L_∞ ima samo konačno mnogo atoma a₁, a₂, … , a_m onda ima 2^m konstituentata nad tim atomima i \( {\small 2^{2^m} } \) međusobno neekvivalentnih formula. U tom su slučaju beskonačne konjunkcije i alternacije ekvivalentne konačnima. Dakle, jezik koji izražava beskonačno mnogo međusobno ne ekvivalentnih tvrdnji nužno ima beskonačno mnogo atoma a₁, a₂, a₃, … . Definicija P-modela tada je nešto složenija od one s početka članka.

Definicija P-modela za beskonačno mnogo atomarnih formula

P-model za jezik  L_∞ izgrađen nad atomima a₁, a₂, a_3, … jest funkcija Pr iz skupa njihovih konstituenata {C₁, C₀, C₁₁, C₁₀, C₀₁, C₀₀, C₁₁₁, C₁₁₀, … } u interval [0,1], za koju, uz p_t = Pr (C_t), vrijedi

p₁ + p₀ = 1           p_t1 + p_t0 = p_t

Radi se o nizu konačnih P-modela za konačne skupove konstituenata {C₁, C₀}, {C₁₁, C₁₀, C₀₁, C₀₀}, …  koji odgovaraju konačnim skupovima atoma {a₁}, {a₁, a₂}, … .

Grafički prikaz jednog takvog  niza konstituenata i pridruženog niza modela je:

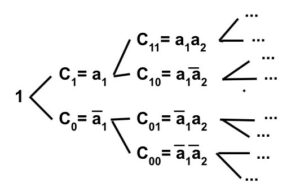
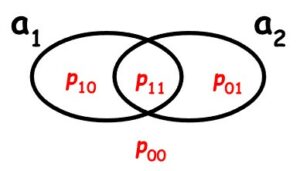
Konstituente C_t (gdje je svaki t slog 0-a i 1-a) možemo predstaviti i intervalima J_t ⊆ [0,1] za koje je

J₁ + J₀ = 1    J_t1 + Jt0 = Jt,

tako da njima pridružene vjerojatnosti p_t predstavljamo duljinama tih intervala |Jt|:

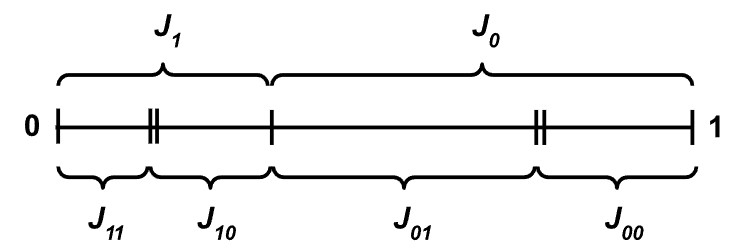
Vjerojatnosti u P-modelu definiramo kao i na početku ovoga članka.

Definicija vjerojatnosti formule iz L_∞ u P-modelu

Formula A jezika  L_∞ izgrađena nad atomima a₁ , a₂, a₂, … u modelu zadanom funkcijom Pr ima vjerojatnost

\( \text{Pr} (A) = \sum_A \text{Pr}(C_i ) = \sum_A p_i  \) ,

gdje se sumira po svim konstituentima C_i od kojih je izgrađena formula A.

Da se svaka formula A iz L_∞ može prikazati u obliku na koji se poziva gornja definicija ovdje nećemo dokazivati, kao ni to da se tom definicijom vjerojatnosti zadane modelom jednoznačno proširuju na sve forme iz  L_∞.

Definicija probabilističke implikacije ista je kao i prije. Njome se također nećemo baviti.

Émile Borel i Francesco Paolo Cantelli formulirali su slavni teorem o nizovima događaja u prvim desetljećima 20. stoljeća. (Creative Commons)

Kao primjer primjene prethodno definiranih pojmova dokazat ćemo slavnu Borel-Cantellijevu lemu koja rješava sljedeći Borelov problem iz 1909. Zamislite niz pokusa koji mogu rezultirati s uspjehom a₁ ili neuspjehom -a₁, uspjehom a₂ ili neuspjehom -a₂, uspjehom a₃ ili neuspjehom -a₃, itd. Ako znamo vjerojatnost uspjeha Pr (a_i) u svakom pojedinom pokusu, Borelov je problem odrediti vjerojatnost da beskonačni niz pokusa rezultira s beskonačno mnogo uspjeha, Pr (B). Rješava ga sljedeća lema.

Borel-Cantellijeva lema

Za tvrdnje Ai kažemo da su nizano nezavisne ako je svaka nezavisna od njoj prethodnih, tj. Pr (a₁ … a_n-1a_n) = Pr (a₁ … a_n-1) Pr (a_n) = … = Pr (a₁) … Pr (a_n-1) Pr (a_n).

\(  \text{Ako je } \sum_{i=1}^{\infty} \text{Pr}(a_i) < \infty \text{ onda je Pr}(B) = 0.  \\ ­ \\  \text{Ako je } \sum_{i=1}^{\infty} \text{Pr}(a_i) = \infty \text{ i ako su tvrdnje } A_i \text{ nizano nezavisne onda je Pr}(B) = 1.  \)

Evo dokaza. Vjerojatnosti Pr (a_i) kraće ćemo označiti s p_i. Tvrdnja B izraziva je u našem jeziku beskonačnih konjunkcija i alternacija na sljedeći način:

\( {\small B = \left( (a_1 \vee a_2 \vee a_3 \vee a_4 \vee \dots) \wedge (a_2 \vee a_3 \vee a_4 \vee \dots) \wedge (a_3 \vee a_4 \vee \dots) \wedge \dots \right) } \).

Dokaz prvog dijela leme je jednostavan. Za k →∞ imamo

\( B \models (a_k \vee a_{k+1} \vee a_{k+2} \vee \dots) \Rightarrow Pr (B) \leq Pr (a_k \vee a_{k+1} \vee a_{k+2} \vee \dots ) \leq p_k + p_{k+1} + p_{k+2} + \dots \rightarrow 0 \)

Zadnja nejednakost slijedi iz subaditivnosti, a limes je 0 jer repovi konvergentnog reda teže prema 0.

Dokaz drugog dijela leme malo je složeniji. Pretpostavimo da je \( \small{\sum_{i=1}^{\infty} p_i = \infty} \) i da su a_i nizano nezavisne tvrdnje. Nizovna nezavisnost od -a_i po dualnosti slijedi iz nizovne nezavisnosti od a_i pa vrijedi:

\( Pr(\bar{A_1} \bar{A_2} \bar{A_3} \ldots) = \lim_{{n \to \infty}} Pr(\bar{A_1} \ldots \bar{A_n}) = \lim_{{n \to \infty}} (1 – p_1) \ldots (1 – p_n) = \\ ­ \\ (1 – p_1)(1 – p_2)\ldots \leq e^{-p_1} e^{-p_2} \ldots = \exp(-(p_1 + p_2 + \ldots)) = e^{-\infty} = 0 \)

Dakle, vjerojatnost nijednog uspjeha u beskonačnom nizu jest 0. To znači da vjerojatnost  bar jednog uspjeha u beskonačnom nizu iznosi 1.

Sada niz (a_i) podijelimo na dva disjunktna podniza  (a‘_i) i (a”_i) za koje vrijedi  \( \small{\sum_{i=1}^{\infty} p’_i = \sum_{i=1}^{\infty} p”_i = \infty} \). Ponavljanjem prethodnog argumenta zaključimo da se u oba ta podniza, s vjerojatnošću 1, pojavljuje bar jedan uspjeh, tj. u početnom se nizu, s vjerojatnošću 1, pojavljuju bar 2 uspjeha. Analognim zaključivanjem nalazimo da se u početnom nizu, s vjerojatnošću 1, pojavljuje bar 4, 8, 16, 32, … uspjeha. Dakle, u nizu se, s vjerojatnošću 1, pojavljuje beskonačno mnogo uspjeha. Naime, ako s B_n označimo tvrdnju da se u početnom nizu pojavljuje bar 2ⁿ uspjeha onda je

\( \small{Pr (B) = Pr (B_1 B_2 B_3 \ldots) = \lim_{n \to \infty} Pr(B_1 \ldots B_n) = \lim_{n \to \infty} Pr(B_n) = \lim_{n \to \infty} 1 = 1} \).

• Vjerojatnost u neprebrojivom kontekstu

Nizova oblika ±a₁, ±a₂, ±a₃, … u kojima ±a_i može biti +a_i = a_i ili -a_i, ima neprebrojivo mnogo. Borel-Cantellijeva lema određuje kolika je vjerojatnost da takav niz sadrži beskonačno mnogo pozitivnih članova. Drugim riječima, lema određuje kolika je „gustoća“ nizova s beskonačno mnogo pozitivnih članova u neprebrojivom skupu svih nizova. Da bi odgovorila na tu vrstu pitanja standardna Kolmogorovljeva teorija vjerojatnosti konstruira prostor vjerojatnosti na tom neprebrojivom skupu.

Svaki niz možemo gledati kao niz 0-a i 1-a, tj. kao realan broj iz [0,1] u binarnom zapisu pa se problem svodi na definiranje vjerojatnosti na tom intervalu. Ako funkciju vjerojatnosti Pr definiramo kao b-a na svakom podintervalu [a,b] ⊆ [0,1] , pitanje je kako tu funkciju proširiti na složenije podskupove od [0,1]. Kolmogorov je 1933. dokazao da se skup svih podintervala može proširiti na σ-algebru (zatvorenu na komplemente te prebrojive presjeke i unije) tako da se polazna funkcija vjerojatnosti može jednoznačno proširiti na tu σ-algebru.

Ruski matematičar Andrej Nikolajević Kolmogorov postavio je svoje aksiome teorije vjerojatnosti 1933. godine. (Creative Commons)

Svaki konačni niz 0-a i 1-a predstavlja podinterval od [0,1]. To je podinterval svih onih beskonačnih nizova koji počinju tim konačnim nizom, npr. 01 predstavlja [1/4,1/2]. Zato vjerojatnosti zadane na konačnim nizovima 0-a i 1-a automatski zadaju vjerojatnosti na binarnim podintervalima intervala [0,1]. Da bismo dokazali Borel-Cantellijevu lemu moramo iz tih zadanih vjerojatnosti izračunati vjerojatnost skupa beskonačnih nizova s beskonačno mnogo 1-a. I za to nam treba Kolmogorovljeva teorija.

Ili nam ne treba? U prethodnom odjeljku smo prikazali dokaz Borel-Cantellijeve leme koji je neovisan o Kolmogorovljevoj teoriji. To je u biti Borelov dokaz iz 1909. zamišljen s eksplicitnom namjerom uvođenja „prebrojive vjerojatnosti“ smještene između „konačne vjerojatnosti“ i „neprebrojive vjerojatnosti“ koju je 1905. sam Borel uveo kao teoriju geometrijske vjerojatnosti.

Borel je inače smatrao da su „skupovi koji mogu biti definirani i suvislo razmatrani samo prebrojivi skupovi“ te da će neprebrojivi „kontinuum biti samo tranzicijski instrument, čija je današnja vrijednost nezanemariva, ali će u budućnosti biti smatran samo sredstvom za izučavanje prebrojivih skupova koji su nam jedini dostupni realitet“. Do danas mu se predviđanje nije ostvarilo. Danas većina matematičara ne vidi kako je uopće moguće tvrdnju o vjerojatnosti jednog neprebrojivog skupa dokazati u prebrojivom kontekstu. Zato ćemo to još jednom ilustrirati na primjeru zakona velikih brojeva.

Zamislimo niz nezavisnih identičnih pokusa koji mogu rezultirati uspjehom U s vjerojatnošću p, ili neuspjehom N s vjerojatnošću q = 1 – p. Možemo ga predstaviti sljedećim dijagramom.

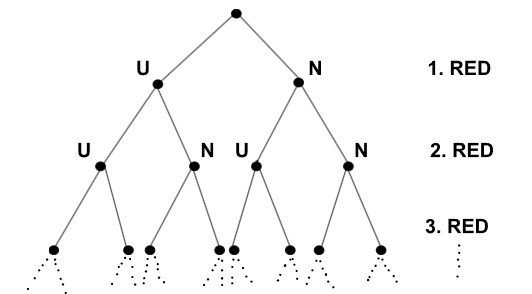
Mogući rezultati 1. pokusa prikazani su u 1. redu, 2. pokusa u 2. redu, 3. u 3. redu itd. Svaki čvor u n-tom redu određuje jednu moguću stazu koju čini n mogućih ishoda n ponovljenih pokusa. Ako u n-tom redu zaokružimo one čvorove na čijim se stazama frekvencija uspjeha f_n = U_n/n razlikuje od p za manje od ε, |f_n – p| ≤ ε, onda slabi zakon velikih brojeva tvrdi da gustoća zaokruženih čvorova u n-tom redu teži prema 1 kada n teži prema ∞. Drugim riječima, za svaki ε zastupljenost „ε-aproksimacija za p = f_n na razini n“ teži prema 1 kada n teži prema ∞.

To ne znači da frekvencija f_n teži prema p na svakoj beskonačnoj stazi. To je tema jakog zakona. On tvrdi da skoro sve beskonačne staze imaju skoro sve zaokružene čvorove, tj. da f_n teži prema p na skoro svim beskonačnim stazama. Naravno, „skoro svi“ ovdje ima značenja iz Borelove teorije mjere.

Dakle slabi zakon tvrdi:

\( (\forall \epsilon) \lim_{N \to \infty} Pr(|f_N – p| \leq \epsilon) = 1 \).

S druge strane, jaki zakon tvrdi:

\( Pr\left(\lim_{n \to \infty} f_n = p\right) = 1 \) tj.

\( Pr\left( \left( \forall \epsilon \right) \, \left( \exists N \right) \, \left( \forall n \geq N \right) |f_n – p| \leq \epsilon\right) = 1 \)

Dokazat ćemo da se kvantifikatori ∀ε i ∃N mogu izlučiti ispred Pr pa jaki zakon velikih brojeva možemo zapisati na sljedeći način:

\( \forall \epsilon \, \exists N : Pr\left(|f_N – p| \leq \epsilon \, \land \, |f_{N+1} – p| \leq \epsilon \, \land \, |f_{N+2} – p| \leq \epsilon \, \land \, \ldots\right) = 1 \)

Dakle, slabi i jaki zakon velikih brojeva možemo zapisati tako da su lako usporedivi:

\( \forall \epsilon : \lim_{{N \to \infty}} Pr\left(|f_N – p| \leq \epsilon\right) = 1 \\ ­ \\  \forall \epsilon : \lim_{{N \to \infty}} Pr\left(|f_N – p| \leq \epsilon \, \land \, |f_{N+1} – p| \leq \epsilon \, \land \, |f_{N+2} – p| \leq \epsilon \, \land \, \ldots\right) = 1 \)

Da je izlučivanje kvantifikatora ∀ε dopušteno dokazujemo na sljedeći način. Tvrdnja

\( Pr\left(\forall \epsilon \, \exists N \, \forall n \geq N : |f_n – p| \leq \epsilon\right) = 1 \)

ekvivalentna je s tvrdnjom

\( Pr\left(\forall \frac{1}{m} \, \exists N \, \forall n \geq N : |f_n – p| \leq \frac{1}{m}\right) = 1 \)

koja je ekvivalentna s tvrdnjom

\( Pr\left(\exists N_1 \, \forall n \geq N_1 : |f_n – p| \leq 1 \, \land \, \exists N_2 \, \forall n \geq N_2 : |f_n – p| \leq \frac{1}{2} \, \land \, … \right) = 1 \)

Zbog definicije „beskonačnih vjerojatnosti“ i činjenice da svaki konjunkt implicira sve prethodne slijedi da je

\( \small{\lim_{{m \to \infty}} Pr\left(\exists N \, \forall n \geq N : |f_n – p| \leq \frac{1}{m}\right) = 1} \)

No, to znači da je

\( \forall \frac{1}{m}, \, Pr\left(\exists N \, \forall n \geq N : |f_n – p| \leq \frac{1}{m}\right) = 1, \text{tj.} \, \\ ­ \\ \forall \epsilon, \, Pr\left(\exists N \, \forall n \geq N : |f_n – p| \leq \epsilon\right) = 1 \)

što smo i željeli dokazati.

Da je dopušteno izlučivanje kvantifikatora ∃N dokazujemo na sljedeći način. Tvrdnja

\( Pr\left(\exists N \, \forall n \geq N : |f_n – p| \leq \epsilon\right) = 1 \)

ekvivalentna je s tvrdnjom

\( Pr\left(\forall n \geq 1 : |f_n – p| \leq \epsilon \, \lor \, \forall n \geq 2 : |f_n – p| \leq \epsilon \, \lor \, \ldots\right) = 1 \).

Zbog definicije „beskonačnih vjerojatnosti“ i činjenice da svaka alternanta implicira sve sljedeće slijedi da je

\( \lim_{{K \to \infty}} Pr\left(\forall n \geq K : |f_n – p| \leq \epsilon\right) = 1 \)

Ako  (∀n ≥ K)|f_n – p| ≤ ε označimo s B_k, to znači da

\( (\forall \delta) (\exists N) (\forall K \geq N) \Pr(B_K) \geq 1-\delta \).

Zbog prethodnog limesa to je ekvivalentno s

\( (\forall \delta) (\exists N) \Pr(B_N) \geq 1-\delta, \text{ tj.} \).

\( (\forall \delta) (\exists N) \Pr \left( (\forall n \geq N) |f_n-p| \leq \epsilon \right) \geq 1-\delta \).

Što smo željeli dokazati.

Dokaz jakog zakona velikih brojeva sada slijedi iz \( \small{Pr\left(|f_n – p| \geq \varepsilon\right) \leq \frac{c}{{\varepsilon^4 n^2}}} \) , što slijedi, na primjer, iz Markovljeva teorema za slučajne varijable s konačnim 4. momentima (naravno, postoje i dokazi uz slabije uvjete). Naime,

\( \lim_{{N \to \infty}} \Pr\left(|f_N – p| > \varepsilon \vee |f_{N+1} – p| > \varepsilon \vee \ldots \right) \leq \\ ­ \\ \leq \lim_{{N \to \infty}} \left(\Pr\left(|f_N – p| > \varepsilon\right) \vee \Pr\left(|f_{N+1} – p| > \varepsilon\right) \vee \ldots \right) = \lim_{{N \to \infty}} \frac{c}{\varepsilon^4} \left(\frac{1}{N^2} + \frac{1}{{(N+1)^2}} + \ldots\right) = 0 \)

jer „rep“ konvergentne sume teži prema 0.

Kao dodatak za one koji znaju nešto teorije vjerojatnosti nudimo dokaz Markovljeva teorema i nejednakosti \(\small{ \Pr(|f_n – p| \geq \epsilon) \leq \frac{c}{{\epsilon^4 n^2}}} \) .

\( X \geq 0, a > 0 \Rightarrow X \geq X \cdot I(x \geq a) \geq a \cdot I(x \geq a) \)

gdje je I indikatorska funkcija koja je 1 ako je tvrdnja na koju se primjenjuje istinita, a 0 ako je neistinita. Slijedi da je očekivanje od X

\( E(X) \geq a(1 \cdot Pr(x \geq a) + 0 \cdot Pr(x < a)) \Rightarrow Pr(x \geq a) \leq \frac{E(X)}{a} \).

To je Markovljev teorem. Iz njega slijedi

\( Pr(X \geq a) = Pr(X^4 \geq a^4) \leq \frac{E(X^4)}{a^4} \) .

Primijenimo to na naš slučaj:

\( Pr\left(\frac{{U_n}}{n} \geq \varepsilon\right) = Pr\left(U_n \geq n\varepsilon\right) \leq \frac{{E(U_n^4)}}{{n^4\varepsilon^4}} \leq \frac{{Cn^2}}{{n^4\varepsilon^4}} = \frac{{C}}{{n^2\varepsilon^4}} \)

Posljednja nejednakost slijedi iz

\( E(U_n^4) = E (X_1 + \ldots + X_n)^4 = E\left(\sum_{1 \leq i,j,k,l \leq n} X_i X_j X_k X_l\right) = (i \neq j \neq k \neq l) = \\ ­ \\ m_1 E(X_i^3 X_j) + m_2 E(X_i^2 X_j X_l) + m_3 E(X_i X_j X_k X_l) + \left(\begin{array}{c} n \\ 1 \end{array}\right) E(X_i^4) + 6\left(\begin{array}{c} n \\ 2 \end{array}\right) E(X_i^2 X_j^2) = \\ ­ \\ nE(X^4) + 3n(n+1)E(X^2)^2 \leq cn^2 \)