Slobodna razmjena i pojava oligarhije. Siromaštvo je skupo, a početna prednost umnožava bogatstvo. Što ublažava neizbježni rast nejednakosti

Bruce M. Boghosian, matematičar sa Sveučilišta Tufts, objavio je potkraj prošle godine u časopisu Scientific American, simulaciju prema kojoj je nejednakost neizbježna posljedica tzv dvorišne razmjene pojedinaca koji u transakciju ulaze pretpostavljenom svojom voljom. Model prvo stvara oligarha, a kad se dodaju stvarni parametri, porezi, prednosti koje bogati imaju na tržištu te zaduživanje siromašnih, onda dobro opisuje današnju stvarnu rastuću nejednakost. Nudi i rješenje

• Članak preveo Pooka Zecov, poštar iz Dubrovnika

• Naslovna ilustracija: Youtube

• Original: Is Inequality Inevitable?

Nejednakost u bogatstvu ubrzava se alarmantnom brzinom ne samo unutar SAD-a već i u zemljama tako različitim kao što su Rusija, Indija i Brazil. Prema investicijskoj banci Credit Suisse, udio globalnog bogatstva kućanstava kojim raspolaže najbogatijih 1 posto svjetske populacije povećao se između financijske krize 2008. i 2018 godine s 42,5 posto na 47,2 posto. Drugačije rečeno, 2010. godine je 388 pojedinaca posjedovalo jednako bogatstvo kućanstva kao i kompletna donja polovica svjetske populacije – oko 3,5 milijarde ljudi, a danas Oxfam procjenjuje da je broj tih pojedinaca 26. Statistički podaci gotovo svih država koje mjere bogatstvo u istraživanjima svojih kućanstava pokazuju da to bogatstvo ubrzano postaje sve koncentriranije.

Iako se o razlozima nejednakosti žustro raspravlja, pristup koji su razvili fizičari i matematičari, uključujući moju grupu sa Sveučilišta Tufts, ukazuje na to da se oni već dugo skrivaju u na jednom očiglednom mjestu – u jednoj dobro poznatoj aritmetičkoj posebnosti. Ovaj pristup koristi modele raspodjele bogatstva zajednički poznate pod nazivom modeli utemeljeni na agentu (agent – based models) ili modeli izgrađeni na ponašanju sudionika u pojedinačnim transakcijama između dva ‘agenta’ ili sudionika, od kojih svaki pokušava optimizirati vlastiti financijski ishod. U modernom svijetu ništa ne može izgledati poštenije ili prirodnije od dvoje ljudi koji su odlučili razmijeniti robu, dogovorili se o cijeni i rukovali se. Doista, prividna stabilnost ekonomskog sustava koja proizlazi iz ove ravnoteže ponude i potražnje među pojedinačnim akterima smatra se vrhuncem prosvjetiteljskog razmišljanja do te mjere da su mnogi ljudi povezali slobodno tržište sa samim pojmom slobode. Naši na prvi pogled jednostavni matematički modeli, koji se temelje na dobrovoljnim transakcijama, ukazuju, međutim, na to da je došlo vrijeme za ozbiljno preispitivanje ove ideje.

‘Afini’ model bogatstva (koji se tako naziva zbog svojih matematičkih svojstava, objašnjen niže u članku, op.) može sa izvrsnom preciznošću opisati raspodjelu bogatstva među kućanstvima u zemljama na različitim stupnjevima razvoja, otkrivajući suptilnu asimetriju koja teži koncentriranju bogatstva. Vjerujemo da ovaj čisto analitički pristup, koji nalikuje rendgenskom snimanju jer se koristi ne toliko za predstavljanje kompleksne zbrkanosti u stvarnom svijetu, koliko za njeno uklanjanje i otkrivanje osnovnih struktura, pruža dubinski uvid u sile koje djeluju na povećanje siromaštva i nejednakosti danas.

• Oligarhija

Godine 1986. sociolog John Angle prvi put opisao kretanje i raspodjelu bogatstva koja proizlazi iz transakcija između dvoje agenata unutar skupine ‘ekonomskih agenata’, koji bi mogli biti pojedinci, kućanstva, tvrtke, fondovi ili drugi entiteti. Krajem stoljeća fizičari Slava Ispolatov, Pavel L. Krapivsky i Sidney Redner, koji su tada zajedno radili na Sveučilištu Boston, kao i Adrian Drgulescu, sada u Constellation Energy Group, i Victor Yakovenko sa Sveučilišta Maryland, pokazali su da bi se ovi modeli zasnovani na agentima mogli analizirati alatima statističke fizike, što dovodi do brzog napretka u našem razumijevanju njihovog ponašanja. Ispostavilo se da mnogi takvi modeli utvrđuju da se bogatstvo neumoljivo kreće jednosmjerno, od jednog agenta prema drugom – čak iako se temelje na poštenoj razmjeni između jednakih aktera. Anirban Chakraborti, tada na Saha Institutu za nuklearnu fiziku u Kolkati u Indiji, predstavio je 2002. godine ono što je poznato kao model dvorišne rasprodaje (yard sale model), nazvan tako jer ima određene značajke stvarnih ‘jedan na jedan’ ekonomskih transakcija. Također je koristio numeričke simulacije kako bi pokazao da one neumoljivo koncentriraju bogatstvo, što u konačnici rezultira oligarhijom.

Da biste razumjeli kako se to događa, pretpostavimo da ste u kockarnici i da ste pozvani da igrate jednu igru. Morate staviti malo pologa – recimo 100 USD – na stol nakon čega će novčić biti bačen. Ako novčić padne na glavu, kuća će vam platiti 20 posto onoga što imate na stolu, što rezultira 120 dolara na stolu. Ako novčić padne na pismo, kuća će uzeti 17 posto onoga što imate na stolu, što će rezultirati sa 83 dolara na stolu. Novac možete držati na stolu kroz koliko god želite bacanja novčića (a da ga nikad ne dodate ili oduzmete). Svaki put kad igrate, osvojit ćete 20 posto onoga što je na stolu ako novčić padne na glavu, a izgubit ćete 17 posto ako novčić padne na pismo. Bi li trebali pristati na ovu igru?

Mogli biste konstruirati dva argumenta, oba poprilično uvjerljiva, koji bi vam pomogli da odlučite što učiniti. Možda mislite: „Imam vjerojatnost ½ dobiti 20 dolara i vjerojatnost ½ gubitka 17 dolara. Stoga je moj očekivani dobitak:

½ x (20 USD) + ½ x (- 17 USD) = 1,50 USD

što je pozitivno. Drugim riječima, šanse za pobjedu i poraz su jednake, ali moj dobitak ako pobijedim bit će veći od gubitka ako izgubim.” Iz ove perspektive čini vam se korisnim igrati.

Ili biste poput šahista mogli razmišljati dalje u budućnost: „Što ako ostanem 10 bacanja novčića? Vjerojatan ishod je da će njih pet pasti glavom, a ostalih će pet pasti pismom. Svaki put kad padne glavom, moj polog se pomnoži s 1,2. Svaki put kad padne pismom, moj polog se pomnoži s 0,83. Nakon pet pobjeda i pet poraza bilo kojim redoslijedom, iznos novca koji ostaje na stolu bit će:

1,2 x 1,2 x 1,2 x 1,2 x 1,2 x 0,83 x 0,83 x 0,83 x 0,83 x 0,83 x 100 USD = 98,02 USD

pa ću izgubiti oko 2 dolara od svojih originalnih 100 dolara pologa.” Uz malo više kalkuliranja možete potvrditi da bi za nadoknađivanje 91 poraza bile potrebne oko 93 pobjede. Iz ove se perspektive čini ovu igru nepovoljnim igrati.

Proturječje između dva ovdje prikazana argumenta u početku se može činiti iznenađujućim, ali ono je dobro poznato u znanosti o vjerojatnosti i financijama. Njegova povezanost s nejednakošću bogatstva je, međutim, manje poznata. Da proširimo metaforu kockarnice na kretanje bogatstva u (izuzetno pojednostavljenoj) ekonomiji, zamislimo sustav od 1.000 pojedinaca koji se upuštaju u međusobne ‘jedan na jedan’ transakcije. Neka svaki započne s određenim početnim bogatstvom, koje bi bilo potpuno jednako. Nasumično odaberite dva agenta i pustite ih u transakciju, zatim učinite isto s još dva i tako dalje. Drugim riječima, ovaj model pretpostavlja sekvencijalne transakcije između slučajno odabranih parova agenata. Naš je plan provesti milijune ili milijarde takvih transakcija s našom populacijom od 1.000 i vidjeti kako se bogatstvo na kraju raspoređuje.

Kako bi trebala izgledati pojedinačna transakcija između jednog para agenata? Ljudi imaju prirodnu averziju prema potpunom gubitku, pa pretpostavljamo da je iznos koji je u pitanju, a koji nazivamo Δω (Δω izgovara se „delta w“), samo djelić bogatstva siromašnije osobe, Shaune. Na taj način, čak i ako Shauna izgubi u transakciji s Ericom, bogatijom osobom, iznos koji izgubi uvijek je manji od njezinog ukupnog bogatstva. To nije nerazumna pretpostavka i zapravo obuhvaća samonametnuto ograničenje koje većina ljudi instinktivno primjećuje i u svom ekonomskom ponašanju. Za početak – samo zato što su nam ovi brojevi poznati – pretpostavimo da je Δω 20 posto Shauninog bogatstva, ω, ako pobijedi i –17 posto ω ako izgubi. (Naš stvarni model pretpostavlja da su postoci pobjeda i poraza jednaki, ali općeniti ishod i dalje vrijedi. Štoviše, povećanje ili smanjenje Δω samo će produžiti vremensku ljestvicu tako da će biti potrebno više transakcija prije nego što uvidimo konačni rezultat, koji će ostati nepromijenjen.)

Ako je naš cilj modeliranje poštene i stabilne tržišne ekonomije, trebali bismo započeti pretpostavljajući da nitko nema bilo kakvu prednost pa ćemo bacanjem novčića odlučiti u kojem će se smjeru w pokrenuti. Ako novčić padne glavom, Shauna od Erica dobije još 20 posto svog bogatstva; ako novčić padne pismom, ona mora dati 17 posto svog bogatstva Ericu. Sada nasumce odaberite drugi par agenata od ukupno 1000 njih i ponovite to. Zapravo, samo naprijed i učinite to milijun puta ili milijardu puta. Što će se dogoditi?

Ako simulirate ovu ekonomiju, varijantu modela dvorišne rasprodaje (yard sale), dobit ćete izvanredan rezultat: nakon velikog broja transakcija jedan agent završit će kao ‘oligarh’ koji drži praktički sve bogatstvo gospodarstva, a drugih 999 završiti će s gotovo ničim. Nije važno s koliko su bogatstva ljudi započeli. Nije važno da su sva bacanja novčića bila apsolutno poštena. Nije važno što je očekivani ishod siromašnijeg agenta bio pozitivan u svakoj transakciji, dok je očekivani ishod bogatijeg agenta bio negativan. Bilo koji pojedinačni agent u ovoj ekonomiji mogao je postati oligarh – zapravo, svi su imali jednake šanse jer su započeli s jednakim bogatstvom. U tom je smislu postojala jednaka mogućnost. Ali samo je jedan od njih postao oligarh, a svi su ostali gledali kako im se prosječno bogatstvo smanjuje na nulu dok su izvršavali sve više transakcija. Da uvreda bude još veća, što je nečija razina bogatstva bila niža, to je pad bio brži.

Ovaj je ishod posebno iznenađujući jer vrijedi čak i ako su svi agenti započeli s jednakim bogatstvom i bili tretirani simetrično. Fizičari opisuju pojave ove vrste kao ‘kršenje simetrije’ [vidi Fiziku nejednakosti dolje]. Prvim okretanjem novčića novac se prebacuje od jednog agenta na drugog, što stvara neravnotežu između njih dvoje. A kad jednom imamo razliku u bogatstvu, koliko god minimalne one bile, buduće će transakcije sistematski premještati “kapljicu” (trickle) bogatstva prema gore, od siromašnijih prema bogatijima, pojačavajući nejednakost sve dok sustav ne postigne stanje oligarhije.

Ako je ekonomija u samom svom začetku nejednaka, bogatstvo najsiromašnijeg agenta vjerojatno će se najbrže smanjivati. Kamo ono ide? Bogatstvo najsiromašnijeg agenta mora ići bogatijim agentima jer od njega nema siromašnijih agenata. Stvari nisu puno bolje ni za drugoga najsiromašnijeg agenta. Dugoročno, svi sudionici ove ekonomije, osim onog najbogatijeg, gledat će kako njihovo bogatstvo eksponencijalno propada. U zasebnim radovima 2015. godine moji kolege i ja sa Sveučilišta Tufts i Christophe Chorro sa Sveučilišta Panthéon-Sorbonne prezentirali smo matematičke dokaze ishoda koji su Chakrabortijeve simulacije otkrile – da model dvorišne rasprodaje (yard sale) neumoljivo premješta bogatstvo s jedne strane na drugu.

Znači li to da siromašniji agenti nikad ne pobjeđuju ili da bogatiji agenti nikad ne gube? Sigurno ne. Još jednom, postavka nalikuje kockarnici – nekad dobijate, a nekad gubite, ali što duže ostanete u kockarnici, veća je vjerojatnost da ćete izgubiti. Slobodno tržište je u osnovi kockarnica iz kojeg nikada ne možete izaći. Kad se prethodno opisana ‘kapljica’ (trickle) bogatstva, koja se u svakoj transakciji prelijeva od siromašnog ka bogatom, pomnoži sa 7,7 milijardi ljudi na svijetu koji svake godine obavljaju nebrojene transakcije, ta kapljica postaje bujica. Nejednakost neizbježno postaje izraženija zbog kolektivnih učinaka ogromnog broja naizgled neutralnih, ali suptilno pristranih transakcija.

• Okrupnjavanje ili kondenzacija bogatstva

Mogli biste se, naravno, zapitati kakve veze ovaj model, čak i ako je matematički točan, ima sa stvarnošću. Uostalom, opisuje posve nestabilnu ekonomiju koja neminovno degenerira u potpunu oligarhiju, a na svijetu takve potpune oligarhije ne postoje. Istina je da sam po sebi model dvorišne rasprodaje (yard sale) nije u stanju objasniti empirijsku raspodjelu bogatstva. Kako bi riješila taj nedostatak i učinila ga realnijim, moja ga je grupa dopunila na tri načina.

Adrian Devitt-Lee, Merek Johnson, Jie Li, Jeremy Marcq, Hongyan Wang i ja, svi u Tuftsu, uključili smo 2017. godine u model i preraspodjelu bogatstva. U skladu s jednostavnošću poželjnom kod primijenjenih matematičkih modela, to smo postigli tako da smo napravili da se nakon svake transakcije svaki agent pomakne korak prema prosječnoj vrijednosti bogatstvu u društvu. Veličina koraka bila je neki dio χ (ili ‘chi’) udaljenosti agentovog bogatstva od vrijednosti prosječnog bogatstva. To je ekvivalent proporcionalnom porezu (flat tax) na bogatstvo za bogate (s poreznom stopom χ po jedinici vremena) i sukladnoj subvenciji za siromašne. Tom korekcijom u modelu se bogatstvo prenosi s onih agenata iznad prosjeka na one ispod prosjeka. Otkrili smo da je ova jednostavna modifikacija stabilizirala raspodjelu bogatstva tako da ona više nije nužno rezultirala oligarhijom. I, što je zapanjujuće, to je omogućilo našem modelu da replicira empirijske podatke o američkoj i europskoj raspodjeli bogatstva između 1989. i 2016. unutar greške manje od 2 posto. Pod ovim pojedinačnim parametrom χ pretpostavlja se mnoštvo stvarnih poreza i subvencija kojih bi bilo previše da se odvojeno uključe u jednostavan, strukturni model kao što je ovaj.

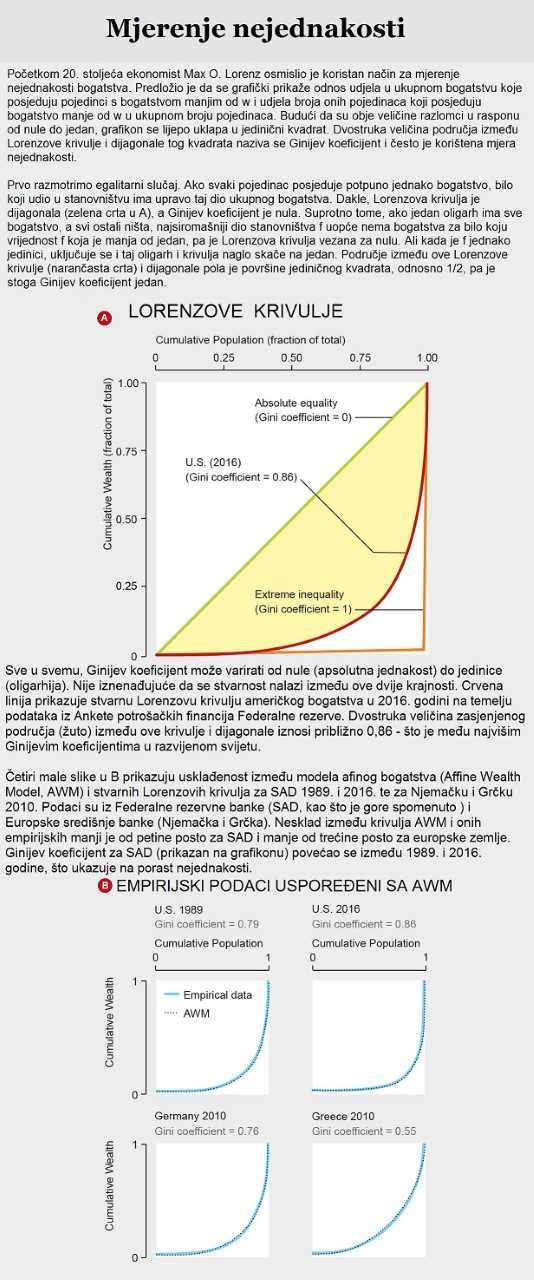
Uz to, empirijski je vrlo dobro dokumentirano da bogati uživaju sustavne ekonomske prednosti kao što su niže kamatne stope na zajmove i pristup boljim financijskim savjetima, dok siromašni trpe sustavne ekonomske nedostatke kao što je to izrazito nepovoljno kratkoročno zaduživanje i nedostatak vremena za kupovinu po najboljim cijenama. Kao što je James Baldwin jednom primijetio – “Svatko tko se ikad borio sa siromaštvom zna kako je izuzetno skupo biti siromašan.” U skladu s tim, u istom gore spomenutom radu uzeli smo u obzir ono što nazivamo prednošću stečenog bogatstva (wealth-attained advantage). Uveli smo pristranost kod bacanja novčića u korist bogatijeg pojedinca za iznos proporcionalan novom parametru, ζ (ili ‘zeta’), pomnoženom s razlikom bogatstva agenta podijeljenom sa srednjim bogatstvom. Ova poprilično jednostavna korekcija, koja služi kao zamjena za mnoštvo pristranosti koje favoriziraju bogate, poboljšala je usklađenost između našeg modela i gornjeg dijela (upper tail) stvarne raspodjele bogatstva.

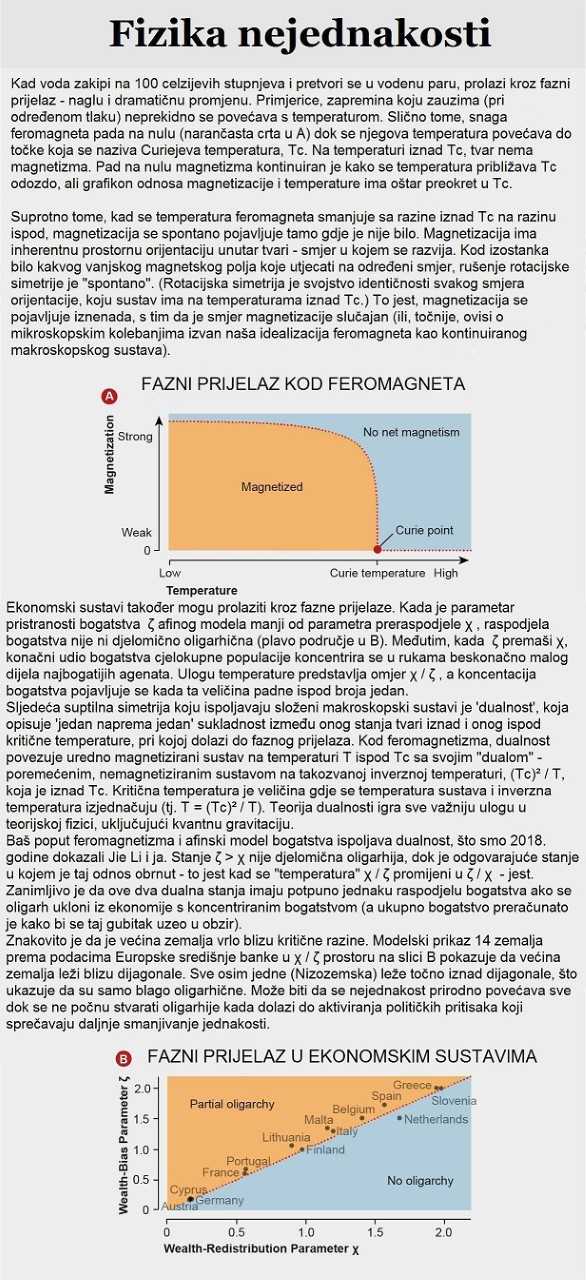
Uključivanje pristranosti vezane za bogatstvo također donosi – i daje preciznu matematičku definiciju – fenomenu djelomične oligarhije. Kad god prednost stečenog bogatstva premaši utjecaj preraspodjele (točnije, kad god ζ pređe χ), sve manji i manji broj agenata posjedovat će ograničenu veličinu, 1 – χ / ζ, konačnog dijela društvenog bogatstva. Početak djelomične oligarhije zapravo je fazna tranzicija prema drugom modelu ekonomskih transakcija, modelu koji su prvi put 2000. godine opisali fizičari Jean-Philippe Bouchaud, sada na École Polytechnique, i Marc Mézard iz École Normale Supérieure. U našem modelu, kada je ζ manje od χ, sustav ima samo jedno stabilno stanje bez oligarhije; kada ζ premaši χ, pojavljuje se novo, oligarhijsko stanje koje postaje stabilno (vidi sliku). Tako dobiveni model dvorišne rasprodaje (yard sale model) s dva parametra (χ i ζ) može se podudarati s empirijskim podacima o raspodjeli bogatstva iz SAD-a i Europe između 1989. i 2016. godine, unutar raspona od 1 do 2 posto.

Bouchaud i Mézard, čiji model koncentracije bogatstva možda može objasniti što se u Rusiji dogodilo nakon raspada Sovjetskog Saveza i nametanja šok-terapije

Takva fazna tranzicija možda je imala presudnu ulogu u koncentraciji bogatstva nakon raspada Sovjetskog Saveza 1991. godine. Nametanje onoga što se nazivalo ekonomijom šok-terapije bivšim državama SSSR-a rezultiralo je dramatičnim smanjenjem preraspodjele bogatstva (odnosno smanjenje χ) od strane njihovih vlada i popratni skok prednosti stečenog bogatstva (povećanje ζ) zbog kombiniranih učinaka nagle privatizacije i nagle deregulacije. Rezultirajući pad ‘temperature’ χ / ζ bacio je zemlje u stanje koncentracije bogatstva, tako da su bivše komunističke zemlje gotovo preko noći postale djelomične oligarhije. Do današnjeg dana se barem 10 od 15 bivših sovjetskih republika može točno opisati kao oligarhije.

U model su uključeni pristranost na strani bogatih, što odražava njihove šire tržišne mogućnosti, te  negativno bogatstvo – jedan od uznemirujućih aspekata modernih ekonomija. Primjerice, 2016. godine, približno 10,5 posto stanovništva SAD-a bilo je u neto dugu zbog hipoteka, studentskih zajmova i drugih čimbenika

Kao treće usavršavanje, 2019. godine u svoj smo model uključili negativno bogatstvo – jedan od uznemirujućih aspekata modernih ekonomija. Primjerice, 2016. godine, približno 10,5 posto stanovništva SAD-a bilo je u neto dugu zbog hipoteka, studentskih zajmova i drugih čimbenika. Stoga smo uveli treći parametar, κ (ili ‘kappa’), koji pomiče raspodjelu bogatstva prema dolje, uzimajući tako u obzir i negativno bogatstvo. Pretpostavili smo da je najmanje bogatstvo koje bi najsiromašniji agent mogao imati u bilo kojem trenutku –S, gdje je S jednako κ puta prosječno bogatstvo. Prije svake transakcije posudili smo bogatstvo S obojici agenata tako da je svaki imao pozitivno bogatstvo. Zatim su agenti izvršili transakcije prema ranije opisanom modelu dvorišne rasprodaje, nakon čega su oboje otplatili svoj dug S.

Tako dobiveni model s tri parametra (χ, ζ, κ), nazvan afinim modelom bogatstva, može se podudarati s empirijskim podacima o američkoj raspodjeli bogatstva s manje od šestine jednog postotka (0,17%) u rasponu od tri desetljeća. (U matematici riječ “afini” opisuje nešto što se multiplikativno skalira i dodatno translira. U ovom slučaju, neke značajke modela, poput vrijednosti Δω, multiplikativno se skaliraju sa bogatstvom agenta, dok druge značajke, kao što je npr. zbrajanje ili oduzimanje S, dodatne su translacije ili pomaci u ‘prostoru bogatstva’.) Podudaranje s europskim podacima o raspodjeli bogatstva za 2010. godinu obično je od trećine pa do pola postotka [vidi okvir dolje].

Da bismo dobili te usporedbe sa stvarnim podacima, morali smo riješiti ‘inverzni problem’. Odnosno, morali smo pronaći vrijednosti (χ, ζ, κ) prema kojima bi se rezultati našeg modela najbliže podudarali s podacima o empirijskoj raspodjeli bogatstva. Kao jedan od primjera, najbolje opisana raspodjela bogatstva kućanstava u SAD-u iz 2016. godine je ona sa vrijednostima modela: χ = 0,036, ζ = 0,050 i κ = 0,058. Afini model bogatstva primijenjen je na empirijske podatke iz mnogih zemalja i epoha i, koliko je nama poznato, opisuje podatke o raspodjeli bogatstva preciznije od bilo kojeg drugog postojećeg modela.

• Kapanje prema gore

Smatramo vrijednim pažnje da je dosad najprikladniji model za prikaz empirijske raspodjele bogatstva onaj koji bi bio potpuno nestabilan bez preraspodjele, a ne onaj zasnovan na navodnoj ravnoteži tržišnih sila. Zapravo, ovi matematički modeli pokazuju da je daleko od toga da se bogatstvo cijedi prema siromašnima (trickle down), prirodna sklonost bogatstva da teče prema gore, tako da je “prirodna” raspodjela bogatstva u ekonomiji slobodnog tržišta ona koja vodi u potpunu oligarhiju. Preraspodjela je jedina sila koja postavlja ograničenje nejednakosti.

Matematički modeli također skreću pozornost na veličinu razmjera utjecaja kršenja simetrije na raspodjelu bogatstva kroz slučajnosti i rane prednosti (na primjer, kroz nasljeđivanje). A prisutnost kršenja simetrije dovodi u pitanje i argumente o pravednost nejednakosti bogatstva koji pozivaju na ‘dobrovoljnost’ – na ideju da pojedinci snose svu odgovornost za svoje ekonomske ishode jednostavno zato što dobrovoljno ulaze u transakcije – ili na ideju da akumulacija bogatstva mora biti rezultat pametnosti i marljivosti. Istina je da položaj pojedinca u rasponu raspodjele bogatstva donekle korelira s takvim atributima, ali ukupni oblik tog raspona može se objasniti statističkim modelom preciznim do razine od 0,33 posto koji ih potpuno ignorira. Sreća igra mnogo važniju ulogu nego što joj se obično priznaje, tako da su vrlina koja se u modernom društvu obično pripisuje bogatstvu – i, slično tome, stigma koja se pripisuje siromaštvu – potpuno neopravdane.

Štoviše, samo pažljivo osmišljen mehanizam za preraspodjelu može nadoknaditi prirodnu tendenciju bogatstva u tržišnoj ekonomiji da se kreće od siromašnih prema bogatima. Preraspodjela se često miješa s porezima, ali ta dva pojma bi trebalo držati poprilično odvojenim. Porez teče od ljudi prema njihovim vladama kako bi se financirale aktivnosti tih vlada. Preraspodjelu, za razliku od toga, mogu provoditi vlade, ali najbolje se o njoj misli kao o protoku bogatstva od ljudi do ljudi kako bi se ispravila nepravednost inherentna tržišnoj ekonomiji. U proporcionalnoj (flat) shemi preraspodjele, svi koji imaju bogatstvo ispod prosjeka dobili bi neto sredstva, dok bi oni iznad prosjeka platili. I upravo zato što su trenutne razine nejednakosti tako ekstremne, puno bi više ljudi dobilo nego što bi platilo.

S obzirom na to koliko su stvarne ekonomije komplicirane, drago nam je što jednostavan analitički pristup koji su razvili fizičari i matematičari opisuje stvarnu raspodjelu bogatstva više nacija s preciznošću i točnošću bez presedana. Također je prilično zanimljivo da ove distribucije prikazuju suptilne, ali ključne značajke složenih fizičkih sustava. Najvažnije je, međutim, to što bi skica slobodnog tržišta tako jednostavna i moguća kao što je to afini model bogatstva, a koja nužno vodi u ekonomije koje su sve samo ne slobodne i poštene, trebala biti i uzrok za uzbunu i poziv na akciju.