Vjerojatnost kao frekvencija. Rasprava empirista i racionalista, britanskog i kontinentalnog pristupa. Žilavi argument

Na početku Zvonimir Šikić (ponovo) opisuje vjerojatnost kao frekvenciju u populaciji, što je zapravo klasični pojam vjerojatnosti iz prethodnog članka, te predstavlja stablo frekvencija kao lakši način razumijevanja onog što se izračunava Bayesovom formulom. Zatim objašnjava vjerojatnost kao frekvenciju u ponavljanom pokusu i probleme s kojima se taj koncept suočava (granična frekvencija, prebrojiva aditivnost). Napokon, distinkciju klasičnog i frekventističkog pojma vjerojatnosti diže na razinu rasprave empirista i racionalista. Završava Bernoullijevom pogreškom

• Naslovna ilustracija: Britanski filozof John Stuart Mill prvo je vjerojatnosti pristupio empiristički, britanski, no uskoro je promijenio mišljenje (Foto: Wikipedia)

• Prethodni članak: Klasična vjerojatnost i primjeri povijesnog razvoja

• Vjerojatnost kao frekvencija u populaciji

Vjerojatnost nekog obilježja u nekoj populaciji često se identificira s relativnom frekvencijom tog obilježja u toj populaciji. Na primjer, vjerojatnost bijele kugle u kutiji s 3 bijele i 22 crne kugle je 3/25 = 0.12 (tj. vjerojatnost da slučajno izvučemo bijelu kuglu iz te kutije je 0.12). Ili, vjerojatnost da prvo dijete koje će se roditi 2023. bude dječak je 0.51, jer je to relativna frekvencija muškaraca u populaciji ljudi. To je zapravo klasični pojam vjerojatnosti koji se temelji na jednakoj vjerojatnosti odabira svakog člana populacije, jer je tada (prema klasičnoj metodi povoljni/mogući) vjerojatnost nekog obilježja u toj populaciji upravo njegova relativna frekvencija.

Sve smo to već koristili u mnogim primjerima prethodnoga članka. Ovdje to još jednom naglašavamo samo iz psiholoških razloga, jer postoje jaki argumenti da ljudi mnogo lakše razumiju frekvencije nego (njima ekvivalentne) vjerojatnosti. To ćemo najbolje ilustrirati konkretnim primjerom koji smo već obradili u prethodnom članku.

1. Problem pozitivnog testa. Želite li utvrditi da li bolujete od neke bolesti, podvrći ćete se testu. Ako je test pozitivan onda ste bolesni, a ako je negativan onda ste zdravi (tako bar mislite vi i mnogi liječnici). No, nijedan test nije savršeno pouzdan, pa za stvarnu procjenu vašeg stanja valja znati kolika je pouzdanost testa. Pretpostavimo da je senzitivnost testa 90%, tj. vjerojatnost da bolesna osoba bude pozitivna je 90%. Pretpostavimo da je specifičnost toga testa, tj. vjerojatnost da zdrava osoba bude negativna, također je 90%. Dakle, Pr (+| B) = 0.9 i Pr (-| Z) = 0.9. Koliko vas mora zabrinuti pozitivni nalaz, te s kolikim olakšanjem možete prihvatiti negativni nalaz ako nemate drugih indikacija da ste bolesni, osim provedenoga testa?

Rješenje. Brzopleti odgovor: pouzdanost testa je 90% pa pozitivni test garantira bolest s vjerojatnošću 90%, a negativni test garantira zdravlje s vjerojatnošću 90%.

To je daleko od istine. Nacrtajmo, kako smo objasnili u prvom nastavku ove serije, odgovarajuće stablo frekvencija (dakle, s frekvencijama umjesto vjerojatnosti):

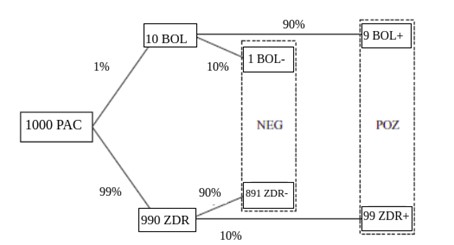
Zamislili smo 1000 testiranih ljudi. Ako je učestalost bolesti koju testirate 1% onda je samo 10 od tih 1000 ljudi uistinu bolesno a 990 je zdravo.

Od 990 zdravih, njih 891 je negativno (90% od 990), a njih 99 je pozitivno (10% od 990).

Od 10 bolesnih, njih 9 je pozitivno (90% od 10), a samo 1 je negativan (10%od 10).

Ukupno je 108 (tj. 99+9) pozitivnih od kojih je 9 bolesno. Dakle, vjerojatnost da ste bolesni ako ste pozitivni je 9/108 što je oko 8%:

Pr (B | +) = 8%.

To je daleko od 90% koji su vas toliko zabrinuli.

Kao i u prvom nastavku ove serije, negativni test garantira vam zdravlje s vjerojatnošću mnogo bližom pouzdanosti (senzitivnosti i specifičnosti testa). Naime, ukupno imamo 892 (tj. 891+1) negativnih od kojih je 891 zdravo, pa je vjerojatnost da ste zdravi ako ste negativni 891/892 što je 99,999%:

Pr (- | Z) = 99,999%.

Pogreška da se pozitivni nalaz smatra 90% garancijom bolesti još je jednom pogreška brkanja Pr (+| B) sa Pr (B | +); prva je vjerojatnost 90%, a druga tek 8%.

U prethodnom nastavku ove serije napomenuli smo da ljudi mnogo lakše rezoniraju sa stablima vjerojatnosti nego s Bayesovom formulom. Sada možemo dodati da još bolje rezoniraju sa stablima frekvencija. Iako su sve te metode logički ekvivalentne, psihološki se bitno razlikuju. Zato nije nebitno koju ćemo, kada i kome predstaviti kao metodu rješavanja probabilističkih problema. Samo manji broj eksperata uspješno se koristi Bayesovom formulom, više ljudi svlada tehniku stabala vjerojatnosti, a još više uspješno se koristi stablima frekvencija. Naravno, daleko najviše ih ne razumije nijednu od tih metoda, niti se njima koristi. Budući da su problemi koje rješavaju te (međusobno ekvivalentne) metode važni i toj velikoj većini, poželjno je formulirati neka jednostavna pravila kojima se i ta većina može koristiti.

Dva takva veoma jednostavna pravila za bolju procjenu pozitivnog i negativnog testa objavio sam 2021. u Journal of Evaluation in Clinical Practice. Prije nego ih formuliram, ponovit ću neke standardne pojmove. Senzitivnost testa je vjerojatnost da će testirana osoba biti pozitivna pod uvjetom da je bolesna, Pr (+ | B). Specifičnost testa je vjerojatnost da će testirana osoba biti negativna pod uvjetom da je zdrava, Pr (- | Z). Zajedničkim ih imenom zovemo pouzdanostima testa. Manju od tih vjerojatnosti zvati ćemo minimalnom, a veću maksimalnom pouzdanošću testa.

No, liječnike i pacijente ne zanimaju te vjerojatnosti. Njih zanimaju vjerojatnosti da je testirana osoba bolesna ako je pozitivna, Pr (B | +) i da je zdrava ako je negativna, Pr (Z | -). Te vjerojatnosti zovu se pozitivna i negativna prediktivna vrijednost. Senzitivnost i specifičnost testa ne ovise o učestalosti bolesti. Prediktivne vrijednosti, a one nas zanimaju, izrazito ovise o učestalosti bolesti i to još nije dovoljno shvaćeno.

Sljedeća tablica prikazuje odnos između učestalosti bolesti i prediktivnih vrijednosti u testu koji je  95% pouzdan, tj. i senzitivnost i specifičnost su mu 95%.

Učestalost bolesti u populaciji	Pozitivna prediktivna vrijednost (bolesni ako su pozitivni)	Negativna prediktivna vrijednost (zdravi ako su negativni)
0.1%	2%	99.99%
1%	16%	99.9%
5%	50%	99%
10%	67%	99%
30%	89%	97%
50%	95%	95%
70%	98%	89%
90%	99%	67%
95%	99%	50%

Dakle, ako je učestalost bolesti vrlo niska i vi ste pozitivni, vjerojatnost da ste bolesni ipak je vrlo niska. Uz malu učestalost bolesti, pozitivan ne znači bolestan.

Vidjeli smo kako se prediktivne vrijednosti mogu računati pomoću Bayesove formule ili pomoću stabla vjerojatnosti i upozorili da liječnici i pacijenti često imaju problema s razumijevanjem tih metoda. Upoznali smo se i sa stablom frekvencija koje je Gigerenzer predložio kao prihvatljiviju metodu za ispravno provođenje bejesovskih zaključaka. Zahvaljujući njegovim naporima, posljednjih desetak godina medicinske škole širom svijeta počele su podučavati tu metodu kako bi mladim liječnicima pomogli razumjeti rezultate testiranja. No, kako rekosmo, mnogi liječnici i dalje nisu u stanju procijeniti prediktivne vrijednosti iz relevantnih zdravstvenih statistika pa još uvijek brkaju pouzdanosti testa s njegovim prediktivnim vrijednostima.

To nije samo netočno, već je i opasno. Mjesecima nakon primanja lažno pozitivnog mamograma, žene osjećaju anksioznost koja pogubno utječe na njihov život i svakodnevno raspoloženje. Osobe s lažno pozitivnim testom na HIV upuštaju se u seks bez zaštite s drugim HIV-pozitivnim osobama, vjerujući da to više nije važno.  Mnogi počine i samoubojstvo. Sve je to u literaturi bogato dokumentirano.

Dakle, pravilo pozitivan = bolestan & negativan = zdrav pogrešno je i opasno. No, ono je mnogo jednostavnije od Bayesove formule i njenog stabla vjerojatnosti pa i od  Gingerenzerovog stabla frekvencija. Nažalost, ljudi se često drže jednostavnih pravila, bila ona ispravna ili ne pa je veoma korisno imati jednostavna pravila koja su ispravna. Takva su moja dva pravila.

POZITIVNO PRAVILO
Ako je zbroj maksimalne pouzdanosti i učestalosti manji od 100% i vi ste pozitivni,
onda je vjerojatnost da ste bolesni manja od 50%.

Na primjer, ako je učestalost bolesti 4%, specifičnost testa je 85%, senzitivnost testa 95% i vi ste pozitivni, šansa da ste bolesni manja je od 50%, jer je 95% + 4% < 100%.

Važno je primijetiti da pozitivno pravilo jasno upozorava da je testiranje promašeno ako je učestalost bolesti mala. Ono ima smisla samo ako se ograničimo na testiranje uže populacije u kojoj je učestalost bolesti veća (a to je populacija s relevantnim simptomima i drugim kliničkim indikatorima).

NEGATIVNO PRAVILO
Ako je učestalost bolesti manja od 50% i vi ste negativni, onda je vjerojatnost da niste bolesni veća od minimalne pouzdanosti.

Na primjer, ako je učestalost bolesti manja od 50%, specifičnost testa je 90%, osjetljivost testa je 95% i vi ste negativni, vaša je šansa da ste zdravi veća od 90%.

Vjerujem da bi ova pravila mogla biti od velike pomoći i liječnicima i pacijentima.

(Prethodno opisana psihološka problematika nije samo pedagoško pitanje nego je jedan od važnih razloga razmimoilaženja između Kahnemana, Tverskog i drugih zastupnika tzv. naivnih heuristika s Gigerenzerom i drugim evolucijskim psiholozima, oko razumijevanja ljudske racionalnosti. O tome vidi: Gigerenzer vs. Kahneman. Kako ljudi stvarno razmišljaju. Koliko procjena točnosti jednog dijagnostičkog testa ima veze s vjerojatnošću?

• Vjerojatnost kao frekvencija u ponavljanom pokusu

Upravo obrađena „vjerojatnost kao relativna frekvencija u populaciji“ zapravo je klasični pojam vjerojatnosti baziran na jednako vjerojatnim elementarnim događajima, koja je dodatno zanimljiva samo psihološki. No, kada nije moguće naći jednako vjerojatne elementarne događaje na koje bismo sveli traženu vjerojatnost relativna frekvencija postaje naša jedina vodilja. Na primjer, bacimo li čavlić on može pasti tako da mu vrh gleda gore ili dolje (v. sliku). Ta dva ishoda nisu simetrična, pa ne možemo zaključiti da su jednako vjerojatni. Da bismo otkrili kolika je vjerojatnost ishoda G (vrh gleda gore) i D (vrh gleda dolje), moramo čavliće bacati više puta i iskustveno ustanoviti kolika je relativna frekvencija ishoda G, a kolika ishoda D.

Pr (G) ≈ relativna frekvencija događaja   Pr (D) ≈ relativna frekvencija događaja D

U skladu s tim, mnogi vjerojatnost (bar približno) definiraju kao relativnu frekvenciju.

Vjerojatnost događaja A približno je jednaka relativnoj frekvenciji pojavljivanja toga događaja pri ponavljanju slučajnoga pokusa velik broj puta:

Pr (A) = n(A)/n.

U formuli je n ukupni broj pokusa, a n (A) je broj onih pokusa u kojima se desio A.

Dakle, vjerojatnost događaja jest relativna frekvencija njegovog pojavljivanja u dugom nizu ponovljenih slučajnih pokusa. Ili kraće, vjerojatnost je „dugotrajna relativna frekvencija“. (Nadalje ćemo relativnu frekvenciju jednostavnije zvati frekvencijom.)

• Empirijska ‘dedukcija’ aksioma vjerojatnosti

Ova definicija dokaze glavnih svojstava vjerojatnosti, tj. aksioma vjerojatnosti, čini vrlo jednostavnima, kao i u slučaju klasične vjerojatnosti iz prethodnog nastavka ove serije. Zato ih je i Kolmogorov koristio kao motivaciju svoje aksiomatske teorije vjerojatnosti iz 1933. (pod primjerenim naslovom “Empirijska dedukcija aksioma”).

Naime, ako je n (A) broj događaja A koji su se dogodili u n ponovljenih slučajnih pokusa, ako je f_n (A) = n (A) /n odgovarajuća frekvencija i ako je f_n (B|A) frekvencija događaja B u slučajevima u kojima se  dogodio A, onda očito vrijedi:

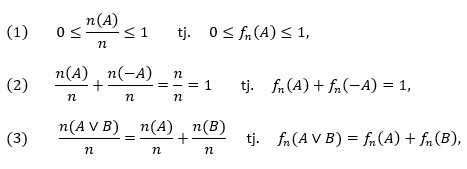
ako se A i B isključuju

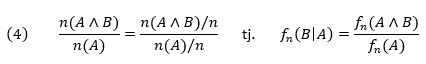
Naravno, ako je f_n = Pr onda su (1) – (4) aksiomi vjerojatnosti:

(1) 0 ≤ Pr (A) ≤ 1,

(2) Pr (A) + Pr (–A) = 1,

(3)  Pr (A ∨ B) = Pr (A) + Pr (B),

ako se A i B isključuju

(4)  Pr (A ∧ B) = Pr (A) Pr (B|A), gdje je Pr (B|A) vjerojatnost od B ako se zbio A.

• Problemi s graničnom frekvencijom

Ali, ovdje postoji jedan veliki problem. Za koji n je f_n vjerojatnost? Je li vjerojatnost glave određena frekvencijom glave u 100 bacanja kovanice tj. sa f₁₀₀, je li određena sa 1000 bacanja, tj. sa f₁₀₀₀ ili s nekom drugom frekvencijom? Koliko duga treba biti „dugotrajna relativna frekvencija“?

Problem bi mogla zaobići „najduža od svih dugotrajnih relativnih frekvencija““, tj. ona koja je beskonačno duga. Stoga bismo mogli definirati:

No, ovo rješenje problema stvara nove probleme. Za razliku od konačnih frekvencija, ovako definirane granične frekvencije neopažljive su. Granična frekvencija nema empirijski sadržaj. Uostalom, dva beskonačna niza, koji se ne razlikuju na početku, koliko god dug on bio, mogu imati različite granične frekvencije. Dakle, ne postoji veza između graničnih frekvencija i konačnih opažljivih frekvencija. Naravno, ako nas zanima matematički temelj vjerojatnosti, a ne nužno i njene primjene, mogli bismo se pozabaviti matematičkom teorijom graničnih frekvencija.

Dakle, istražimo matematiku vjerojatnosti Pr, koja je definirana kao . Sigurno je povoljno da ovako definirana vjerojatnost zadovoljava aksiome vjerojatnosti (jer ih zadovoljavaju sve frekvencije f_n). Ali to je tako samo ako postoji , a lako je konstruirati primjere beskonačnih nizova s nepostojećim graničnim frekvencijama.

Evo jednog takvog primjera u kojem ne postoje granične frekvencije glava i pisama:

GP GP GGPP GGGGPPPP GGGGGGGGPPPPPPPP …

Niz počinje s GP GP, a nakon toga, za svaki n > 0, imamo blokove s 2ⁿ G-ova i 2ⁿ P-ova. Ako se zaustavimo nakon n-tog bloka, frekvencija glava će biti ½, jer svaki blok ima isti broj glava i pisama. Ako se zaustavimo u sredini n-tog bloka, frekvencija glava će biti:

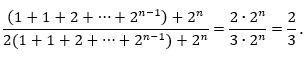
Dakle, frekvencija pojavljivanja glava u ovom nizu oscilira između 1/2 i 2/3, tj. granična frekvencija pojavljivanja glava u ovom nizu ne postoji.

Nadalje, čak i ako beskonačan niz glava i pisama ima graničnu frekvenciju, postoji beskonačno mnogo podnizova toga niza s kojom god graničnom frekvencijom želite (pored beskonačno mnogo njih bez granične frekvencije). Dakle, ako na odgovarajući način zanemarite neka bacanja, možete dobiti što god želite.

Pretpostavimo, nadalje, da su rezultati ponovljenih eksperimenata “glava-pismo” raspoređeni u prostoru i vremenu na sljedeći način:

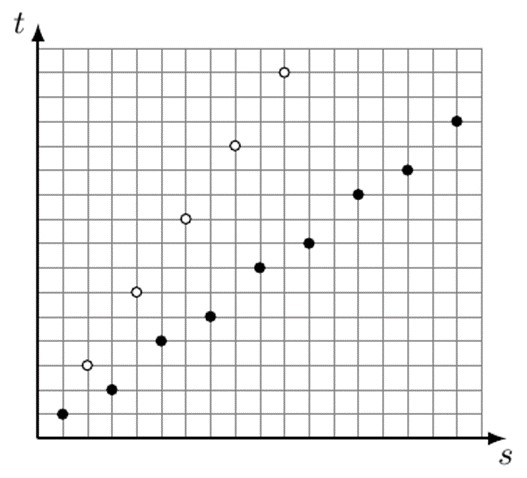
Glave su predstavljene bijelim točkama. Njihove koordinate su parcijalne sume niza:

(2,3) + (2,3) + (2,3) + (2,3) + (2,3) + …

Pisma su predstavljena crnim točkama. Njihove koordinate su parcijalne sume niza:

(1,1) + (2,1) + (2,2) + (2,1) + (2,2) + (2,1) + (2,2) + …

Ako ste vi bacali kovanicu, vaš vremenski niz glava i pisama je:

PPG PPG PPG …

Granična frekvencija glava u vašem vremenskom nizu je 1/3 i to je vaša procjena vjerojatnosti glave.

Ako ja na tlu pregledavam kovanice koje ste vi bacili pomičući se u smjeru osi s, moj prostorni niz glava i pisama izgleda ovako:

GP GP GP GP GP …

Granična frekvencija glava u mojem prostornom nizu je ½ i to je moja procjena vjerojatnosti glave.

Treba li jedan odgovor biti točan, a drugi pogrešan?

• Misesovi kolektivi

Kao rješenje ovih problema Richard von Mises je 1936. predložio isključivanje prethodno opisanih problematičnih nizova. Dakle, nizovi eksperimentalnih rezultata

(1) trebaju imati granične frekvencije i

(2) te granične frekvencije trebaju biti iste u svakom beskonačnom, ali izračunljivom, podnizu zadanog niza.

Samo su takvi nizovi „slučajni“ i stoga podobni za definiranje vjerojatnosti kao granične frekvencije. Mises ih je zvao „kolektivima“. Pojašnjenje da podniz mora biti efektivno izračunljiv uveo je Church 1940.

Prethodno opisani “niz glava i pisama bez granične frekvencija” isključen je zahtjevom (1). Podnizovi “s kojom god graničnom frekvencijom želite” isključeni su zahtjevom (2). Ipak, ranije opisana osjetljivost na „prostor i vrijeme“ nije isključena. Pretpostavljam da taj primjer, koji je danas donekle poznat, u Misesovo vrijeme nije bio. Da jest, Mises bi gotovo sigurno takve anomalije isključio zahtjevom:

(3) granične frekvencije trebaju ostati iste u svakom izračunljivom preuređenju zadanog niza.

Ali Mises nije uspio objasniti zašto bi beskonačan niz slučajnih pokusa bio „kolektiv“, tj. zašto bi beskonačan niz glava i pisama generiranih beskonačnim nizom slučajnih pokusa trebao zadovoljavati (1) – (3). O tome više u jednom od sljedećih nastavaka.

• Prebrojiva aditivnost

Daljnji problem za frekventiste je prebrojiva aditivnost kojom se tvrdi da aditivnost vjerojatnosti vrijedi i za beskonačno mnogo događaja D_i koji se međusobno isključuju:

Pr (D₁ ∨ D₂ ∨ D₃ ∨ D₄ ∨ …) = Pr (D₁) + Pr (D₂) + Pr (D₃) + Pr (D₄) + …

Kolmogorov u Foundations of the Theory of Probability iz 1933. (kojom je utemeljio matematičku teoriju vjerojatnosti) naprosto postulira prebrojivu aditivnost, jer će tom dodatnom idealizacijom „pojednostaviti svoju matematiku“, iako je “gotovo nemoguće razjasniti njeno empirijsko značenje, kao što je to učinjeno za [druge] aksiome”.

Od onda se uvriježilo mišljenje da za tu dodatnu idealizaciju niti ima niti može biti frekvencijske motivacije. Standardni protuprimjer koji navodno dokazuje točnost tog uvriježenog mišljenja sljedeća je lutrija s beskonačno mnogo žetona 1, 2, 3,4, … . Ako je Dj propozicija “izvučen je žeton j” i ako pretpostavimo da u beskonačnom nizu izvlačenja (sa zamjenama) niti jedan od žetona nije izvučen beskonačno mnogo puta onda je Pr (D_j) = (D_j) = 0, za svaki j pa iz toga slijedi da je

Pr (D₁) + Pr (D₂) + Pr (D₃) + Pr (D₄) + … = 0.

S druge strane Pr (D₁ ∨ D₂ ∨ D₃ ∨ D₄ ∨ …) = 1, jer je  D₁ ∨ D₂ ∨ D₃ ∨ D₄ ∨ … nužni događaj. Dakle

Pr (D₁ ∨ D₂ ∨ D₃ ∨ D₄ ∨ …) = 1 ≠ 0 = Pr (D₁) + Pr (D₂) + Pr (D₃) + Pr (D₄) + …

To naizgled pobija prebrojivu aditivnost. Ali zašto bi Pr (D₁) + Pr (D₂) + Pr (D₃) + Pr (D₄) + … trebalo biti 0? To je neodređeni oblik ∞·0 koji može biti bilo što, ako se još sjećate svog prvog kolegija infinitezimalnog računa. Zapravo, u ovom konkretnom slučaju lako je dokazati da taj zbroj jest 1, kao što i treba biti prema prebrojivoj aditivnosti.

Pretpostavimo, na primjer, da beskonačan slijed izvlačenja počinje ovako:

D₄, D₁, D₁, D₂, D₄, D₁, D₇, D₂ …

Tada su odgovarajuće vjerojatnosti:

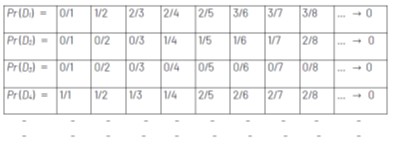
Ako zbrojimo sve stupce dobivamo:

Pr (D₁) + Pr (D₂) + Pr (D₃) + Pr (D₄) + … =

lim ( 1/1, 1/2 + 1/2, 2/3 + 1/3, 2/4 + 1/4 + 1/4, …) = lim ( 1, 1, 1, 1, …)  = 1

Izračun je isti za svaki niz izvlačenja. Naime, ako je F_j broj izvučenih j-žetona u prvih n izvlačenja onda je zbroj vrijednosti u n-tom stupcu , gdje je ukupni broj svih žetona izvučenih u prvih n izvlačenja, koji je očito n pa je = 1. Dakle, granične frekvencije zadovoljavaju prebrojivu aditivnost u ovom konkretnom primjeru. (Uočite da u dokazu nismo koristili granične vrijednosti iz zadnjeg stupca.)

No, istim argumentom lako dokazujemo prebrojivu aditivnost sasvim općenito. Neka se D₁, D₂, D₃ … međusobno isključuju. Definirajmo D kao D₁ ∨ D₂ ∨ D₃ ∨ … . Tada se -D, D₁, D₂, D₃ … također međusobno isključuju i prethodnim argumentom “zbrajanja po stupcima” (usp. napomenu o ne korištenju graničnih vrijednosti iz zadnjeg stupca) nalazimo da je

Pr (-D) + Pr (D₁) + Pr (D₂) + Pr (D₃) + … = lim (1, 1, 1, 1 …) = 1

Iz toga slijedi da je

Pr (-D ∨ D) = Pr (-D) + Pr (D) = 1 = Pr (-D) + Pr (D₁) + Pr (D₂) + Pr (D₃) + … tj.

Pr (D) = Pr (D₁) + Pr (D₂) + Pr (D₃) + … .

Dakle, granične relativne frekvencije zadovoljavaju aksiome vjerojatnosti (1) – (4) (što je dobro poznato), a zadovoljavaju i prebrojivu aditivnost (što sam upravo dokazao, a 2013. i objavio). Stoga granične relativne frekvencije nemaju problema s aksiomima vjerojatnosti. Njihov problem je što možda ne postoje, tj. beskonačan niz slučajnih pokusa  možda nema graničnu frekvenciju. Tom ćemo se pitanju vratiti u jednom od sljedećih nastavaka ovog serijala.

U aksiomatizaciji vjerojatnosti Kolmogorov prebrojivu aditivnost naprosto postulira. (Wikipedia)

• Empiristi i racionalisti

Klasični pojam vjerojatnosti iz prvog nastavka ovog serijala primjenljiv je u situaciji u kojoj možemo osmisliti slučajni pokus koji opisuje tu situaciju i koji je dovoljno simetričan da mu elementarni događaji budu jednako vjerojatni. Takve su simetrije najčešće prisutne u igrama na sreću i sličnim artificijelnim situacijama, ali npr. ne i u gore opisanom primjeru bacanja čavlića. U takvim nesimetričnim situacijama frekventisti vjerojatnost identificiraju s „dugotrajnom relativnom frekvencijom“. Mi smo ta dva pristupa prikazali komplementarnima, ali frekventisti često inzistiraju da je jedino njihova definicija valjana (bez obzira na sve probleme na koje smo ukazali), jer je „klasična definicija neprimjenljiva, budući da je empirijska provjera potrebnih simetrija u krajnjoj liniji opet frekventistička“. Taj sukob frekventista i klasičara, na čijoj strani su i bejesovci, (usp. daljnje nastavke ovog serijala) star je više stoljeća, a počeo kao jedan je od aspekta sukoba britanskih empirista i kontinentalnih racionalista.

Na primjer, britanski empirist John Stuart Mill matematiku i logiku (bila ona induktivna ili deduktivna) opravdava iskustveno pa mu je bliži frekvencijski pogled na vjerojatnost. U prvom izdanju svoje knjige System of Logic iz 1843. on ismijava Laplaceov klasični pojam vjerojatnosti – koji Laplace izvodi iz bejesovskog shvaćanja vjerojatnosti propozicije kao stupnja njene plauzibilnosti. Ali tri godine kasnije, u drugom izdanju, Mill mijenja stav i postaje laplasovac. Naime, astronom John Herschel objasnio mu je da nije razumio Laplacea. Osim toga upozorio ga je na mnoge nekonzistentnosti frekventizma. Slično, John Venn koji je pokušao sistematski izložiti  frekvencijski pogled, napada Laplaceove vjerojatnosti i njihovog britanskog proponenta Augustusa De Morgana, ali suočen s problemima identificiranja vjerojatnosti s frekvencijama ne uspijeva naći konzistentni temelj za svoj frekvencijski stav.

S druge strane, kontinentalni racionalisti Gottfried Wilhelm Leibniz, Jacob Bernoulli, Laplace i drugi ne identificiraju vjerojatnosti s frekvencijama. Za njih je vjerojatnost racionalni stupanj uvjerenja. No ipak ih zanima koja je formalna veza između frekvencija i tako shvaćenih vjerojatnosti. Bernoulli je uspio odgovoriti na dio tog pitanja, sa svojim zakonom velikih brojeva koji je 1713. objavio u knjizi „Ars Conjectandi“:

Uz odabir dovoljno dugog niza pokusa, relativna frekvencija ishoda aproksimira vjerojatnost tog ishoda s kojom god želite preciznošću.

Dakle, „britanske“ relativne frekvencije uspješno aproksimiraju „kontinentalne“ vjerojatnosti. To je Bernoulli zvao svojim zlatnim teoremom. Na primjer, ako je vjerojatnost ishoda 0.6, i ako je željeni interval aproksimacije (0.58, 0.62), a željena vjerojatnost da frekvencija padne u taj interval je 0.999, onda iz zlatnog teorema slijedi da se to postiže ako je broj pokušaja veći od 25 550.

Zlatnim teoremom Bernoulli je pokušao ali nije uspio iz dovoljno dugog niza pokusa odrediti vjerojatnost uspjeha u pojedinom pokusu. (Wikipedia)

• Bernoullijeva greška

Motivacija za zlatni teorem bila je Bernoullijeva želja da iz empirijskih podataka određuje vjerojatnosti, jer je respektirao upozorenje frekventista da u mnogim područjima nije moguće odrediti vjerojatnosti na klasičan način, prebrajanjem jednako vjerojatnih slučajeva. Želio je iz dovoljno dugog niza pokusa i frekvencija uspjeha u tim pokusima, odrediti kolika je vjerojatnost uspjeha u pojedinom pokusu. Evidentno je da Bernoulli nije riješio taj problem. Riješio je smjer od vjerojatnosti k frekvencijama, ali ne i smjer od frekvencija k vjerojatnostima. Ipak, Bernoulli je vjerovao da je riješio problem prijelaza od frekvencija na vjerojatnosti pozivajući se na sljedeći (pogrešni) argument. Ako je uz dovoljno veliki broj pokusa relativna frekvencija približno jednaka vjerojatnosti, onda je uz taj broj pokusa i vjerojatnost približno jednaka relativnoj frekvenciji pa je problem zaključivanja od frekvencija k vjerojatnosti riješen.

Taj argument zvuči uvjerljivo: ako je onda je . No, pokušate li ga precizirati argument se raspada. Naime, aproksimacija  ima po volji veliku vjerojatnost za dovoljno velike n, pod uvjetom da je p vjerojatnost uspjeha u svakom pojedinom pokusu (to je zlatni teorem). To ne znači da aproksimacija ima po volji veliku vjerojatnost za dovoljno velike n, pod uvjetom da je f_n relativna frekvencija uspjeha u n ponovljenih pokusa. Iako su  i ekvivalentne tvrdnje, uvjeti pod kojima procjenjujemo njihove vjerojatnosti su različiti pa su to i njihove vjerojatnosti. Na primjer, kada bi druga tvrdnja bila točna onda bi frekvencije f_n nužno konvergirale prema graničnoj vrijednosti p, za što nisu dani nikakvi argumenti.

„Argument“ da zakon velikih brojeva omogućava prijelaz od relativnih frekvencija na vjerojatnost nevjerojatno je žilav. Preživio je do danas u formi Fisherovog p-testa, o čemu će još biti riječi. Sam zaključak tog argumenta (bez ozbiljnije rasprave o samom argumentu) ponavljali su vrlo ugledni teoretičari vjerojatnosti 20. stoljeća, uključujući Émilea Borela, Paula Lévyja, Andreja Markova i Andreja Kolmogorova. Kako je to moguće? Diaconis, jedan od velikana teorije vjerojatnosti koji upozorava na taj problem, misli da je to bila strategija ignoriranja problema vezanih uz interpretaciju pojma vjerojatnosti, kojom se zapravo izbjegavao ozbiljan pokušaj suočavanja s tim problemima.

Primijetimo još da cijela ova rasprava (i sam zakon velikih brojeva) ima smisla tek za one koji pretpostavljaju da postoji vjerojatnost uspjeha u jednom pokusu, klasičare i bejesovce. Samo se oni mogu pitati je li tu vjerojatnost moguće aproksimirati relativnim frekvencijama ponavljanih pokusa. Ako ste frekventist za kojeg vjerojatnost jest granična frekvencija onda je izlišno pitati se je li graničnu frekvenciju moguće aproksimirati frekvencijama (to je tautologija, ako ta granica postoji, a baš je to postojanje problem).