Jednostavnost je prednost rimskih brojeva. Egipatsko množenje i intuitivno zbrajanje

Rimski brojevi bili su jednostavniji i intuitivniji za opću populaciju, koja je stoljećima bila slabo obrazovana u Europi, piše Aleksandar Hatzivelkos u svojem doprinosu raspravi zašto je tranzicija s rimskih na arapske brojeve trajala gotovo pet stotina godina. Osnovne matematičke operacije s rimskim brojevima - zbrajanje, oduzimanje i množenje - zahtijevale su korištenje znatno manje informacija i znatno nižu razinu apstrakcije od arapskih brojeva.

• Naslovna fotografija: Datum posvećenja župne crkve u Loferu. (Wolfgang Sauber / CC BY-SA 3.0)

• Autor je matematičar i profesor stručnog studija na Veleučilištu Velika Gorica. Politički je aktivan u sklopu stranke Možemo od 2019. godine.

Posljednjih par mjeseci na portalu Ideje.hr otvorila se rasprava o upotrebi rimskih, odnosno indo-arapskih brojevnih sustava u Europi, te neobično dugom periodu potrebnom da se s jednog brojevnog sustava (rimskog) prijeđe na drugi (indo-arapski). Vjerujem da s tekstovima Željka Ivankovića i Zvonimira Šikića tema nije iscrpljena te se može sadržajno dopuniti, upravo u traženju odgovora na osnovno pitanje – zašto je toj tranziciji trebalo gotovo pet stotina godina?

Temu je otvorio Željko Ivanković prenoseći ideje i stavove lingvističkog antropologa Stephena Chrisomalisa, koji u svojoj knjizi propituje veću efikasnost indo-arapskog pozicijskog brojevnog sustava u usporedbi s rimskim ne-pozicijskim brojevnim sustavom. Tako Chrisomalis kao osnovnu tezu navodi da „notacija brojeva dakle ne služi prvenstveno računanju nego bilježenju veličina (rezultata)“, te kao argument navodi da se za provođenje računskih operacija u to doba pretežno koristio abakus, baš kao što se i danas za provođenje računa oslanjamo na računala.

Uslijedila je reakcija Zvonimira Šikića koji svojim tekstom ukazuje na temeljni problem rimskih brojeva – izostanak sustavnog prikaza i računa s razlomcima, što se pokazalo i ključnim nedostatkom u daljnjem razvoju matematike, prvenstveno logaritama.

Oba teksta, više ili manje eksplicitno, podrazumijevaju veću efikasnost indo-arapskog brojevnog sustava u provođenju osnovnih aritmetičkih operacija, poput zbrajanja i oduzimanja, a posebno množenja. Štoviše, taj je sentiment naglašen citatom iz Chrisomalisove knjige: „Jeste li ikad pokušali tim (rimskim) brojevima množiti?“, pri čemu je autor (kako to Ivanković prenosi) izlaz potražio u tada korištenim efikasnim tehnikama računanja, poput abakusa.

Rimski brojevi uistinu jesu, ograničavajući faktor za razvoj matematike, no opća populacija nije koristila logaritme, kao ni precizne astronomske izračune

Teza koju bih ovim tekstom želio izložiti čitateljima jest: u oba slučaja se s argumentacijom o (ne)efikasnosti rimskog brojevnog sustava ide predaleko. Time hoću reći da se u analizi razloga za (ne)prihvaćanje indo-arapskih brojeva ide u smjerovima koji nisu doticali opću populaciju tog doba. Rimski brojevi uistinu jesu, kako navodi Šikić, ograničavajući faktor za razvoj matematike. No opća populacija nije koristila logaritme, kao ni precizne astronomske izračune. S druge strane, abakus jest iznimno efikasan način računanja, u pojedinim primjenama i značajno efikasniji od algoritama koje koristimo u indo-arapskom brojevnom sustavu. No dug proces prelaska s jednog brojevnog sustava na drugi nije (isključiva) zasluga efikasnosti abakusa. Jer ni abakus nije sredstvo koje se široko koristilo u općoj populaciji.

Opća populacija tog vremena je uglavnom bila neobrazovana ili slabo obrazovana. No i tada su svim ljudima bile potrebne efikasne metode za jednostavno provođenje osnovnih aritmetičkih operacija. Doslovno svatko se u nekom trenutku našao u poziciji da je morao zbrojiti, oduzeti, pomnožiti ili podijeliti dva broja.

Teza koju iznosim glasi da je rimski brojevni sustav (usprkos ograničenjima koje je nametao razvoju matematike kao znanosti) po jednostavnosti i efikasnosti provođenja računa bio superioran indo-arapskom brojevnom sustavu u općoj populaciji tog vremena. Štoviše mislim da se to može dobro demonstrirati upravo odgovarajući na pitanje – „Jeste li ikad pokušali tim (rimskim) brojevima množiti?“

­­

Rimsko zapisivanje brojeva zahtijeva manje učenja i apstraktnog razmišljanja. (Frank Griesshammer/CC BY-SA-NC 2.0)

Svi smo u dobroj mjeri upoznati s načinom zapisivanja rimskih brojeva: on koristi oznake I (za jedan), V (za pet), X (za deset), L (za pedeset), C (za sto), D (za pet stotina) i M (za tisuću). Istaknimo da se u prvom periodu za pisanje brojeva koristila samo inačica u kojoj se vrijednost broja dobiva isključivo zbrajanjem vrijednosti tih simbola, pa se recimo broj četiri pisao IIII, a ne IV, gdje se vrijednost (manjeg) lijevog simbola (jedan) oduzima od vrijednosti (većeg) desnog simbola (pet). Štoviše, upravo se ta aditivna varijanta (IIII) koristila u samom procesu računanja i kasnije kada je uvedena „pokrata“ zapisa (IV). Stoga ćemo se nje držati i u ovom tekstu. Pri tome postoje pravila zapisa, svojevrsna sintaksa: simboli I, X i C mogu se ponavljati najviše četiri puta, a simboli V, L i D se ne smiju ponavljati, odnosno piše ih se samo jednom.

Prva teza

Takav način zapisivanja brojeva je značajno jednostavniji od indo-arapskog, tj. zahtijeva daleko manje učenja i apstraktnog razmišljanja.

Simbol X uvijek predstavlja vrijednost deset, za razliku od znamenke (simbola) 1, koja može značiti jedan, deset, sto, tisuću, i tako dalje, ovisno o poziciji na kojoj se nalazi. Očigledno je da drugi zapis zahtijeva višu razinu apstrakcije. Što je važan faktor kad je većina korisnika slabo ili nikako obrazovana.

Druga teza

Zbrajanje je značajno jednostavnije kod rimskih brojeva.

Zbrajanje se kod rimskih brojeva provodi konkatenacijom, odnosno lijepljenjem. Na primjer ako želimo zbrojiti brojeve XVI (16) i XXVIII (28), brojeve jednostavno:

(a) zapišemo zajedno  (XVIXXVIII);

(b) znamenke poredamo od najveće prema najmanjoj (XXXVVIIII);

(c) provedemo jednostavno zbrajanje osnovnih znamenki (VV je jednako X, pa je rješenje broj XXXXIIII).[1]

Iako se zbrajanje provodi kroz konkatenaciju, očigledno je potrebno poznavati dodatna pravila za interakciju između znamenki. No tih je pravila malo, samo šest (IIIII=V, VV=X, XXXXX=L, LL=C, CCCCC=D i DD=M).

S druge strane, kod zbrajanja u indo-arapskom brojevnom sustavu, koristimo se višom razinom apstrakcije (značenje pozicije na kojoj se nalazi znamenka, te prenošenje vrijednosti s jedne pozicije na drugu) i moramo pamtiti značajno veći broj interakcija znamenki, točnije, njih \(\small \left( \begin{array}{c} 10 \\ 2 \end{array} \right) = 45\).

Treća teza

Oduzimanje je jednostavnije kod rimskih brojeva.

Kod rimskih se brojeva oduzima poništavanjem istih znamenki u umanjeniku i umanjitelju. Primjerice, ako oduzimamo brojeve XXII (22) i VIII (8) postupak provodimo tako da:

(a) uklonimo iste znamenke (XXII-VIII = XX-VI);

(b) znamenku umanjenika napišemo pomoću manjih znamenki, npr. X kao VIIIII (XX-VI = XVIIIII-VI), te se vratimo na korak(a). Postupak ponavljamo dok ne uklonimo sve znamenke umanjitelja. Dakle:

XXII-VIII = XX-VI = XVIIIII-VI =XIIII.

Vidimo da se postupak oduzimanja svodi na poznavanje osnovnih šest odnosa između znamenki, te na vizualno poništavanje istih dijelova brojeva koje oduzimamo.

S druge strane, pri oduzimanju brojeva u indo-arapskom zapisu, kao i kod zbrajanja, moramo koristiti veći broj informacija (odnosi između znamenki koje se oduzimaju) i višu razinu apstrakcije (prenošenje vrijednosti na novu poziciju).

Četvrta teza

Množenje je jednostavnije kod rimskih brojeva.

Upravo je množenje ključna točka ovog priloga raspravi. Množenje rimskih brojeva nije široko poznat proces. Algoritam koji se koristio zapravo nije vezan isključivo uz brojeve u rimskom zapisu, već ga je moguće provesti u bilo kojem brojevnom sustavu u kojemu znamo (po mogućnosti jednostavno):

• Prepoznati parni od neparnog broja
• Pomnožiti broj s dva
• Cjelobrojno podijeliti broj s dva

Sama tehnika koja se koristila u rimskom brojevnom sustavu zapravo potječe iz starog Egipta, odnosno, radi se o blago modificiranom algoritmu koji se danas još naziva i seljačko množenje (eng. peasant multiplication).

Prije samog algoritma prokomentirajmo tri navedene pretpostavke.

Što se neparnih brojeva tiče, jedine neparne znamenke u rimskim brojevima su znamenke I i V. Stoga se neparan rimski broj prepoznavao po (ukupnom) neparnom broju tih znamenki. Tako je broj XVII neparan jer ima neparan broj (tri) znamenki V i I, dok je broj XVIII paran jer ima paran broj (četiri) znamenki V i I.

Rimske brojeve iznimno jednostavno množimo s dva: broj se dva puta zapiše, pa se provede korekcija poretka i pojednostavljivanje zapisa kao kod zbrajanja. Tako na primjer broj XVII (17) pomnožen s dva iznosi: XVIIXVII = XXVVIIII = XXXIIII, dakle 34.

Kada govorimo o cjelobrojnom dijeljenju, govorimo o funkciji koju u modernoj matematici zapisujemo pomoću oznaka  (koje pak čitamo „najveće cijelo“), a radi se o rezultatu dijeljenja kod kojeg odbacujemo/zanemarujemo ostatak. Tako bi cjelobrojno dijeljenje prirodnog broja n s dva u modernoj matematici zapisali kao \(\left\lfloor \frac{n}{2} \right\rfloor\), pri čemu vrijedi \(\left\lfloor \frac{8}{2} \right\rfloor\) = 4, ali i \(\left\lfloor \frac{9}{2} \right\rfloor\) = 4. U oba slučaja rezultat dijeljenja je četiri, pri čemu u prvom slučaju nema ostatka, a u drugom slučaju je ostatak jednak jedan. Kako cjelobrojno dijeljenje zanemaruje ostatak, rezultat dijeljenja brojeva 8 i 9 s 2 je isti i iznosi 4.

Kod rimskih brojeva, cjelobrojno dijeljenje s dva provodimo tako da umjesto dvije iste znamenke zapišemo samo jednu. Ako ne postoje dvije iste znamenke, veću znamenku zapišemo pomoću manjih kako bismo dobili potrebne parove znamenki. Konačno, ako imamo ostatak 1 kod zamjene parova znamenki II, njega ignoriramo, tj. ne pišemo.

Tako na primjer, broj XXIIII (24) nakon dijeljenja s dva prelazi u broj XII (12).

No ako s dva dijelimo broj XVIIII (19) tada prvo znamenku X zapišemo kao VIIIII i potom provodimo zamjenu parova s po jedim simbolom:

XVIIII = VIIIIIVIIII = VVIIIIIIIII  što nakon dijeljenja s dva prelazi u VIIII, odnosno 9.

U ovom primjeru smo jedan par VV zamijenili s V, četiri para II smo zamijenili s četiri znamenke I, a posljednju znamenku I (ostatak) smo ignorirali.

Dakle, rimski brojevi zadovoljavaju tri osnovne pretpostavke potrebne za algoritam egipatskog množenja, pri čemu su postupci koje provodimo više vizualni (dupliranje znamenki, odnosno zamjena parova s jednim simbolom) nego li aritmetički (izuzev dekonstrukcije većih znamenki u manje, odnosno konstrukcije većih znamenki iz manjih). Samim izostankom aritmetike i višeg stupnja apstrakcije te svođenjem postupka na vizualne operacije, postupak je jednostavniji za needuciranog korisnika.

Posvetimo se sad algoritmu egipatskog množenja, koji ćemo paralelno provesti na primjeru množenja brojeva XII (12) i XVII (17), što znači da trebamo dobiti rezultat CCIIII (204).

Formirat ćemo dva stupca: prvome se na vrhu nalazi množitelj, a drugome množenik. U prvom stupcu ćemo broj u svakom koraku cjelobrojno dijeliti s dva, a u drugom stupcu ćemo broj u svakom koraku množiti s dva. U sljedećoj tablici prikazani su ti stupci za brojeve 12 i 17, paralelno u rimskom i dekadskom zapisu.

XII	XVII		12	17
VI	XXXIIII		6	34
III	LXVIII		3	68
I	CXXXVI		1	136

Formiranje stupaca za egipatsko množenje.

Potom u formiranim stupcima prekrižimo sve redove u kojima je u prvom stupcu paran broj. U našem slučaju moramo prekrižiti prvi i drugi red, zato jer su brojevi XII i VI parni (imaju paran broj znamenki V i I).

XII	XVII		12	17
VI	XXXIIII		6	34
III	LXVIII		3	68
I	CXXXVI		1	136

Određivanje sumanada u egipatskom množenju.

Konačno, u drugom stupcu zbrojimo sve preostale neprekrižene brojeve. Taj je zbroj jednak umnošku koji tražimo. Uistinu:

LXVIII+CXXXVI = LXVIIICXXXVI = CLXXXXVVIIII = CLXXXXXIIII =CCIIII,

Odnosno 68 + 136 = 204.

Veliko je pitanje jesu li Europljani Srednjeg vijeka, Rimljani ili pak stari Egipćani razumjeli ili znali objasniti zašto ta metoda funkcionira (kao kontekst za navedeno pitanje predlažem tekst Željka Ivankovića „Je li matematika Zapada superiorna matematici Istoka?“). Iz današnje perspektive odgovor relativno jednostavno slijedi iz svojstva brojeva zapisanih u – binarnom brojevnom sustavu.

Kako bismo to objasnili, vratimo se prethodnom primjeru množenja. Drugi broj u umnošku (broj 17) zapravo nije presudan, pa ćemo ga označiti jednostavno sa x. No prvi broj u umnošku ćemo zato zapisati u binarnom obliku:

\(\small (12)_{10} = (1100)_2 = 1 \cdot 2^3 + 1 \cdot 2^2 + 0 \cdot 2^1 + 0 \cdot 2^0\).

Promotrimo što se točno događa kada broj 12 u binarnom zapisu množimo s brojem x:

\(\small (1100)_2 \cdot x = \left(1 \cdot 2^3 + 1 \cdot 2^2 + 0 \cdot 2^1 + 0 \cdot 2^0\right) \cdot x\)

\(\small = 2^3 \cdot x + 2^2 \cdot x\)

Dakle, kako bismo dobili traženi umnožak, broj  smo tri puta pomnožili s dva i zbrojili ga s vrijednošću koju dobijemo kada  dva puta pomnožimo s dva. No to su iste vrijednosti koje zbrajamo i u postupku egipatskog množenja!

To nije koincidencija. Redove koje zbrajamo smo izabrali kao redove s neparnim brojevima u seriji brojeva u prvom stupcu. Ti brojevi pri dijeljenju s dva imaju ostatak 1, odnosno upravo su te pozicije u binarnom zapisu jednake 1 – budući da se i klasična metoda pretvaranja dekadskog zapisa u binarni provodi formiranjem slične tablice.

Kratko rečeno, algoritam egipatskog množenja paralelno provodi prevođenje prvog faktora u binarni zapis i množenje odgovarajućih potencija broja dva s drugim faktorom. Stari Egipćani ni Rimljani to sigurno ne bi opisali na takav način, budući da binarni brojevni sustav prvi put susrećemo tek u 17. stoljeću u radovima Gottfrieda Wilhelma Leibniza. No činjenica ostaje da su Egipćani, pa potom i Rimljani i Europljani Srednjeg vijeka koristili točan algoritam za određivanje umnoška koji nije ovisio o načinu zapisa brojeva, pa se jednako upotrebljavao u egipatskom i u rimskom brojevnom sustavu.

­­

­Množenje prirodnih brojeva u binarnom brojevnom sustavu: 12 · 13 = 156.

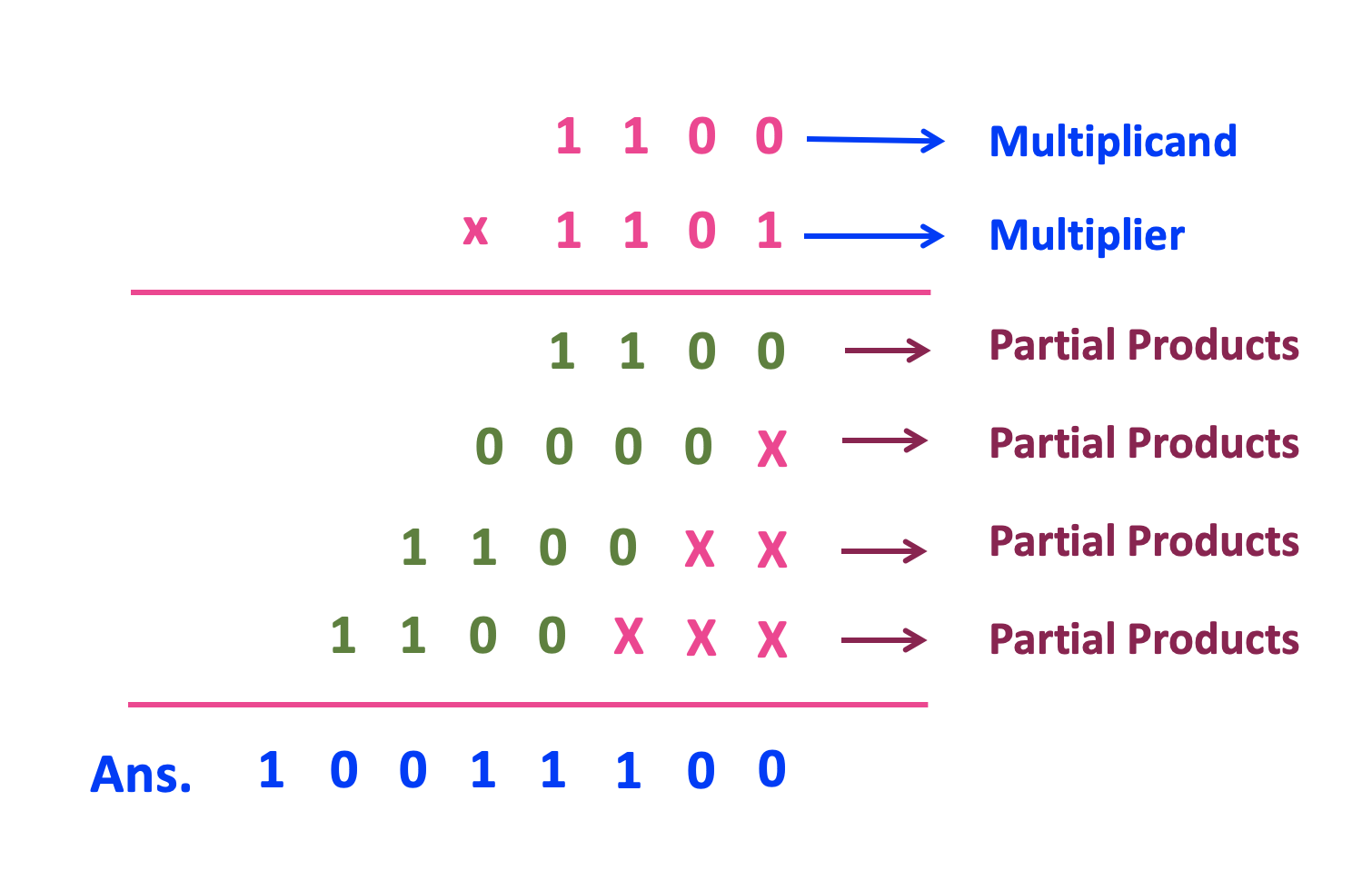
Štoviše, isti algoritam se danas koristi u računalu prilikom množenja dva prirodna broja: množenje desnog broja s dva zapravo znači dodavanje nule s desne strane (odnosno pomak broja u lijevo za jedno mjesto), dok se zbrajaju samo oni brojevi (pomaci) koji odgovaraju poziciji znamenki 1 u binarnom zapisu prvog broja. Na neki način, mogli bismo reći da smo zatvorili puni krug, od egipatskog množenja hijeroglifa do istoga algoritma u modernim računalima.

Za ovu je raspravu presudno istaknuti jednostavnost opisanog procesa. Za množenje dva prirodna broja u rimskom brojevnom sustavu potrebno je znati množiti i dijeliti s dva (što su, pokazali smo, procesi uglavnom vizualnog karaktera), zbrajati (što kod rimskih brojeva znači spajati i preslagivati) i prepoznati neparne brojeve.

Indo-arapski brojevni sustav s druge strane zahtjeva puno veće predznanje. Korisnik mora upotrijebiti više razine apstrakcije (pozicijsko značenje mjesta i prenošenje vrijednosti), te puno veći broj informacija o interakciji znamenki kako kod zbrajanja, tako i kod množenja.

Upravo zbog toga se egipatsko množenje često nazivalo i seljačkim množenjem; jednostavnost i mali broj pretpostavki omogućavao je njegovo korištenje ljudima sa slabim ili gotovo nikakvim obrazovanjem.

Razumno je stoga zaključiti kako su upravo te karakteristike rimskog brojevnog sustava utjecale na njegovu višestoljetnu otpornost u odnosu na, tada, novi indo-arapski brojevni sustav. Neosporna je činjenica da rimski brojevi nisu omogućavali daljnji razvoj matematike, no isto tako, teško je osporiti tvrdnju da su, s obzirom na razinu educiranosti u širokim slojevima stanovništva, rimski brojevi i pripadne operacije predstavljale najbolji omjer uloženog (vremena u široku edukaciju) i dobivenog (jednostavnog provođenja osnovnih aritmetičkih operacija).[2]

• Bilješke

[1] U kasnijim razdobljima, na kraju bi još zapisali pokrate XL (za XXXX) i IV (za IIII), no ta dodatna razina komplikacije zapisa i nije originalno postojala u rimskom brojevnom sustavu.

[2] Istaknimo da se za cjelobrojno dijeljenje prirodnih brojeva u rimskom brojevnom sustavu također koristio prilično efikasan algoritam koji je bio sličan algoritmu za množenje.