Kako je manje ispravna metoda zamijenila puno ispravniju. Laplace vs. Fisher.

Statističari s kraja 19. i s početka 20. stoljeća počeli su insistirati da se vjerojatnosti moraju shvaćati isključivo kao granične frekvencije u tzv. slučajnim eksperimentima, piše Zvonimir Šikić. Rezultat je bila Fisherova metoda, iako nema razloga da se ne upotrebljava generalna, precizna i matematička Laplaceova, tj. bejesovska metoda

• Naslovna ilustracija: Pierre-Simon Laplace, francuski matematičar, fizičar i astronom, kojeg bi danas zvali bejesovcem. (Creative Commons)

• Prethodni članci: Klasična vjerojatnost i primjeri povijesnog razvoja, Vjerojatnost kao frekvencija, Vjerojatnost kao stupanj plauzibilnosti. Matematički temelji bejesovske teorije

Kako odrediti vjerojatnost nekog događaja? Na primjer, vjerojatnost da je rezultat bacanja kovanice glava. Ako o kovanici ne znamo ništa vjerojatnost može biti bilo što između  g = 0 i g = 1 (između ta dva ekstrema leži i slučaj „poštene“ kovanice g = 1/2).

Naivni način rješavanja tog problema je da vjerojatnost identificiramo s relativnom frekvencijom. Kovanicu bacimo 12 puta pa ako je 3 puta pala glava zaključimo da je g = 3/12 = 1/4. To je naivno, jer i „poštena“ kovanica s g = 1/2 može u 12 bacanja dati 3 glave.

• Fisherova metoda

Dakle, kako na temelju obavljenog eksperimenta, 3 glave u 12 bacanja, procijeniti vjerojatnost glave? To današnja školska statistika čini metodom testiranja hipoteza koju je Fisher uveo 1925. Na primjer, ako je hipoteza da je g = 1/2, test se provodi na sljedeći način:

1. Provedemo eksperiment, tj. kovanicu bacimo unaprijed zadani broj puta, na primjer 12 puta.
2. Odredimo prostor mogućih ishoda tog eksperimenta. U našem slučaju to je 2¹² nizova glava i pisama duljine 12. Rezultat eksperimenta jedan je od tih ishoda, npr. PPGPPPGGPPPP.
3. Rezultat eksperimenta sažmemo u jedan numerički podatak, npr. u broj glava koje se pojavljuju u ishodu eksperimenta. Taj sažeti podatak o rezultatu eksperimenta zove se statistika testa. U našem primjeru ta je statistika broj 3.
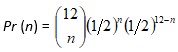4. Izračunamo vjerojatnosti svih mogućih statistika testa, pod uvjetom da vrijedi naša hipoteza, koja se naziva nul-hipotezom. (Podsjetimo se, naša je nul-hipoteza da je kovanica „poštena“, tj. da je g = 1/2.) Sve te vjerojatnosti , gdje je n broj glava u ishodu, čine razdiobu uzorka:

n	Pr (n)	n	Pr (n)	n	Pr (n)	n	Pr (n)
0	0.0001441406	3	0.053710938	6	0.225585938	9	0.053710938
1	0.0029296875	4	0.120849609	7	0.193359375	10	0.0161132813
2	0.0161132813	5	0.193359375	8	0.120849609	11	0.0029296875
						12	0.0001441406

5. Pogledamo rezultate koji su se mogli pojaviti, a koji su uz našu nul-hipotezu ekstremniji od rezultata koji se uistinu pojavio (to su rezultati čija je vjerojatnost manja ili jednaka vjerojatnosti rezultata koji se stvarno pojavio). Izračunamo vjerojatnost pr* da dođe do takvog ekstremnog rezultata. U našem se primjeru stvarno pojavilo n = 3 glave, u 12 bacanja, pa su „ekstremni rezultati“ n = 0,1,2,3,9,10,11,12. To su zatamnjene vrijednosti u gornjoj razdiobi uzorka. Dakle, pr* je zbroj svih zatamnjenih vrijednosti, tj. pr* = 0.15.
6. Nul-hipoteza se odbacuje ako je pr* < 0.05. Dakle, naša nul-hipoteza o „poštenoj“ kovanici nije odbačena našim eksperimentom.

Neki statističari preporučuju 0.01 ili čak 0.001 kao kritičnu vjerojatnost pr*. Prihvaćena kritična vjerojatnost zove se razinom signifikantnosti testa, a za nul-hipotezu se kaže da je odbačena na toj razini signifikantnosti, ako je pr* manja ili jednaka prihvaćenoj kritičnoj vjerojatnosti. Razmislimo što znači da je „nul-hipoteza odbačena na nekoj razini signifikantnosti“. To znači da je rezultat eksperimenta pao u određeno područje, koje je proglašeno „područjem odbacivanja“.

Što to govori o nul-hipotezi? Danas standardno gledište koje je uveo Jerzy Neyman 1930. pretpostavlja da odbacivanje ili neodbacivanje nul-hipoteze nije nikakav matematički pa čak ni induktivni zaključak, nego je tek „instrukcija o induktivnom ponašanju“. Ako se, uz razinu signifikantnosti 0.01, ponašamo prema toj instrukciji onda ćemo, u prosjeku (na duge staze), istinitu hipotezu odbaciti, tj. učiniti ćemo grešku I. tipa, ne više od jednom u 100 puta.

Ključni je problem metode Ronalda Fishera (lijevo) što evaluira samo jednu hipotezu, nul-hipotezu. Jerzy Neyman (desno) smatra kako odbacivanje ili neodbacivanje nul-hipoteze nije nikakav matematički zaključak, nego tek „instrukcija o induktivnom ponašanju“. (Creative Commons)

Možemo se brinuti i o prihvaćanju neistinite hipoteze, tj. o greškama II. tipa, koje  razmatraju Neyman i Pearson 1933. Vjerojatnost greške II. tipa je vjerojatnost odbacivanja istinite alternativne hipoteze H_a, prihvaćanjem neistinite nul-hipoteze H₀. Komplement razine signifikantnosti odbacivanja  hipoteze H_a zove se snagom testa (dok se, u tom kontekstu, razina signifikantnosti odbacivanja nul-hipoteze H₀ zove veličinom testa). Idealno bismo trebali maksimizirati snagu i minimizirati veličinu testa. No, taj je ideal nekonzistentan. Smanjenje veličine testa nosi sobom povećanje njegove snage i obratno.

Osim proizvoljnosti određenja „područja odbacivanja“, nekonzistentnosti redukcije veličine i ekspanzije snage testa, te ispitivanja samo jedne hipoteze, Fisherova metoda ima i drugih problema. Na primjer, različito odabrane statistike testa mogu iz istog eksperimentalnog rezultata izvesti različite zaključke. To je zloglasni problem „izbora statistike“. Tu je i problem „pravila zaustavljanja“. Razmislimo opet o kovanici bačenoj 12 puta, s ishodom koji sadrži 3 glave i 9 pisama. Gore opisani test ne možemo ni početi primjenjivati ako ne znamo je li eksperimentator planirao kovanicu baciti točno 12 puta. Što ako ju je planirao bacati do pojave 3 glave ili dok mu ne dosadi bacanje? Tada prostor mogućih ishoda iz 2. koraka izgleda drukčije, a s time i svi preostali koraci, pa i konačni zaključak. Sama činjenica da su se u 12 bacanja pojavile 3 glave nije dovoljna. Moramo znati kakav smo eksperiment pri tome zamišljali.

I naravno, ključni problem Fisherove metode je da evaluira samo jednu hipotezu, tzv. nul-hipotezu (u našem primjeru „poštenje kovanice“), uzimajući u obzir sve rezultate eksperimenta koji su se mogli desiti. A nas zapravo zanima evaluacija svih mogućih hipoteza, na temelju jednog jedinog rezultata eksperimenta, koji se stvarno desio.

• Laplaceova (bejesovska) metoda

Metodu koja evaluira ono što nas zanima uveo je Laplace, davno prije Ronalda Fishera. Ona je bitno jednostavnija, informativnija i matematički objašnjiva. Najprije ćemo pokazati kako se njome rješava naš problem testiranja kovanice, a zatim ćemo objasniti zašto ju je zamijenila složenija, neinformativnija i matematički neobjašnjiva Fisherova metoda.

Laplacea bismo danas zvali bejesovcem. On bi problem kovanice rješavao primjenjujući Bayesov formulu koju možemo jednostavno izraziti (v. prvi članak o klasičnoj vjerojatnosti) sa „posterior je proporcionalan umnošku priora i pouzdanosti“:

U slučaju da imamo kontinuirano mnogo hipoteza g (kakav je naš slučaj u kojem vjerojatnost glave može biti bilo koja vrijednost g ∈ [0,1])) najčešće je Pr (g) = Pr (g |D) = 0, za svaku pojedinu hipotezu g. Vjerojatnosti različite od 0 imaju intervali oko g, a ne sam g. Te su vjerojatnosti, za dani g, najčešće proporcionalne s duljinama tih intervala dg. Dakle, konstanta proporcionalnosti varira s g i zove se gustoćom vjerojatnosti od g i ako je označimo s pr (g) onda slijedi da je Pr (g ∈ dg) = pr (g) dg; v. sliku.

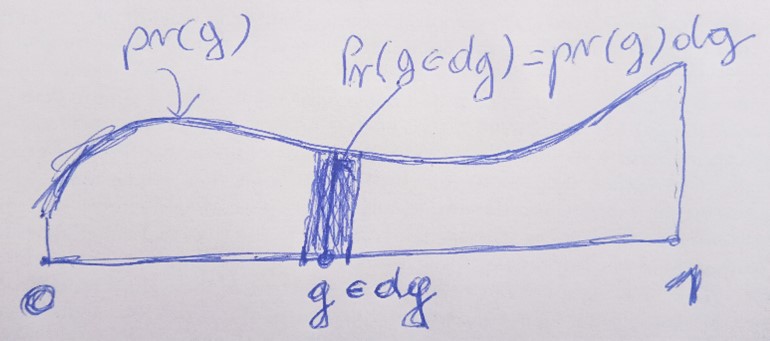
Naravno, isto vrijedi i za Pr (g ∈ dg | DJ). Uvrstimo li sve to u Bayesovu formulu nalazimo:

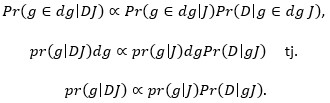
gdje ∝ znači „proporcionalno je“. Dakle, vjerojatnost Pr (g|DJ) koja je vjerojatnost da vjerojatnost glave iznosi g, uz uvjet poznatog podatka D (u našem slučaju, pale su 3 glave u 12 bacanja) i općih informacija J (u našem slučaju, kovanica je bačena visoko, na podlogu koja je ravna, itd.), proporcionalna je umnošku apriorne gustoće vjerojatnosti pr (g|J) i vjerojatnosti Pr (D|gJ) koja je lako izračunljiva (u našem slučaju to je vjerojatnost da se 3 glave pojave u 12 bacanja uz uvjet da vjerojatnost glave iznosi g).

Gustoća vjerojatnosti pr (g|J) je apriorna vjerojatnost  ili  prior i ona daje procjenu vjerojatnosti pr (g|J) dg da je vjerojatnost glave u intervalu dg oko g, prije nego je dostupan rezultat eksperimenta D. Aposteriorna gustoća vjerojatnosti ili posterior pr(g|DJ) izračunava se množenjem priora s lako izračunljivom vjerojatnosti Pr (D|gJ) koja se naziva vjerodostojnost.

Ako nemamo nikakvog razloga da preferiramo bilo koju vrijednost g ∈ [0,1], onda je prior pr (g|J) uniformno distribuiran:

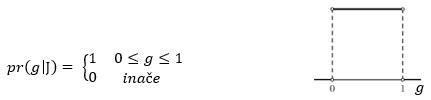
Vjerodostojnost je lako izračunati, Pr (D|gJ) = g ⁿ  (1-g) ^N-n, gdje je g vjerojatnost glave, a n broj glava u N bacanja. Posterior, prema Bayesovu teoremu, nalazimo množenjem:

Dakle, bacimo li kovanicu jednom i padne li glava, posterior je:

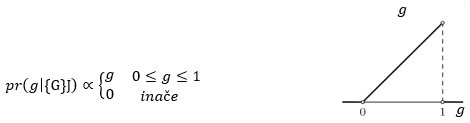
Bacimo li kovanicu još jednom i padne li opet glava, posterior je:

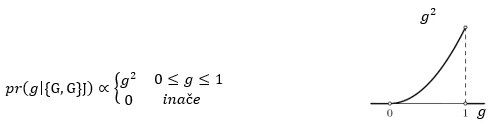
Padne li treći put pismo, posterior je:

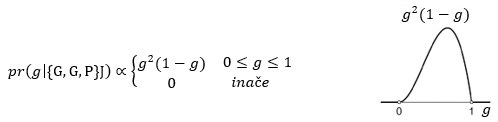
Još jedno pismo i posterior je:

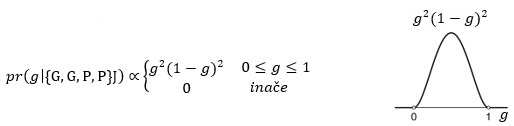
I tako dalje.

Sljedeće slike pokazuju kako se posterior mijenja sa sve više i više podataka o rezultatima bacanja kovanice. Položaj maksimalne vjerojatnosti sve se više stabilizira što je broj podataka veći. Osim toga, sa sve većim brojem podataka graf posteriora postaje sve uži i uži. Nakon 1000 bacanja vjerojatnost da vjerojatnost glave iznosi 1/4 daleko je najveća. Primijetite da smo za svaki g ∈ [0,1] izračunali gustoću vjerojatnosti toga g.

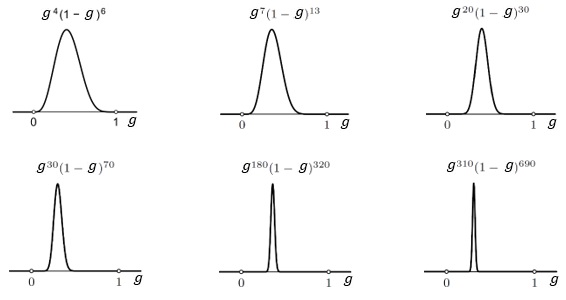
Ljudi bez problema prihvaćaju da je vjerodostojnost Pr (D|gJ) = g ⁿ  (1-g) ^{N- n} , ali imaju rezerve prema prioru. Pitaju se što će biti ako krenemo od nekog drugog priora, a ne od uniformno distribuiranog. No, vidjeli bismo da bi rezultat bio isti. Naš prior, tj. naše preduvjerenje o kovanici, u početku snažno utječe na posterior (ako ste uvjereni da je kovanica „poštena“, tj. da je  g = 1/2, onda vas 3 glave u 12 bacanja neće pokolebati), no kako broj bacanja raste rezultati bacanja nadjačaju sva preduvjerenja (oko 30 000 glava u 120 000 bacanja, pokolebati će vašu vjeru u g = 1/2). To je intuitivno jasno, a matematički slijedi iz Bayesovog teorema.

Primijetimo još jednom, da za razliku od Fisherove metode koja je odbacila ili nije odbacila samo jednu hipotezu (npr. hipotezu da je g = 1/2), Laplaceova metoda daje gustoću vjerojatnosti za svaki g, dakle za svaku moguću hipotezu. Točno smo to htjeli.

• Zašto uopće Fisherova metoda?

Kako je uopće došlo do toga da je Fisherova ograničena, neprecizna i nematematička metoda zamijenila Laplaceovu generalnu, preciznu i matematičku metodu?

Laplaceova bejesovska metoda temelji se na tome da su vjerojatnosti racionalne procjene uvjerenja koje se temelje na raspoloživim podacima. Kao što smo već objašnjavali, nije odmah jasno zašto bi tako shvaćene vjerojatnosti zadovoljavale uobičajene aksiome vjerojatnosti, koje su Laplace i njegovi sljedbenici slobodno koristili. Ako vjerojatnosti shvatimo kao granične frekvencije, vidjeli smo da je te aksiome lako dokazati (iako je sam pojam granične frekvencije nekonzistentan).

Coxov teorem dokazao je da vjerojatnost shvaćena kao „racionalna procjena uvjerenja koje se temelji na raspoloživim podacima“ zadovoljava uobičajene aksiome vjerojatnosti. (American Institute of Physics)

Kako bilo, statističari s kraja 19. i s početka 20. stoljeća počeli su insistirati da se vjerojatnosti moraju shvaćati isključivo kao granične frekvencije u tzv. slučajnim eksperimentima. Nažalost, takvo shvaćanje vjerojatnost hipoteze čini nelegitimnim pojmom: hipoteza je istinita ili lažna, a ne nešto što može biti manje ili više vjerojatno. Dakle, g = 1/2 ili g ≠ 1/2 i nema smisla govoriti o vjerojatnosti od g = 1/2, tj. o Pr (g = 1/2), koja je temelj Laplaceovog pristupa. Rezultat je bila Fisherova metoda.

No, kao što smo objasnili u trećem članku o vjerojatnosti kao plauzibilnosti od 50-tih godina 20. stoljeća znamo da vjerojatnost kao „racionalna procjena uvjerenja koje se temelji na raspoloživim podacima“ zadovoljava uobičajene aksiome vjerojatnosti. To je dokazano Coxovim teoremom i više nema razloga  da ograničenu, nepreciznu i nematematičku Fisherovu metodu upotrebljavamo umjesto generalne, precizne i matematičke Laplaceove, tj. bejesovske metode.