Očekivanje u vjerojatnosti. Petrogradski paradoks i problem dvije omotnice

U 5. nastavku svojeg serijala o vjerojatnosti Zvonimir Šikić objašnjava koji su najbolji prediktori ovisno o tome zanima li nas jesmo li u pravu ili ne, ili koliko griješimo u apsolutnom ili kvadratnom iznosu. Šikić iznosi i dva poznata paradoksa - petrogradski i paradoks dvije omotnice - i detaljno pojašnjava njihove mehanizme.

• Naslovna ilustracija: Nicolaus Bernoulli, švicarski matematičar koji je formulirao petrogradski paradoks. (Creative Commons)

• Prethodni članci: Kako je manje ispravna metoda zamijenila puno ispravniju. Laplace vs. Fisher, Klasična vjerojatnost i primjeri povijesnog razvoja, Vjerojatnost kao frekvencija, Vjerojatnost kao stupanj plauzibilnosti. Matematički temelji bejesovske teorije

Vaše očekivanje E (X), nepoznatog broja X, težinski je prosjek brojeva za koje mislite da bi X mogao biti, s njihovim vjerojatnostima kao težinskim koeficijentima. Zato za slučajni pokus čiji su mogući numerički ishodi X = x₁, …, x_n, a njima odgovarajuće vjerojatnosti p₁, …, p_n, očekivanje od X definiramo kao

(1)                         E (X) = p₁ x₁ + … + p_n x_n.

X zovemo slučajnom varijablom s vrijednostima x₁, …, x_n i odgovarajućim vjerojatnostima p₁, …, p_n.

Najvažnije svojstvo očekivanja je njegova aditivnost (koju je lako dokazati):

E (X + Y) = E (X) + E (Y).

Ako o distribuciji vjerojatnosti slučajne varijable X mislite kao o distribuciji masa onda očekivanje od X možete zamišljati kao težište te distribucije. Naime, ako histogram te distribucije zamislite kao homogenu materijalnu ploču koju balansirate u točkama njene baze onda je točka balansa očekivanje od X.

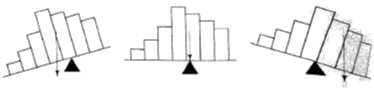
E (X) je točka balansa histograma od X.

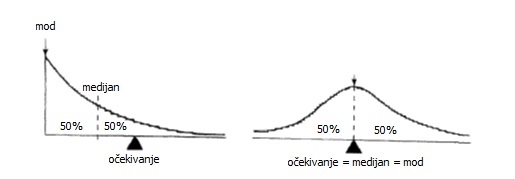
Očekivanje slučajne varijable X tek je jedna, iako najvažnija, „srednja vrijednost“ od X. Primjeri drugih su mod i medijan. Mod je najvjerojatnija vrijednost od X i može ih biti više (npr. sve vrijednosti uniformno distribuirane slučajne varijable njeni su modovi). Medijan je ona vrijednost m koja „X dijeli na pola“, tj. Pr (X ≤ m) i Pr (X ≥ m) su najmanje 50%. Medijan može, ali ne mora, biti jedinstven (npr. sve vrijednosti između 3 i 4 medijani su slučajne varijable čije su vrijednosti iznosi na bačenoj kocki). No, ako distribucija vjerojatnosti od X ima jedinstveni mod i simetrična je oko neke vrijednosti m onda su sve tri „sredine“ jednake toj vrijednosti m.

1. problem. Koliki je očekivani dobitak na ruletu, za uloženi 1 €?

Rješenje. Ako se kladite na jedan od 36 brojeva (na 0 se ne možete kladiti) vjerojatnost da dobijete 35 € (36 dobivenih minus jedan uloženi) je 1/37, a vjerojatnost da „dobijete“ -1 € je 36/37. Dakle, vaša očekivana dobit je

35 € · 1/37 + (-1) € · 36/37 = -1/37 € ≈ -0.027 €.

Ako se kladite na „crveno“ vjerojatnost da dobijete 1 € (dva dobivena eura minus jedan uloženi) je 18/37, a vjerojatnost da „dobijete“ -1 € je 19/37. Dakle, vaša očekivana dobit je

1 € · 18/37 + (-1) € · 19/37 = 1/37 € ≈ -0.027 €.

Ako se kladite na „trećinu“ vjerojatnost da dobijete 2 € (tri dobivena eura minus jedan uloženi) je 12/37, a vjerojatnost da „dobijete“ -1 € je 25/37. Dakle, vaša očekivana dobit je

2 € · 12/37 + (-1) € · 25/37= 1/37 € ≈ -0.027 €.

Na što god se kladite, svaki uloženi euro kockarnici donosi dobitak od cca 2.7 centa, a vama gubitak od cca 2.7 centa. (Američki rulet ima dvije 0 pa tamo svaki uloženi euro kockarnici donosi dobitak od 2/38 €, što je cca 5.3 centa , a vama gubitak od cca 5.3 centa).

2. problem. Koliki je očekivani rezultat bacanja kocke za koju je X = 1, …, 6, ako su vjerojatnosti tih ishoda a) sve 1/6, b) p₁, …, p₆? Koliki je prosjek brojeva dobivenih u velikom broju bacanja?

Rješenje.

a) E (X) = 1/6 + 2/6 +3/6 +4/6 +5/6 + 6/6 = 3.5. Ne možemo očekivati da će jedno bacanje kocke dati 3.5. No, prosjek u velikom broju bacanja bit će približno 3.5. Naime, udjeli pojedinih brojeva u tom dugom nizu bacanja aproksimiraju njihove vjerojatnosti pa je u dugom nizu bacanja

(zbroj bacanja) / (broj bacanja) = (1 · (broj 1-ca) + … + 6 · (broj 6-ica)) / (broj bacanja)

= 1 · udio 1-ca + … + 6 · udio 6-ca ≈ 1 · 1/6 + … + 6 · 1/6  = 3.5 .

b) Analogno, E (X) = 1p₁ + 2p₂ + 3p₃ + 4p₄ + 5p₅ +  6p₆ i to je očekivani prosjek u velikom broju bacanja.

E (X) je prosjek velikog broja slučajno odabranih vrijednosti slučajne varijable X.

Sljedeći problem jasno upozorava da je veliki broj slučajno odabranih vrijednosti slučajne varijable X ključan za to da njihov prosjek bude očekivana vrijednost od X.

3. problem. U sljedećoj i svakoj daljnjoj godini dionice će s jednakom vjerojatnošću rasti 50% ili padati 40%. Kupio sam tih dionica za 1000 €. Hoću li za četiri godine zaraditi ili izgubiti na tim dionicama?

Rješenje. Brzi odgovor je zaradit ću, jer su šanse za dobitak i gubitak iste, a dobitak je 50% što je više od gubitka koji je 40%. Očekivana vrijednost dobitka potvrđuje taj brzi odgovor. Nakon jedne godine očekivana dobit je

E₁ (D) = ½ 1500 € + ½ 600 € = 1050 € = 1.05 · 1000 €,

tj. očekivana godišnja dobit je 5%. Zato je očekivana dobit nakon četiri godine

E₄ (D) = 1.05⁴ · 1000 € = 1216 €.

Dakle, zaradit ću 216 €.

Ali, mogao sam rezonirati i ovako: u dvije će godine dionice rasti, a u dvije padati (jer su šanse pola pola) pa je očekivana dobit nakon četiri godine

M₄ (D) = 1.5² · 0.6² · 1000 € = 810 €.

Dakle, izgubit ću 190 €.

Malo detaljnija analiza jest da u četiri godine imam 16 jednako vjerojatnih mogućnosti (RPRP znači rast u 1. i 3. godini te pad u 2. i 4. godini itd.):

RRRR = 5063 € = 1000 € · 1.5 · 1.5 · 1.5 · 1.5

RRRP = 2025 € = 1000 € · 1.5 · 1.5 · 1.5 · 0.6

RRPR = 2025 € = 1000 € · 1.5 · 1.5 · 0.6 · 1.5

RPRR = 2025 € = 1000 € · 1.5 · 0.6 · 1.5 · 1.5

PRRR = 2025 € = 1000 € · 0.6 · 1.5 · 1.5 · 1.5

RRPP =   810 € = 1000 € · 1.5 · 1.5 · 0.6 · 0.6

RPRP =   810 € = 1000 € · 1.5 · 0.6 · 1.5 · 0.6

PRRP =   810 € = 1000 € · 0.6 · 1.5  · 1.5 · 0.6

PPRR =   810 € = 1000 € · 0.6 · 0.6 ·1.5 · 1.5

PRPR =   810 € = 1000 € · 0.6 · 1.5  · 0.6 · 1.5

RPPR =   810 € = 1000 € · 1.5 · 0.6 · 0.6 · 1.5

PPPR =   324 € = 1000 € · 0.6 · 0.6 · 0.6 · 1.5

PPRP =   324 € = 1000 € · 0.6 · 0.6 · 1.5 · 0.6

PRPP =   324 € = 1000 € · 0.6 · 1.5 · 0.6 · 0.6

RPPP =   324 € = 1000 € · 1.5 · 0.6 · 0.6 · 0.6

PPPP =  130 €  = 1000 € · 0.6 · 0.6 · 0.6 · 0.6

Svih 16 ishoda (od RRRR do PPPP) jednako su vjerojatni pa mi je očekivani iznos (što već znam):

(5063 + 4 · 2025 + 6 · 810 + 4 · 324 + 1 · 30) € /16 = 1216 €.

Dakle, mogu očekivati dobit od 21,6%, tj. uđem li u taj posao mnogo puta, u prosjeku ću ostvarivati dobit od 21,6%. Čini se da je posao povoljan i da ga je racionalno prihvatiti.

Međutim, očekivana dobit (koja je često alfa i omega u procjeni rizika) zamagljuje drugu važnu činjenicu. Pretpostavimo da je 16000 ljudi ušlo u ovaj posao. Samo će njih cca. 5000 imati neku dobit, dok će njih cca. 11000 biti na gubitku. Naime, od 16 jednako vjerojatnih scenarija njih 5 (od RRRR do PRRR) su dobitnički, a njih čak 11 (od RRPP do PPPP) su gubitnički. Budući da sam u taj posao ušao jednokratno (a ne npr. 16000 puta) moje su šanse da dobijem 5/16 = 31%, dok su mi šanse da izgubim 11/16 = 69%.

Naravno, može me privući mogućnost velikog dobitka od 4063 € na uloženih 1000 €, ali moram biti svjesni da to uključuje rizik od 69:31 da ću izgubiti bar 190 €.

„Očekivana dobit“ i „prosjek“ jednostavne su riječi iza kojih se kriju mnoge zamke. Veliki investitori „u posao ulaze mnogo puta“ pa tako realiziraju sve moguće rezultate sa svim njihovim vjerojatnostima što u prosjeku zaista rezultira s matematičkim očekivanjem. Zato oni  imaju valjane razloge da rizik procjenjuju kroz očekivanu dobit, jer je ona za njih zaista očekivana. Za mene koji „u posao ulazim jednom“ bolja je procjena rizika omjer šansi da dobijem ili izgubim u tom jednom poslu (pogotovo ako si ne mogu priuštiti gubitak). Dakle, kada vam netko ponudi fantastičnu očekivanu dobit od 20% sjetite se da ta ponuda ima i drugu stranu. Na primjer, šanse za dobitak u jednom obrtu toga posla mogu biti tek bijednih 0.1% (ako je dobitak u tih 0.1% dobitnih slučajeva spektakularno velik u odnosu na gubitke u ostalih 99,9% slučajeva).

4. problem. Testiramo bolest čija je učestalost p. Umjesto da uzorke krvi testiramo pojedinačno, razvrstamo ih u grupe od po k uzoraka i pomiješamo po pola krvi iz uzoraka svake grupe. Prvo testiramo te smjese. Ako je smjesa od k uzoraka pozitivna, koristeći preostale polovice uzoraka, pojedinačno testiramo uzorke iz te grupe i ustanovimo koji su pozitivni. Ako je grupa negativna svi su u njoj negativni. Smanjujemo li na taj način broj testova?

Rješenje. Neka je X prosječni broj testova po testiranom iz grupe veličine k. Vjerojatnost da je X = 1/k jest vjerojatnost da su svi u grupi negativni i iznosi (1 – p) ^k. Vjerojatnost da je X = (k + 1)/k jest vjerojatnost da je bar netko u grupi pozitivan i iznosi 1 – (1 – p) ^k. Dakle, očekivani prosječni broj testova po testiranom iz grupe veličine k iznosi

E (X) = (1/k) (1 – p) ^k + (1 + 1/k) (1 – p) ^k = 1 + 1/k – (1 – p) ^k ≈ 1 + 1/k – (1 – pk) = 1/k + pk.

Očekivani prosjek je maksimalan za dE/dk = -1/k² + p = 0 tj. za k = 1 /√p. Tada je očekivani prosječni broj testova po testiranom √p  + p /√p = 2√p . To je manje od 1 za p < 1/4, tj. ako
je učestalost bolesti manja od 25% „grupna metoda“ sigurno smanjuje broj potrebnih testova. Na primjer, za p = 1% nalazimo 2√p = 2√0.01 = 2 0.1 = 20% pa je broj potrebnih testiranja „grupnom metodom“ (s grupama veličine k = 1 /√p = 10) za 80% manji od broja potrebnih testiranja „pojedinačnom“ metodom. Za p = 0.1% nalazimo 2√p = 6% pa je broj potrebnih testiranja „grupnom metodom“ (s grupama veličine k = 1 /√p = 100) za 94% manji od broja testiranja „pojedinačnom“ metodom

5. problem klađenja. Ako za uloženih k dobivate X (gdje je X slučajna varijabla), kolika vam je očekivana dobit nakon n ulaganja? Koja je poštena cijena za klađenje na X?

Rješenje. Nakon n ulaganja dobit vam je D_n = X₁ + … + X_n (gdje je X_i = X, za sve i). Prema aditivnosti očekivana dobit je E (D_n) = E (X₁) + … + E (X_n) = n E (X). Dakle, prosječna dobit po jednom ulaganju je E (X) pa je to poštena cijena klađenja na X.

E (X) je poštena cijena klađenja na X.

No, ima tu i nekih problema.

• Petrogradski paradoks

Pretpostavite da vam netko ponudi da više puta bacate pošteni novčić i da će vam dati 2ⁿ eura, ako je n broj pisama koji se pojavi prije prve glave. Koliko biste bili spremni platiti za ovu ponudu?

Vjerojatnost da ćete dobiti 2ⁿ eura vjerojatnost je niza od n pisama i 1 glave, tj. 1/2ⁿ⁺¹. Dakle, očekivana vrijednost dobitka (u eurima) je

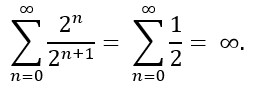
Očekivani iznos nagrade je beskonačan! Stoga se, prema tumačenju očekivane vrijednosti kao “poštene cijene klađenja”, čini da biste za tu ponudu trebali platiti beskonačan iznos. Dakle isplati vam se platiti svaki traženi iznos! Biste li stvarno bili spremni platiti svaki traženi iznos?

Pretpostavimo da je u Petrogradskoj ponudi dogovoreno da će nagrada biti ograničena na 2³⁰ eura. To je nešto više od milijarde eura! Dakle, nagrada će rasti kao u izvornoj ponudi, ali će biti zamrznuta kada prijeđe 2³⁰ eura. Nagrada je sada 2^{min (30,n)}  eura, gdje je n kao i prije. Koliko biste bili spremni platiti za ovu novu ponudu?

Očekivana vrijednost nove nagrade (u eurima) iznosi

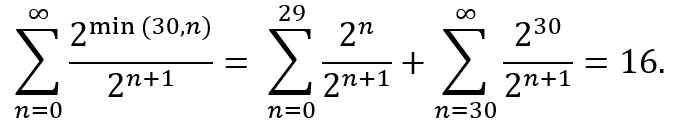
Ograničenje nagrade na milijardu eura mijenja njezinu očekivanu vrijednost s beskonačno na 16 eura! Teorija korisnosti pretpostavlja da svaka osoba ima svoju funkciju korisnosti U (x) koja je količina “korisnosti” (radosti, zadovoljstva i sl.) koju ta osoba doživi ako osvoji x eura. U tom kontekstu, ograničenje ne moramo promatrati kao mijenjanje pravila igre, nego kao funkcija korisnosti oblika U (x) = min(x, 2³⁰). Iskazano riječima, vaša korisnost jednaka je iznosu novca koji dobijete, sve dok ne dosegnete milijardu eura, nakon čega vas više nije briga za novac. Dakle, s ovom funkcijom korisnosti Petrogradska ponuda vama vrijedi samo 16 eura — iako je njena očekivana vrijednost beskonačna.

• Očekivanje i predviđanje

Kako najbolje predvidjeti vrijednost slučajne varijable X? Koji je prediktor najbolji? Da bismo odgovorili na ovo pitanje moramo odrediti što je prediktor. Najjednostavniji prediktor je konstanta c. Koliko je ona dobar prediktor određuje funkcija gubitka G (x, c) čija je vrijednost gubitak koji snosite ako ste predvidjeli X = c, a zapravo je X = x. Dakle, razumno je minimizirati očekivani gubitak E (G (x, c)). Ali sve ovisi o tome što je G (x, c).

6. problem. Pretpostavimo da je G (c, c) = 0, a inače je 1. Dakle, ništa ne gubite ako ste u pravu, a gubite 1 ako ste u krivu (bez obzira koliko ste u krivu). Što je najbolji prediktor slučajne varijable X uz tu pretpostavku?

Rješenje. E (G (x, c)) = 0 · Pr (X = c) + 1 · Pr (X ≠ c) = 1 – Pr (X = c). Taj će očekivani gubitak biti najmanji ako je vjerojatnost Pr (X = c) najveća , tj. najbolji prediktor je vrijednost c čija je vjerojatnost najveća. To je mod koji može, ali ne mora, biti jednoznačno određen.

Ako vas brine samo jeste li u pravu ili ne, najbolji prediktor je mod.

7. problem. Pretpostavimo da je G (x, c) = |x – c|. Dakle, sada gubite to više što više griješite. Što je najbolji prediktor slučajne varijable X uz tu pretpostavku?

Rješenje.

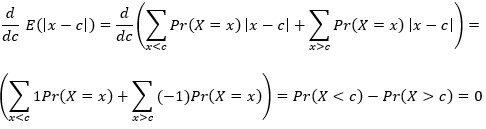
Dakle, Pr⁡ (X < c) = Pr ⁡(X > c)  i najbolji prediktor je vrijednost c koja ima to svojstvo. Ta vrijednost je medijan i može, ali ne mora, biti jednoznačno određena.

Ako vas brine koliko griješite u apsolutnom iznosu, najbolji prediktor je medijan.

8. problem. Pretpostavimo da je G (x, c) = (x – c)². I sada gubite to više što više griješite, ali je funkcija gubitka jednostavnija jer je derivabilna. Što je najbolji prediktor slučajne varijable X uz tu pretpostavku?

Rješenje.

Dakle, c = E(X).

Ako vas brine koliko griješite u kvadratnom iznosu, najbolji prediktor je očekivanje.

I na kraju još dva poučna problema.

• Kapital kompenzira smanjene šanse

Ana i Buba imaju a i b žetona. Koja pobijedi u pojedinoj igri dobije jedan žeton od druge. Prestaju igrati kada jedna od njih ostane bez žetona. Koja je vjerojatnost da Ana osvoji Bubine žetone ako je vjerojatnost njezine pobjede u svakoj pojedinoj igri p?

Rješenje. S A i B označimo vjerojatnosti da Ana odnosno Buba osvoje sve žetone one druge. De Moivreova briljantna ideja bila je da svaki žeton vrednuje tako da očekivana dobit u svakoj pojedinoj igri bude 0. To je postigao vrednovanjem žetona na sljedeći način.

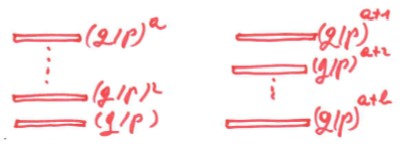
U lijevom stupcu su Anini, a u desnom Bubini žetoni. Uz njih su zapisane njihove vrijednosti (naravno, q = 1 – p). Tko izgubi pojedinu igru, žeton s vrha svojeg stupca prebacuje na vrh protivničkog stupca. Tada je očito

E (dobitak u pojedinoj igri) = p (q/p) ^x+1 – q (q/p) ^x = 0.

Ana će osvojiti sve Bubine žetone vrijedne (q/p) ^a+1 + … + (q/p) ^a+b s vjerojatnošću A, a Buba će osvojiti sve Anine žetone vrijedne (q/p) + … + (q/p) ^a s vjerojatnošću B. Očekivana krajnja dobit Ane je

A [(q/p) ^a+1 + … + (q/p) ^a+b] – B[(q/p) + … + (q/p) ^a] = 0.

To je očekivanje 0, jer je očekivanje u svakoj pojedinoj igri 0, a očekivanje je aditivno. Iz prethodne jednakosti i činjenice da je A + B = 1, lako je izračunati, za p ≠ q:

Za p = q, primjenom identiteta (1 – xⁿ) = (1 – x) (1 + x +x² + … + x^n-1)  lako nalazimo:

Uočimo nadalje da je Anina očekivana dobit u pojedinoj igri 1 · p + (-1) · q = p – q, dok joj je ukupna očekivana dobit Ab – Ba. Slijedi da je očekivani broj igara n = (Ab – Ba) / (p – q). Promotrimo sada neke konkretne slučajeve. Za p = q = ½ i a = 9, b = 1 te a = 90, b = 10 imamo

a	b	p	A	n
9	1	50%	90%	9
90	10	50%	90%	900

Iako je vjerojatnost pobjede u svakoj pojedinoj igri za Anu i Bubu ista, vjerojatnost Anine ukupne pobjedu je velikih 90%, jer u igru ulazi s 9 puta većim kapitalom od Bube. Ako omjer Bubinog i Aninog kapitala ostaje isti, iako se oni proporcionalno uvećavaju, vjerojatnost Anine ukupne pobjede i dalje je 90%. Jedino što Buba može očekivati jest veći broj igara do konačnog poraza (npr. 900 umjesto 9).

Pogledajmo što će se desiti ako vjerojatnost Anine pobjede u pojedinoj igri smanjimo na p = 45%, uz iste iznose početnih kapitala jednakih omjera.

a	b	p	A	n
9	1	45%	79%	11
90	10	45%	13%	766

Uz Bubin početni kapital b = 1, Ana i dalje pobjeđuje uz solidne šanse od 79% i to u malom očekivanom broju od 11 igara. Jedan žeton je premalo da bi se Bubina prednost od q = 55% mogla stvarno realizirati. No, uz Bubin početni kapital b = 10 njena prednost od q = 55% uspješno se realizira i njene šanse da pobijedi rastu s 21% na 87%, bez obzira što je omjer početnih kapitala ostao isti.

Zanimljivo je istražiti za koje početne kapitale a i b su Anine šanse za ukupnu pobjedu veće od Bubinih, čak i kada je Bubina vjerojatnost q, za pobjedu u svakoj pojedinoj igri, veća od Anine vjerojatnosti p. Dakle, za koje a i b je

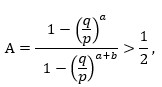
iako je q > p? Ta je nejednakost ekvivalentna nejednakosti:

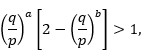
koja je moguće za

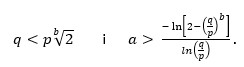
Ako Ana ima neograničene resurse, a Buba ograničene, druga nejednakost sigurno vrijedi pa je za Aninu pobjedu dovoljno da je

Na primjer, za p = 45% i q = 55% Ana će pobijediti, s dovoljno velikim početnim kapitalom a, ako je Bebin početni kapital b < 4, jer je

Za p = 40% i q = 60% Ana će pobijediti, s dovoljno velikim početnim kapitalom a, samo ako je Bebin početni kapital b = 1, jer je

Vjeruje se da je problem dvije omotnice inspirirao belgijski matematičar Maurice Kraitchik, koji je u knjizi La mathematique des jeux (1953.) postavio sličan problem s dva bogataša i dva novčanika u kojima je nepoznat iznos novca. (Wikimedia Commons)

• Problem dvije omotnice

Nudim vam dvije omotnice. U jednoj je dvostruko više novca nego u drugoj. Vi odabirete jednu. Ja vas tada pitam želite li se predomisliti i odabrati drugu. Želite li? Možete i pogledati što je u prvoj.

Recimo da je u prvoj 100 eura. To znači da je u drugoj 50 eura ili 200 eura. Te su alternative jednako vjerojatne, pa je očekivana vrijednost u drugoj omotnici

½ · 200 € + ½ · 50 € = 100 € + 25 €

To je više od 100 eura, koliko je u prvoj omotnici. Dakle, svakako trebate promijeniti svoj prvi odabir. Taj argument vrijedi za svaki iznos x u prvoj omotnici pa niste ni trebali gledati koliko je novca u prvoj omotnici:

1/2 · 2x + 1/2 · x/2 = x + x/4.

Međutim, da ste početno odabrali drugu omotnicu isti bi vas argument uvjeravao da nju trebate promijeniti. Dapače, kada se odlučite za promjenu, isti vas argument uvjerava da trebate ponovo promijeniti (tj. vratiti se početnom odabiru). Tako možete u nedogled. I to je paradoks dvije omotnice.

Kako riješiti taj paradoks? Prije svega, razlikovat ćemo dva problema: POO (problem otvorene omotnice) i PZO (problem zatvorene omotnice). POO vam dopušta da otvorite odabranu omotnicu, pogledate što je u njoj i tek tada odlučite želite li je promijeniti ili ne. PZO zahtjeva da bez otvaranja odabrane omotnice odlučite o njenoj eventualnoj promjeni. Čini se očitim da u PZO nema baš nikakve koristi od promjene odabrane omotnice. Naime, problem je potpuno simetričan u odnosu na odabir jedne ili druge omotnice. POO narušava tu simetriju. Otvaranjem odabrane omotnice dolazite do informacije koja može utjecati na vašu odluku (npr. ako je u njoj 60% dostupnih eura, u drugoj ne može biti 120% dostupnih eura; dostupnih  je najviše 100%).

Da bismo razriješili paradoks pogledajmo još jednom izračun očekivane vrijednosti, na koji se poziva paradoksalna preporuka o zamjeni:

1/2 · 2x + 1/2 · x/2 = x + x/4.

To bi bio korektni izračun očekivane vrijednosti u drugoj omotnici, da sam vam dao omotnicu s x eura i zatim bacanjem novčića odlučio hoću li u drugu omotnicu staviti 2x ili x/2 eura. No, problem nije tako postavljen. Ja sam u omotnice stavio 3y eura (y u jednu i 2y u drugu) i zatim sam vam dao da odaberete jednu od njih. Koju god odaberete vaša je očekivana dobit 3y/2:

1/2 · y + 1/2 · 2y = 3y/2.

Dakle, ako ne otvorite odabranu omotnicu (tj. ako ste u PZO) nema očekivane koristi od zamjene.

Primijetimo da ovaj dio paradoksa zapravo i nema veze s vjerojatnošću. Mogli smo ga formulirati kao „logički paradoks“. Ako je u omotnici koju ste odabrali x onda je u drugoj omotnici 2x ili x/2. Dakle, ako zamjenom dobivate dobit ćete x, a ako zamjenom gubite izgubit ćete x/2. Mogući dobitak veći je od mogućeg gubitka. S druge strane, razlika iznosa u omotnicama je y. To znači da zamjenom dobivate ili gubite y. Mogući dobitak jednak je mogućem gubitku. Dva istaknuta zaključka međusobno se pobijaju i to je, navodno, paradoks. No, već smo objasnili zašto je argument s y valjan, a onaj s x nije.

Jednu od prvih verzija problema dvije omotnice opisao je 1953. i britanski matematičar John Littlewood (lijevo), koji je problem pripisao austrijskom fizičaru Erwinu Schrödingeru (desno). (Wikimedia Commons)

Okrenimo se sada POO-u, koji je zanimljiviji. Što se mijenja ako saznate iznos u odabranoj omotnici; dakle, ako je otvorite? Mogli biste pomisliti: ništa, prethodna analiza vrijedi za svaki y, pa informacija o tome koliki je y nema dodatnu vrijednost. Pomislili biste krivo. (Već i zbog toga što otvaranjem omotnice niste ni saznali koliki je y. Onaj x koji vidite možda je y, a možda je i 2y. No to je problem koji smo već razriješili.)

Da je prva misao pogrešna postat će vam jasno ako razmislite o omotnici u kojoj vidite više od 1/3 meni dostupnih eura. Vjerojatnost većeg iznosa u drugoj omotnici tada je nula i vi (naravno) nećete mijenjati odabranu omotnicu. Ono što vidite u odabranoj omotnici može biti i te kako informativno.

Da biste mogli iskoristiti tu informaciju morali biste znati koliko je vjerojatno da ću ja određeni iznos staviti u omotnicu. Možete se ograničiti na manji iznos y, jer on potpuno determinira veći iznos 2y. Dakle, očekivanu vrijednost u drugoj omotnici možete izračunati samo ako znate kolika je vjerojatnost S (y), da ću ja u omotnicu s manjim iznosom staviti y eura. Ako ste u 1. omotnici našli 100 eura onda je očekivana vrijednost u 2. omotnici:

Pr (O₁ < O₂| O₁ = 100 €) · 200 € + Pr (O₁ > O₂| O₁ = 100 €) · 50 €.

Funkcija S (y), koja proizlazi iz mojih novčanih mogućnosti i navika ili naprosto iz načina na koji punim omotnice, omogućava vam da uz pomoć Bayesove formule izračunate potrebne vjerojatnosti:

Pr (O₁ < O₂ | O₁ = 100 €) = Pr (O₁ < O₂) · Pr (O₁ = 100 € | O₁ < O₂) / Pr (O₁ = 100 €)

= ½ S (100) / ( ½ S (50) + ½ S (100)) = S (100) / (S (50) + S (100)).

Na isti način nalazimo:

Pr (O₁ > O₂|O₁ = 100 €) =  S (50) / (S (50) + S (100)).

Intuitivno, bez poziva na Bayesa, prva vjerojatnost (da je 100 eura koje vidite manji iznos) mora biti proporcionalna sa S (100), tj. s vjerojatnošću da ću ja u manju omotnicu staviti 100 €. Druga vjerojatnost (da je 100 eura koje vidite veći iznos) mora biti proporcionalna sa S (50), tj. s vjerojatnošću da ću ja u manju omotnicu staviti 50 €. No, to su jedine dvije opcije, pa zbroj njihovih vjerojatnosti mora biti 1, tj. Pr (O₁ < O₂ | O₁ = 100 _€) i Pr (O₁ > O₂|O₁ = 100 _€) moraju imati gore izračunate vrijednosti.

Dakle, ako je u 1. omotnici 100 € onda je očekivana vrijednost u 2. omotnici:

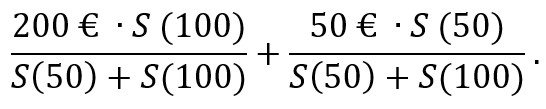
Naravno, to vrijedi i za svaki drugi iznos x. Ako je u 1. omotnici x eura onda je očekivana vrijednost u 2. omotnici:

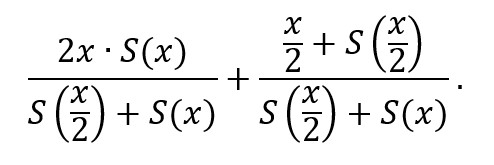
Lako je izračunati da će taj iznos biti veći od x, tj. zamjena će se isplatiti, samo ako je za svaki x:

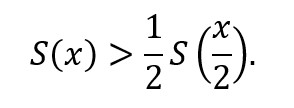
Međutim, ne postoji konačna distribucija vjerojatnosti S koja bi zadovoljavala taj uvjet. (Za one koji znaju nešto više teorije vjerojatnosti napominjemo da i među beskonačnim distribucijama taj uvjet mogu zadovoljiti samo one čije je očekivanje beskonačno. Usput, to su one distribucije za koje ne vrijedi zakon velikih brojeva.)

Rezimirajmo što smo zaključili o POO. Taj problem zapravo nije dobro postavljen. Da biste ga riješili morate znati moj S, tj. morate znati moje novčane mogućnosti i navike ili naprosto način na koji punim omotnice. Bez toga ne možete izračunati očekivani iznos u 2. omotnici. To je analogno sljedećem problemu.

Vozila A i B voze istom cestom u istom smjeru. A vozi 10 km/h brže od B. Koliko su vozila udaljena nakon 1 sata vožnje?

Brzopleti je odgovor 10 km. No, zapravo ne znate odgovor ako ne znate početni položaj vozila, tj. 10 km je točan odgovor samo ako kreću s istog mjesta. Bez te informacije ne možete izračunati traženu udaljenost.

Isto tako ne možete izračunati ni očekivani iznos u 2. omotnici ako ne znate moj S. Teorija vjerojatnosti vam omogućava da iz jednih vjerojatnosti računate druge, ali vam najčešće ne daje početne vjerojatnosti. A od nečega morate početi. (U stručnom žargonu: nema posteriora bez priora.) Problem priora i inače je glavni problem upotrebe teorije vjerojatnosti u analizi podataka (od astronomije preko medicine do ekonomije). Te analize zapravo su kvantifikacije našega znanja o nekom fenomenu na temelju sakupljenih podataka o tom fenomenu. Radi se o računanju uvjetnih vjerojatnosti, a uvjeti su sakupljeni podaci. No, taj račun ovisi i o apriornim vjerojatnostima – što znate nakon što ste sakupili podatke ovisi i o tome što ste znali prije sakupljanja.

Na sreću, u većini znanstvenih primjena, moguće je pokazati da su konačni zaključci neovisni o apriornim vjerojatnostima – od kojih god priora krenete podaci vas vode istim zaključcima (usp. 4. članak u seriji). To su situacije u kojima iz novih podataka saznajemo toliko da oni potpuno brišu sva prethodna znanja o fenomenu koji istražujemo. No, nije uvijek tako i ne treba se slijepo pouzdati u univerzalnu irelevantnost priora. POO je samo jedan primjer problema u kojem je konačni zaključak osjetljiv na priore.

Recimo još nešto o vezi PZO i POO. Ako i ne otvarate odabranu omotnicu lako možete zamisliti da ste je otvorili i da ste u njoj našli x eura pa ako znate moj S možete izračunati očekivanu dobit od zamjene. Budući da samo zamišljate da ste vidjeli x eura, vaša konačna odluka mora se temeljiti na prosjeku svih mogućih dobitaka i gubitaka koje vam donosi zamjena (po svim mogućim vrijednostima x koje distribuira moj S). Nije teško izračunati da je ta srednja vrijednost nula za svaki prihvatljivi S (tj. za svaki S koji ima konačno očekivanje). Dakle, razrješenje POO-a u potpunoj je harmoniji s razrješenjem PZO-a.

I na kraju, zašto neki smatraju da POO nije riješen? Mnogi zato jer ne razumiju rješenje, ali neki imaju i  bolje razloge. Činjenica je da postoje razdiobe S (y) za koje vam korektni izračun očekivane dobiti kaže da omotnicu uvijek trebate zamijeniti. No, to su uvijek razdiobe u kojima ja raspolažem s beskonačnim količinama novca i u kojima je očekivana vrijednost svih y koju stavljam u manju omotnicu također beskonačna.

Na primjer, ako su (manji) iznosi koje stavljam u omotnicu 1, 2, 4, 8, 16, … , 2ⁱ, 2ⁱ⁺¹, … onda će se zamjena isplatiti (usp. gore) ako je za svaki i

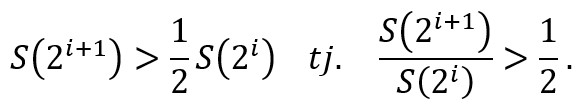
Svaki geometrijski red s kvocijentom q > ½  zadovoljava tu nejednakost. Ako ga još podijelimo s njegovom sumom 1/(1-q) onda će i zbroj vjerojatnosti svih elementarnih ishoda biti 1 (što je nužan uvjet da bi se radilo o razdiobi vjerojatnosti). Dakle, ako je moja razdioba

y	1	2	4	8	…	2i	…
S (y)	(1-q)	q (1-q)	q2 (1-q)	q3 (1-q)	…	qi (1-q)	…

onda uvijek trebate mijenjati i tu se ne radi o nikakvom paradoksu nego o još jednom „paradoksu“ beskonačnosti. Oni se gotovo uvijek svode na to da mislimo kako ono što vrijedi u konačnim slučajevima mora vrijediti i u beskonačnim (npr. da dio uvijek mora biti manji od cjeline, jer to vrijedi za konačne veličine). To naprosto nije istina koliko god se to nekome činilo paradoksalnim.

Osim toga neriješenim problemom ostaje i kako trebate postupiti u slučaju da ne znate moj S, pa stoga ne možete  izračunati očekivanu vrijednost u 2. omotnici. U praksi se uspješnom pokazala strategija slučajnih promjena (s vjerojatnostima koje na određeni način ovise o x). Zanimljivo je da se analogna situacija pojavljuje u vezi s razbijanjem simetrije u kvantnoj fizici, no to prelazi okvire ove serije.