Kauzalna revolucija u vjerojatnosti. Formalne metode tumačenja uzročnosti

Korelacija nije uzročnost i nema čisto probabilističke metode koja uzročnu priču može odrediti samo iz podataka, piše Zvonimir Šikić u svojem posljednjem nastavku serije o vjerojatnosti. Sami podaci nisu dovoljni da se iščita priča, no kauzalne pretpostavke mogu pomoći u pronalaženju varijabli koje treba ili ne treba kontrolirati.

• Naslovna fotografija: Izraelski informatičar i filozof Judea Pearl (Creative Commons)

• Prethodni članci: Problem indukcije i Simpsonov paradoks. Istina skrivena u sub-populacijama, Algoritamske definicije slučajnosti. Nepredvidivost, tipičnost i nekompresibilnost beskonačnih nizova, Proširena logika vjerojatnosti. Počeci i suvremeni kontekst, Očekivanje u vjerojatnosti. Petrogradski paradoks i problem dvije omotnice, Kako je manje ispravna metoda zamijenila puno ispravniju. Laplace vs. Fisher, Klasična vjerojatnost i primjeri povijesnog razvoja, Vjerojatnost kao frekvencija, Vjerojatnost kao stupanj plauzibilnosti. Matematički temelji bejesovske teorije

• Je li istina u populaciji ili je u sub-populacijama

Koju odluku donijeti ako smo suočeni sa Simpsonovim obratom. U cijeloj populaciji vrijedi S, a u obje komplementarne situacije vrijedi –S. Gdje se onda nalazi istina? U cijeloj populaciji ili u sub-populacijama? Promotrimo još jednom primjer s kuglama iz prethodnog nastavka našeg serijala.

Imamo 80 kugli, od kojih je 40 u posudi P1, a  40 ih je u posudi P2. Kugle su crvene ili bijele i velike ili male.

P1	C	B		P2	C	B		P	C	B
V	7	3		V	9	21		V	16	24
M	18	12		M	2	8		M	20	20

Postoci crvenih kugli među malim i velikim kuglama u populaciji i obje sub-populacije izgledaju ovako.

	Crvene među malima	Crvene među velikima
P1	60%	70%
P2	20%	30%
P	50%	40%

Ako želite crvene kugle onda se u sub-populacijama P1 i P2 trebate kladiti na velike kugle a u cijeloj populaciji P na male kugle. U prethodnom nastavku našeg serijala objasnili smo zašto se takav obrat može dogoditi i zašto nas to ne bi trebalo iznenaditi, iako je u suprotnosti sa načelom sigurne stvari STP (sure thing principle).

Međutim, pogledajmo iste podatke u kauzalnom kontekstu. Sada imamo 80 pacijenata, 40 muškaraca i 40 žena (primijetite da su brojke identične onima u primjeru s kuglama).

Ž	O	-O		M	O	-O		P	O	-O
-L	7	3		-L	9	21		-L	16	24
L	18	12		L	2	8		L	20	20

Kontekst je kauzalan jer pretpostavljamo da liječenje uzrokuje ozdravljenje,  u manjoj ili većoj mjeri (za razliku od veličine kugle koja ne uzrokuje njenu boju ni u kojoj mjeri).

Od 10 žena koje nisu liječene, 7 ih je ozdravilo. Od 30 žena koje su liječene, 18 ih je ozdravilo. Stopa oporavka neliječenih žena je 7/10 = 70%. Ona je veća od stope oporavka liječenih žena, koja je 18/30 = 60%. To je prikazano u Ž-tablici.

Od 30 muškaraca koji nisu liječeni, 9 ih je ozdravilo. Od 10 muškaraca koji su liječeni, 2 su ozdravila. Stopa oporavka neliječenih muškaraca je 9/30 = 30%. Ona je veća od stope oporavka liječenih muškaraca, koja je 2/10 = 20%. To je prikazano u M-tablici.

Tablica u kojoj su skupljeni svi pacijenti, i muškarci i žene, nalazi se desno. Od 40 pacijenata koji nisu liječeni, njih 16 je ozdravilo. Od 40 pacijenata koji su liječeni, njih 20 je ozdravilo. Stopa oporavka neliječenih pacijenata je 16/40 = 40% i ona je manja od stope oporavka liječenih pacijenata, koja je 20/40 = 40%. Dakle, u cijeloj populaciji stope su se obrnule. Sve to možemo prikazati u jednoj tablici koja je brojčano identična onoj s kuglama.

	Ozdravili među liječenima	Ozdravili među neliječenima
Ž	60%	70%
M	20%	30%
P	50%	40%

U ovom kauzalnom kontekstu gotovo svi su uvjereni da prava istina leži u sub-populacijama. Ali koji su argumenti za uvjerenje da ono što je istina u sub-populacijama vrijedi i za cijelu populaciju; bez obzira na podatke u cijeloj populaciji? Mogli bismo reći da je intuitivno jasno da ne postoji lijek koji loše djeluje na muškarce i loše djeluje na žene, a dobro djeluje na ljude. Ali na čemu se temelji ta intuicija?

Pearl u svojoj knjizi Causality iz 2000. daje objašnjenje. Pretpostavimo da istražujemo srčane udare. Iz podataka vidimo da se žene bolje oporavljaju i da su sklonije liječenju od muškaraca. Razlog zašto se lijek čini korisnim u cijeloj populaciji je taj što je kod slučajnog odabira liječene osobe veća vjerojatnost da će to biti žena, pa je veća vjerojatnost da će odabrana osoba ozdraviti. Dakle, da bismo procijenili učinkovitost lijeka, moramo usporediti ljude istoga spola, kako bismo osigurali da se razlika u stopama oporavka između onih koji se liječe i onih koji se ne liječe ne može pripisati spolu (umjesto liječenju).

Imajte na umu da sub-populacije ne daju uvijek točan odgovor. Zamislite iste brojke, ali ono što je bio spol pacijenata sada neka bude krvni tlak pacijenata na kraju liječenja. Nadalje, pretpostavite da lijek utječe na oporavak snižavanjem krvnog tlaka. Biste li i sada preporučili lijek? Odgovor opet proizlazi iz načina na koji su podaci generirani. U općoj populaciji lijek poboljšava stope oporavka zbog svog učinka na krvni tlak. Ali u sub-populacijama, NKT i VKT, ne bismo vidjeli taj učinak, jer će se oni s niskim krvnim tlakom oporaviti, a oni s visokim neće, bez obzira jesu li liječeni ili nisu. Budući da je snižavanje krvnog tlaka jedan od mehanizama kojim liječenje utječe na oporavak, podatke nema smisla separirati na temelju krvnog tlaka.

• Kauzalno načelo sigurne stvari

Prethodni argumenti daju odgovor i na Blythovo navodno obaranje načela sigurne stvari. On je predložio dvije oklade:

L oklada:

Slučajno odabirete pacijenta dok ne naiđete na jednog koji uzima lijek i tada se kladite da će se taj pacijent oporaviti.

-L oklada:

Slučajno odabirete pacijenta dok ne naiđete na jednog koji ne uzima lijek i tada se kladite da će se taj pacijent oporaviti.

Ako je odabrani pacijent muškarac, iz podataka slijedi da vam se više isplati -L oklada.

Ako je odabrani pacijent žena, iz podataka opet slijedi da vam se više isplati -L oklada.

Ako ne znate je li odabrani pacijent muškarac ili žena, iz podataka slijedi da vam se više isplati L oklada. To, prema Blythu, obara načelo sigurne stvari.

Međutim, Blythov protuprimjer ne obara kauzalno načelo sigurne stvari koje je eksplicitno formulirao J. Pearl, a implicitno ga je podrazumijevao L. J. Savage i svi mi. Ono glasi ovako:

Akcija L koja povećava vjerojatnost događaja O u obje sub-populacije S i -S povećava vjerojatnost od O i u cijeloj populaciji, pod uvjetom da ta akcija ne utječe na vjerojatnosti sub-populacija.

Naime, kako pokazuju podaci, vjerojatnost da će odabrani L pacijent biti muškarac je 25%, dok je vjerojatnost da će biti žena 75%.

S druge strane, vjerojatnost da će odabrani -L pacijent biti muškarac je 75%, dok je vjerojatnost da će biti žena 25%.

Stoga akcije L i -L utječu na vjerojatnosti sub-populacija odabranih muškaraca i odabranih žena, što je u suprotnosti s uvjetima kauzalnog STP-a.

Primijetite da u izvornom primjeru akcije L = liječi pacijenta i -L = ne liječi pacijenta, ne utječu na mušku i žensku sub-populaciju, jer lijek ne utječe na spol.

Fenomen Willa Rogersa

Možda trebamo dodatno objasniti zašto smo gore napisali da smo „svi mi“ oduvijek implicitno razumjeli  da „akcija ne smije utjecati na vjerojatnost sub-populacija“. Jednostavna potvrda te činjenice jest da šale poput ove Willa Rogersa razumije najšira publika:

Kada se stanovnici Oklahome presele u Kaliforniju prosječna inteligencija poraste u obje države.

Svi razumiju da se prosječna inteligencija može povećati u obje sub-populacije, iako ostaje ista u cijeloj populaciji, ako se sub-populacije mijenjaju migracijom. (Da biste jasno vidjeli vezu sa STP-om, promatrajte migraciju kao akciju, a Oklahomu i Kaliforniju kao sub-populacije.) Naime, ako je inteligencija svakog stanovnika Oklahome viša od prosječne inteligencije stanovnika Kalifornije (što je poanta Rogersove šale) onda je jasno da migracija podiže prosječnu inteligenciju u obje sub-populacije, iako (protivno STP-u) ne mijenja prosječnu inteligenciju u cijeloj populaciji. Razlog je kršenje kauzalne klauzule, jer akcija mijenja relativne veličine sub-populacija, Oklahome i Kalifornije.

U stvarnom životu to susrećemo u medicinskom fenomenu koji se naziva migracija uloga, a koji su opisali Feinstein i suradnici 1985. u članku The Will Rogers phenomenon, stage migration and new diagnostic techniques as a source of misleading statistics for survival in cancer. Povećano dijagnosticiranje bolesti dovodi do prelaska ljudi iz skupine zdravih u skupinu bolesnih ljudi. To rezultira očitim produljenjem životnog vijeka u obje skupine, iako nema povećanja životnog vijeka u ukupnom stanovništva. Važno je razumjeti da se fenomen javlja i kada se ništa ne mijenja u protokolima liječenja.

Paradoksalnost Simpsonovih obrata (?)

No, vratimo se problemu paradoksalnosti Simpsonovih obrata. Definitivno imamo veći problem kada su Simpsonovi obrati u “konfliktu” s kauzalnim STP-om.

U ne-kauzalnom Simpsonovom obratu s kuglama, ako iz sub-populacija želimo dobiti crvenu kuglu, trebamo se kladiti na veliku kuglu, a ako je želimo dobiti iz cijele populacije, trebamo se kladiti na malu. Dakle, trebamo poštivati Simpsonov obrat i tu nema paradoksa.

U kauzalnom Simpsonovom obratu s pacijentima, ako želimo da pacijent ozdravi, naprosto ga trebamo ne liječiti. Dakle, trebamo ignorirati Simpsonov obrat, jer „iako je on tu, zapravo ga ne bi trebalo biti“. To možemo smatrati paradoksalnim, s čime se slaže i Pearl.

No, Pearl ide i korak dalje. On se slaže sa Savageom da se “veoma rijetko odluka donosi na temelju [kauzalnog] STP-a … ali nijedno drugo ne-logičko načelo … ne nailazi na tako spremno prihvaćanje.” Dakle, kauzalni STP je jedinstven u svojoj univerzalnoj prihvaćenosti unatoč činjenici da nije utemeljen ni na logici ni na vjerojatnosti. Zato, pitajući se što je potrebno za potvrdu kauzalnog STP-a, Pearl zapravo želi odgovoriti na pitanje što upravlja ljudskim mišljenjem. Naime, što god pretendira da predstavlja ljudsko razmišljanje mora uključivati kauzalni STP kao teorem. Ukratko, univerzalnost intuicije da ne postoji lijek koji je loš za muškarce, loš za žene i dobar za ljude sugerira da ljudi koriste neku vrstu kauzalnih Bayesovih mreža za predstavljanje i procesuiranje uzročnih odnosa (pa nije ni čudo da se u uzročnom kontekstu Simpsonovi obrati percipiraju kao paradoksi).

Pearl također smatra da su ljudi, kao primarno kauzalna bića, skloni i nekauzalne Simpsonove obrate tumačiti kao kauzalne te da zato i njih ponekad doživljavaju kao paradoksalne. Međutim, mislim da je u nekauzalnom slučaju objašnjenje “popunjavanjem praznina najjednostavnijim pretpostavkama ” češće u igri.

Probabilističko pretjerivanje

R. Jeffrey je 1982. u članku The sure thing principle inzistirao na strožem uvjetu korektne primjene načela sigurne stvari. Zahtijevao je da „akcije i sub-populacije moraju biti stohastički [a ne samo uzročno] nezavisne“. To je tipično za one koji misle da je jedino stohastička nezavisnost jasno definirana, a da kauzalna nezavisnost nije, a možda ni ne može biti jasno definirana. No, time se načelo sigurne stvari svodi na probabilistički zakon, jer jači uvjet garantira Pr (S|U) = Pr (S|-U) = Pr (S) i Pr (-S|U) = Pr (-S|-U) = Pr (-S) pa se standardno probabilističko pravilo totalne vjerojatnosti

Pr (P|U) = Pr (P|U,S) Pr (S|U) + Pr (P|U,-S) Pr (-S|U)

Pr (P|-U) = Pr (P|-U,S) Pr (S|-U) + Pr (P|-U,-S) Pr (-S|-U)

svodi na

Pr (P|U) = Pr (P|U,S) Pr (S) + Pr (P|U,-S) Pr (-S)

Pr (P|-U) = Pr (P|-U,S) Pr (S) + Pr (P|-U,-S) Pr (-S).

Tada iz Pr (P|U,S ) > Pr (P|-U,S) i  Pr (P|U,-S ) > Pr (P|-U,-S) odmah slijedi Pr (P|U) > Pr (P|-U).

No, Jeffreyev uvjet je pretjeran. Njegovo isključivanje svih slučajeva u kojima su sub-populacije i akcije  stohastički ovisne isključio bi istraživanja u kojima pojedinci s određenim karakteristikama (spol, razina obrazovanja i sl.) s većom  vjerojatnošću traže liječenje, što je čest slučaj u opservacijskim istraživanjima. Dovoljno je isključiti samo kauzalne ovisnosti, a dopustiti čisto stohastičke. (Ta se razlika ne može izraziti u jeziku teorije vjerojatnosti što zbunjuje mnoge matematičare i statističare.)

• Kauzalnost i vjerojatnost

Primjena pogrešnog načela „stopa u populaciji jednaka je prosjeku stopa u sub-populacijama“ sigurno je odgovorna za mnoge pogrešne procjene Simpsonovih situacija. No, važnu ulogu u tome ima činjenica da ljudi u nedostatku informacija popunjavaju praznine zdravo razumskim pretpostavkama koje često opravdavaju primjenu tog načela. S druge strane, neke možda složenije pretpostavke dovode do drugih rezultata koji mogu biti u suprotnosti s načelom i to ga čini općenito nevaljanim. To smo već zaključili u prethodnom nastavku ovog serijala.

U prethodnom dijelu ovog nastavka vidjeli smo da su ozbiljniji problemi u kojima je Simpsonov obrat u „sukobu“ s kauzalnim načelom sigurne stvari. Taj bi se „sukob“ mogao nazvati paradoksalnim, jer psihološki ima taj karakter. Vidjeli smo, i to je najvažniji uvid koji nam daju Simpsonovi obrati i kauzalni STP, da se odgovor na pitanje „treba li u obzir uzeti stope u sub-populacijama ili stopu u cijeloj populaciji“ ne nalazi u podacima. Kako bismo odlučili hoće li lijek naštetiti ili pomoći pacijentu, prvo moramo razumjeti „priču“ koja stoji iza podataka, tj. uzročne mehanizme koji su generirali podatke koje vidimo.

Na primjer, iz podataka vidimo da postoji korelacija između spola i liječenja te između spola i oporavka L ⟷ S ⟷ O. Ali iz samih  podataka ne možemo zaključiti da su uzročni odnosi oblika L ← S → O, a samo iz toga možemo zaključiti da moramo kontrolirati varijablu S (tj. da se istina se nalazi u sub-populacijama). Da su uzročni odnosi drukčiji, npr. da su oblika  L → S → O (kao u slučaju krvnoga tlaka) ili L → S ← O, ne bismo smjeli kontrolirati S (tj. istina bi se tada nalazila u cijeloj populaciji).

Kako to ispravno tvrde udžbenici vjerojatnosti i statistike, korelacija nije uzročnost i nema čisto probabilističke metode koja uzročnu priču može odrediti samo iz podataka. Zato istraživači, uz korištenje probabilističkih metoda, podatke najčešće moraju  tumačiti i na temelju neformalnih uzročno-posljedičnih pretpostavki.

Postoje, međutim, i formalne metode koje se mogu koristiti za izražavanje i tumačenje uzročnosti. Uz njihovu pomoć moguće je matematički opisati uzročne scenarije bilo koje složenosti i odgovoriti na probleme donošenja odluka u bitno složenijim situacijama od onih koje generiraju Simpsonovi obrati. Riječ je o formalnoj teoriji kauzalnosti razvijenoj u zadnjih 30-tak godina, koju mnogi smatraju „kauzalnom revolucijom“.

Kauzalna revolucija

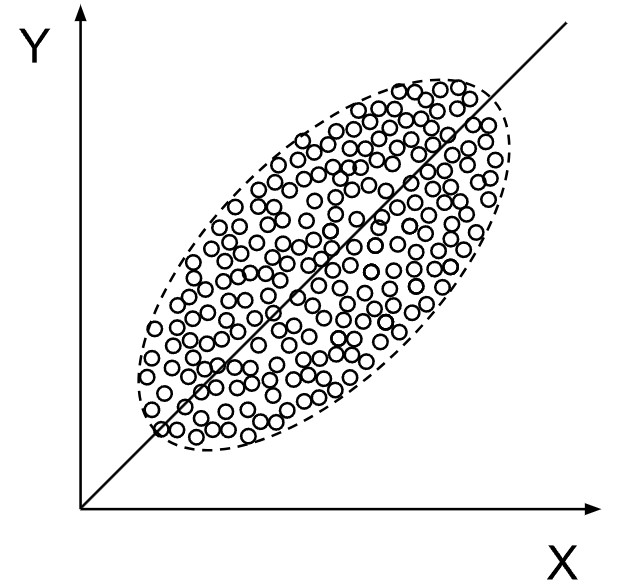
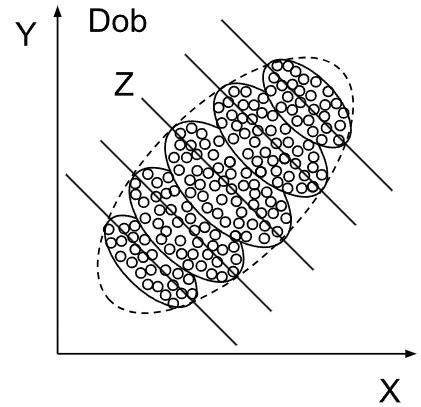
Problem varijabli koje treba ili ne treba kontrolirati zapravo je uvijek prisutan i ne možemo ga riješiti bez kauzalnih pretpostavki. Podaci i odgovarajuće vjerojatnosti nisu dovoljni. Pogledajmo, na primjer, populaciju na slici lijevo, u kojoj svaka individua (točka) ima razinu x svojstva X i razinu y svojstva Y. Očito postoji pozitivna korelacija svojstava X i Y u toj populaciji. No, podijelimo li populaciju na sub-populacije Z kao na slici desno, tada    očito postoji negativna korelacija svojstava X i Y u svakoj od sub-populacija. Samo na temelju podataka ne možemo odlučiti jesu li X i Y korelirani pozitivno ili negativno.

Pretpostavimo da je varijabla Z kauzalno vezana s varijablama X i Y poput rašlji:

X ← Z → Y

Jedan konkretni primjer je:

Veličina cipela ← Dob djeteta → Sposobnost čitanja

U tom slučaju Z kao, zajednički uzrok od X i Y, korelira X i Y iako među njima nema uzročne veze. Ovu lažnu korelaciju možemo eliminirati tako da kontroliramo Z (ako zasebno gledam trogodišnjake, četverogodišnjake, itd. neće biti korelaciju između veličine cipela i sposobnosti čitanja). Dakle, zajednički uzrok uvijek trebamo kontrolirati.

Pretpostavimo da je varijabla Z kauzalno vezana s varijablama X i Y poput lanca:

X → Z → Y

Jedan konkretni primjer je:

Vatra → Dim → Alarm

U tom slučaju Z je posrednik koji prenosi učinak od X na Y. X sam po sebi ne izaziva Y i X ne izaziva Y kroz neku drugu varijablu (npr. toplinu). Tada kažemo da Z zaklanja (informacije o) X od Y, jer kada jednom saznamo vrijednost Z, vrijednost od X niti podiže niti smanjuje šanse za Y. Dakle, kontrola varijable Z spriječila bi da informacije o X dođu do Y i zato posrednika nikada ne smijemo kontrolirati.

Pretpostavimo da je varijabla Z kauzalno vezana s varijablama X i Y poput sudara:

X → Z ← Y

Jedan konkretni primjer je:

Talent → Slavna osoba ← Ljepota

U tom slučaju Z je mjesto sudara od X i Y. Varijable X i Y pridonose (pojavi od) Z, ali su u općoj populaciji jedna s drugom nepovezane. No, iako su X i Y nezavisne, kontrola varijable Z učinit će ih zavisnima (to da slavna osoba nije lijepa povećava šanse da je talentirana) i zato mjesto sudara nikada ne smijemo kontrolirati.

Općenito je od pomoći veze između X i Y zamišljati kao cijevi koje prenose informacije od starta X do cilja Y, imajući na umu da informacija teku u oba smjera, kauzalno i nekauzalno. Nekauzalni putovi su izvor lažne korelacije i njih treba blokirati, pazeći da pritom ne blokiramo neke kauzalne putove.

Preciznije, ako stražnjim putem nazovemo svaki put od X do Y koji počinje strelicom koja ide prema X, onda će lažna korelacija između X i Y biti spriječena blokiranjem svakog stražnjeg puta. Ako to učinimo kontroliranjem nekog skupa varijabli Z, moramo biti sigurni da nijedna od njih nije potomak od X na nekom kauzalnom putu; inače bismo mogli djelomično ili potpuno zatvoriti taj put.

Primjer 1.

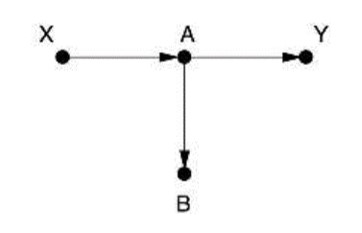
Nema strelica koje vode u X pa nema ni stražnjih putova i ništa  ne trebamo kontrolirati.

(Inače, B zadovoljava “klasičnu epidemiološku definiciju” zajedničkog uzroka pa mnogi istraživači smatraju da  B treba kontrolirati, ali to bi dovelo do pogrešnih rezultata.)

Primjer 2.

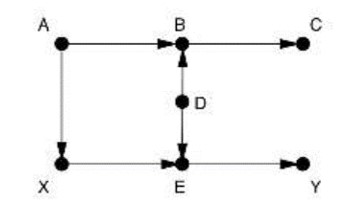
(A, B, C i D su pred-tretmani. Tretman je X.)

Postoji jedan stražnji put X←A→B←D→E←Y. Već ga blokira mjesto sudara B pa ništa ne trebamo kontrolirati. (Mnogi bi kontrolirali pred-tretman B ili C no to bi otvorilo nekauzalni put od X do Y i lažno bi ih koreliralo. U ovom slučaju mogli bismo taj put ponovno zatvoriti kontrolirajući A ili D. Ali to je nepotrebna komplikacija.)

Primjer 3.

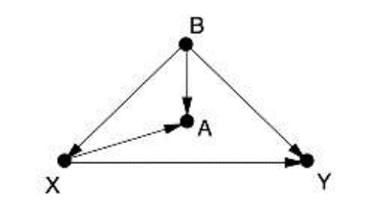
Postoji jedan stražnji put, X←B→Y, i on se može blokirati samo kontrolom varijable B. (Ako je varijabla B nemjerljiva, tada ne postoji način da se procijeni učinak od X na Y bez izvođenja randomiziranog kontroliranog eksperimenta; v. dolje. Većina statističara u ovoj bi situaciji kontrolirala A, kao zamjenu za nemjerljivu varijablu B, ali to samo djelomično eliminira lažnu korelaciju varijabli X i Y, a uvodi novu jer je A mjesto sudara koje ne smijemo kontrolirati.)

Primjer 4.

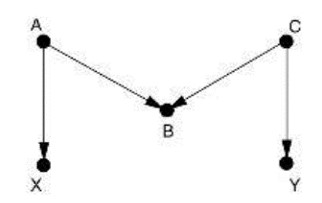
Postoji samo jedan stražnji put, a on je već blokiran mjestom sudara B. Dakle, ne trebamo ništa kontrolirati. (Statističari često B smatraju zajedničkim uzrokom, jer prolazi tradicionalni test za zajednički uzrok; povezanost varijable B i s X i s Y. Ali varijable X i Y nisu lažno korelirane ako ne kontroliramo varijablu B, a postaju lažno korelirane baš kada  kontroliramo B.)

Primjer 5.

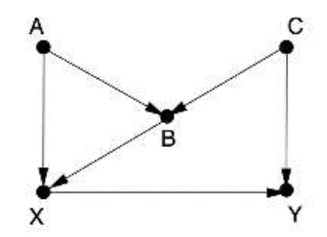
Primjeru 4 dodana je veza X←B koja stvara novi stražnju put X←B←C→Y. Ako zatvorimo taj put kontrolom varijable B, onda otvaramo put X←A→B←C→Y, jer kontroliramo mjesto sudara B. Da bismo ga zatvorili, moramo kontrolirati A ili C. No, jednostavnije je  kontrolirati samo C, koji zatvara put X←B←C→Y i ne utječe na drugi put.

Lažna korelacija i randomizirani eksperimenti

Varijable X i Y općenito definiramo kao lažno korelirane ako je Pr (Y | do (X)) ≠ Pr (Y | X). Na primjer, liječenje L i oporavak O lažno su korelirani jer je Pr (O | do (L)) ≠ Pr (O | L), tj.  vjerojatnost oporavka osobe kojoj dajem lijek različita je od vjerojatnosti oporavka osobe koju vidim da uzima lijek (v. gornji argument protiv Blytha). Do-operator briše sve strelice koje dolaze u X i na taj način sprječava da bilo koja informacija o X teče u nekauzalnom smjeru. To nam može objasniti zašto funkcioniraju randomizirani kontrolirani eksperimenti. Npr. u randomiziranom eksperimentu kojim želimo ispitati djeluje li fertilizator na prinos neke kulture imamo sljedeće uzročne veze:

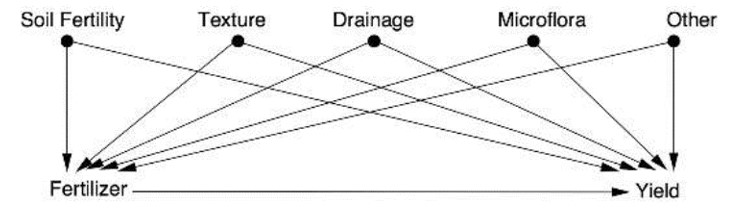
Umjesto da kontroliramo sve zajedničke uzroke, što je teško, a često i nemoguće (usp. primjer 3), situaciju simuliramo s randomiziranom distribucijom fertilizatora koja blokira sve zajedničke uzroke pa je njihova kontrola nepotrebna (a ionako je najčešće nemoguća).

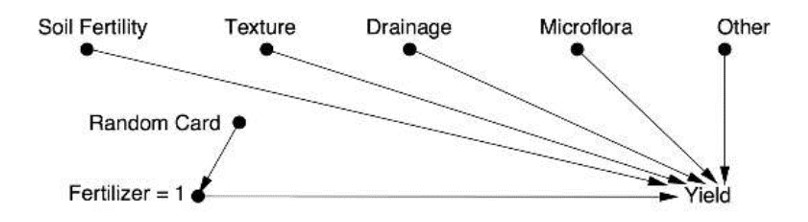
Često se nude i drugi, manje-više prihvatljivi, argumenti za randomizaciju eksperimenta, ali nijedan nije konkluzivan poput ovoga.

Nadam se da smo ovime dali osnovni uvid u kauzalnu revoluciju čiji je značaj ogroman za suvremenu empirijsku znanost.