Ključni problem rimskih brojeva. Razvoj prirodnih logaritama

Glavni problem sustava rimskih brojki je što nije imao nikakav sistematski način prikaza razlomaka, te je bio potpuno neprimjeren za precizne izračune u astronomiji, kao i za razvoj prirodnih logaritama, piše Zvonimir Šikić u reakciji na tekst Željka Ivankovića o knjizi Stephena Chrisomalisa o povijesti brojevnih sustava. Ističe kako su se još u antici za takve izračune koristili pozicijski brojevni sustavi.

• Naslovna fotografija: Seksagezimalni brojevni sustav kojeg su koristili Babilonci. (MacTutor, Sveučilište St. Andrews)

Željko Ivanković nedavno je na istom ovom portalu objavio članak Zašto je arapskim brojevima trebalo vise od pola milenija da zamijene rimske. U njemu je prikazao knjigu lingvističkog antropologa Stephena Chrisomalisa Reckonings: Numerals, Cognition and History .

Kako nas izvještava Ivanković:

“Veliki dio knjige Chrisomalis posvećuje opovrgavanju teze da su arapski brojevi prihvaćeni jer su efikasniji za manipulaciju nego rimski … Glavni je Chrisomalisov protuargument trostruk:

a) notacija brojeva ne služi računanju nego prikazu veličina;

b) jesu li arapski brojevi zaista efikasniji?;

c) ako su i efikasniji, to nije bio dovoljan razlog da se rimski brojevi generalno zamijene arapskima.

U vrijeme korištenja rimskim brojevima računalo se … na računaljkama (abacus/abakus). Chrisomalis navodi niz primjera u kojima se abacus pokazao efikasnijim … Notacija brojeva dakle ne služi prvenstveno računanju nego bilježenju veličina (rezultata). To je glavni zaključak lingvističkog antropologa Chrisomalisa o prirodi notacije brojeva. … Kako su onda rimski brojevi ipak zamijenjeni arapskim? Chrisomalis identificira više silnica … ključni je moment bio tiskarski stroj. … s vremenom su prvo u matematičkim knjigama ipak otiskivani arapski brojevi, a zatim i u komercijalne svrhe. Trgovci nisu nosili sobom abacus … [jer] nije bio praktičan koliko zbrajanje cijena na papiru.“

Što se tiče protuargumenata a), rimski sustav brojki nema nikakav sistematski način prikaza razlomaka i to ga definitivno čini lošim sustavom notacije brojeva čak i ako on „ne služi računanju nego prikazu veličina“, jer veličine nisu samo cjelobrojne.

Što se tiče protuargumenata b), opće je poznato da je abacus jednostavniji za elementarna računanja od „pismenih“ računanja u arapskom decimalnom sustavu. No, to je argument za abacus, a ne za rimske brojke.

Što se tiče protuargumenata c), ako efikasnost nije dovoljna, misli li Chrisomalis zaista da je dovoljna „činjenica“ da „nošenje abacusa nije bilo praktično koliko je to bilo zbrajanje cijena na papiru“. Nevjerojatna tvrdnja, jer je opće poznato, što potvrđuje japanska i mnoge druge tradicije, da je „nošenje abacusa“ neusporedivo praktičnije od „zbrajanja cijena na papiru“.

No, vratimo se protuargumentima a) i b). Zbrajanje i oduzimanje relativno se jednostavno izvodi i na abacusu i s arapskim decimalnim zapisima na papiru, no u oba slučaja množenje i dijeljenje znatno je složenije. Stoga je jedan od glavnih problema pri glomaznim računima, npr. u astronomiji, bio svesti množenje i dijeljenje na zbrajanje i oduzimanje. Kao što danas zna svaki srednjoškolac to su omogućavale logaritamske tablice, no gotovo nijedan ne zna kako su one konstruirane, a bojim se da to ne zna ni Chrisomalis. Da zna razumio bi zašto je rimska notacija popuno neprimjerena rješavanju tog važnog problema efikasnosti.

• Otkriće prirodnih logaritama

Mnoge iznenađuje činjenica da su prvi otkriveni logaritmi bili prirodni logaritmi. To su logaritmi s krajnje neobičnom bazom \( \small e \overset{\text{def}}{=} \lim_{x \to 0} (1 + x)^{\frac{1}{x}} = 2.71828 \)… . Još će se više iznenaditi kada saznaju da su oni prvi otkriveni jer se najlakše izračunavaju.

Čuđenje je opravdano ako se logaritamska tablica gleda kao računanje potencija, :

\(y\)	\(0\)	\(1/2\)	\(1\)	\(3/2\)	\(2\)	…
\(x = e^y\)	\(1\)	\(e^{\frac{1}{2}} = \sqrt{e}\)	\(e\)	\(e^{\frac{3}{2}} = e \sqrt{e}\)	\(e^2\)	…

Međutim, logaritmi su otkriveni na drugi način. U vrijeme njihova otkrića, razlomljene potencije b^q, gdje je q razlomak, još nisu ni poznate. Eksponenti su u to vrijeme bili isključivo prirodni brojevi 1, 2, 3, … . Zato ne može biti govora o funkciji e^y definiranoj čak ni za y-e koji su razlomci, a kamoli realni brojevi. Unatoč tome, prirodni logaritmi su uspješno definirani za svaki pozitivni realni broj x. Dodajmo i to da u vrijeme njihova otkrića, još nije bio otkriven infinitezimalni račun. Kako se to dogodilo?

Odavno je bilo poznato da tablice cjelobrojnih potencija, poput x = 2^Y, omogućavaju da se množenje (i dijeljenje) svede na zbrajanje (i oduzimanje).

Y	0	1	2	3	4	5	6	…
x = 2Y	1	2	4	8	16	32	64	…

Na primjer, želite li pomnožiti 4 · 16 (u x-retku) nađite njima pridružene brojeve (u Y-retku) i zbrojite ih, 2 + 4 = 6. Broj pridružen broju 6 (u x-retku) traženi je umnožak 64.

4 ⋅ 16 = 64 ⟺ 2 + 4 = 6

Dakle, dva broja x-retka množimo tako da zbrojimo njima pridružene brojeve Y-retka. Ti pridruženi Y-brojevi nazvani su logaritmima x-brojeva.

x₁ ⋅ x₂ = x₃ ⟺ Y₁ ⋅ Y₂ = Y₃

Paul Wittich, asistent Tycho Brahea, već je u 16. st. uveo metodu koja je množenja svodila na zbrajanja i oduzimanja uz pomoć trigonometrijskih tablica. Nazvao ju je prostefereza (  = zbrajanje i oduzimanje). Na primjer,

\(61620 \cdot 45318 = ?\)

\(0.61620 = \sin 38.039^\circ \quad 0.45318 = \sin 26.948^\circ\)

\(\sin\alpha \sin\beta = \frac{\displaystyle \cos(\alpha – \beta) – \cos(\alpha + \beta)}{\displaystyle 2}\)

\((\sin 38.039^\circ)(\sin 26.948^\circ) = \frac{\displaystyle \cos 11.091^\circ – \cos 64.987^\circ}{\displaystyle 2} =\)

\(\frac{\displaystyle 0.9813219765 – 0.42282294}{\displaystyle 2} = 0.279249516\)

\(61620 \cdot 45318 = 2792495160\)

No vratimo se tablici x = 2^Y. Njena praktična vrijednost zanemariva je zbog velikih „rupa“ među dostupnim x-ovima (za razliku od „gustih“ trigonometrijskih tablica). Pitanje je bilo kako dobiti finiju distribuciju x-ova. Na ovo su pitanje istovremeno i neovisno odgovorili Jost Bürgi i John Napier 1619.

Danas bismo sigurno odgovorili: finijom distribucijom Y-a, koju nam omogućavaju razlomljeni eksponenti (kao u prvoj od gornjih tablica). Ali to vodi k izračunavanju korijena, što odgovor čini računski bezvrijednim. Uostalom, već smo rekli da u vrijeme Bürgija i Napiera potencije s razlomljenim eksponentima nisu bile poznate, pa to nije mogao biti njihov odgovor. Oni su zadržali cjelobrojne eksponente i baš su time utrli put otkriću prirodnih logaritama.

Neka varijabla Y prima pozitivne cjelobrojne vrijednosti. Kako ćemo dobiti finiju distribuciju x-ova? “Najfiniju” distribuciju dobijemo kada kao bazu uzmemo b = 1. Tada se svi x-ovi stope u broj 1. Dakle, finu raspodjelu x-ova dobijemo za b = 1. Bürgi je odabrao bazu b = 1,0001, a Napier b = 0,9999999. Pokazat ćemo kako se prirodni logaritmi dobivaju Bürgijevim izborom.

Za Y = 1, 2, 3 … odgovarajuće x-ove dobijemo potenciranjem x = 1.0001^Y. Ali, da bi  izračunao, na primjer, 1.0001¹³¹  Bürgi nije množio 1.0001 sam sa sobom 131 put. Tko bi ikada došao do tablice logaritama na takav način? Naravno, svakome će pasti na pamet da koristi prethodno izračunatu vrijednost, na primjer 1.0001¹³⁰, za računanje sljedeće vrijednosti 1.0001¹³¹:

1.0001¹³¹ = (1.0001¹³⁰) · 1.0001.

To je nešto bolje. No Bürgi je znao još bolje. On je prethodno izračunati x koristio za izračunavanje prirasta sljedećem x-u. Dakle, za x = 1.0001^Y, on traži Δx  takav da bude

x + Δx = 1.0001^Y+1.

Dakle,

\( \Delta x = (x + \Delta x) – \Delta x = 1.0001^{Y+1} – 1.0001^Y = 1.0001^Y (1.0001 – 1) = \displaystyle \frac{x}{10000}\)

I kako se izračunava tablica logaritama? Za zadani x, pomaknete decimalnu točku četiri mjesta ulijevo i tako dobijete Δx koji dodate x-u. To je vrlo jednostavan algoritam.

Y	x	Δx
0	1	0.0001
1	1.0001	0.00010001
2	1.00020001	0.000100020001
3	1.000300030001	itd.

Nakon što je na ovaj jednostavni način napravljena tablica logaritama, uslijedio je korak prema finijoj distribuciji Y-a: oni su proporcionalno smanjeni za faktor \(\small \frac{1}{10000}\). Tako je izgrađena tablica koja povezuje x i y = \(\small \frac{Y}{10000}\).

y	X
0.0000	1
0.0001	1.0001
0.0002	1.00020001
0.0003	1.000300030001
0.0004	itd.

Nova tablica i dalje je logaritamska, tj. x₁ ⋅ x₂ = x₃ ⟺ y₁ ⋅ y₂ = y₃   . Njena prednost je što male promjene x-a odgovaraju malim promjenama y-a, i obrnuto. Stoga se odnos između x i y može lakše shvatiti kao kontinuirana funkcija.

Mislim da ne trebam posebno argumentirati da rimske brojke nikada ne bi dovele do logaritama i do opisanog postupka za njihovo izračunavanje. Osim toga one nikada ne bi dovele ni do trigonometrijskih tablica i  do postupka za njihovo izračunavanje, a njih je izračunao Ptolemej još u 2. stoljeću. Nije se koristio arapskim decimalnim zapisima (s bazom 10) nego seksagezimalnim (s bazom 60), ali princip je isti. Dakle, već u antici je zbog efikasnosti korišten pozicijski sustav. Ne-pozicijski sustavi poput rimskog ili grčkog alfabetskog sustava odbačeni su, kada je trebalo efikasno računati, već u antici.

No vratimo se logaritmima i pogledajmo o čemu se tu radi s današnjeg gledišta.

\(x = 1.0001^Y = 1.0001^{10000y} = \left( \left(1 + \displaystyle \frac{1}{10000} \right)^{10000} \right)^y \approx e^y\)

Sada je jasno otkuda „neobična“ definicija \( \small e \overset{\text{def}}{=} \lim_{x \to 0} (1 + x)^{\frac{1}{x}}\). Dodajmo da je gornja aproksimacija točna na tri decimale. Dakle, y-tablica je tablica logaritamske funkcije

y = log_b x za b ≈ e.

Dakle, Bürgijeva tablica daje približne vrijednosti prirodnih logaritama. Kada bismo za bazu u Y-tablici odabrali broj još bliži broju 1, a zatim prešli na novu tablicu dijeljenjem Y-a s odgovarajućim faktorom, dobili bismo još finiju raspodjelu x-ova i još bolju aproksimaciju prirodnih logaritama. No taj prijelaz na prirodne logaritme (koje Bürgi samo aproksimira) nije učinjen prijelazom na \(\small b = \left( 1 + \frac{1}{n} \right)^n\), za n → ∞.  Povijesni prijelaz na prirodne logaritme bio je geometrijski.

Razmotrimo još jednom Bürgijeve logaritme, tumačeći ih geometrijski.

Iz \(\small \Delta y = \frac{1}{10000}\)  i  \(\small \Delta x = \frac{x}{10000}\) slijedi \(\small \frac{\Delta y}{\Delta x} = \frac{1}{x}\). Prirast Δy (koji je uvijek jednak \(\small \frac{1}{10000}\)) može se geometrijski prikazati kao pravokutnik s visinom \(\small v = \frac{1}{x}\) i takvom bazom Δx  da površina tog pravokutnika bude \(\small \frac{\Delta x}{x} = \frac{1}{10000}\). Tada je zbroj svih prirasta Δy od 1 do x:

\(y = \sum_{1}^{x} \Delta y = \sum_{1}^{x} \frac{\Delta x}{x}\)

To je zbroj površina svih pravokutnika koji se protežu od 1 do x, čije se visine protežu do grafa funkcije \(\small v = \frac{1}{x}\) i čije su pojedinačne površine \(\small \frac{1}{10000}\).

­­

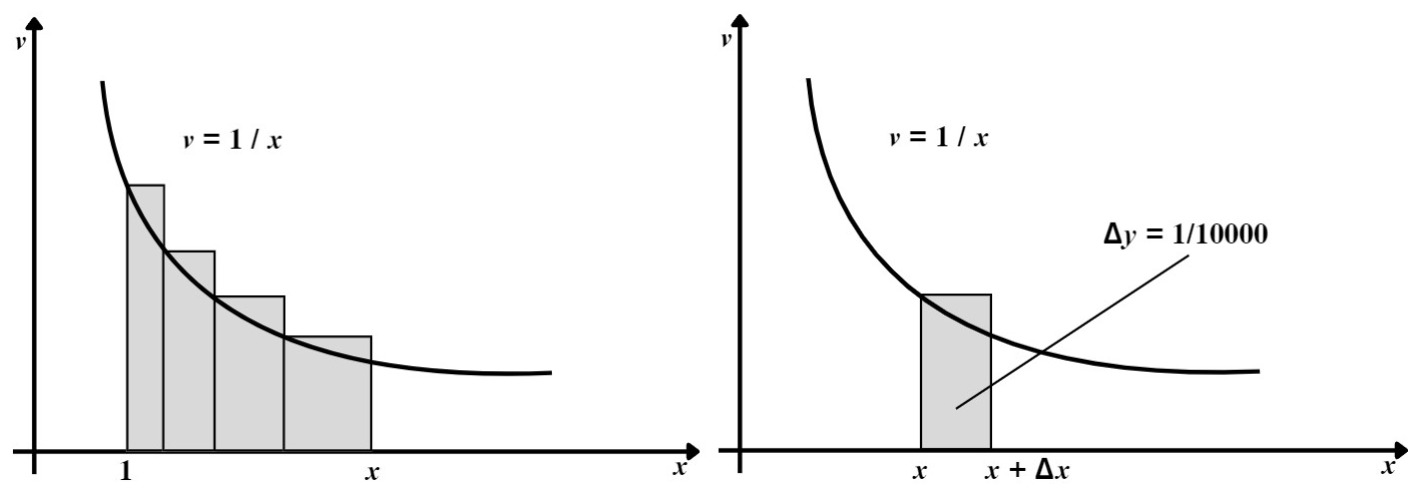
Ako je b sve bliži broju 1, onda pojedinačni pravokutnici imaju sve manje površine, a njihov je zbroj sve bliži površini ispod hiperbole. Dakle, geometrijski gledano, granični prijelaz na prirodne logaritme je prijelaz na površinu ispod hiperbole, tj.

\(\ln X = \displaystyle \int_1^X \frac{dx}{x}\)

Ovaj prijelaz napravio je Mercator u 1667.

• Decimalni razvoji

Ideju da se svakoj skalarnoj veličini kao njena mjera može pridružiti decimalni razvoj jasno je formulirao Stevin 1585. u knjizi De Thiende. Time su realni brojevi uvedeni kao univerzalna mjera veličina. Njenu su univerzalnost u 19. stoljeću dokazali Helmholtz (u osnovnoj ideji) i Hölder (matematički egzaktno). Na primjer

\(\pi = 3.14159\ldots \overset{\text{def}}{=} 3 + \frac{1}{10} + 4 \cdot \left( \frac{1}{10} \right)^2 + 1 \cdot \left( \frac{1}{10} \right)^3 + 5 \cdot \left( \frac{1}{10} \right)^4 + 9 \cdot \left( \frac{1}{10} \right)^5 + \cdots\)

Jasno je da sustav rimskih brojki (koji nema sistematski način prikaza razlomaka) ne može prikazati ni pojedine realne brojeve, na primjer π, a potpuno mu je nedostupna opća definicija realnog broja. Dodajmo da su analogne izmjere veličina u seksagezimalnom sustavu bile standardne u antici i arapskom srednjovjekovlju koje je sačuvalo antička znanja. Srednjovjekovna latinska matematika i znanost uopće doživjele su ogroman pad u odnosu na antiku pa su retardirale i u notaciji brojeva. Tek je renesansa (i dijelom kasni srednji vijek) najčešće preko Arapa, ponovno otkrila zaboravljena antička znanja. Tada je ponovno uvela i arapski pozicijski sustav zapisivanja brojeva.

Uskoro je procvjetala Europska matematika i znanost. Na primjer, po uzoru na decimalne razvoje realnih brojeva (poput gornjeg razvoja od π) Newton će razviti sve elementarne funkcije. Na primjer (uz 3! = 2 · 3, 4! = 2 · 3 · 4 itd.).

\(e^x = 1 + x + \frac{1}{2} \cdot x^2 + \frac{1}{3!} \cdot x^3 + \frac{1}{4!} \cdot x^4 + \frac{1}{5!} \cdot x^5 + \cdots\)

\(\cos x = 1 – \frac{1}{2} \cdot x^2 + \frac{1}{4!} \cdot x^4 – \frac{1}{6!} \cdot x^6 + \frac{1}{8!} \cdot x^8 – \cdots\)

\(\sin x = x – \frac{1}{3!} \cdot x^3 + \frac{1}{5!} \cdot x^5 – \frac{1}{7!} \cdot x^7 + \frac{1}{9!} \cdot x^9 + \cdots\)

To će mu omogućiti da integrira sve elementarne funkcije koristeći se dobro poznatim integralima

\(\int x^n \, dx = \frac{x^{n+1}}{n+1}\)

Ovakve dalekosežne ideje nisu mogle proizaći iz rimske notacije za brojeve.

• Dodatak o kompleksnim logaritmima

I na kraju, samo za one koji znaju nešto više matematike, nudimo i objašnjenje logaritma kompleksnoga broja. Ono prirodno slijedi iz Mercatorove definicije \(\small \ln X = \int_1^X \frac{dx}{x}\), a za nju smo već vidjeli kako prirodno proizlazi iz računanja logaritama u arapskoj decimalnoj notaciji.

Polazeći od Mercatorove definicije prirodnog logaritma, koja je bila standardna sve do polovice 20. stoljeća, prirodni logaritam u kompleksnoj ravnini \(\mathbb{C}\) definiran je s

\(\ln Z = \int_1^Z \frac{dz}{z}\)

U \(\mathbb{R}\) postoji samo jedan put od 1 do svakog Z > 0  i ne postoji nijedan put od 1 do Z < 0 (jer funkcija \(\small \frac{1}{z}\)  nije definirana u 0). Zato je realna funkcija ln definirana na \(\mathbb{R}^+\).

U kompleksnoj ravnini \(\mathbb{C}\) postoji mnogo puteva od 1 do svakog Z ≠ 0. Zato je ln višeznačna kompleksna funkcija definirana na \(\mathbb{C} \setminus \{0\}\).

­­

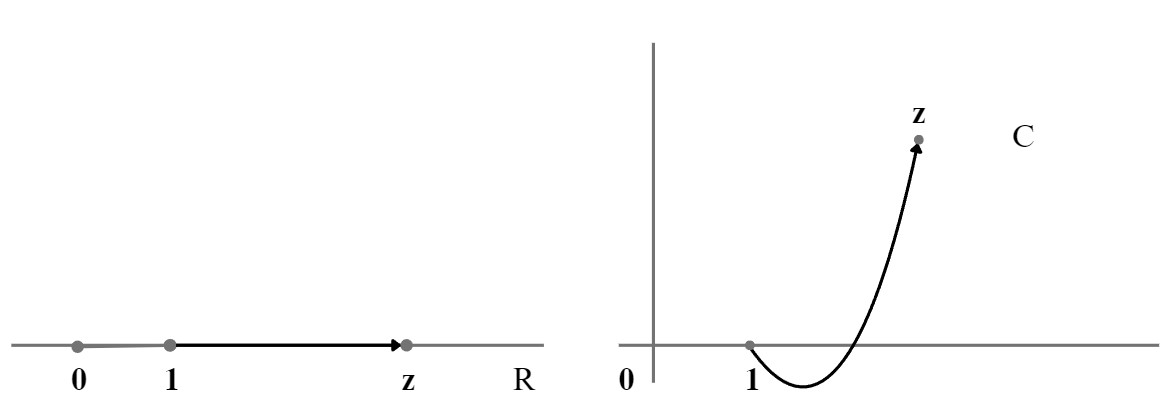
­Izračun vrijednosti lnZ  je jednostavan.

­­

Označimo trigonometrijski oblik broja z = r(cosφ + isinφ) s [r,φ]. Tada je (vidi sliku)

\(dz = [dr, \varphi] + [r d\varphi, \varphi + \frac{\pi}{2}] = [dr, \varphi] + i [r d\varphi, \varphi]\)

\(\displaystyle \frac{dz}{z} = \frac{[dr, \varphi]}{[r, \varphi]} + i \frac{[r d\varphi, \varphi]}{(r, \varphi)} = \frac{dr}{r} + i d\varphi\)

\(\ln Z = \int_1^Z \frac{dz}{z} = \int_1^R \frac{dr}{r} + i \int_0^\Phi d\varphi = \ln R + i(\Phi + 2k\pi)\)

gdje je k broj okreta oko 0, na putu od 1 do Z. Dakle,

\(\ln[R, \Phi] = \ln R + i(\Phi + 2k\pi)\).

Ako je ln[R,Φ] = X + iY onda je R = e^x i Φ = Y – 2kπ pa odmah slijedi

\(e^{X + iY} = [R, \Phi] = e^X (\cos Y + i \sin Y)\).

Dakle, prirodna logaritamska i eksponencijalna funkcija imaju sljedeće vrijednosti:

\(\ln \left( r (\cos \varphi + i \sin \varphi) \right) = \ln r + i (\varphi + 2k\pi)\),

\(e^{x + iy} = e^x (\cos y + i \sin y)\).